Уравнения состояния для расчета температур ударно-волнового сжатия молекулярных кристаллов
Автор: Ковалев Юрий Михайлович, Шестаков Михаил Александрович
Рубрика: Физика
Статья в выпуске: 2 т.16, 2024 года.
Бесплатный доступ
Проведен анализ уравнений состояния энергетических материалов, которые являются молекулярными кристаллами, с целью определения оптимального вида уравнения состояния, позволяющего определять температуры ударно-волнового сжатия данных материалов. Анализ холодной составляющей давления показал, что ее форма позволяет с высокой точностью воспроизводить известные экспериментальные данные для триаминотринитробензола (ТАТБ) и пентаэритриттетранитрата (ТЭНа). В силу того, что для энергетических материалов при ударно-волновом сжатии происходит инициирование детонации построить ударную адиабату в широком диапазоне давлений не представляется возможным, в представленной работе был апробирован алгоритм построения ударных адиабат по экспериментальным данным изотермического сжатия ТАТБ и ТЭНа. Сравнение экспериментальных и расчетных ударных адиабат для ТЭНа показало их совпадение с точностью погрешности эксперимента. В работе на примере ТАТБ и ТЭНа предлагается подход к определению температур ударно-волнового сжатия энергетических материалов путем расчета распространения в них стационарной ударной волны. Предлагаемый подход позволяет построить ударные адиабаты энергетических материалов и провести анализ влияния различных выражений для описания зависимости теплоемкости при постоянном объеме от температуры на величину температуры ударно-волнового сжатия энергетических материалов.
Ударное сжатие, ударная адиабата, изотермическое сжатие, температура
Короткий адрес: https://sciup.org/147242986
IDR: 147242986 | УДК: 662.237.5, | DOI: 10.14529/mmph240209
Текст научной статьи Уравнения состояния для расчета температур ударно-волнового сжатия молекулярных кристаллов
Исследования закономерностей энерговыделения в конденсированных энергетических веществах (ЭВ) под действием ударных волн проводятся с целью выяснения механизмов инициирования и развития реакции взрывчатого превращения, кинетика которого тесно связана с температурой ударно-волнового разогрева, получения информации, необходимой для прогнозирования ударно-волновых и детонационных процессов [1].
В настоящее время для получения детальной информации при анализе экспериментальных данных все чаще применяется подход, связанный с математическим моделированием механизмов инициирования и развития реакции взрывчатого превращения. Для получения достоверной информации в результате математического моделирования и проведения расчетов требуются надежные уравнения состояния ЭВ. Однако для ЭВ построить надежную ударную адиабату очень часто не представляется возможным. Это связано с возможностью развития в ЭВ детонационных процессов. Поэтому целью данного исследования является построение уравнений состояния кристаллических ЭВ ТАТБ и ТЭНа, позволяющих определять ударно-волновой разогрев кристаллических ТАТБ и ТЭНа.
Метод расчета температур ударного сжатия
Для расчета температур ударного сжатия рассмотрим распространение стационарной ударной в ТАТБ и ТЭНе. Система уравнений газовой динамики, описывающая распространение ударной волны, в лагранжевых переменных h, t имеет следующий вид:
ev ) 1 (du)
d t ) p 0 yd h )
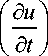
+ -1 V-P- 1 = 0;
Р 0 Ve hh )
(a E У p [a u L о; (3)
V d
t
)
p
0
где ρ 0 является начальной плотностью, u – скорость частиц, V – удельный объем, p – давление в направлении распространения и E – внутренняя энергия. Данная система законов сохранения замыкается уравнениями состояния, которые имеют следующий вид [2, 3]:
P = MRTYD (V) d(Xd ) + Px, Px = Pc + Pm + 3 ^^ ^^ / y,(4)
V8
Pc= -^U7,PM= -^UT, E = UC + UM + E0 + Et ’(5)
о Vо V где M – количество деформационных колебаний, метод определения описан в работе [4], R – универсальная газовая постоянная, поделенная на молекулярную массу ЭВ, T - температура, yd
- коэффициент Грюнайзена, D(xD) - функция Дебая, xD - безразмерная характеристическая температура Дебая, UC – межмолекулярная (упругая) составляющая внутренней энергии, которая определяет энергию не валентных взаимодействий атомов между молекулами, UM – внутримолекулярная составляющая внутренней энергии, определяющая энергию взаимодействия атомов внутри молекулы, E – энергия нулевых колебаний, E – тепловая составляющая внут- ренней энергии, Px – «холодная» составляющая давления. Выражения для «холодных» состав- ляющих, входящих в уравнения состояния (4) и (5), были определены в работах [2, 3] и имеют следующий вид:
PC = 3KT0 (x-(n+4/3) - x-n+1)),(6)
3KTо f Г„-(П+4/3) _ -(n+1)Ъ _ 3KT0 1 -(n+1/3) _!-
I x- x- 1/tx' x-x-
Р0 JL r Р0 L(n+1/3)
где KT 0 = c T p 0 - изотермический модуль объемного сжатия, cT - изотермическая скорость звука, р 0 - начальная плотность, x = p 0 / p . Часть холодного давления P M является постоянной величиной и определяется из условия равенства давления величине P при нормальных условиях. Для апробации уравнений (6) и (7) были проведены расчеты значений изотермического сжатия xрасч по известным экспериментальным значениям давления. Результаты расчетов для ТАТБ [4] и ТЭНа [5] представлены в табл. 1 и 2 соответственно.
Таблица 1
|
№ |
X эксп . |
P 3KCn . , ГПа |
X расч . |
Р расч . - кг/м 3 |
|
1 |
0,9581–0,9635 |
0,56 |
0,9683 |
2,0004 |
|
2 |
0,9466–0,9530 |
0,85 |
0,9551 |
2,0281 |
|
3 |
0,9355–0,9439 |
1,20 |
0,9410 |
2,0584 |
|
4 |
0,9227–0,9313 |
1,66 |
0,9249 |
2,0943 |
|
5 |
0,9104–0,9192 |
1,95 |
0,9158 |
2,1151 |
|
6 |
0,9003–0,9105 |
2,42 |
0,9026 |
2,1460 |
|
7 |
0,8776–0,8892 |
3,29 |
0,8818 |
2,1966 |
|
8 |
0,8509–0,8651 |
4,95 |
0,8506 |
2,2772 |
|
9 |
0,8038–0,8230 |
8,18 |
0,8077 |
2,3982 |
|
10 |
0,7946–0,8144 |
8,53 |
0,8039 |
2,4095 |
|
11 |
0,7833–0,8053 |
9,53 |
0,7938 |
2,4402 |
|
12 |
0,7749–0,7989 |
10,17 |
0,7879 |
2,4584 |
|
13 |
0,7581–0,7833 |
11,64 |
0,7753 |
2,4984 |
|
14 |
0,7427–0,7731 |
13,22 |
0,7633 |
2,5377 |
Физика
Таблица 2
|
№ |
X эксп ■ |
P 3Kcn ■ , ГПа |
X расч ■ |
Р расч ■ - кг/м 3 |
|
1 |
0,9414–0,9460 |
0,68 |
0,9466 |
1,8741 |
|
2 |
0,9150–0,9186 |
1,28 |
0,9153 |
1,9382 |
|
3 |
0,8729–0,8797 |
2,25 |
0,8789 |
2,0184 |
|
4 |
0,8565–0,8623 |
2,90 |
0,8601 |
2,0626 |
|
5 |
0,8389–0,8431 |
3,65 |
0,8420 |
2,1069 |
|
6 |
0,8164–0,8186 |
4,98 |
0,8161 |
2,1738 |
|
7 |
0,8149–0,8177 |
5,00 |
0,8157 |
2,1749 |
|
8 |
0,8021–0,8063 |
5,86 |
0,8019 |
2,2122 |
|
9 |
0,7786–0,7850 |
7,45 |
0,7805 |
2,2729 |
|
10 |
0,7701–0,7759 |
8,11 |
0,7728 |
2,2955 |
|
11 |
0,7647–0,7695 |
8,40 |
0,7696 |
2,3051 |
|
12 |
0,7586–0,7632 |
9,16 |
0,7617 |
2,3290 |
|
13 |
0,7502–0,7548 |
10,12 |
0,7525 |
2,3575 |
|
14 |
0,7481–0,7529 |
10,45 |
0,7495 |
2,3669 |
При определении величины x расч в расчетах давления по уравнению (6) были использованы значения K T 0 = 15,14 ГПа для ТАТБ и K T 0 =9,62 ГПа для ТЭНа и показатели степени n = 3,177 для ТАТБ и n = 3,432 для ТЭНа [2, 3]. Анализ табл. 1 и 2 показывает, что значения x расч попадает в погрешность эксперимента, представленную во втором столбце.
В силу того, что для большинства энергетических материалов не удается определить экспериментальную ударную адиабату, в работах [3] и [6] был предложен алгоритм пересчета экспериментальных данных по изотермическому сжатию на ударную адиабату. В результате была получена формула, которая имеет следующий вид:
X aPT (x) + J PT (x) dx + b (1 - x)
P S( V ) = ryy , a = cv p o /( а К т о ), b = a K o T o ■ (8)
a - (1 - x )/2
Здесь P T ( x ), Ps ( x ) - экспериментальные значения давления при изотермическом сжатии и ударно-волновом сжатии соответственно. Как было показано в работе [3] экспериментальные данные, представленные в работе [7], аппроксимируются зависимостью
D = 2680 + 1,89 и , (9)
что позволило определить давление в ударной волне для ТЭНа, представленное в табл. 3.
Таблица 3
|
№ |
x |
PT ( x ), ГПа (эксп.) |
PS ( x ), ГПа (эксп.) |
Ps ( x ), ГПа |
|
1 |
0,9466 |
0,68 |
0,73 |
0,72 |
|
2 |
0,9153 |
1,28 |
1,53 |
1,36 |
|
3 |
0,8789 |
2,25 |
2,59 |
2,39 |
|
4 |
0,8601 |
2,90 |
3,29 |
3,08 |
|
5 |
0,8420 |
3,65 |
4,09 |
3,89 |
|
6 |
0,8161 |
4,98 |
5,51 |
5,32 |
|
7 |
0,8157 |
5,00 |
5,53 |
5,35 |
|
8 |
0,8019 |
5,86 |
6,45 |
6,29 |
|
9 |
0,7805 |
7,45 |
8,25 |
8,04 |
|
10 |
0,7728 |
8,11 |
8,76 |
8,77 |
|
11 |
0,7696 |
8,40 |
9,21 |
9,10 |
|
12 |
0,7617 |
9,16 |
9,93 |
9,95 |
|
13 |
0,7525 |
10,12 |
11,01 |
11,03 |
|
14 |
0,7495 |
10,45 |
11,39 |
11,40 |
Результаты, представленные в четвертом и пятом столбцах табл.3, показывают, что значения давления в ударной волне, распространяющейся в ТЭНе, рассчитанные по формулам (8) и (9), совпадают с точностью до 1–2 %. В работе [3] было показано, что давление ударно-волнового сжатия ТЭНа, полученное по алгоритму пересчета, предложенному в работе [6], ниже экспериментальных значений давления во фронте ударной волны [7].
Значения давления во фронте ударной волны ТАТБ, рассчитанные по алгоритму пересчета [3] представлены в табл. 4.
Таблица 4
|
№ |
x |
PT ( x ), ГПа (эксп.) |
Ps ( x ), ГПа |
|
1 |
0,9683 |
0,56 |
0,57 |
|
2 |
0,9551 |
0,85 |
0,87 |
|
3 |
0,9410 |
1,20 |
1,23 |
|
4 |
0,9249 |
1,66 |
1,70 |
|
5 |
0,9158 |
1,95 |
2,00 |
|
6 |
0,9026 |
2,42 |
2,48 |
|
7 |
0,8818 |
3,29 |
3,38 |
|
8 |
0,8506 |
4,95 |
5,10 |
|
9 |
0,8077 |
8,18 |
8,48 |
|
10 |
0,8039 |
8,53 |
8,85 |
|
11 |
0,7938 |
9,53 |
9,91 |
|
12 |
0,7879 |
10,17 |
10,59 |
|
13 |
0,7753 |
11,64 |
12,15 |
|
14 |
0,7633 |
13,22 |
13,85 |
Уравнение внутренней энергии (3) в результате простых преобразований можно представить следующим образом:
Су — + ( P + P + ( 6UC + U M + E о) )г)— = 0, PT = a KTOT + P ,
V 01 T x e v dt T 00
или же
Cv , ' Pt ^7 = 0,(10)
dt где Су - теплоемкость при постоянном объеме, a - коэффициент объемного расширения. Значения давлений ударно-волнового сжатия PS(x) из табл. 3 и 4 определяются граничными условиями для системы дифференциальных уравнений (1), (2), (10).
Система уравнений (1), (2), (10) решалась методом Неймана–Рихтмайера. При проведении расчетов для теплоемкости при постоянном объеме были использованы два выражения – через частоты нормальных колебаний [8]:
C v = MRD c ( Xd ) + R У -^ -^p^ . (11)
i = m +i (exp( x ) - 1)
и через аппраксимационную зависимость [8, 9]:
C v I Cvh = 1 - (1 - C V / Ch )exp[ - ( T - T )/ T ], (12)
где x i - безразмерная характеристическая температура внутримолекулярных колебаний, Dc ( xD ) - функция теплоемкости Дебая, C VH = 3 NR , N - количество атомов в молекуле, C V — значение теплоемкости при постоянном объеме при начальной температуре, Tc – параметр, определенный в работе [9], для ряда органических соединений.
Контроль выполнения условий Гюгонио во фронте ударной волны осуществлялся путем сравнения значений изменения внутренней энергии, полученной в расчетах на ударной адиабате:
К Е sh = 0,5 P (1 - x )/ р , и уравнениями состояния:
К Е = 3 К т 0 f ( x ' n + 1/3) - 1) - 1 ( x - n - 1)
/ P 0 - ( а К т 0 T 0 - P 0 )(1 - x ) / P 0 + К Е т, ,
^ ( n + 1/3) n
К Е т 1 = C^(T - T ,) + Tc ( Cvh - C V )(exp( - ( T - T)/T ) - 1),
Физика
-
3 N X 3 N x °
b E T 2 = MR(T - T ° ) + RT У -i - ET ° , ET ° = RT ° ^ -i ° , x ° = 0JT ° .
i = M +1 eXP( x i ) 1 i = M +1 exP( x i ) - 1
Результаты расчетов температур ударно-волнового сжатия ТЭНа и ТАТБ для разных выражений теплоемкости при постоянном давлении приведены в табл. 5 и 6 соответственно.
Таблица 5
|
P S , ГПа |
u, км/c |
p - |
T 1 , К |
T 2 , К |
|
0,725 |
147,3 |
0,9468 |
313,2 |
313,5 |
|
1,360 |
254,3 |
0,9155 |
328,0 |
328,4 |
|
2,388 |
403,3 |
0,8790 |
351,6 |
352,4 |
|
3,081 |
492,5 |
0,8601 |
368,4 |
369,4 |
|
3,885 |
588,0 |
0,8419 |
388,9 |
390,1 |
|
5,325 |
743,3 |
0,8156 |
428,0 |
429,7 |
|
5,346 |
745,4 |
0,8153 |
428,6 |
430,3 |
|
6,286 |
838,3 |
0,8013 |
455,5 |
457,6 |
|
7,563 |
956,7 |
0,7850 |
493,7 |
496,2 |
|
8,039 |
998,8 |
0,7795 |
508,2 |
510,9 |
|
8,773 |
1061,7 |
0,7716 |
530,8 |
533,8 |
|
9,097 |
1088,9 |
0,7683 |
541,0 |
544,0 |
|
9,947 |
1158,5 |
0,7602 |
567,9 |
571,2 |
|
11,028 |
1243,6 |
0,7507 |
602,7 |
606,2 |
|
11,400 |
1272,1 |
0,7477 |
614,8 |
618,4 |
Таблица 6
|
P S , ГПа |
u, км/c |
x |
T 1 , К |
T T 2 , К |
|
0,574 |
96,8 |
0,9684 |
301,4 |
301,4 |
|
0,871 |
142,1 |
0,9551 |
305,3 |
305,3 |
|
1,229 |
193,5 |
0,9410 |
309,9 |
310,0 |
|
1,700 |
256,7 |
0,9249 |
316,0 |
316,2 |
|
1,997 |
294,5 |
0,9159 |
320,1 |
320,3 |
|
2,480 |
353,0 |
0,9027 |
326,9 |
327,2 |
|
3,376 |
453,9 |
0,8818 |
340,8 |
341,3 |
|
5,095 |
627,1 |
0,8505 |
371,4 |
372,6 |
|
8,478 |
918,4 |
0,8073 |
443,2 |
446,4 |
|
8,847 |
947,3 |
0,8035 |
451,7 |
455,1 |
|
9,906 |
1028,1 |
0,7934 |
476,7 |
480,8 |
|
10,587 |
1078,3 |
0,7873 |
493,1 |
497,8 |
|
12,155 |
1189,4 |
0,7746 |
531,9 |
537,7 |
|
13,849 |
1303,5 |
0,7624 |
575,1 |
582,1 |
Результаты, представленные в табл. 5 и 6, показывают, что различие между температурами ударно-волнового сжатия ТЭНа и ТАТБ, рассчитанными по различным выражениям для теплоемкости, составляет не более четырех градусов. Поэтому при расчетах температур ударноволнового сжатия энергетических материалов целесообразно использовать выражение (12), не привлекая сложные квантово-химические методы для расчета внутримолекулярных частот нормальных колебаний, входящих в выражение для теплоемкости при постоянном объеме (11).
Список литературы Уравнения состояния для расчета температур ударно-волнового сжатия молекулярных кристаллов
- Ударно-волновые явления в конденсированных средах / Г.И. Канель, С.В. Разоренов, А.В. Уткин, В.Е. Фортов. - Москва: Янус-К, 1996. - 407 с.
- Ковалев, Ю.М. Уравнения состояния для описания изотермического сжатия некоторых молекулярных кристаллов нитросоединений / Ю.М. Ковалев // Инженерно-физический журнал. - 2020. - Т. 93, № 1. - С. 229-239.
- Ковалев, Ю.М. Уравнения состояния для расчета давлений ударно-волнового сжатия пентаэритриттетранитрата (ТЭНа) / Ю.М. Ковалев, Е.В. Помыкалов // Инженерно-физический журнал. - 2023. - Т. 96, № 4. - С. 1053-1061.
- Hydrostatic Compression Curve for Triamino - Trinitrobenzene Determined to 13,0 GPa with Powder X- Ray Diffraction / L.L. Stevens, N. Velisavljevic , D.E. Hooks, D.M. Dattelbaum // Propellants, Explos. Pyrotech. - 2008 - Vol. 33, no. 4. - P. 286-295.
- Cady, H.H.The Crystal Structure of 1,3,5 - triamino - 2,4,6 - trinitrobenzene / H.H Cady, A.C. Larson // Acta Cyst. - 1965. - Vol. 18. - P. 485-496.
- Olinger, B. The isothermal linear and volume compression of pentaerythritol tetranitrate (PETN) t 10 GPa (100 kbar) and the calculated shock compression / B. Olinger, P.M. Halleck, H.H. Cady // J. Chem. Phys. - 1975. - Vol. 62, Iss. 11. - P. 4480 - 4483.
- Marsh, S.P. Lasl Shock Hungoniot Data (Los Alamos Scientific Laboratory Series on Dynamic Material Properties) / S.P. Marsh. - University of California Press, 1980, Vol. 5.
- Ковалев, Ю.М. Определение температурной зависимости теплоемкости для некоторых молекулярных кристаллов нитросоединений / Ю.М. Ковалев, В.Ф. Куропатенко // Инженерно-физический журнал. - 2018. - Т. 91, № 2. - С. 297-306.
- Щетинин, В.Г. Расчет теплоемкости органических веществ в ударных и детонационных волнах / В.Г. Щетинин // Химическая физика. - 1999. - Т. 18, № 5 - С. 90-95.


