Уравнения в гидродинамике в неинерциальной системе отсчета (геодезический подход)

Введение . Преимуществом задач гидродинамики является наглядность траекторий движения жидкости. В данной статье рассматривается движение закрученных потоков. Характерный пример такого движения – истечение жидкости с образованием воронки (рис. 1).

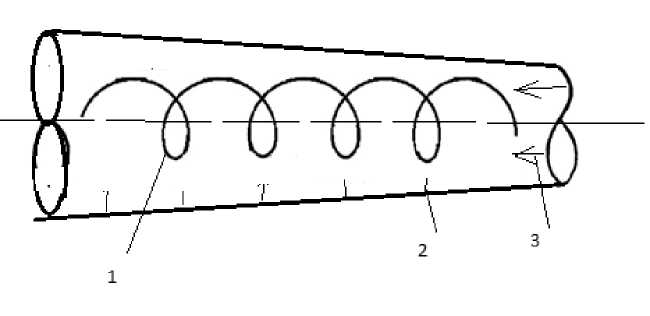
Рис. 1. Траектория частицы жидкости в закрученном потоке: 1 – закрученный поток; 2 – реперные точки; 3 – сила разряжения вихря

Уравнения гидродинамики базируются на втором законе И. Ньютона. Прежде чем к ним перейти, остановимся на понятии неинерциальной системы отсчета с точки зрения геодезии. При этом в основу представления о пространстве положим формулировку Э. Маха: «Вместо того, чтобы относить движущееся тело к пространству (к какой-нибудь системе координат), мы будем теперь прямо рассматривать его отношение к телам мирового пространства, которыми эта система координат может быть определена» [1, с. 198 ].

В соответствии с принципом относительности Маха и геодезическим подходом определим пространство как набор материальных тел (пунктов геодезической сети) с отношениями

(связями, расстояниями) между ними. При этом система отсчета – выделенная для определения координат часть пространства.

Время (внутреннее геодезическое) определим как изменение состояния пространства (системы отсчета). Состояние пространства характеризует момент внутреннего времени.

Под системой координат условимся понимать систему отсчета с заданным алгоритмом получения координат. Под инерциальной системой отсчета понимаем набор геодезических пунктов (реперные точки в потоке жидкости), изменение расстояний (рис. 2) между которыми при повторных измерениях на ограниченном интервале эталонного (астрономического) времени не обнаружено.

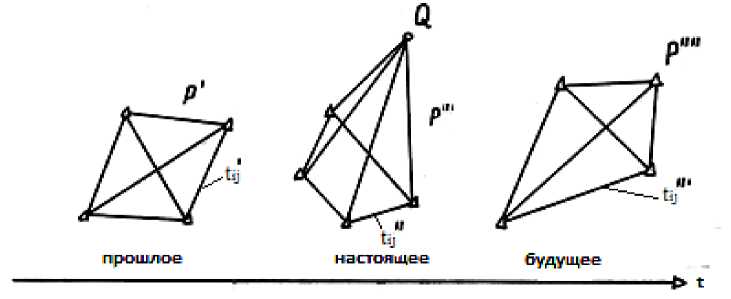
Рис. 2. Неинерциальная система отсчета

Соответственно, неинерциальной системой отсчета назовем набор материальных тел с изменяющимися от эпохи к эпохе (при повторных измерениях) взаимными расстояниями.

Для алгебраического представления принципа относительности Э. Маха по аналогии с комплексным видом интервала Г. Минковского

• [2]    введем кинематический интервал (интервал Э. Маха)

M= ⃗ R⃗ +і , (1) где ^⃗ R^⃗ – классический радиус-вектор; Т – матрица взаимных расстоя ни й между элементами системы отсчета; і=√-1 (см. рис.2)

Для упрощения выкладок преобразуем матрицу Т в вектор ^⃗ Т^⃗ . Для этого введем нормы матриц прошлого Т пр , настоящего Т наст и буду-щего Т буд и на их основании составим вектор ^⃗ Т^{⃗ ⃗⃗⃗⃗⃗⃗⃗}Т^⃗⃗ = ‖t‖_пр⃗е⃗_х + ‖t‖_наст⃗е⃗_у + ‖t‖_буд⃗е⃗ z .     (2)

Тогда формулу (1) можно переписать в виде ^⃗M^⃗ = ^⃗ R^⃗   + і ^⃗ Т^⃗ .           (3)

Прежде чем перейти к уравнениям гидродинамики в неинерциальной системе отсчета (в потоке с кручением) на основе кинематического интервала (3), сформулируем два неклассиче- ских кинематических принципа.

• 1.    Геодезический принцип эквивалентности

• 2.    Принцип инерции

(принцип Панина В.М.)

Изменение координат т. Q за счет изменения взаимных расстояний между элементами системы отсчета эквивалентно перемещению т. Q d⃗M⃗ = d⃗R⃗   + іτԁ⃗Т⃗,         (4)

где τ – эквивалентный коэффициент.

Инерция тела Q определяется изменением взаимного положения тел системы отсчета

(принадлежащей закрученому потоку).

Отсюда d2 ⃗⃗⃗⃗ d2 ⃗⃗ PQ , . d2 ⃗⃗ --- = ----- + IT---.

dt² dt² τ .

Следуя второму закону И. Ньютона и ципам (1), (2), запишем

_ d221 — m    =F + іF >

(5) прин-

где F_H – движущая сила И. Ньютона (в гидродинамике это сила тяжести); – полные производные; m_a – масса частицы Q; Ftr – трансверсальная сила (впервые заявленная в переписке Ньютона И. и Бентли Р.) [3]. Примем, что

⃗F⃗ tr = τ∇ ⨯× ⃗F⃗in , (7) где ⃗F⃗ – сила инерции, возникающая в неинерци- альной системе отсчета (см 1-й и 2-й принципы).

По аналогии с уравнениями электромагнитного поля в неподвижной среде [4] запишем си- стему уравнений гидродинамики для закручено- го потока

⃗ ⃗

{ 1

= F + іτ∇ ×⨯ ⃗F⃗

- х^ ⃗⃗ in = ∇ ×⨯ ⃗V⃗  , dt

где V= – полная скорость (см. 1-й принцип); 1 – калибровочный коэффициент.

Второе уравнение в системе (8) получено исходя из экспериментальных данных [5].

Возьмем ротор от левой и правой частей первого уравнения в системе (8) и подставим второе уравнение (8) в первое. Тогда, учитывая, что 7 ∙ ⃗⃗ = 0, а 7∙ Ph = 0, получим уравнение для определения ⃗F⃗ d2⃗⃗

• ^- It d = -іτΔ^⃗F^⃗ in .         (9)

Распределение полной скорости ^⃗⃗ после решения (9) можно получить из второго уравнения (8).

Выводы . Полученные уравнения позволяют моделировать вихревые течения жидкости и газа, например, в трубопроводном транспорте.