Уравнения вида F\x, g (х)) = F\x h(x)) и нестандартные методы решения

Современное состояние математической науки характеризуется, с одной стороны, наличием в ней разветвленной системы различных разделов и теорий, а с другой — укреплением ее единства. Этому Способствует введение общих понятий, которое приводит к систематизации и объединению большого числа разнообразных результатов, исчезновению резко очерченных границ между отдельными областями этой науки.

К основным содержательно-методическим линиям школьного курса математики относятся функциональная линия и линия уравнений и неравенств, фундаментальными понятиями которых являются понятия функции и уравнения. Анализ школьных учебников и пособий по математике показал, что понятия функции и уравнения связаны между собой формально (на уровне функционального определения уравне ния) либо эта связь односторонняя (уравнения используются при исследовании функций, а свойства функций не применяются при решении уравнений; задачи, основанные на использовании свойств функций, считаются трудными, а приемы и методы их решения — нестандартными).

Чтобы устранить эту ситуацию, необходимо было найти соответствующий теоретический и заданный материал, который не выходил бы за рамки школьной программы по математике и содействовал овладению учащимися основным курсом на более высоком уровне. Нами был выделен класс уравнений вида /ХуСг)) = = /(ЛСх)), который включил в себя традиционные школьные уравнения и уравнения, решаемые функциональными методами. Рассмотрение этого класса уравнений на школьных факультативных занятиях по-

зволило систематизировать знания учащихся, усовершенствовать процесс обучения математике на основе органичного сближения понятий функции и уравнения.

В процессе дальнейшего исследования оказалось возможным связать между собой понятия уравнения с одним неизвестным и функции двух переменных благодаря использованию мало применявшихся ранее понятий (монотонная по переменной функция, четная по переменной функция, периодическая по переменной функция), обобщающих известные понятия монотонности, четности, периодичности. Это помогло разработать функциональные методы решения уравнений, о которых речь пойдет ниже.

Рассмотрим уравнение

F(x, д(х)) = F(x, /г(х)),     (1)

где F^x, у) —- функция двух переменных, д(х\ й(х) — функции одной переменной. Ясно, что оно является следствием уравнения

д(х) = h(x)           (2)

области допустимого значения (ОДЗ) уравнения (1). Кроме того, если х₀ содержится в ОДЗ уравнения (1) и функция F(x₀, у) является постоянной, то х₀ — решение уравнения (1).

Пусть х₀ — решение уравнения (1). Положим f = F(x, у). Тогда х₀ является решением уравнения

f(gUY) = f(h(.xY),        k3)

для которого, как показано в [1] и [2], можно использовать свойства функции fkyY Справедливо утверждение, доказательство которого аналогично доказательству утверждения 1 в [1].

Утверждение 1. Если п , F^,y)= YfMy где f^x) — некоторые функции (т. е. F(x, у) является многочленом относительно переменной yY то функция F(x, gtxY) -- F(,x, /г(х)) может быть представлена в виде произведения двух функций, одна из которых равна д(х) - h(xY

Пример 1. Решите уравнение

(г² -1)²+ х^² -1) = 4 + 2х.

Решение. Уравнение имеет вид (1), при этом

F(x, у) = у² + ху, д(х) = х² -1, h(x) = 2.

Разделив многочлен F(x, g(xY) --F(x, h(x)) = х⁴ + х³ - 2х² - Зх - 3 на двучлен д(х) - h(x) = х² - 3, получим х² + + х + 1. Таким образом, уравнение равносильно совокупности двух уравнений: х² - 3 = 0 и х² + х + 1 = 0. Отсюда следует, что решениями уравнения будут ± 4з.

Чтобы сформулировать следующее утверждение, введем необходимые понятия.

Пусть задана функция F(x, у^-) с областью определения D(FY Число х будем называть допустимым для F(x, у), если найдется число у такое, что пара (х, у) е D(FY Так, например, у функции lg(|i/|x) числа х > 0 являются допустимыми, а числа х < 0 не являются.

Функцию F(x, у) назовем строго возрастающей (убывающей) по перемен ной у на множестве У, если из того, что (х; у^, (х; у₂) ^е D(F\ у\ < у^ и У\, у^ G У, следует, что F(x; у^ ) < F(x; у₂) (соответственно F(x; у^) > F(x; y-^Y Из определения вытекает, что функция F(x, у) является строго возрастающей по у на множестве У тогда и только тогда, когда для любого фиксированного допустимого X функция ((д') = F(x, у) будет строго возрастающей на У пВф (D(f) — область определения функции f(yYY

Например, функции х²у + у³, lg(x² + у) строго возрастают по у па R, а функция 1/|#| - 4ху — строго убывает по у на (0, -»).

Строго убывающие и строго возрастающие функции по переменной у на множестве У будем называть строго монотонными по у на У Если множество Y не указано, то считается, что У = R.

Пусть функция F(x, у) является строго монотонной по переменной у и х₀ — решение уравнения (1). Тогда функция Ду) - F(x₀, у) будет строго монотонной. Поскольку х₀ — решение уравнения (3), то согласно доказанному в [11 и [2] х₀ является решением уравнения (2). Отсюда получаем следующее утверждение.

Утверждение 2. Если функция F(x, у) является строго монотонной по перемен- ной у, то уравнения (1) и (2) равносильны па ОДЗ уравнения (1).

Пример 2. Решите уравнение

■^х2 + 3х +1 - -^2х2 -х + 3 = х 2 - 4х + 2.

Решение. Если переписать уравнение как

-^х2 + 3x4-1 -х2 + Зх + 1 =

= ^Зх2-х + 3 -х + 3, то легко заметить, что оно относится к виду (1), причем

F(x, у)- ^2х² + у + у,

д(х) = -х² + Зх + 1, h(,x) - -х + 3.

Функция F(.x, у) является возрастающей по переменной у, и, значит, уравнение равносильно уравнению х2 - 4х + 2 = 0.

Поэтому решениями исходного уравнения будут 2 ± V2.

Пусть функция F^x, у) определена на D(F). Она называется взаимно однозначной по переменной у на множестве У, если для любого допустимого х функция /(у) = F(x, у) является взаимно однозначной на У n D(f), т. е. если (х; у_г), (х; у^ е D(F), у_х * у₂ и y_v у₂ е У, то F(x; у_х) * F(x; у₂). Ясно, что строго монотонная функция по переменной у на множестве У будет взаимно однозначной лоу на У Если множество У не указано, то считается, что У - R.

Справедливо следующее утверждение, доказательство которого аналогично доказательству утверждения 2.

Утверждение 3. Если функция F(x, у) является взаимно однозначной по переменной у, то уравнения (1) и (2) равносильны па ОДЗ уравнения (1).

Пример 3. Решите уравнение

(х2 +■ l)V8x +16 - (х + 4)Vx4 4-х2 +1.

Решение. ОДЗ уравнения х >-2. Поскольку х — -2 не является решением уравнения, то оно равносильно уравнению

(х2 + 1)/^х4 +х2 +1 - (х + 4)Д/8х4О6 .(4)

Если примем

FU. у) = у/^у² -х² , у(х) = х² +1,

А(х) = х + 4, то уравнение (4) запишется как (1). Исследуем поведение функции F(x, у) по переменной у. Ясно, что она является нечетной по у. Так как

^(х.у)^ ^у2-х2 - у21 ^у2^-^^ =

= -X2/^у1 -х2)3 , то F'(x,y)<0 при всех у и х * 0. Очевидно, что х = 0 является решением уравнения (4). Далее будем считать, что х *0. В этом случае функция F(x, у) взаимно однозначна по у и, значит, уравнение (4) на ОДЗ эквивалентно уравнению х +1 = х + 4.

Последнее уравнение имеет два решения — (1 + ЛЗ)/2. Так как они входят в ОДЗ исходного уравнения, то получаем окончательный ответ: х = 0, х = (1 ± V13)/2.

Функция F(x, у) называется четной (нечетной) по переменной у, если из того, что (х; у) g D(F), следует, что (х; -у) е D(F) и F(x, у) = F(x, -у) (соответственно F(.x, -у) = -F(x. у)). Из определения следует, что функция F(x, у) четная (нечетная) по у тогда и только тогда, когда функция /"(у) = F(x, у) является четной (нечетной) для любого допустимого х.

Ясно, что если функция F(x, у) является четной по переменной у, то уравнение (1) является следствием совокупности уравнений

g(x) = h(x), g(x) = -h(x).      (5)

Пусть функция F(x, у) является четной и взаимно однозначной на [0, «] по переменной у и х0 — решение уравнения (1). Тогда функция /Ху) = F(x0, у) будет четной и взаимно однозначной на D(f) л [0, ~) и х0 — решение уравнения (3). Отсюда следует (см. [1], [2]), что х0 будет решением совокупности уравнений (5). Поэтому справедливо следующее утверждение.

Утверждение 4. Если функция F(x, у) является четной и взаимно однозначной на [0, «>) по переменной у, то уравнение (1) эквивалентно совокупности уравнений (5) па ОДЗ уравнения (1).

Пример 4. Решите уравнение х2^х2 + х -5)2+|(х2 + х -З^х = х4 +1.

Решение. ОДЗ уравнения х * 0. Оно имеет вид (1), причем

F(x, у^ = х²у² + |у/х|, д(х) = х² + х - 5,

h(x) = х.

Функция F(.x, у) является четной и строго возрастающей на [0, ™) по переменной у. Поэтому уравнение равносильно совокупности двух уравнений — х2 + х -5 = х, х2+х-5 = -х.

Отсюда следует, что решениями заданного уравнения будут ± V5, -1 ± Тб.

Ясно, что если функция F^x, у) — нечетная по переменной у, то уравнение

F(x, д(х» + F(x, Й(х» = О (6) эквивалентно уравнению

F(x, д(х)) = F(x, - h(x)).

Пример 5. Решите уравнение

^2х² -х +1 -   +1 + 4х² + х - 3 -

- Vx2 -х+5 = 0.

Решение. Уравнение имеет вид (6), причем

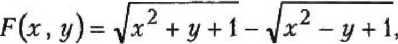
у(х)=х²-х, h(x) = х - 4.

Функция F^x, у) является нечетной и строго возрастающей по у. Поэтому уравнение на ОДЗ равносильно уравнению х - х = -х + 4, решениями которого являются ±2. Нетрудно заметить, что 2 входит в ОДЗ заданного уравнения, а -2 — нет, поэтому оно имеет единственное решение.

Функцию F(x, у), определенную на D(F), будем называть периодической (антипериодической) по переменной у, если для любого допустимого фиксированного х найдется положительное число Т (вообще говоря, зависящее отх) такое, что если (х, у) е D(F), то (х; у ±Т) е D(F) и F(x, у + Т) = F(x, у) (F(x, у + Т) = = -F(x, у)), т. е. для любого допустимого фиксированного х функция Ду) = F(x, у) является периодической (антипериодической). Число Т называется периодом (антипериодом) F(x, у) поу^. Так, например, функции sin((x² + 1)у), {х³ у) будут периодическими по у. Пусть функция F(x, у) — периодическая по переменной у. Если для любого допустимого х существует основной период у функции Ду) = F(x, у), равный Т(х), то функцию F(x, у) будем называть периодической по у с основным периодом Т(х).

Функция sin((x² + 1)у] будет периодической по у с основным периодом Т(х) = = 2 л/(х² + 1); функция же (х³ у} не имеет основного периода (при х = 0 она обращается в константу и, значит, не имеет наименьшего положительного периода). Очевидно следующее утверждение.

Если функция F(x, у) является периодической по переменной у с основным периодом, равным Т(х), то уравнение (1) является следствием совокупности уравнений

у(х) = Л(х) + пГ(х), (7) где не Z, на ОДЗ уравнения (1).

Предположим, что функция F(x, у) — периодическая по переменной у с основным периодом Г(х) и для любого допустимого х найдется число й(х) такое, что либо на <а(х\ а(х) + Т(х)], либо на [а(х); d(x) + Г(х)) функция F(x, у) взаимно однозначна по у. Пусть х₀ — решение уравнения (1). Тогда функция Ду) = F(x₀, у) является периодической с основным периодом Т(х₀), взаимно однозначной либо на (д(х₀); а(х₀) + Т(х₀)], либо на [я(х₀); а(х₀) + Г(х₀)) и х₀ — решение уравнения (3). Поэтому по утверждению из [2] Xq является решением совокупности уравнений

д(х) = Л(х) + пТ(х0), где и е Z, и, следовательно, семейства уравнений (7). Тем самым доказано следующее утверждение.

Утверждение 5. Пусть функция F(x, у) является периодической по переменной у с основным периодом Г(х) и для любого допустимого х найдется число а(х) такое, что или на (а(хо); й(х₀) + Т(х₀)], или на [с(х); д(х) + F(x)) функция F(x, у") взаимно однозначна по у. Тогда уравнение (1) и семейство уравнений (7) равносильны на ОДЗ уравнения (1).

Аналогично доказывается следующее утверждение.

Утверждение 6. Пусть функция F(x, у) является четной и периодической по переменной у с основным периодом Г(х). Если функция F(x, у) взаимно однозначна по у либо на [0; Г(х)/2), либо на (0; Г(х)/2], то уравнение (1) эквивалентно семейству уравнений дкх^ = ±й(х) + пТкхХ где п е Z, на ОДЗ уравнения (1).

Пример 6. Решите уравнение sin2 5х + cos2 2х = |(cos5x) /cos2x|.

Решение. ОДЗ уравнения х * я/4 + + 6л/2, где к ё Z. Ясно, что числа л/10 + кл/S, где к е Z, не являются решениями уравнения. Поэтому оно равносильно уравнению

(sin² 2х + cos² 2хУ)со5 2х| =

= (sin2 5х + cos2 2xy|cos 5xj,     (8)

которое имеет вид (1), причем

F(x, у) = (sin² у + cos² 2хУ]созу|, у(х) = 2х, h^ = 5х.

Функция F(x, у) является четной и периодической по у с основным периодом Т(х) = л. Кроме того, она строго возрастает по у на [0; л/2). Поэтому уравнение (8) эквивалентно семейству уравнений

±5х = 2х + пл.

где п е Z. Решениями семейства будут х = пл/3 их — пл/Ч, где п е Z. Поскольку эти х входят в ОДЗ исходного уравнения, то именно они являются его решениями.

Методы решения уравнений вида F(x, у(х)) = F(x, 7г (х)) излагались нами на математическом факультете Мордовского университета как в рамках спецкурса «Научные основы школьного курса математики», так и на занятиях по математическому анализу. Последующий анализ позволил сделать вывод о том, что рассмотрение указанных уравнений и методов их решения помогает сформировать у студентов-математиков единую систему знаний, способную обеспечить будущему учителю навыки решения профессиональных задач.