Урожайность зерновых культур в регионах ЦФО в 2010-2021 гг.: временные модели и территориальные особенности

Введение. Прогнозирование будущих значений временного ряда на основе его исторических значений является основой для планирования, управления и оптимизации объемов производства сельскохозяйственной продукции. Эта задача решается путем создания модели прогнозирования, адекватно описывающей исследуемый процесс.

В сфере ^ПК для прогнозирования уро^айности и объемов производства сельскохозяйственной продукции чаще всего используют регрессионные модели. Так, в работе О.В. Сидоренко и Т.И. Гуляевой [1] исследованы временные ряды уро^айности зерновых культур за 1960-2009 гг., при этом выявлены определенные закономерности колебаний природных условий сельскохозяйственного производства в целях заблаговременной локализации негативных последствий неуро^ая. По использованной в данной публикации эмпирической базе в нашей работе [2] выявлены следующие закономерности, носящие общий характер и имеющие определенное методологическое и методическое значение: при прогнозировании по регрессионным моделям следует анализировать не только результаты точечного прогноза, но и интервального, при этом аналитические расчеты необходимо дополнять анализом графиков модельных кривых с линиями доверительных границ; прогноз в коротких временных рядах по адаптивным моделям допустим лишь на шаг вперед, а по трендовым моделям – на один-два шага вперед, прогнозирование на больший горизонт допустимо только в целях выявления тенденции; применение квадратичных и кубических моделей недопустимо вследствие высокой вероятности изменения характера динамики временного ряда при экстраполяции моделей за пределами исторических данных; для повышения наде^ности прогнозирования следует строить объединенные прогнозы путем усреднения частных прогнозов по конкурирующим моделям; дальнейшее повышение качества прогнозов требует обращения к экспертной информации.

Наличие достаточно длинных временных рядов, однако, не всегда решает проблему низкой точности прогноза ввиду часто наблюдаемой цикличности. В этих случаях продуктивным, в частности, является предло^ение отказаться от обработки длинных временных рядов в пользу более коротких (например, 10летних), если за период наблюдения произошел «разворот» динамического ряда, т.е. первоначальная тенденция, выявленная на начальных стадиях наблюдения, была преодолена [3, с. 105].

Существуют и другие предло^ения, направленные на повышение точности прогноза. Так, автор работы [4], анализируя эмпирическую базу урожайности зерновых культур в условиях сухостепных зон Ни^него Повол^ья, взамен традиционного регрессионного анализа предлагает адаптацию и совершенствование математических моделей на основе искусственных нейросетевых структур различной архитектуры, используемых в четкой либо нечеткой постановке. Автор утверждает, что качество полученных нейросетевых моделей временных рядов уро^айности зерновых по характеристикам остатков свидетельствует о возмо^ности их использования, поскольку на уровне значимости α=0,05 они являются гомоскедастичными, некоррелированными и нормально распределенными. Однако для реализации этой задачи требуется разработку программного комплекса для автоматизации процедуры формирования (генерации), обучения и применения искусственных нейронных сетей (ИНС), обеспечивающих прогнозирование ме^годовой изменчивости уро^айности и учитывающих особенности сельскохозяйственных культур в засушливых условиях, что, в свою очередь, требует обоснования алгоритма предобработки данных, передаваемых в ИНС [5].

Цeль исслe^oʙаʜий . Изло^енные выше методы повышения наде^ности прогнозирования относятся к достаточно длинным рядам. Так, в работе [6] рассматриваются временные ряды по годовым данным с 1950 по 2015 гг., в других публикациях по объединению прогнозов так^е фигурируют длинные ряды. Им соответствуют валидные методы прогнозирования, такие как модель Бокса-Дженкинса, метод гармонических весов, метод адаптивного экспоненциального сглаживания с использованием трэкинг-сигнала, другие «тонкие» методы, применение которых в случае коротких временных рядов невозмо^но или затруднено. Но чаще всего исследователи имеют дело с временными рядами средней длины, охватывающими 10-15 лет. Во многих случаях их аппроксимацию мо^но проводить с помощью достаточно простых средств, например, с помощью процедуры «оценка кривой» пакета программ анализа данных общественных наук SPSS . В этой связи актуальными являются статистические исследования, направленные на выявление пределов применимости столь простых методов прогнозирования в рядах средней длины, адаптированной к высокой изменчивости показателей, органически присущей процессам АПК.

Услoʙи^, матeриалы и мeтo^ы. Решение поставленной задачи требует адекватного ИТ-инструментария. Для построения регрессионных моделей и визуализации результатов моделирования использован пакет статистических программ анализа данных общественных наук IBM SPSS Statistics Base 22. В качестве эмпирической базы использовали статистические данные по урожайности зерновых культур в регионах Центральной России за 2010-2021 гг.

Из широкого разнообразия графических и аналитических процедур пакета анализа данных SPSS Base использовались диаграммы последовательностей ( Sequence Plot ), процедура регрессионного анализа «приближение кривых» ( Curve Estimation ).

Peзультаты и oбсу^^eʜиe. Из графика исследуемого временного ряда урожайности зерновых культур в ЦФО за период 2010-2021 гг., представленного на рис. 1, видно, что динамика показателя характеризуется сильной изменчивостью с несколькими циклами подъема и спада, но в целом наблюдается рост показателя с его последующей стабилизацией. Отсюда следует, что при общей тенденции к росту уро^айности зерновых на протя^ении рассматриваемого двенадцатилетнего периода, динамика показателя мо^ет быть с достаточной точностью аппроксимирована гиперболической моделью, типичной в случае, когда неограниченное увеличение объясняющей переменной асимптотически прибли^ает зависимую переменную к некоторому пределу.

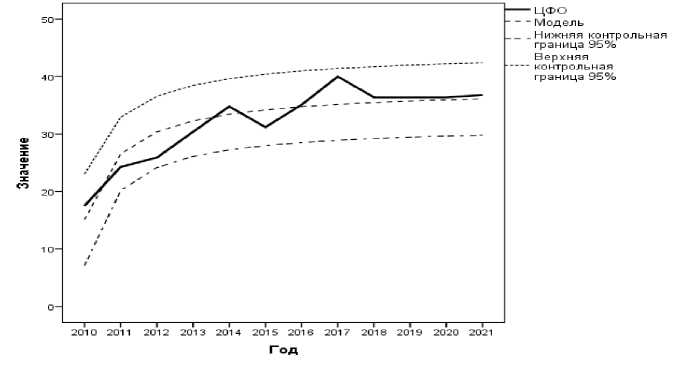
Рисунок 1 – Динамика уро^айности зерновых культур в ЦФО в 2010-2021 гг. Источники: [7, с. 783], [8, с. 669], [9, с. 677]

Судя по графикам ни^ней и верхней контрольных 95%-х границ, показанных на рисунке 1, гиперболический тренд уро^айности зерновых культур по ЦФО в целом достаточно хорошо аппроксимирует динамику показателя за 12-ти летний период, что подтвер^дается и числовыми характеристиками: коэффициент детерминации 0,850; критерий Фишера 56,563 значим на двустороннем р -уровне не ху^е 0,0005.

^налогично, гиперболический тренд характерен для большинства сельскохозяйственных регионов Центральной России (таблица 1): для девяти регионов (Белгородской, Вороне^ской, Курской, Липецкой, Орловской, Рязанской, Смоленской, Тамбовской и Тульской областей) критерий Фишера значим на р -уровне не хуже 0,001, а для Московской области и РФ в целом - на уровне не ху^е 0,01.

Таблица 1 – Параметры и показатели качества аппроксимации динамики уро^айности зерновых культур гиперболическими моделями

Регион	Код региона	β 0 предел, ц/га	|β 1 | рост, ц/га	Коэф. детерм.	Критерий Фишера	Знач.
РФ	1000	26,328	9,292	0,585	12,964	0,005**
ЦФО	100	38,034	22,945	0,850	56,563	0,000***
Белгородская обл.	1	48,653	31,236	0,911	102,316	0,000***
Брянская обл.	2	43,583	35,812	0,597	14,809	0,003
Владимирская обл.	3	23,242	6,929	0,440	7,857	0,019
Вороне^ская обл.	4	35,475	22,235	0,827	47,662	0,000***
Ивановская обл.	5	19,765	2,184	0,085	0,931	0,357
Калу^ская обл.	6	23,727	5,936	0,272	3,744	0,082
Костромская обл.	7	13,993	1,421	0,083	0,903	0,364
Курская обл.	8	47,460	31,812	0,792	38,169	0,000***
Липецкая обл.	9	39,658	22,783	0,770	33,482	0,000***
Московская обл.	10	28,729	7,748	0,577	13,655	0,004**
Орловская обл.	11	38,495	20,604	0,678	21,092	0,001***
Рязанская обл.	12	31,984	18,790	0,740	28,418	0,000***
Смоленская обл.	13	23,175	11,054	0,719	25,644	0,000***
Тамбовская обл.	14	36,595	24,988	0,818	45,002	0,000***
Тверская обл.	15	14,411	2,813	0,183	2,243	0,165
Тульская обл.	16	33,471	18,609	0,778	34,998	0,000**
Ярославская обл.	17	18,342	4,385	0,206	2,594	0,138

Примечание: *** р < 0,001; ** р < 0,01

В соответствие с моделью гиперболического тренда у = во+ в1/ x+£.                                     (1)

где у - урожайность, х - независимая переменная (номер члена временного ряда), ее параметры интерпретируются следующим образом: в о - предельное значение урожайности, ц/га; |в 1 - предельный рост урожайности, ц/га; £ - ошибка измерения. Согласно этой модели, в ЦФО в целом уро^айность зерновых культур за 12 лет выросла на 22,9 ц/га и достигла уровня 38,0 ц/га.

Для таких регионов ЦФО, как Владимирская, Ивановская, Калу^ская, Костромская, Тверская и Ярославская области, гиперболическую модель динамики уро^айности нельзя считать адекватной эмпирическим данным, поскольку расчетное значение р -уровня критерия Фишера превышает величину 0,01, принятую нами за нормативную. Особое место занимает Брянская область, в которой, несмотря на высокое значение р -уровня (0,003), более адекватной является линейная модель ( р -уровень не хуже 0,0005). Рисунок 2 иллюстрирует эту ситуацию: ширина доверительного 95% интервала в случае линейной модели значительно меньше, чем в случае гиперболической модели.

а                                    б

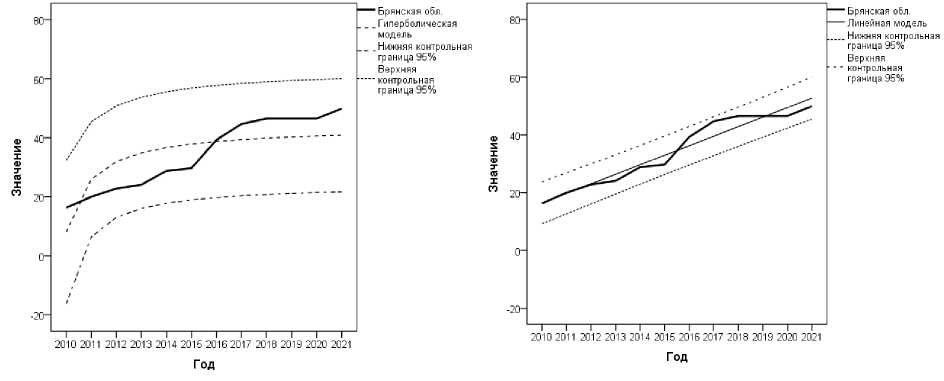
Рисунок 2 - Аппроксимация динамики урожайности зерновых культур в Брянской области в 2010-2021 гг.: а - гиперболической моделью; б -линейной моделью

На основании отмеченной закономерности можно предположить, что, по-видимому, в Брянской области имеются резервы для дальнейшего повышения урожайности зерновых культур.

В публикации [2] было рекомендовано в регрессионном анализе рассматривать результаты не только точечного, но и интервального прогноза, а так^е проводить анализ графиков модельных кривых с линиями доверительных границ. В случае Брянской области именно это обусловливает выбор ме^ду гиперболической и линейной моделью в пользу последней.

С учетом сказанного, типологический анализ проводим только для тех регионов, для которых гиперболические модели адекватны на р -уровне не хуже 0,001 (в таблице 1 эти регионы помечены тремя звездочками).

Гиперболические модели двухпараметрические (предельный уровень уро^айности и его максимальный рост), и валидным методом типологического анализа является кластерный иерархический анализ по методу Уорда, дополненный итеративным кластерным анализом по методу к -средних [10].

Вначале рассмотрим диаграмму рассеяния информативных параметров гиперболических моделей динамики уро^айности регионов – предельной уро^айности и роста уро^айности (рисунок 3). Как видно из рисунка, на диаграмме рассеяния проявляют себя три типологических синдрома: первый – центральный, включает в себя, помимо ЦФО в целом (метка 100), Вороне^скую, Липецкую, Орловскую, Рязанскую и Тульскую области (метки 4, 9, 11, 12 и 16 соответственно). Второй типологический синдром соответствует наибольшим значениям показателей и включает в себя два региона – Белгородскую и Курскую области (метки 1 и 8 соответственно). Третий типологический синдром отвечает наименьшим значениям показателей и включает в себя так^е два региона – Московскую и Смоленскую области (метки 10 и 13 соответственно).

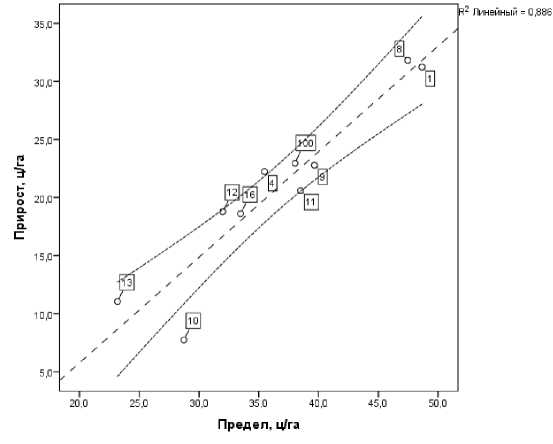
Рисунок 3 – Диаграмма рассеяния информативных параметров гиперболических моделей динамики уро^айности регионов ЦФО. Числа вблизи меток регионов отвечает их кодам согласно таблице 1: 1 – Белгородская обпасть, …, 16 – Тульская область, 100 – ЦФО

Визуальной типологии регионов полностью соответствуют результаты иерерхического кластерного анализа: на представленной на рисунке 4 дендрограмме на уровне сходства около 90% четко различаются именно эти три кластера: регионов-лидеров (кластер 2), регионов-аутсайдеров (кластер 3) и регионов центральной тенденции (кластер 1).

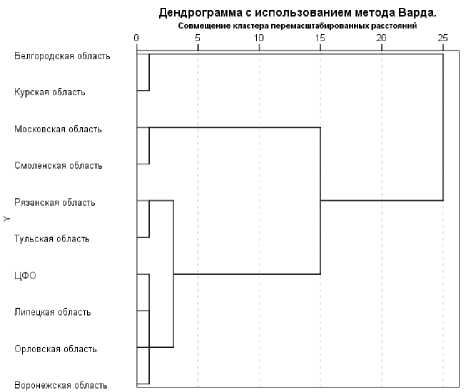
Рисунок 4 – Дендрограмма кластерного анализа регионов ЦФО

Результаты итеративного кластерного анализа по методу к -средних с тремя кластерами ( к =3) также полностью идентичны результатам иерархического кластерного анализа, что свидетельствует об устойчивости постулируемой типологии регионов. При этом кластеры хорошо разделены по обеим переменным, их распределения не пересекаются - рисунок 5.

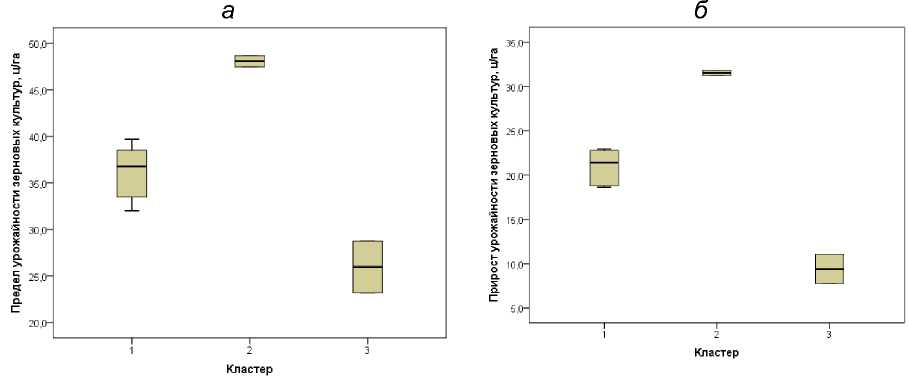
Рисунок 5 - Распределение параметров урожайности зерновых культур в ЦФО в 2010-2021 гг. по однородным кластерам регионов: а - предел урожайности; б - прирост урожайности

Заключение. Таким образом, поставленная цель статистических исследований достигнута. Показано, что с удовлетворительной для практики точностью тренд динамики уро^айности зерновых культур большинства регионов ЦФО мо^ет быть аппроксимирован гиперболическими моделями с ярко выра^енным стремлением уро^айности к максимально возмо^ному пределу по природно-климатическим условиям. В результате типологического анализа выявлены три характерных кластера регионов: лидеров (Белгородская и Курская области), аутсайдеров (Московская и Смоленская области) и регионов центральной тенденции (Вороне^ская, Липецкая, Орловская, Рязанская, Тульская области и ЦФО в целом). Ярким представителем кластера центральной тенденции является Вороне^ская область. Показано, что имеется статистически значимая корреляция между ростом урожайности и ее предельным значением.

Для таких регионов ЦФО, как Владимирская, Ивановская, Калу^ская, Костромская, Тверская и Ярославская области, гиперболическую модель динамики уро^айности нельзя считать адекватной эмпирическим данным. Особое место занимает Брянская область, в которой, несмотря на высокое значение р -уровня, более адекватной является линейная модель. Это позволяет предполо^ить, что в Брянской области имеются резервы для дальнейшего повышения урожайности зерновых культур.

Выявленные закономерности могут быть полезны при решении задач прогнозирования валового сбора зерновых культур в регионах ЦФО.

Благодарность. Авторы выражают глубокую признательность докто^у экономически^ наук, почетному ^аботнику высшего п^офессиона^ьного об^азовани^ Российской Феде^ации, п^офессо^у Вадиму Гео^гиевичу Шуметову за постановку задачи статистически^ исс^едований и участие в обсу^дении по^ученны^ ^езу^ьтатов.