Усиление бетонных балок углепластиком с учетом исходного состояния

В связи со значительным физическим износом существующего жилищного фонда все большее внимание уделяется методам и способам усиления существующих конструкций, в том числе имеющих значительные повреждения [1]-[3]. Необходимость в усилении существующих конструкций также возникает при реконструкции или техническом перевооружении существующих зданий и сооружений в связи с необходимостью увеличения действующих эксплуатационных или технологических нагрузок.

Для изгибаемых железобетонных конструкций, в том числе балок, одним из наиболее передовых и экономически эффективных способов повышения несущей способности является метод усиления путем устройства внешнего армирования в растянутой зоне из композитных полимерных материалов. При этом методе усиления чаще всего применяют углепластиковые Mirsayapov I..; Apkhadze G.; Nuguzhinov Zh.

Strengthening of concrete beams by CFRP considering initial state;

(Carbon) или арамидные (Kevlar) одно- или разнонаправленные холсты («мокрый» способ) и ламинаты («сухой» способ) на полимерном, чаще всего эпоксидном связующем [4]-[6]. При этом известно, что, в связи с особенностями композиционных полимерных материалов (достаточно низкий модуль упругости в сравнении со сталью), разрушение усиленных элементов в большинстве случаев происходит от раздробления бетона в сжатой зоне. Таким образом, в случаях, когда невозможно осуществить полную разгрузку существующих конструкций, необходимо учитывать начальное напряженно-деформированное состояние таких элементов.

Первым подходом по учету уровня разгрузки усиленных железобетонных элементов является упрощенная методика метода предельных усилий с введением условных коэффициентов к несущей способности или коэффициентов к расчетным сопротивлениям материалов. Применение данного подхода к решению поставленной задачи является в значительной степени приближенным учетом неполной разгрузки существующих конструкций, подлежащих усилению. В связи со значительной погрешностью в получаемых результатах с начала 2000-х годов он был полностью заменен иными более точными методами решения.

Второй подход, отраженный в действующей нормативной базе [7] в части расчета таких конструкций по нормальному сечению с учетом начального напряженного состояния, имеет ряд существенных недостатков, к которым можно отнести: использование в основе подхода метода предельных усилий с ограничением высоты сжатой зоны бетона граничной величиной, что приводит к значительному занижению фактической несущей способности, а также упрощенного учета начального напряженного-деформированного состояния с использованием условных коэффициентов.

К третьему подходу в решении задачи по возможному учету влияния начального напряженно-деформированного состояния на прочность нормальных сечений усиленных железобетонных элементов можно отнести использование методики нелинейной деформационной модели, описанной в работах [8]-[11]. Данная методика является в основе своей итерационным методом решения физически-нелинейных задач, однако, для целей учета начального состояния расчет производят в два последовательных шага с использованием параметров напряженно-деформированного состояния (деформаций, напряжений, кривизны и жесткости сечения), полученных на первом расчетном шаге, в качестве исходных начальных данных для итерационного расчета на втором расчетном шаге уже с учетом наличия элементов внешнего усиления.

Четвертым известным методом для получения достаточно точного решения поставленной задачи является применение метода конечных элементов с учетом «рождения» («монтажа») новых элементов внешнего усиления на определенном шаге физически нелинейного расчета [12], [13]. Данный подход, однако, в некоторых случаях усложняется значительной степенью трудоемкости вычислений и ограничениями в возможностях конкретных программных комплексов конечно-элементного анализа.

Нередко значения, получаемые по всем описанным методикам, дают значительно расходящиеся результаты. При этом наиболее точное решение, очевидно, получается при использовании подхода нелинейной деформационной модели и метода конечных элементов, которые, однако, в свою очередь требуют автоматизированного (шагово-итерационного) подхода к решению задачи.

Множественные экспериментальные исследования усиленных композитными материалами балок, представленные в работах [14]-[17], показали значительное увеличение несущей способности полностью разгруженных элементов и хорошую сходимость методики нелинейной деформационной модели нормального сечения в итерационной постановке решения задачи с опытными данными. Стоит отметить, что включение элементов усиления в работу происходит только при обеспечении требуемого уровня сцепления между бетоном и композитом, что хорошо продемонстрировано в работах [18]-[20].

Множественные теоретические исследования прочности и трещиностойкости усиленных композитными материалами элементов с учетом истории нагружения предпринимались E.Hamed [21], N. Plevris [22], O. Rabinovich [23], [24], Picard A. [25]. Проблематикой анализа длительной прочности и деформативности усиленных изгибаемых элементов занимались такие ученые, как K.N. Tan [26] и G. Al Chami [27].

Однако, упрощенной и при этом достаточно точной зависимости для определения прочности усиленных элементов с учетом их начального состояния в аналитическом форме исследователями получено не было.

Таким образом, целью авторов ставится получение аналитической и наиболее упрощенной методики для определения несущей способности нормальных сечений изгибаемых железобетонных элементов, усиленных композитными полимерными материалами в растянутой зоне, с учетом предыстории нагружения, основываясь на подходах нелинейной деформационной модели. Задачами исследования являются: получение точного значения коэффициента полноты эпюры в сжатой зоне бетона на основании кривых деформирования; получение аналитической зависимости для высоты сжатой зоны бетона в нормальном сечении в предельном состоянии после усиления с учетом начального напряженно-деформированного состояния элемента.

• 2    Materials and Methods

Основным преимуществом принятой в данной работе для дальнейшего исследования зависимости для определения коэффициента полноты эпюры в сжатой зоне бетона (т.е. соотношения высоты прямоугольной эпюры и более сложной), является хорошее совпадение с опытными кривыми деформирования, что может быть хорошо оценено сравнением площадей, ограничиваемых рассматриваемой трехлинейной диаграммой (рис. 1) и осью, по которой откладываются относительные деформации сжатия в бетоне (табл. 1).

Таблица 1. Сравнение значений коэффициента полноты эпюры в сжатой зоне бетона ω Table 1. Comparison of plot completeness coefficient values in the compressed concrete zone ω

Метод / Method	Коэффициент полноты эпюры сжатой зоны при классе бетона / Coefficient values in the compressed concrete zone
	В10	В15	В20	В25	В30	В35	В40	В50	В60
1	0.845	0.843	0.841	0.838	0.836	0.834	0.832	0.828	0.824
2	0.8	0.8	0.8	0.8	0.8	0.8	0.8	0.8	0.8
3	0.786	0.786	0.786	0.786	0.786	0.786	0.786	0.786	0.786
4	0.859	0.855	0.850	0.844	0.841	0.837	0.833	0.824	0.814
5	0.873	0.866	0.857	0.849	0.844	0.839	0.834	0.824	0.814
1    – экспериментальная зависимость [28]; 2    – значения, приведенные в действующем нормативе [29]; 3    – двухлинейная диаграмма деформирования бетона [29]; 4    – трехлинейная диаграмма деформирования бетона (рис. 1); 5    – криволинейная диаграмма деформирования бетона [30].

Для двухлинейной диаграммы деформирования коэффициент полноты эпюры не зависит от класса бетона (при классе бетона до В60 - ε_{b 1, red} = 1.5 мм/м) и принимается равным:

ω = 1 - 0.5 ε ^{b 1, red} = 0.786,                                      (1)

ε b 2

Для принятой трехлинейной диаграммы (рис. 1) коэффициент полноты эпюры определяется из следующего выражения:

ω = 1 - 0.2 ε ^{b 0} - 0.5 ε ^{b 1} ,                                       (2)

ε b 2       ε b 2

где: ε _{b 1} = 0.6 R_b / E_b , ε _{b 0} = 0.002, ε _{b 2} = 0.0035 - фиксированные для данного класса бетона параметрические точки диаграммы деформирования сжатого бетона.

После введения значений параметрических точек трехлинейной диаграммы в формулу (2) коэффициент полноты эпюры в сжатой зоне ω с достаточной точностью окончательно будет равен:

Mirsayapov I..; Apkhadze G.; Nuguzhinov Zh.

Strengthening of concrete beams by CFRP considering initial state;

a = 0.885 - 85 -b- . Eb

Как видно из табл. 1 и рис. 2 среднее расхождение коэффициента полноты эпюры, принятого далее в расчетной методике (рис. 4) относительно экспериментальных данных, принятых в [18], составляет менее 0.5 %. При этом расхождение между значениями, вычисленными по более сложной и совершенной криволинейной диаграмме деформирования и опытными значениями составляет 1.0 %.

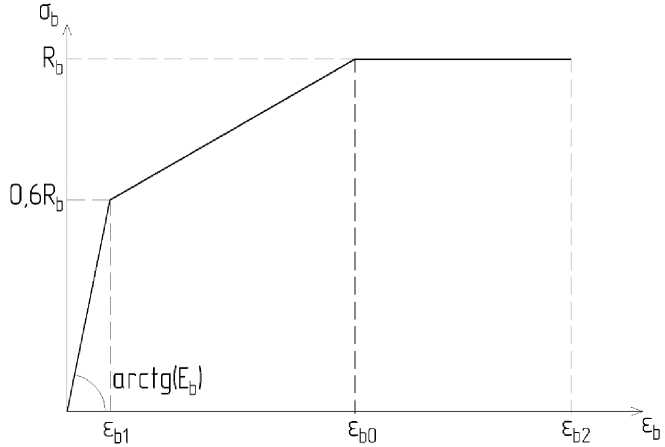
Рис. 1 - Трехлинейная диаграмма деформирования сжатого бетона

Fig. 1 - Three-line diagram of compressed concrete deformation

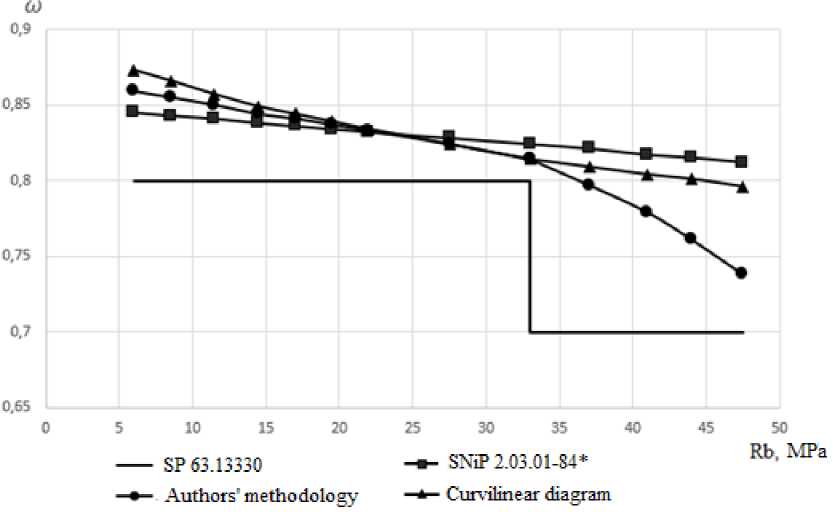
Рис. 2 - График изменения ω в зависимости от прочности бетона R _b

Fig. 2 - Graph of changes in ω depending on concrete compressive strength R _b

Граница переармированности изгибаемых конструкций, усиленных внешним армированием, как и для железобетонных элементов, определяется граничной высотой сжатой зоны ξ _Rf , вычисляемой по следующему выражению, получаемому из соответствующих соотношений при сохранении плоского поворота нормальных сечений:

£ _ xRf _      CD

_{1 +} * fu + J ’                                      (4)

1 + —----

^S b 2

где s b - начальные деформации на сжатой грани бетона до усиления (рис. 3), определяемые по следующей формуле:

s b _

M ⁰

EL

• x b ,

здесь:

M ⁰ – фактический максимальный изгибающий момент, воспринимаемый нормальным сечением после возможной разгрузки до устройства внешнего усиления;

xm0 – усредненная высота сжатой зоны в сечении элемента на участке с трещинами или без трещин после возможной разгрузки до устройства внешнего усиления;

(EI)  - фактическая жесткость железобетонного сечения после возможной разгрузки до устройства внешнего усиления, определяемая в зависимости от наличия или отсутствия трещин по упрощенной методике при треугольной эпюре в сжатой зоне бетона или на основании нелинейной деформационной модели.

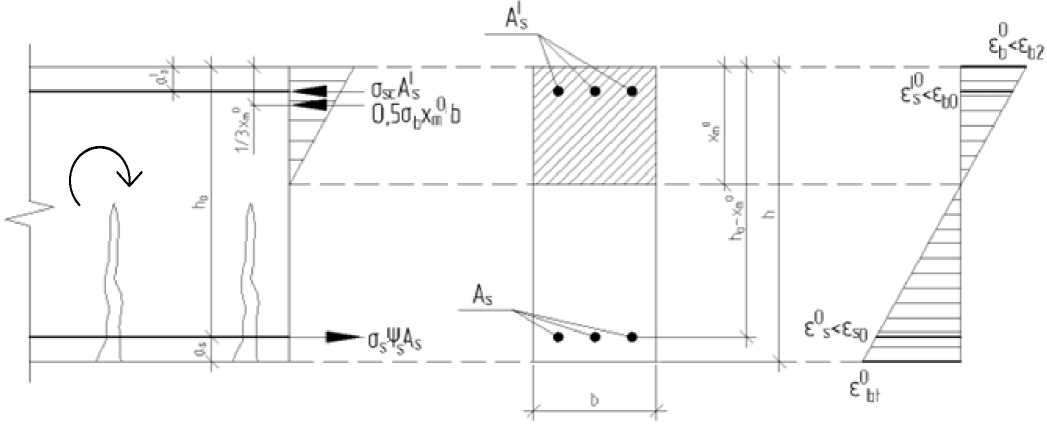
Рис. 3 - Расчетная схема нормального сечения изгибаемого элемента до усиления

Fig. 3 - Design diagram in the normal section before strengthening

В случае разрушения усиленного внешним армированием железобетонного элемента по нормальному сечению по растянутой зоне сечения (первый случай нормального сечения) влияние начального состояния элемента на его несущую способность после усиления невелико и может не учитываться, однако, данный случай, как уже было сказано выше, в реальной практике проектирования и реконструкции встречается нечасто в связи с низким модулем упругости композитных материалов, используемых для внешнего усиления в растянутой зоне.

Таким образом, для случаев при £ <  £ _Rf выражение для определения предельного изгибающего момента, воспринимаемого нормальным сечением усиленного железобетонного элемента прямоугольного сечения, не учитывает начальное деформированное состояние элемента и в наиболее простом и достаточно точном виде метода предельных усилий выглядит следующим образом:

M ult = R b ■ b ■ x ■ ( h о - 0.5 x ) + R sc ■ A'. ( h 0 — a . ) + R' A f 'a , ,                      (6)

где x – высота сжатой зоны в предельном состоянии, определяемая по формуле:

R . • A . - R_sc • A ’ + R_f • A_f R_b • b

Для случаев при § >  £ _Rf очевидно, что напряженное состояние (деформации) в бетоне в сжатой зоне элемента до усиления при неполной разгрузке будет оказывать существенное влияние на прочность нормального сечения после усиления.

Приведем расчетную схему для определения напряженно-деформированного состояния нормального сечения элемента с неполной разгрузкой в момент усиления внешним армированием в растянутой зоне однонаправленными холстами (ламелями) на полимерном вяжущем до (рис. 3) и после усиления (рис. 4) соответственно. Параметры напряженно-деформированного состояния до усиления приняты с верхним индексом «0», после усиления – без верхнего индексного обозначения.

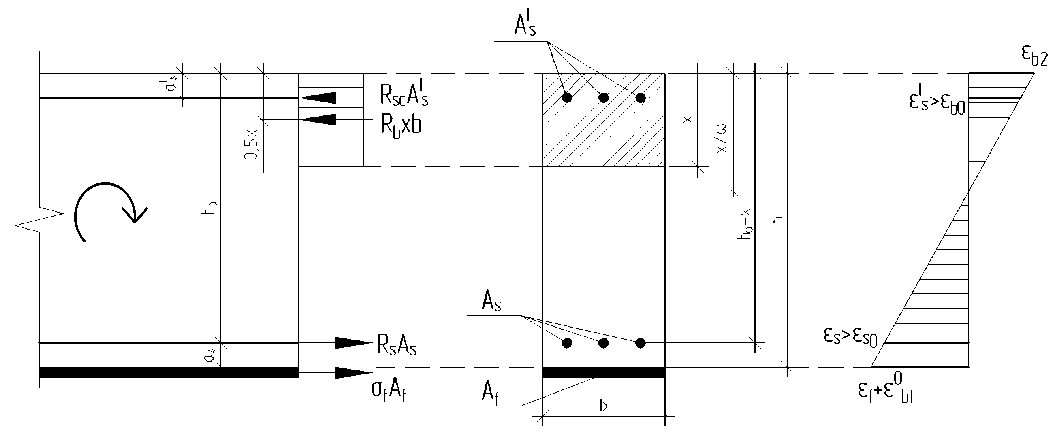
Рис. 4 - Расчетная схема нормального сечения усиленного изгибаемого элемента

Fig. 4. Design diagram in the normal section of a strengthening bending element

Запишем в общем случае равенство внутренних продольных усилий в нормальном сечении элемента после усиления при принятой расчетной схеме (рис. 4):

R b • b • x + R_S c • A . = R , • A , + о f • A f ,

Неизвестную величину о_f в уравнении (8) выразим через предельные деформации в бетоне сжатой зоны из гипотезы плоских сечений в соответствии с рис. 4:

^о f

= ^£ f • E f =

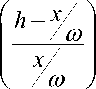
^£ b 2 • ^E f ,

С учетом того, что железобетонный изгибаемый элемент в момент перед усилением имел начальные относительные деформации на уровне растянутой грани бетона равные ebt, то напряжения в материале внешнего усиления уменьшаются до величины, определяемой по следующему выражению:

° f

= ( ^£ f

^£ 0 У ^Ef =

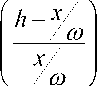
■ ^£ b 2 ■ ^E f

—

^£ bt E f

,

При этом величина начальных деформаций в бетоне на растянутой грани £ 0 определяется в зависимости от наличия или отсутствия трещин в растянутой зоне бетона до усиления (рис. 3):

" b = ( EMI )J ^{h —} x m ) ,

Подставляя выражение (10) с учетом величин, определяемых по (3), (11), в уравнение (8), получаем окончательную форму квадратичного уравнения относительно высоты сжатой зоны бетона при принятой прямоугольной эпюре в предельном состоянии усиленного элемента, имеющую следующий вид:

^R b ■ b ■ x ^{2 —} ( ^R s ■ A S ^{— R} sc ■ A S ^{— E}f ■ ^A f ’( ^£ b 2 + ^£ bt ) ) ■ x ^{— E}f ■ ^A f • ^£ b 2 ■ h ■ ® = ⁰ ,            (12)

Окончательная форма выражения для определения высоты сжатой зоны бетона в предельном состоянии усиленного внешним композитным армированием изгибаемого элемента с учетом начального состояния нормального сечения до усиления будет иметь следующий вид:

R . A S — R c A — E f A f ( b 2 + " b ) + J( R . A . — R sc A — E f A f £ 2 + £ 0 ) ) 2 + 4 ■ R f b 2 hb a x =-----------------------------------------------------------------------

• 2    ■ R b b

Для вычисления предельного изгибающего момента в рассматриваемом сечении (рис. 4) в предельном состоянии при ^ >  ^ _Rf с учетом высоты сжатой зоны, определенной по выражению (13), наиболее рациональным является его определение относительно оси, проходящей по растянутой грани элемента. В этом случае окончательное выражение для определения предельного изгибающего момента будет иметь вид:

M_uit = R b ' b ■ x ■ ( h — 0.5 x ) + R_sc ■ A ’ ■ ( h — a ’ ) — R s • A s ■ a s .                      (14)

• 3    Results and Discussion

Произведем сравнение результатов, получаемых по результатам итерационных расчетов в рамках нелинейной деформационной модели в два расчетных шага (до усиления и после усиления) с результатами, получаемыми по предлагаемой аналитической авторской методике.

В качестве сравнения примем условное прямоугольное железобетонное сечение 200x500 мм с арматурой в растянутой (3Ø20 мм А500) и сжатой зоне (3Ø12 мм А500). Бетон балки принят класса В25. Усиление производится в растянутой зоне углеродным холстом на эпоксидном связующем с расчетным сопротивлением композита R _f = 1100 МПа, модулем упругости композита E _f = 75 000 МПа и расчетной площадью сечения A _f = 400 мм² (нанесение композита в два слоя). За начальную стадию до усиления принимаем 80 % от предельного изгибающего

момента, воспринимаемого нормальным сечением железобетонного элемента до усиления, то есть разгрузка конструкции при усилении практически не производится.

Результаты расчетов согласно нелинейной деформационной модели представлены на рис. 5 и рис. 6 в виде мозаик, полученных автоматизированным способом с применением свободного программного обеспечения на сетке элементарных площадок размерами 10х10 мм.

Как видно из рис. 5 (а) при 80 % от первоначального предельного изгибающего момента ( M U0lt = 175.0 кН*м) относительные деформации на наиболее сжатой грани бетона составили s b = 0.98 мм/м, на наиболее растянутой грани элемента - s ^t = 1.87 мм/м (в сечении с трещиной). Согласно рис. 5 (б) растягивающие напряжения в нижней арматуре составляют a S = 362.8 МПа, сжимающие напряжения в верхней арматуре составляют а ^Ос = 182.9 МПа.

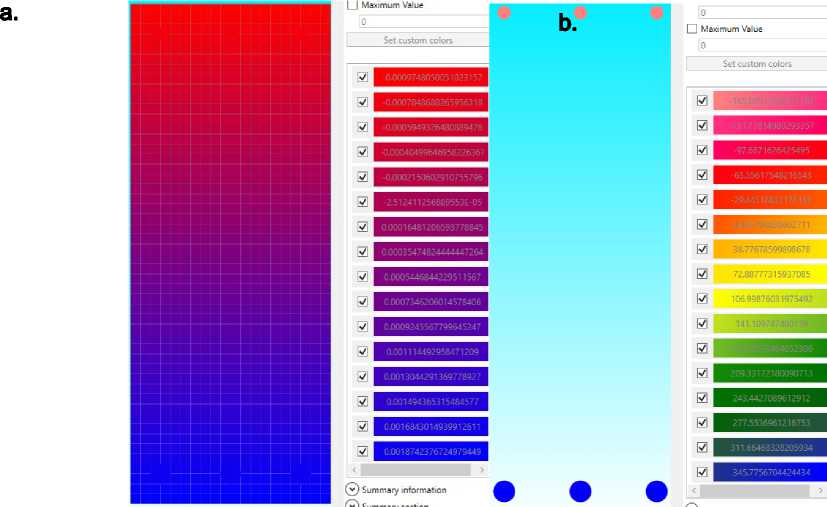
Рис. 5 - Начальное состояние элемента до усиления

(a – распределение деформаций в бетоне, b – распределение напряжений в арматуре)

Fig. 5 - Initial state of the element before strengthening

(a – distribution of deformations in concrete, b – distribution of stresses in reinforcement)

Рис. 6 - Состояние элемента в предельном состоянии после усиления

(a – распределение деформаций в бетоне, b – распределение напряжений в арматуре)

Fig. 6 - Initial state of the element in the limiting state after strengthening

(a – distribution of deformations in concrete, b – distribution of stresses in reinforcement)

В предельном состоянии несущая способность нормального сечения рассматриваемого усиленного внешним армированием изгибаемого элемента, согласно нелинейной деформационной модели, составила величину M _ultНДМ = 224.0 кН*м, что соответствует увеличению несущей способности элемента на 28 %. При этом разрушение в нормальном сечении произошло от раздробления бетона в сжатой зоне. Из рис. 6 в предельном состоянии усиленного элемента: относительные деформации на наиболее сжатой грани бетона составили Ьь = Ьъ ₂ = 3.45 мм/м; деформации в растянутой арматуре - s_s = 5.87 мм / м >s _{s 0} = R s / E_s , но при этом не достигают временного сопротивления разрыву арматурных стержней; напряжения в растянутой арматуре равны расчетному сопротивлению стали о ; = R s = 435 МПа. При этом растягивающие напряжения в композитном материале внешнего продольного усиления составили всего о f = 337.6 МПа (в сравнении с о_f = 442 МПа - при полной разгрузке конструкции), что значительно меньше его расчетного сопротивления ( R_f = 1100 МПа). Величина высоты сжатой зоны бетона в предельном состоянии составила 170 мм, что больше его граничной величины x .

Rf

Значение высоты сжатой зоны усиленного сечения в предельном состоянии, вычисленное по предложенному выражению (13) составило величину x / = 171.3 мм, что хорошо соответствует величине 170 мм, полученному согласно нелинейной деформационной модели.

Предельный изгибающий момент, воспринимаемый рассмотренным нормальным сечением в предельном состоянии по формуле (14) составил M_ult = 230.8 кН*м, что достаточно точно согласуется с полученным значением в рамках расчета по нелинейной деформационной модели ( М _и11 Н _Д М = 225.0 кН*м). Расхождение в полученных результатах определения несущей способности усиленного внешним армированием элемента с учетом начального напряженно-деформированного состояния по авторской методике относительно нелинейной деформационной модели составило менее 3.0 %.

• 4    Conclusions

Полученные выражения (13) и (14) применимы для определения предельного изгибающего момента усиленных изгибаемых элементов как прямоугольного, так и таврового сечения при высоте сжатой зоны, располагаемой полностью в полке элемента.

Предлагаемая методика для определения предельного изгибающего момента элементов, усиленных в растянутой зоне внешним армированием из композитных полимерных материалов на углеродном или арамидном волокне, позволяет:

• 1.     Учесть  начальное напряженно-деформированное состояние усиливаемых

• 2.     Определять долю снижения несущей способности частично разгруженных

• 3.     Получать хорошую сходимость по определению предельного изгибающего момента

изгибаемых элементов при их неполной разгрузке;

изгибаемых конструкций в сравнении с полностью разгруженными, что подтверждается имеющимися экспериментальными данными (снижение несущей способности до 15 %).

в сравнении с результатами, получаемыми по нелинейной деформационной модели или методом конечных элементов, с погрешностью не более 3 % при отсутствии необходимости проведения трудоемких итерационных вычислений.

• 5    Conflict of Interests

The authors declare that there is no conflict of interest. Authors made equivalent contributions to the publication.

Mirsayapov I..; Apkhadze G.; Nuguzhinov Zh.

Strengthening of concrete beams by CFRP considering initial state;