Using AHP Method for Educational and Vocational Guidance

Автор: Essaid EL HAJI, Abdellah Azmani, Mohamed El Harzli

Журнал: International Journal of Information Technology and Computer Science(IJITCS) @ijitcs

Статья в выпуске: 1 Vol. 9, 2017 года.

Бесплатный доступ

This work focuses on the use of multi-criteria decision-making method AHP for using in educational and vocational guidance. Analytical Hierarchy Process (AHP), proposed by the mathematician Thomas Saaty in 1980, is a method of analysis greatly used in the context of a multi-criteria analysis; it allows the comparison and the choice between the preset options. To achieve this goal, a vital work, preceded the use of the AHP method, which consists in doing a prototyping of trades according to the guidance criteria and sub-criteria. The IT system based on this method allows the student to find, firstly, the activities' sectors which are the most appropriate to his/her profile, to choose subsequently the trades and finally, to identify, the potential training paths.

Еще

Educational and Vocational Guidance, AHP, multi-criteria analysis, RIASEC, Big 5

Короткий адрес: https://sciup.org/15012606

IDR: 15012606

Текст научной статьи Using AHP Method for Educational and Vocational Guidance

Published Online January 2017 in MECS DOI: 10.5815/ijitcs.2017.01.02

The advent and rapid evolution of information and communications technologies (ICT) have paved the way toward the development of a multitude of tools for educational use. These tools have greatly contributed to not only improving the quality of education but also in covering the shortfall and therefore representing an alternative: e-learning and guidance assisted by the computer are two testimonies.

In fact, Guichard and Hutteau [1] do not see any advantage of the in-class guidance compared to that based on the use of the computer tool. In addition, others [2-4] advocate that the guidance based on IT presents various advantages: Free or less expensive in relation to a consultation with a specialist, more interactive, promoting the autonomy, Etc.

This awareness has given a great boost to the development of software to aid in educational and vocational guidance; however, it does not exist up to now a global and universal doctrine of guidance. This limits the role of the intervention of these IT tools.

In this paper, we use the AHP method in order to implement a system for educational and vocational guidance, which allows a student to build his/her professional project in four steps.

A. Step1: choice of activities' sectors

In this step, we propose a set of activities' sectors (education, teaching, Medicine, nature, etc.) the most suitable (appropriate) to the student profile, based on a set of criteria.

B. Step 2: choice of trades

In general, each sector includes a wide range of professions, for example in the field of medicine; there are the trades: doctor, pediatrician, pharmacist, midwife, etc.). Other criteria are taken into account in this step, such as educational data because each trade requires special training. In this step, the system proposes a set of trades that are the most appropriate to the student profile.

C. Step 3, choice of training

Depending on the trades selected in the previous step, the system offers the possible training for such a job.

D. Step 4, Choice of training path

Often the same training is accessible via several different paths. For a student, choosing a training path is dictated by several factors of pedagogical nature (notes, skills, abilities, etc.), socio-economic (social class, job of parents, etc.), cultural and even religious nature in some societies.

The process is referred to in the Figure 3.

II. T HE A NALYTICAL H IERARCHY P ROCESS

This paragraph is content to present an outline of the AHP method by focusing on the different stages of this process.

A. General presentation

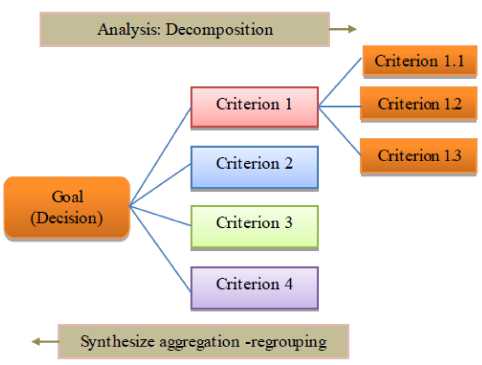
AHP (Analytical hierarchy process), proposed by Saaty [5] is one of the strongest and the most used methods in the context of multi-criteria analysis [6]. It is based on the decomposition of a complex problem of decision into criteria and on the synthesis and aggregation of weight associated with the different criteria for different levels of the hierarchy. The preferences between criteria are expressed by the weight wj from comparison matrix by pair between criteria with the same level of the hierarchy according to a scale of ration semantics [6].

And w = .

< w n V

B. Steps of an AHP analysis [7-9]:

An AHP analysis is decomposed into following steps:

• The hierarchical structuring of the problem: The first phase of each AHP analysis is to structure the decision problem into criteria and sub-criteria in the form of a graph (figure1).
• Construction of a matrix of judgment: It is often difficult for policymakers to associate with precision the weight corresponding to the different attributes. AHP helps to determine the values for each attribute using the judgments of decision makers or data based on a standard scale. These weights are stored in a matrix called pairwise comparison matrix (or matrix of judgment). The judgments are expressed in cardinal values and each a ij judgment indicates how much the attribute 'i' is more important than the attribute 'j'.

f a ll

A =

I a nl

a nn V

To construct the matrix of judgment, the decision maker defines the preferences that he has in respect with each pair of criteria and sub-criteria. These preferences verbally expressed, will be translated into digital forms according to the table 1.

Table 1. Table of equivalence of preferences

Verbal Scales	Digital Scales
The two criteria are equal	1
The criterion dominates moderately the other (a little more important)	3
The criterion strongly dominates the other (more important)	5
The criterion dominated very strongly the other (much more important)	7
The criterion is absolutely dominant (absolutely more important)	9
The intermediate values to refine the judgments	2, 4, 6, 8

The following table presents a decision matrix consisting of three criteria:

Table 2. Matrice of preferences equivalence

	Criterion1	Criterion2	Criterion 3
Criterion1	1	7	3
Criterion2	1/7	1	5
Criterion3	1/3	3	1
Total	31/21	11	9

This matrix shows that the criterion 1 (C1) dominated very strongly the Criterion 2 (C2).

C. Determining a priority vector containing the weights of criteria

The relative weight of each criterion is calculated by respecting the proportionality between the notes of comparison assigned to different criteria and the condition: sum of weight=1

The judgment matrix is a square matrix A having n attribute whose relative weights are w 1 , w 2 … w n . The weights of the attributes are measured with respect to each other according to the equation 2.

w aij = w Vi, j = 1,2,...,p (2)

D. Study of the consistency of the matrix of judgment

The consistency of checking the choice of the weights is to detect the inconsistency and, if necessary, to correct the affected weight. For this, we calculate a vector of

Table 3. Example of a matrix of standardized comparison

Criterion1 Criterion2 Criterion3 weight Criterion1 0.68 0.64 0.33 0.55 Criterion2 0.10 0.09 0.55 0.25 Criterion3 0.23 0.27 0.11 0.20 consistency CR, with:

Where CI is the indicator of consistency that is given by the equation 5, and RI: "Random Index" is a number function of n, indicated in tables ad hoc.

Table 4. Array of indices RI

n	3	4	5	6	7	8	9	10
RI	0,58	0,90	1,12	1,24	1,32	1,41	1,45	1,49

λ max - n n - 1

Where n is the number of elements to compare (rank of the matrix of preferences)

λ = (Cij.Wj max W i,j j

Where C ij are the elements of the matrix of judgment and W j the elements of the weight vector.

If CR> 0.1, we need to review the judgments expressed through the weights of the matrix of preferences.

E. Comparative study of alternatives to choose the best

In this step, we calculate the relative importance of the alternatives in relation to the indicators of each criterion and a matrix of preference is calculated, (we) obtain the vector of the relative importance of the alternatives in relation to each criterion.

Once the vectors of the relative importance of the alternatives in relation to the indicators are determined, we move on to the calculation of relative importance of the alternatives with regard, this time, to the criteria and, then, to calculate this importance in relation to the objective.

III. U SING AHP M ETHOD FOR E DUCATIONAL AND V OCATIONAL G UIDANCE

This section presents our approach of using the AHP method in the field of educational and vocational guidance. It presents an illustrative example by means of a sample case study.

A. The guidance is a problem of multi-criteria analysis

The educational and vocational guidance is a process that makes an appeal to several factors. In fact, the choice of guidance is often based on several criteria. Several studies have examined the demographic factors and personal which may influence the choice of professional and educational guidance. Among the personal factors, the level of general ability (10), culture or cultural status

(11), values and principles (12), self-esteem (13) selfefficacy (14), interests (14), personality [15] are decisive factors in the choice of the vocational and educational guidance of pupils. Among the demographic factors, the work of the parent (16), the level of study of the parents (17), ethnic origins (11), as well as the socioeconomic status, gender, and age of the student (10). These criteria do not have the same importance with respect to the different trades, i.e. the importance of a criterion varies according to each trade.

The use of the AHP method will allow us to structure the different criteria and to determine the importance of a criterion with respect to each other.

B. Use of the AHP method

• Prototyping of Trades: The prototyping trades step is a crucial and very important step in our work. It is to categorize the different trades depending on the set of criteria likely to intervene in the process of guidance. In fact, it is so rare and hard to find an expert capable, by himself, to make this categorization, because we are facing a situation where the data originated from several sources and fuzzy kind. To alleviate this problem we will use an original method which made calls to methods of treatment of the imperfect information and it is based on the notion of multi-expertise. This work will be developed in another article.

Prototyping of trades is done according to the principle proposed in the following figure:

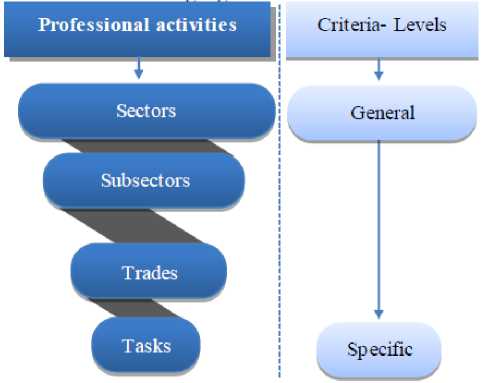
Fig.2. prototyping process of trades

• Proposed process: We propose a funnel guidance model which helps the student to gradually define his/her guidance project. The model used to generate, respectively, the sectors of activity, trades, training and training paths. For each level of the model, a set of criteria are taken into account and the student may have the option of stopping at any level or go to the end of the process. This flexibility allows the student to use the system in different stages of his/her school and academic career.

This model allows the student to find, firstly, the activities' sectors which are the most appropriate to his/her profile, to choose subsequently the trades and finally, to identify the potential training paths .

The choice of a training path is very important for both students and parents because choosing a suitable path can avoid many problems, such as unnecessary displacements (travels) and expenses.

This model is briefly presented in the following Figure

(Fig.3)

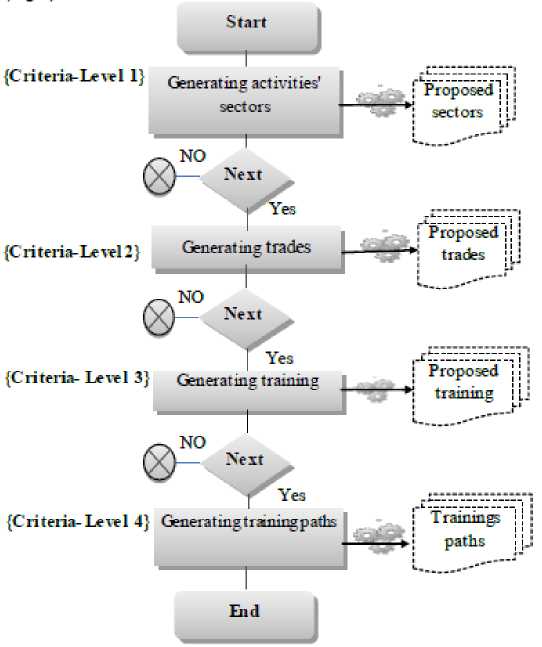
Fig.3. The proposed process to generate a guidance project

C. Case Study

Table 5. Criteria and sub criteria of the present study

Criteria	Indicators	Definition
	R	Realistic
	I	Investigator
Professional	A	Artist
Interests	S	Social
From Holland	E	Entrepreneur
	C	Conventional
	ET	Education and Teaching
	HM	Health and Medicine
Sub-interests	AG	Agriculture
	NE	Nature and Environment
	Op	Opening
	Co	Consciencieusite
Personality	Ex	Extraversion
Traits	Ag	Agreeability
	Ne	Neuroticisme

In this case study, we present an example while remaining in step I in our model. It, therefore, seeks , using AHP analysis, proposing to the concerned student the sector(s) of activities the most appropriate to his/her profile. To do this, we use the criteria: Professional Interests (PI) of Holland translated by the code RIASEC,

Personality Traits (PT) depending on the model Big 5 and the Sub-interests of the student. The criteria and indicators are reported in the following table:

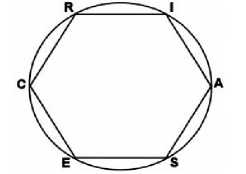
Fig.4. Circular representation of Holland RIASEC model

• Professional interests from Holland: Holland (1966) proposed a theory of "vocational choice", distinguishing six categories of professional interests (Realistic, Investigative, Artistic, Social, Enterprising, and Conventional), corresponding to different personality profiles. This classification is used to describe people, environments, and their interactions; it also serves to establish a typology of "Vocation choice" which explains "the vocational choice" of an individual. Holland has shown this typology with a

hexagonal pattern defining the psychological resemblances and interactions between personality types and environments [18], [19], [20].

• Personality Traits according to Big 5: Big 5 is currently considered as one of the most popular models for the analysis of personality [21 in 22] According to this model, five major areas of the personality: Nerveucisme, extraversion, openness, friendliness, and conscience are used to explain individual differences in the evaluations of Personality [22]. This evaluation model is today used as well for the question of recruitment than that of vocational training.
• Sub-interests: At a vocational choice, the wishes expressed by an individual must be respected as much as possible because it is so discouraged that someone has a job that he does not like. Therefore, the sub-interests are to be taken into consideration in the guidance process. In this case study, the subinterests are simply the areas of activities preferred by the individual and we have chosen the following sectors: Education and Teaching, Health & Medicine, Agriculture, Nature & Environment.

o Education and Teaching: Teacher, Professor, Educator, Guidance Counselor, etc.

o Health and Medicine: Doctor, Nurse,

Psychologist, Social Assistant, etc.

o Nature and Environment: Environmental

Advisor, Gardener, Engineer in protection of the environment, Geologist, Farmer, etc.

D. AHP process

a) Structuring of problem
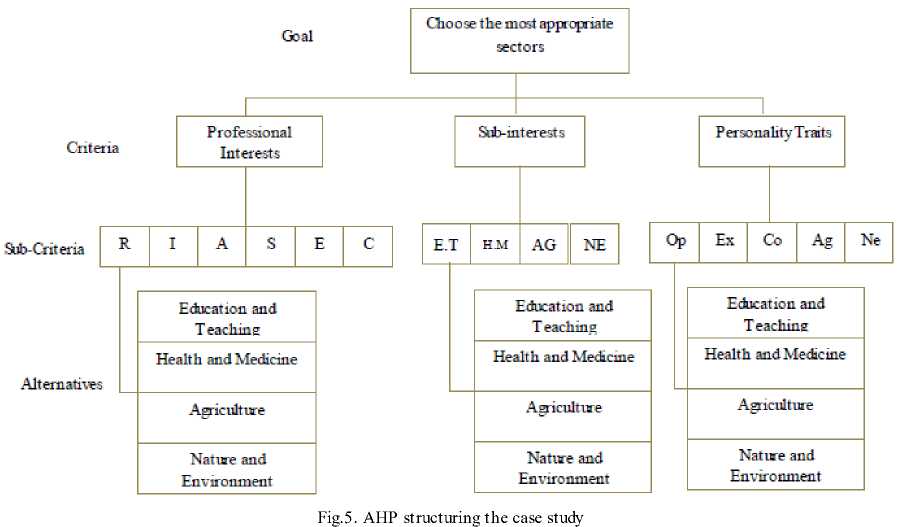
b) Processing and results

Matrix of the judgment of the first level (level criteria)

Relative Importance and standardized weight at the level of indicators (sub-criteria)

Table 6. The judgment matrix of the first level

	Professional Interests	Subinterests	Personality Traits	W
Professional Interests	0.65	0.69	0.56	0.63
Sub-interests	0.22	0.23	0.33	0.26
Personality Traits	0.13	0.08	0.11	0.11

Table 7. Relative importance of indicators RIASEC

IP	R	I	A	S	E	C	W
R	0.04	0.02	0.03	0.06	0.02	0.01	0.03
I	0.18	0.10	0.07	0.11	0.18	0.20	0.14
A	0.25	0.31	0.21	0.18	0.30	0.28	0.25
S	0.32	0.51	0.62	0.53	0.42	0.36	0.46
E	0.11	0.03	0.04	0.08	0.06	0.12	0.07
C	0.11	0.02	0.03	0.06	0.01	0.04	0.04

Table 8. Relative importance of indicators Sub-interests

Sub-interests	ET	HM	AG	NE	W
ET	0.60	0.66	0.54	0.44	0.56
HM	0.20	0.22	0.32	0.31	0.26
AG	0.12	0.07	0.11	0.19	0.12
NE	0.09	0.04	0.04	0.06	0.06

Table 9. Relative importance of indicators personality traits

TP	Ou	Ex	Ne	Ag	Co	W
Ou	0.22	0.32	0.31	0.19	0.31	0.27
Ex	0.07	0.11	0.22	0.11	0.18	0.14
Ne	0.03	0.02	0.04	0.06	0.02	0.04
Ag	0.65	0.53	0.40	0.56	0.43	0.51
Co	0.03	0.02	0.01	0.08	0.06	0.04

Weight local, global, and each indicator

Table 10. Weight global and each indicator

Criterion	Sub-criterion	weight
Pr. Int weight 0.63		local	global
	R I A S E C	0.03 0.14 0.25 0.46 0.07 0.04	0.0189 0.0882 0.1575 0.2898 0.0441 0.0252
Criterion	Sub-criterion	weight
Sub-interests weight 0.26		local	global
	ET HM AG NE	0.56 0.26 0.12 0.06	0.1456 0.0676 0.0312 0.0156
Criterion	Sub-criterion	weight
Traits. Per weight 0.11		local	global
	Op Ex Ag Ne Co	0.27 0.14 0.04 0.51 0.04	0.0264 0.0154 0.0044 0.0561 0.0044

Relative degree of success in the performance of indicators by each functional unit

Table 11. Relative degree of success of professional interests' indicators

Criterion Realistic (R)
R	ET	HM	AG	NE	W
ET	0.10	0.10	0.06	0.25	0.13
HM	0.10	0.10	0.06	0.25	0.13
AG	0.70	0.70	0.44	0.25	0.52
NE	0.10	0.10	0.44	0.25	0.22
Criterion Investigator (I)
I	EE	SM	AG	NE	W
ET	0.10	0.13	0.35	0.05	0.16
HM	0.50	0.65	0.35	0.77	0.57
AG	0.10	0.09	0.05	0.03	0.07

NE	0.30	0.13	0.25	0.15	0.21
Criterion Artist (A)
A	ET	HM	AG	NE	W
ET	0.44	0.44	0.44	0.44	0.44
HM	0.44	0.44	0.44	0.44	0.44
AG	0.06	0.06	0.06	0.06	0.06
NE	0.06	0.06	0.06	0.06	0.06
Criterion Social (S)
S	ET	HM	AG	NE	W
ET	0.42	0.42	0.36	0.41	0.40
HM	0.42	0.42	0.36	0.41	0.40
AG	0.08	0.08	0.07	0.05	0.07
NE	0.08	0.08	0.21	0.14	0.13
Criterion Entrepreneur (E)
E	ET	HM	AG	NE	W
ET	0.30	0.30	0.30	0.30	0.30
HM	0.10	0.10	0.10	0.10	0.10
AG	0.30	0.30	0.30	0.30	0.30
NE	0.30	0.30	0.30	0.30	0.30
Criterion Conventional (C )
C	ET	HM	AG	NE	W
ET	0.25	0.25	0.25	0.25	0.25
HM	0.25	0.25	0.25	0.25	0.25
AG	0.25	0.25	0.25	0.25	0.25
NE	0.25	0.25	0.25	0.25	0.25

Table 12. Relative degree of success of sub-interests' indicators

Criterion Education and Teaching (ET)
ET	EE	HM	AG	NE	W
ET	0.62	0.05	0.50	0.50	0.42
HM	0.21	0.05	0.36	0.36	0.24
AG	0.09	0.45	0.07	0.07	0.17
NE	0.09	0.45	0.07	0.07	0.17
Criterion Health and Medicine (HM)
HM	ET	HM	AG	NE	W
ET	ET	0.11	0.21	0.36	0.36
HM	HM	0.33	0.62	0.50	0.50
AG	AG	0.54	0.09	0.07	0.07
NE	NE	0.02	0.09	0.07	0.07
Criterion Agriculture (AG)
AG	ET	HM	AG	NE	W
ET	0.05	0.05	0.07	0.03	0.05
HM	0.05	0.05	0.09	0.03	0.05
AG	0.45	0.45	0.63	0.71	0.56
NE	0.45	0.45	0.21	0.24	0.34
Criterion Nature and Environment (NE)
NE	ET	HM	AG	NE	W
ET	ET	0.06	0.06	0.03	0.07
HM	HM	0.06	0.06	0.03	0.07
AG	AG	0.39	0.39	0.23	0.21
NE	9	9	3	1	0.59

Table 13. Relative degree of success of personality traits' indicators

Criterion openness (Op)

Op	ET	HM	AG	NE	W
ET	0.43	0.38	0.44	0.44	0.42
HM	0.14	0.13	0.11	0.11	0.12
AG	0.21	0.25	0.22	0.22	0.23
NE	0.21	0.25	0.22	0.22	0.23
Criterion Extraversion (Ex)
Ex	ET	HM	AG	NE	W
ET	0.42	0.42	0.42	0.42	0.42
HM	0.42	0.42	0.42	0.42	0.42
AG	0.08	0.08	0.08	0.08	0.08
NE	0.08	0.08	0.08	0.08	0.08
Criterion Nerveucisme (Ne)
Ne	ET	HM	AG	NE	W
ET	0.38	0.38	0.38	0.38	0.38

HM	0.38	0.38	0.38	0.38	0.38
AG	0.13	0.13	0.13	0.13	0.13
NE	0.13	0.13	0.13	0.13	0.13
Criterion Agreeability (Ag)
Ag	ET	HM	AG	NE	W
ET	0.42	0.42	0.42	0.42	0.42
HM	0.42	0.42	0.42	0.42	0.42
AG	0.08	0.08	0.08	0.08	0.08
NE	0.08	0.08	0.08	0.08	0.08
Criterion Consciencieusite (Co)
Co	ET	HM	AG	NE	W
ET	0.46	0.55	0.38	0.38	0.44
HM	0.23	0.27	0.38	0.38	0.31
AG	0.15	0.09	0.13	0.13	0.12
NE	0.15	0.09	0.13	0.13	0.12

Partial contribution of each functional unit to the overall performance objective

Table 14. Partial contribution of each functional unit to the overall performance objective

Prof .Interests

Ind R Ind I Ind A Ind S Ind E Ind C Indicator Result

Edu.Tch Hea.Med Agr Nat.Env

0.13 0.16 0.44 0.40 0.30 0.25 R 0.0189 Edu.Tch 0.22

0.13 0.57 0.44 0.40 0.10 0.25 I 0.0882 Hea. Med 0.25

0.52 0.07 0.06 0.07 0.30 0.25 X A 0.1575 = Agr 0.07

0.22 0.21 0.06 0.13 0.30 0.25 S 0.2898 Nat.Env 0.09

E 0.0441 C 0.0252 W= 0.63

Sub-interests

Ind. ET Ind. HM Ind. AG Ind. NE Indicator Result

Edu.Tch Hea.Med Agr Nat.Env

0.42 0.26 0.05 0.38 ET 0.1456 Edu.Tch 0.09

_0.24 0.49 0.05 0.38 HM 0.0676 Hea.Med 0.08

_{0 17} 0.19 0.56 0.13 X AG 0.0312 = Agr 0.06

^. 0.06 0.34 0.13 NE 0.0156 Nat.Env 0.04

W = 0.27

Personality Traits

IndOp IndAg Ind Ex IndCo Ind Ne Indicator Result

Edu.Tch Hea.Med Agr Nat.Env

0.42 0.42 0.42 0.44 0.38 Op 0.0264 Edu.Tch (ET) 0.04

0.12 0.42 0.42 0.31 0.38 Ag 0.0044 Hea.Med(HM) 0.03

0.23 0.08 0.08 0.12 0.13 X Ex 0.0154 = Agr(AG) 0.02

0.23 0.08 0.08 0.12 0.13 Co 0.0044 Nat.Env (NE) 0.02

Ne 0.0561

W= 0.11

Final results for assessment of the best performing functional unit.

Table 15. Final results for assessment of the best performing functional unit.

	Prof. Int	Traits.pers	Sub-interests	Total
Education and Teaching	0.22	0.09	0.04	0.35
Health and Medicine	0.25	0.08	0.03	0.36
Agriculture	0.07	0.06	0.02	0.15
Nature et environnement	0.09	0.04	0.02	0.15
Total	0.63	0.27	0.11	1.00

IV. C ONCLUSION AND P ROSPECTS

In this paper, the multi-criteria decision-making method AHP is used for educational and vocational guidance. Although the results obtained show how interesting is this method, it appears unable to deal with the fuzzy nature of the used data. In fact, and as a logical continuation of this work, we aim to complete it using the FAHP method that will allow us to process the fuzzy nature of manipulated data.

Список литературы Using AHP Method for Educational and Vocational Guidance

J. Guichard and M. Hutteau, “Psychologie de l'orientation,” 2006
F. Rivas, “Tecnología informática en asesoramiento vocacional, Psicothema,” 2005
S.A.I.O. – Rectorat de Versailles, “Les logiciels d’aide à l’orientation,” 2007.
R. Chappat, “L’informatique comme aide à l’orientation, ” LE BULLETIN DE L'EPI N° 65.
T. Saaty, “The analytic hierarchy process,” McGraw Hill, New York, 1980.
J.M. TACNET, M. Batton-Hube and J. Deze, “Multicriteria decision analysis and information fusion for expertise applied to natural risks in mountains,” Colloque LambdaMu 17 –5-7, La Rochelle, France, Octobre 2010.
T. Saaty, “Some mathematical concepts of the analytic hierarchy process,” Behaviormetrika 29, 1–9, 1991.
Fouzia Ounnar, Selma Khader, Yves Dubromelle, Jean-Pierre, Prunaret, Patrick Pujo, “ Évaluation d’une méthode d’ordonnancement multicritère utilisant AHP, ”
Noorami and all, “ Comparison of AHP and FAHP for Selecting Yard Gantry Cranes in Marine Container Terminals,” Journal of the Persian Gulf (Marine Science)/Vol. 3/No. 7, 59-70, March 2012
S. Davies and N. Guppy, “Fields of study, college selectivity, and student inequalities in higher education,” Social Forces, 75 (4), 1417–1438, 1997.
J. C. Simpson, “Segregated by subject: racial differences in the factors influencing academic major between European Americans, Asian Americans, and African, Hispanic, and native Americans, ” Journal of Higher Education, 72(1), 63–100, 2001.
K.M. Galotti and Making “a Major real-life decision: college students choosing an academic major,” Journal of Educational Psychology, 91(2), 379–387, 1999.
C. A. Coperthwaite, “The effect of self-esteem, locus of control, and background factors on college students’ choice of an academic major,” Unpublished doctoral dissertation, The University of Connecticut, Connecticut, USA, 1994.
N. E. Betz, and P. J. Rottinghaus, Current research on parallel measures of interests and confidence for basic dimensions of vocational activity,” Journal of Career Assessment, 14(1), 56–76, 2006.
J. W. Lounsbury, R. M. Smith, J. J. Levy, F. T. Leon and L. W. Gibson, “Personality characteristics of business majors as de fined by the Big Five and narrow personality traits, ” Journal of Education for Business, 84(4), 200–206, 2009.
K. Leppel, “Race, Hispanic ethnicity, and the future of the college business major in the United Sates,” Journal of Education for Business, 76(4), 209–215, 2001.
N. C. Ware, N. A. Steckler, and J. Leserman, “Undergraduate woman: who chooses a science major?,” Journal of Higher Education, 56(1), 73–84, 1985.
D. Guglielmi, F. Fraccaroli and M. L. Pombeni, “The Professional Interests According to Holland’s Hexagonal Model Structures and Gender Difference, ” OSP, 33/3|2004, p. 409-427, 2004
B. Stevanovic and N. Mosconi, “ Les représentations des métiers des adolescent(e-s) scolarisé(e-s) dans l’enseignement secondaire, ” Revue française de pédagogie [En ligne], 161 | octobre-décembre 2007.
M. Lisa Larson, J. Patrick Rottinghaus, and F. H. Borgen, “Meta-analyses of Big Six Interests and Big Five Personality Factors, "Journal of Vocational Behavior 61, 217–239 (2002).
L. R. Goldberg, “An alternative description of personality: The Big-Five factor structure,” Journal of Personality and Social Psychology, 59, 1216–1229, 1990.
M. Ziegler, D. Bensch, U. Maaß, V. Schult, M. Vogel and M. Bühner, “ Big Five facets as predictor of job training performance: The role of specific job demands", Learning and individual Differences 29 1-7, (2014)
Essaid, E., Abdellah, A., & Mohamed, E. A funnel model for educational and vocational guidance in using AHP method, 3rd GLOBAL CONFERENCE ON COMPUTER SCIENCE, SOFTWARE, NETWORKS AND ENGINEERING, Istanbul Aydın University, Istanbul, Turkey, 19 – 21 November 2015
Amadou, D., Abdellah, A., & Mohamed, E. “The Choice of the Best Proposal in Tendering with AHP Method: Case of Procurement of IT Master Plan’s Realization”, I.J. Information Technology and Computer Science, 2015, 12, 1-11

Еще

Статья научная