Ускорение магнитосферных ионов вверх осцилляторной составляющей центробежной силы

В свое время Лундин и Хулквист [Lundin, Hultqvist, 1989] предложили механизм, названный ими «mag-netic moment pumping», или сокращенно MMP, предположительно обеспечивающий ускорение вверх ионов, в особенности ионов кислорода O+, и вынос их на периферию магнитосферы (см. также статьи [Lundin, Eliasson, 1991; Hultqvist, 1996, 1999; Gug-lielmi, Lundin, 2001] и обзор [Lundin, Guglielmi, 2006]). Идея [Lundin, Hultqvist, 1989] состоит в том, что под влиянием флуктуаций электрического поля ион приобретает эффективный диамагнитный момент, взаимодействие которого с магнитным полем приводит к ускорению иона, причем соответствующая сила (следуя [Guglielmi, Lundin, 2001; Lundin, Gug-lielmi, 2006], мы будем называть ее силой Лундина– Хулквиста) всегда направлена вдоль геомагнитных силовых линий в сторону уменьшения величины магнитного поля, т. е. почти вертикально вверх, если говорить о высоких геомагнитных широтах.

Непосредственным поводом для написания данной статьи послужило суждение Нильсона и др. [Nilsson et al., 2004] о том, что сила Лундина– Хулквиста служит лишь альтернативным дополнением к центробежной силе, которая обусловлена действием квазистатического электрического поля магнитосферной конвекции и является доминирующей. Напомним, что центробежная сила магнитосферной конвекции также направлена вверх (см., например, [Cladis, 1986; Horwitz et al., 1994; Demars et al., 1996]). Наша статья преследует две цели. Во-первых, мы предлагаем оригинальный взгляд на силу Лундина–Хулквиста как на колебательную составляющую центробежной силы. Во-вторых, пользуясь этим новым представлением, мы хотим подвергнуть сомнению справедливость суждения [Nilsson et al., 2004], а именно, мы приведем аргументы в пользу того, что центробежная сила, возникающая под действием колебаний электрического поля, может быть вполне сопоставима с центробежной силой, возникающей под действием среднего электрического поля магнитосферной конвекции. Сила Лундина–Хулквиста может даже заметно превышать центробежную силу магнитосферной конвекции при возбуждении в магнитосфере мощных пульсаций — так называемых глобальных Рс5 [Potapov et al., 2006; Потапов, 2008].

Сила Лундина – Хулквиста как центробеж ная сила

В рамках теории MMP [Lundin, Hultqvist, 1989] выражение для продольной компоненты силы F׀׀ , действующей на ион, было выведено в два этапа путем следующих эвристических рассуждений. На первом этапе внешнее магнитное поле B считается однородным и с помощью линеаризованного уравнения движения подсчитывается эффективный магнитный момент иона ц = mv^ / 2B, индуцированный переменным электрическим полем E(t) (см. левую часть рис. 1). Здесь m - масса иона, v± - его поперечная скорость. Предполагается, что поля E и B взаимно перпендикулярны. При вычислении ц производится усреднение по характерному периоду осцилляций электрического поля, причем считается, что данный период много больше гиропериода иона. Это приводит к соотношению ц ^ E2. На втором эта- пе принимается во внимание неоднородность геомагнитного поля B и выводится выражение для силы

F =

mc- ( E 1 v в

2 B ( B ) ¹¹

описывающей взаимодействие эффективного магнитного момента ц с неоднородным полем. Здесь c -скорость света, V,, = B ^-1 B • V .

Мы предлагаем вывод формулы (1), основанный на другой идеологии. С самого начала мы учтем, что геомагнитное поле неоднородно, и в рамках простой модели покажем, что силу Лундина–Хулквиста можно рассматривать как центробежную силу.

Пусть постоянное магнитное и переменное электрическое поля имеют вид B =(0, B y ( y , z ), B z ( z )) и E =( E x ( t ), 0, 0). Здесь E ± B , как и в модели MMP, но неоднородность поля B явно учтена с самого начала. Квазивертикальные линии в правой части рис. 1 изображают силовые линии магнитного поля. Электрическое поле направлено перпендикулярно плоскости рисунка. В верхней части рисунка показана ориентация координатных осей. Мы будем анализировать движение заряда в малой окрестности оси Z, так что | в_у | ^ | B z | и |B| ~ | B z |. Так как поле B соленоидальное ( V - B =0), B y = - y V || B . Здесь B ( z )= B z ( z ),

V|| = d I dz . Следовательно,

B x = 0, B y =- ydB I dz , B z = B ( z ), E x = E ( t ), E y = 0, E z = 0.

Теперь рассмотрим движение иона в поле указанной конфигурации. Чтобы упростить картину движения, устраним электрическое поле путем перехода в систему отсчета, движущуюся с некоторой скоростью V . В новой системе при E ^ B , V ^ c магнитное поле не изменится, а электрическое поле равно E = c B X V .

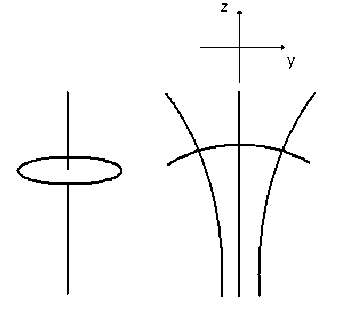
Рис . 1. Два взгляда на происхождение силы , возни кающей в магнитосфере при наличии колебаний элек трического поля и выталкивающей ионы вверх вдоль гео магнитных силовых линий ( схематическое изображение ).

Приравнивая эту величину нулю, получим дрейфовую скорость V = ( c I B ² ) E x B , что можно было, вообще говоря, предвидеть заранее. Квазигоризон-тальная линия в правой части рис. 1 показывает траекторию электрического дрейфа. Радиус кривизны электрического дрейфа, очевидно, равен R = - ( V ^ In B ) ^{- 1}. Новая система отсчета является неинерциальной, так как она вращается с угловой скоростью 65 = V I R . Центробежное ускорение R 6 ² квадратично зависит от E_x ( t ). Пусть, например, E x = E cos to t . При условии 6 <  ^ , где Q - гирочастота иона, осциллирующее вращение системы отсчета вполне согласовано с движением иона поперек магнитных силовых линий. Центробежная сила, действующая на частицу, равна mR 6) ² или

- m ( cE_x IB ) ² V | in B . (3)

После усреднения этой величины по периоду осцилляций электрического поля мы получаем выражение для силы mc2 ( E12

F i =-            v,| in b ,

1      2 (B) 1

совпадающее с (1). Другими словами, силу Лундина– Хулквиста действительно можно рассматривать как колебательную составляющую центробежной силы.

Сопоставление усредненной и колебательной составляющих центробежного ускорения

Итак, мы имеем две составляющие центробежной силы, действующей на ионы в магнитосфере Земли. Одна из них связана с осцилляциями электрического поля и описывается формулой (4). Другая составляющая связана с усредненным крупномасштабным электрическим полем магнитосферной конвекции. Это поле мы обозначим как E _c , а соответствующую силу, ускоряющую ионы вдоль геомагнитных силовых линий, как F ^ . Выражение для

F lc в рамках дрейфовой теории имеет вид

F ^c =- m V d ! .

^{1 c} dt

Здесь т = B I B – единичный вектор, касательный к силовой линии магнитного поля, V _c = ( c IB ) E _c X т -скорость электрического дрейфа (см. например [Морозов, Соловьев, 1963; Cladis, 1986; Horwitz et al., 1994]). В статическом магнитном поле

-= w + ( V c V ) т ,                 (6)

dt где V| — продольная проекция скорости ведущего центра. Используем такую же конфигурацию электромагнитного поля, как и при выводе формулы (4), с заменой E на Ec. Тогда из (5), (6) следует

( E. 1 ²

F i = - mc ²    - V„ in B .

1 I B ) 1

Мы видим, что формула для F отличается от (4) отсутствием коэффициента 1/2 в правой части. Таким образом, колебательная составляющая силы меньше или больше усредненной, если E меньше или больше 2 E _c . Вообще говоря, априори возможны обе ситуации. Поэтому обратимся к результатам измерений и расчетов электрических полей в магнитосфере.

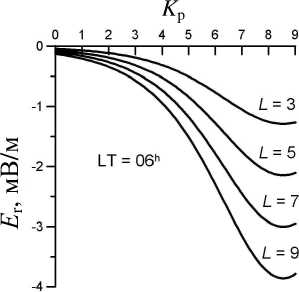
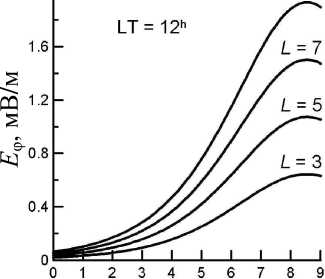
Крупномасштабное электрическое поле конвекции в магнитосфере направлено с утренней стороны на вечернюю, обеспечивая поток плазмы из геомагнитного хвоста в солнечном направлении. О его существовании было известно задолго до того, как его удалось измерить. Существуют модели, описывающие это поле. Одна из наиболее известных – это модель Волланда [Volland, 1973], позднее уточненная в работе [Maynard, Chen, 1975]. На рис. 2 показаны следующие из этой модели зависимости радиальной и азимутальной компонент электрического поля от K _р -индекса и расстояния в экваториальной плоскости для двух меридианов – утреннего и полуденного. Обе составляющие зависят также от азимутального угла φ, отсчитываемого от полуночного меридиана против часовой стрелки. Радиальная компонента пропорциональна sinφ, а азимутальная – cosφ.

Реально измеренные значения электрических полей в магнитосфере могут сильно отличаться от предсказываемых моделью, особенно во время суббуревых возмущений. В настоящее время для измерения электрических полей in situ используется несколько методов. Для квазистационарных и низкочастотных полей наиболее употребительными являются метод двойного зонда [Pedersen et al., 1998] и

2Г                     L = 9

K p

Рис . 2. Радиальная компонента электрического поля конвекции в экваториальной плоскости вдоль утреннего меридиана ( а ) и азимутальная компонента электрического поля конвекции в экваториальной плоскости вдоль по луденного меридиана ( б ) в зависимости от K _р - индекса и L - параметра .

метод измерения дрейфа электронов [Paschmann et al., 1998]. Поскольку оба способа измеряют электрические поля в диапазоне от нуля до сотен герц или нескольких килогерц , то для сравнения одновременных значений квазистационарных полей (к которым относится электрическое поле конвекции) и полей УНЧ-колебаний лучше всего использовать прямые измерения на спутниках. Примером могут служить наблюдения с помощью прибора EFI (electric field instrument) на спутниках THEMIS [Bonnel et al., 2008]. EFI использует разновидность метода двойного зонда и имеет частотный диапазон от 0 до 4 кГц.

В работе [Sarris et al., 2009] приведены результаты наблюдений электрического и магнитного поля геомагнитных пульсаций типа Рс5 с помощью приборов EFI и феррозондовых магнитометров, установленных на группе спутников THEMIS. На рис. 2 этой работы показано событие 4 сентября 2007 г. В период с 04:00 до 08:42 UT спутник THEMIS-D двигался между магнитными облочками L =4 и L =10 в пред-полуденном секторе магнитосферы недалеко от экваториальной плоскости (наклонение орбиты 16º). В 08:42 UT он пересек магнитопаузу. Из приведенных [Sarris et al., 2009] осциллограмм вариаций электрического поля видно, что поведение компонент ква-зистационарного поля в целом соответствует ожидаемому из модели Волланда поведению поля конвекции. Радиальная квазистационарная компонента имеет отрицательное значение и меняется в пределах от –4 до 0 мВ/м. Азимутальная составляющая положительна, после выброса она падает с 5 до 3 мВ/м и остается на этом уровне, незначительно варьируя, до пересечения магнитопаузы . Величина обеих компонент поля конвекции превышает предсказываемую моделью , если учесть, что индекс K _р в течение всего периода измерений имел значение 2 _– . Однако это могло быть связано с тем, что скорость солнечного ветра была высокой и медленно спадала с 650 до 600 км/с.

Что касается геомагнитных пульсаций Рс5, то, если судить по приведенной на том же рисунке работы [Sarris et al., 2009] осциллограмме магнитных колебаний, они имели в магнитном поле умеренную амплитуду, не превышающую 2 нТл. На земле в это же время Рс5 наблюдались на цепочке скандинавских магнитометрических станций IMAGE и также имели небольшую амплитуду с максимумом примерно 10 нТл на геомагнитной широте 71º. (Для сравнения: во время небольшого магнитного возмущения утром 28 октября 1991 г. амплитуда Рс5 превышала на той же станции 100 нТл. На рис. 3 два события показаны в виде осциллограмм x-компоненты магнитного поля.) В электрическом поле, как свидетельствуют те же спутниковые измерения, интенсивность Рс5 существенно превышала величину квазистационарного электрического поля, основу которого, по всей видимости, составляло поле конвекции. По радиальной компоненте амплитуда составляла от 3 мВ/м в середине интервала до 4.5 мВ/м ближе к магнитопаузе. Азимутальная составляющая имела размах около 5 мВ/м. Итак, в данном событии амплитуда волнового поля была примерно в 1.5 раза выше значения стационарного поля. При этом надо учесть, что колебания Рс5 не были глобальными, так как по данным сети IMAGE они наблюдались лишь на высоких широтах.

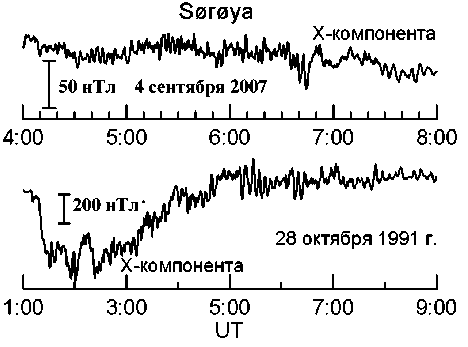
Рис . 3. Осциллограмма вариаций магнитного поля , наблюдавшихся во время события 4 сентября 2007 г . на обс . Sørøya ( верхняя панель ), и пример другого собы тия Рс 5, наблюдавшегося во время небольшого возму щения ( D _st ≈ –70 нТл ) на той же обсерватории 28 октяб ря 1991 г . ( нижняя панель ).

Еще более яркий пример превышения значения электрического поля конвекции амплитудой УНЧ-ко-лебаний приведен в работе [Liu et al., 2009] на рис. 2, правая панель. Спутник находился в околополуден-ном секторе. Стационарное поле в соответствии с моделью Волланда имело близкую нулю радиальную составляющую и небольшую, не более 2 мВ/м, азимутальную компоненту. Амплитуда колебаний Рс5 при этом составляла около 4 мВ/м по радиальной составляющей и около 3 мВ/м по азимутальной.

Таким образом, обзор имеющихся в литературе измерений электрических полей позволяет заключить, что в магнитосфере достаточно обычны ситуации, когда интенсивность волновых полей с частотой от одного до нескольких миллигерц превышает в 2–3 раза величину электрического поля конвекции.

Обсуждение

В предыдущих разделах статьи мы показали общность силы Лундина–Хулквиста и центробежной силы магнитосферной конвекции. Обе они ускоряют ионы вверх вдоль геомагнитных силовых линий, описываются аналогичными формулами (см. формулы (4), (7)) и, вообще говоря, вполне сопоставимы по величине. В данном разделе мы укажем на различие между осцилляторной и усредненной составляющими центробежной силы.

Важнейшей особенностью магнитосферной конвекции является ее перманентность. Крупномасштабная конвекция в магнитосфере испытывает вариации во времени, но происходит постоянно, коль скоро магнитосфера постоянно взаимодействует с непрерывно дующим солнечным ветром. Поэтому соответствующая компонента центробежной силы постоянно ускоряет ионы вверх, перенося их с ионосферных высот на периферию магнитосферы [Cladis, 1986; Horwitz et al., 1994]. В этом отношении она отличается от осцилляторной составляющей, которая определяется весьма изменчивым режимом пульсаций магнитосферы. Разумеется, и это хорошо известно, в магнитосфере существуют перманентные пульсации. Они зарождаются в солнечном ветре перед фронтом околоземной ударной волны, проникают в магнитосферу и наблюдаются на земной поверхности в виде дневных устойчивых пульсаций Рс3 [Потапов, 1974]. Однако амплитуда Рс3 относительно невелика, так что связанная с ними осцилля-торная составляющая центробежной силы не может конкурировать с центробежной силой магнитосферной конвекции. Иное дело мощные глобальные пульсации Рс5, о которых говорилось в предыдущем разделе, но эти пульсации возникают в магнитосфере спорадически. Таким образом, механизм ускорения ионов осцилляторной составляющей центробежной силы, по-видимому, следует рассматривать как важный дополнительный механизм, который включается спорадически при возбуждении в магнитосфере глобальных Рс5.

Заключение

В данной работе показано, что механизм ускорения ионов вверх под действием колебаний электрического поля, предложенный Лундиным и Хулкви-стом [Lundin and Hultkvist, 1989] и известный ранее как MMP, или накачка магнитного момента, можно рассматривать как механизм центробежного ускорения. Если говорить более точно, то речь идет об ос-цилляторной составляющей центробежного ускорения. В этом контексте естественно возникает вопрос о сопоставлении MMP с центробежным ускорением, обусловленным квазистатическим полем магнитосферной конвекции. В рамках простой модели показано, что на высоких геомагнитных широтах колебательная составляющая центробежной силы меньше или больше центробежной силы магнитосферной конвекции, если отношение амплитуды колебаний электрического поля к среднему полю соответственно меньше или больше 2 . Анализ данных измерений и расчетов электрических полей в магнитосфере свидетельствует о том, что осцилляторная составляющая центробежной силы может быть сопоставима с центробежной силой магнитосферной конвекции и даже превосходить ее при возбуждении в магнитосфере мощных пульсаций типа глобальных Рс5, вопреки мнению, которое высказывалось в литературе по данному вопросу.

Выражаем искреннюю благодарность Б.И. Клайну, Р. Лундину и Х. Нильсону за обсуждение проблемы ускорения ионов в магнитосфере. Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (гранты 0905-00048, 10-05-00661).