Условие экстремальности поверхности вращения для функционала типа площади

Пусть Q — ограниченная область в R ³ , M С Q — заданная C ² поверхность, S = д^ — граница Q. Предположим, что в R ³ определены неотрицательные C 2 -функции а(х) и ©x). Определим два функционала, выражаемые интегралами [3]

J i ( m ) = У

S

a( | x | )dS,

J 2

^{( M} ’=/

Ω

где x = (x 1 ,x ₂ ,x ₃ ), dS — элемент площади. Поставим перед собой задачу исследования поверхностей вращения M, являющихся экстремалями функционала

J(M ) = J 1 (M ) - AJ 2 (M ).

К такому функционалу приводит задача минимизации функционала весовой площади J 1 (M ) при условии, что пространственный функционал J 2 (M ) = const. В частности, в теории капиллярных поверхностей [1] исследуется задача минимизации открытой площади поверхности при условии несжимаемости, то есть при постоянном объеме жидкости.

1.    Формула функционала для поверхностей вращения

Рассмотрим поверхность M , заданную вращением вокруг оси x 3 графика функции, определяемой уравнением р = p(t), где р — расстояние точки P до оси t (рис. 1). Примем за параметры точки P величину t и полярный угол θ . Для определенности будем считать, что t принадлежит некоторому числовому отрезку (a, b), а 6 изменяется от 0 до 2п, функция р = p(t) определяет форму меридиана. Имеем

r(t, 6) = { p(t) cos 6, p(t) sin 6, t } , r _t = { p ' cos 6, p sin 6,1 } , r o = {-p sin 6,p cos 6, 0 } .

Поэтому коэффициенты первой квадратичной формы поверхности примут вид E = (r t ,r t ) = p 0 2 + 1, F = (r t ,r e ) = 0, G = (r _e ,r _e ) = p ² .

Тем самым dS2 = (p02 + 1)dt2 + p2d6'2.

Рис. 1

Далее получим

2π      b

J1(M) = I a(|x|)dS = J d6 J apEG - F2dt где a = a(p(t)).

b 2π ρ

J 2 (M) = I ^( | x | )dx = I dt I d6 I _Vpdp

b

= 2п У appp'² + 1 dt,

a

b

= 2n J h(p(t))dt,

a

где ^ = ^(p(t)) и

ρ

А(р) = /

v ⁽ y)ydy.

Вариационная задача для рассматриваемого функционала формулируется следующим образом. Среди всех поверхностей вращения M с фиксированным значением пространственного функционала J ₂ (M ), определяемых функциями p(t), имеющих непрерывную производную и удовлетворяющих граничным условиям

P(a) = A, P(b) = B, найти ту из них, которая доставляет слабый экстремум функционалу J1 (M). Из вариационного исчисления известно, что решения такой задачи являются экстремалями функционала J(M) = J1(M) — AJ2(M). В терминах функции p(t) мы, тем самым, получаем следующий одномерный функционал

b

J [p(t)] = У (аррр² + 1 — A + h(p))dt.

a

Поскольку данный функционал не зависит явно от t, так что F = F(р,р'), следовательно уравнение Эйлера — Лагранжа [2] можно записать в следующем виде d (F — p’Fpo )=0.

То есть d dt

арр р² + 1 — Ah(p) —

арр2

Рр² + 1

Введем обозначение р = и. Тогда первый интеграл выше приведенного уравнения примет вид

a(u)uVU'2 + T — Ah(u) — •      ' = д и'2 + 1

или

а(и)и

V u ' ² + 1

— Ah(u) = д.

Здесь д = const. Откуда

/ а(и)и     ²

и ² = I ------------ )

д + Ah(u)

— 1 .

Разделение переменных дает dt = ±

du

^aWu А у У ^ + Xh ( u )

-

Откуда интегрированием получим t=±/

du

^{a ( u )} u A у У р + ХЦи )

+ C.

-

Таким образом, имеем общее решение уравнения Эйлера — Лагранжа с постоянными интегрирования µ и C .

Теорема 1. Пусть M с Q С R3 — заданная поверхность вращения, а t=±/

du

o(u)_u у у ^+Ah(u)

+ C —

-

решение уравнения Эйлера — Лагранжа (2) для функционала типа площади (1). Тогда заданная поверхность M является экстремальной.

2.    Примеры

Пример 1. Положим в рассмотренной выше вариационной задаче а(р) = 1, ^(р) = 0.

Тогда наш функционал примет вид

b

J \р(€)\ =

j ррр² + 1 dt.

a

Полученный выше интеграл (4) дает следующее общее решение t=±

du

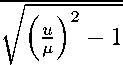
+ C = ц arch —+ C.

µ

Тогда график функции

А ( t - C ^ р = u = ц ch

µ

представляет собой цепную линию, а соответствующая ей поверхность вращения — минимальная поверхность — катеноид.

Пример 2. Пусть теперь а(р) = и 2, ^(р) = 0. Будем рассматривать функционал

b

J [р(t)] = У ^ 1р р р ⁰² + 1 dt.

a

Получим общее решение

t =

/

du

+ с.

µ ² u

- 1

Откуда заменой 1/^2 = k, u = кт, т = sin2 2 приходим к виду t =

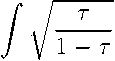
dт + C =

1/(1

— cos 6)d6 + C = 2 (6 — sin 6) + C.

Тогда графиком функции

θ p = u = к sin ^

k

= ^ ⁽¹ - ^{cos 6 )}

является циклоида.

3.    Симметричность решения вариационной задачи

В простейшем случае рассматриваемая задача на экстремум представляет собой хорошо известную изопериметрическую задачу о минимуме площади замкнутой поверхности среди всех поверхностей, ограничивающих область фиксированного объема. Другими словами, a(p) = ^(p) = 1. Известно, что решением этой задачи является сфера, имеющая плоскость симметрии, проходящую через ее центр. В нашем случае для поверхностей вращения следует ожидать существования аналогичного свойства, которое формулируется в следующей теореме.

Теорема 2. Пусть p(t) является решением уравнения (2) и пусть точка t o Е (a, b) является точкой локального минимума или локального максимума. Тогда график этой функции симметричен относительно прямой t = t ₀ в любой окрестности этой точки, не содержащей других точек экстремума.

Доказательство. Не ограничивая общности, будем считать, что t ₀ = 0 — точка локального минимума, так, что при t >  0 функция p(t) возрастает, а при t <  0 — убывает. Введем обозначение

F^{( u )} =

^{a ( u ) u} А у У ^+Ah(u)

-

Тогда уравнение (3) перепишется в виде u02 = F 2(u).

Рассмотрим две симметричные точки t1 = т, t2 = —т, где т > 0. Пусть u1 = u(ti), u2 = u(t2), u0 = u(0). Тогда имеем u1

j F(z)dz = t1 = т, u0

и

u 0

j F(z)dz = — 1 ₂ = т.

u 2

Вычитая эти равенства, приходим к u2

IF(z)dz = 0, u1

что в силу положительности функции F(u) означает: u 1 = u₂. Это доказывает симметричность графика решения уравнения (2).