Условия действия и ограниченности операторов внутренней суперпозиции с весом в пространстве функций на полуоси
Автор: Симонов П.М., Чистяков А.В.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Математика
Статья в выпуске: 1 (36), 2017 года.
Бесплатный доступ
Доказаны утверждения об условиях действия и ограниченности операторов внутренней суперпозиции с весом в пространстве функций на полуоси.
Функциональный оператор, функционально-дифференциальный оператор, оператор внутренней суперпозиции с весом, оператор подстановки с весом, условие "независания "
Короткий адрес: https://sciup.org/14730095
IDR: 14730095 | УДК: 517.929 | DOI: 10.17072/1993-0550-2017-1-5-12
Текст научной статьи Условия действия и ограниченности операторов внутренней суперпозиции с весом в пространстве функций на полуоси
В статье рассматриваются линейные операторы S и T , входящие в линейные функционально-дифференциальные уравне ния вида nm
X ( t ) = £( S i X )( t )+^( j )( t )+ f ( t ), t >0, (1)
i =1 j =1
где x ( t ) - неизвестная функция из заданного пространства D функций на множестве [0, ос), f (t) - заданная функция из пространства B функций, определенных на множестве [0,ос). Исследование основано на изучении свойств операторов, заданных левой частью уравнения (1). Такие линейные операторы в дальнейшем будем называть: операторы S – функциональными, операторы T – функционально-дифференциальными.
Основное внимание для уравнения (1) уделяется исследованию спектральных свойств, в первую очередь обратимости и нё-теровости [5, 10]. Также важно исследование ограниченности и действия операторов S и T в задачах устойчивости [1–4].
Класс операторов S и T весьма широк и его отдельные представители связаны с задачами из различных областей математики и ее приложений. Среди таких областей можно указать, кроме классической теории функциональных уравнений, теорию функционально-дифференциальных уравнений с отклоняющимся аргументом, теорию дифференциально-функциональных уравнений "нейтрального типа", теорию нелокальных задач для уравнений с частными производными, теорию краевых задач для уравнения колебаний струны и уравнений смешанного типа, ряд вопросов общей теории операторных алгебр и теории динамических систем,
спектральную теорию автоморфизмов банаховых алгебр и другие вопросы.
Обозначения и определения
Пусть L - линейное пространство измеримых и локально суммируемых функций f :[0, да) ^ I”, D - линейное пространство локально абсолютно непрерывных функций x :[0, да) ^ Ж”, производные которых принадлежат пространству L. Здесь и ниже Ж” -линейное пространство вещественных векторов-столбцов с нормой | • |. Будем предпола гать, что норма | • | ” х ” -матрицы согласова на с нормой в Ж”.
Обозначим
L p
.. .. (да Уp
V €L :|fL = f | f (')|pdt p k 0 J
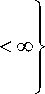
при 1 < p <да и
L да- { f € L : || f I L E vraisup| f ( ' ) |< да } .
Для 1 < p <да и 1 < r <да введем пространства Lpr функций f € L [1; 10, с. 17] таких, что
L да r 4 f € L ji f L r - sup]4Д <4.
^ i £ 0, да r
Очевидно, что Lpr c L^ при любых 1 < p , r <да . Кроме того, пространства Lpp и Lp совпадают по запасу элементов и их нормы при этом равны.
Символом C обозначим пространство непрерывных функций у :[0, да ) ^ Ж ” , а BC - пространство функций у € C , для которых
II y|Bc - sup| у ( t ) | <да - t > 0
И, наконец, при 1 < p < да , обозначим
W P - DL p -
-
- { x € D : x € L p , X € Lp ; I| x||dlp -1 x L +1 x L } .
Нетрудно показать, что DLp c BC, причем это вложение непрерывно.
Для любого элемента x € DLp верно представление x = Wf + Ua . Здесь f = X + x, f € Lp, a = x(0), a € Ж”. Оператор W опре- деляется равенством t
(Wf )( t ) = f e s - ' f ( s ) ds , 0
оператор U определяется равенством (U a) (t ) = e - ' a .
Введем также весовые пространства: L gp ( p = 1,oo, gE Ж) - пространство всех таких измеримых функций f : [0, ос) —> Ж ” , каждая из которых представима в виде f ( t ) = eYg ( t ) , где g € Lp , с нормой || f || L g - || g HL . Аналогично введем пространства
тr Lpr •
Действие и ограниченность функционального оператора
Рассмотрим оператор внутренней суперпозиции с весом (оператор подстановки с весом) [6, с. 19]:
( Sy )( t ) = G ( t ) у ( g ( t )) , ' >0.
Здесь элементы ”X” -матрицы G измеримы и локально суммируемые, а измеримая функция g(t):[0,оо)^Ж удовлетворяет условию "независания" [6, с. 18] или условию согласования [5, с. 31]: если n С[0,оо), то mesn = 0^ mesg-1(n) = 0 , где mes - мера Лебега.
Изучим условия действия и ограниченность из пространства L в пространство Lp (1 < p < да).
Будем предполагать, что если g ( t ) <0 , то G ( t ) = 0 . Следуя [8, 9] обозначим при 1 < p < да функцию
G* ( t ) = lim vraisup | G ( t ) | p me^° t eg -1 ( e )
mes g '( e )
mes e
Лемма. Пусть z € Lp , 1 < p < да ,
2 > 0, - +1 = 1.
pq
Тогда
X J
a:
n + 1
e — A ( n — s )
n = 0
eA
A p 1 - e ’ “
z 1 - e
ap A
z
^g
g
2 "Ip A p
L
Доказательство
Пусть p > 1 . Тогда получаем:
a
n + 1
p
<
= e A q
2 A P
I ^q) I
1 - e
1 x - 1 Ap \
► 2
p
Пусть p = 1 , тогда вычисляем: a n + 1
XJ e - A("-”1-- ( n=0 0
a n k + 1
= xxJ e ■-n -4
n = 0 k = 0 k
Is =
X J
n = 0
e — A ( n - s )
a
= X e-Apn n=0
n+1 P j eAs |z(s)| ds
. 0 J
(неравенство Гёльдера)
<X e - ap'
n = 0
f n + 1 A gs
p q n+1 Aps
<
к 0
a
= X e-APn n=0
Aq
p Aq ( n + 1)
e
z
—
p
.
n + 1 A ps
• J e 2 | z ( s )| P ds <
Aq A 2 e 2
A q
A q
2 e T
Aq
p
q
» n +1 - Ap , „
X J e 2 |z(s)|P ds = n=0 0
p q
a n k + 1 k p. .
XX J e - A " - ' '
n = 0 k = 0
k
A q
2 e T
p q
a
n
Aq
A q
2 e T
p q
Aq
e
XX e
n = 0 k = 0
k + 1
Ap( t nk + 1
■ - ( n - k - 1) J \z ( s )| Pds <
k
^ p -
'2 ' X J l z ( s ) ds ’ X e
k = 0 k
n = k
к A q )
p
q X
n = 0
A P —
1 - e 2
- Ap ( n - k )
<
k + 1
■ J | z ( s )| p ds =
k
a n XX e -A ( n = 0 k = 0
a k + 1
k + 1 : n - k - 1) f
k
= e
k = 0 k
X e - A ( n - k ) = n = k
Z, A
= . I HL,.
Таким образом, получаем:
r ( A ) = J c P
e A
1 - e
A , P = 1,
e A
A p —
1 - e 2
A P — 2(1 - e 2)
1 q
Aq
, 1 < p < a .
Утверждение A. Оператор S действует и ограничен из пространства L в пространство Lp (1 < p < a ) тогда и только
тогда, когда
При этом
GPg£L~ .
( A)
11
S\\^Lp
.
Доказательство. Ограничимся для простоты скалярным случаем.
Если g удовлетворяет условию "независания", то справедлива формула замены переменной в интеграле [11, с. 577]. Отсюда
ll Sy ll P = [ l G ( t )l P -l У ( g ( t ))l pdt = p
= JGPp ( t )l У ( t )l Pdt<
< ll GPg ll l^ 'll У ll P .
Необходимость (A) и выражение для нормы есть в [5, 7–9, 13].
Утверждение B. Оператор S действует и ограничен из пространства L в
пространство L тогда и только тогда, когда
и
G e L „ ( B ) .
При этом || S || l^ <|| G ||.
Доказательство (см. [5, 7–9, 13])
Утверждение C. Оператор S действует и ограничен из пространства L в пространство L ( r ≠ ∞ ) тогда и только
е мк g g ^(Д m )П Д к , m ( в мк )>0
G g ( t ) > g Mk - ye^ M^ для любого t e eMk .
Определим
У м ( t )= X ' ■ X.., ( t ) .
к=M ^ ( . мк ) м к
Несложно проверить, что || yM HL =1.
тогда, когда
K = sup[^ vrai sup G r ]V r < °°- ( C )
m k = mg~ 1 ([ m , m+ 1])П[ k , k +1]
При этом ||
S\\L ,
Теперь
11 Sy M || l'
r
£ J Gg (t )| Ум (t )| rdt = к=Mg- 1(Д M ) 4
Доказательство
Обозначим Am=[ m,m + 1], m eNU0.
∞
= X 1
к = M ^ ( e Mk )
Для скалярного случая вычислим норму:
II Sy || r = sup [G r ( t >| y ( g ( t » | r dt =
Lr m
m
= sup f Gg(t >| y(t)| r dt = m g- 1(Am)
∞
* X ( g M.
K = M
≥ Kr - ε
-
f Grg (t)dt > eMk
ε ∞
9 к + 1 - M ) = X g Mk
2 к = M
- ε ≥
2 2
- = Kr - s .
= sup£ J Gg(t>■| y(t>|r dt < m k=mg-1(Дm)ПДк
< sup^ vrai sup Gh (t) • m k=mg-1( Am )П Дк
-
• / | y ( t )| r dt<
g 1 (A m )4
-
< supsup | y ( t ) | r dt •
Таким образом показано, что для любого s >0 существует такой элемент y e L x r , || y || L =1 и выполняется
неравенство || Sy || r >Kr —e.
Из последнего неравенства немедленно следует, что || S ||z _>L >K и, объединяя с rr
(C1), получим || S |L _^, = K .
LrLr
В процессе доказательства для нормы S получено, что если
£ vrai sup
G
g
к = mg- 1(Д m )П Д к r°r
Таким образом
||
S
|L
LrLr
2 vrai sup Gg(t)> AM -e, к=Mg- 1(д м )n д. 2
( C 1)
Докажем в скалярном случае равенство || S || Lp=Lp = K .
Пусть s >0 - произвольное число.
Тогда существует M = M ( s ) > 0 , такое что
J2 vrai sup Grr (t) > Kr к=Mg- 1(Д M )n Дк
e
Обозначим gM = vrai sup Gg .
к g- 1 (Д m )П Д к
Существует последовательность измеримых множеств
то существует У м e L, r : W У м W l /. = 1 такое, что 0 Sy M \txr-^Lxr> Ar M -e -
Поэтому, если sup £ vrai sup Gg (t) = oo, м K=Mg- 1(дм)nд.
то оператор S не ограничен из L в L .
Поскольку оператор S регулярный, то действие эквивалентно ограниченности (конус в L – воспроизводящий и нормальный [12 , с. 397]).
Действие и ограниченность функционально-дифференциального оператора
Рассмотрим оператор внутренней суперпозиции с весом (оператор подстановки с весом) [6, с. 19]:
( Tx )( t ) = H(t ) x ( h ( t )), t >0.
Здесь элементы nxn -матрицы H измеримы и локально суммируемые, а функция h(t) : [0,oc) -^R - измеримая.
Изучим условия действия и ограниченность из пространства DLp = Wp в пространство Lp (1 < p < ж).
Будем предполагать, что если h ( t ) < 0 , то H ( t ) = 0.
Утверждение D. Оператор T действует и ограничен из пространства DLp в пространство Lp (1 < p < ж), если и только если sup( f | H(t)|pdt)1Zp <оо. (D1)
m h- ‘ ([ m , m +1])
Доказательство
Ограничимся для простоты скалярным случаем.
Условия действия и ограниченности оператора T : DLp ^ Lp эквивалентно условиям действия и ограниченности двух операторов TU: R LLp и TW: Lp ^ Lp .
Докажем необходимость.
Тогда справедливы соотношения
+ ® > j | TU | p ( t ) dt = J | H ( t ) | p e - ph ( t ) dt =
0 0
= £ / । H (t )| p e~ph (t) dt> m=0h ‘(Am)
-
>£e- p ( m +D J । h ( t )| p d t . ( D 2)
m =0 h~ ‘ (A ,„ )
Значит, | H ( • ) | p суммируема на каждом множестве h ’( Am ) .
Далее, получаем
ОО h ( t )
|| TWz || p = J | H ( t ) | p [ Je(h ( t ) s ) | z ( s ) | ds ] p dt = 0 0
ж h ( t )
= E J | H(t)|p [ J e-(h(t)-s)| z(s)ds]pdt > m=0 h-1( Am ) 0
-
> E [ m e - m - s ) | z ( s ) ds ] p J | H ( t )| p dt >
m =0 0 h - 1 ( A m )
-
> e-p (J | z ( s )| ds ) p J | H ( t )| p dt
M -1 h- ‘ (A m )
для любого M > 1.
Или || TWz || p >
-
> e p ( J | z ( s )| p ds ) p J | H ( t )| p dt . ( D 3)
Mh~ ' (Д m ,)
Множество { z M ( s ) = X [ м - 1M ] } , где
M > 1 ограничено в L , причем || zM \\L =1 pp для любого M > 1.
Так как оператор TW = Q ограничен как оператор Lp ^ Lp , то
HTWz m || p ^| Q | p ^ .
Учитывая неравенство ( D 3) , получим, что для любого M > 1 справедливы неравенства
Г | H(t)|pdt < ep ШР^р • При M = 0 из неравенства (D 2) получим [ | H(t)|pdt p h- ‘(ДО Таким образом, если T : DLp ^ Lp, то (D1) выполнено. Докажем достаточность. Если выполнено (D1) , то || TU || p = J | (TU)(t) | pdt = f| H (t) |pWp(t) dt = 0 0 = £ / । H(t)|p e~ph(t) dt< m=0h ‘(Am) „ 1 ≤ 1 — e - - sup J |H(t)|pdt< X. m h-1(A m ) Аналогично вычисляем: oo h (t) || TWz ||p = /dt[H(t) Je(h(t)-s) | z(s) | ds]p = 0 0 h (t) ∞ = S J H (t) J e_(h(t)-s )| z (s )|ds ] p < m=0 h-1( Am ) 0 X m+1 <^[ J e —' m- ’ '|z (s )ds ] p J \H (t ^dt < m=0 0 h-1( Am ) < sup f | H (t) |p dt • m h 1(A m) •£["[e~(m-s)| z(s)|ds]p. m=0 0 использовались вложения Здесь DLp о Lp (DLp c Lp „ ) . В силу леммы || TWz ||l p m h1(A m) p Замечание. Если h удовлетворяет условию "независания", то условие (D1) эквивалентно условию sup( J Hhp (t)dt)1/p < X. m [ m, m+1] Следствие. T : DLp ^ Lp (p ^ x ), если выполнено хотя бы одно из условий: 1) если H g Lp, следует из (D1) , которое эквивалентно действию и 2) если H p∈L , то, в силу замечания, эквивалентно действию и ограниченности оператора T : Lp ^ Lp . 3) если H p∈L , то, в силу замечания, эквивалентно действию и ограниченности оператора T : L^ ^ Lp 4) ea(“h(^H(•) g L^p эквивалентно действию и ограниченности оператора αα T: LX p ' Lx p . Выведем следствие 4. Проверим условие (D1) : J | H (t) |p dt = h- 1(A m ) = £ J | h (t )| pdt = k=0 h 1(Дm )ПAk m = У Г e-ap(t-h(t)) , k =0h- 1(Дm )П At .[ea(t-h(t» | H(t) |]pdt < < ^e-a(m—k—1)J [ea(t—h(t)) | H(t) |]pdt< k=0 A k αp < sup J [e-a(t—h(t» | H(t) |]pdt • ,p< X. k Ak 1 e Утверждение E. Оператор T действует и ограничен из пространства DL в пространство L , если и только если vrai sup | H (t) |< oo. (E1) t >0 Доказательство Докажем необходимость. Рассмотрим скалярный случай. Вычисляем: || TU HL = vrai sup | H(t)e "(t) |= 00t = sup vraisup | H(t)eh(t) |>e~1 vraisup | H(t)|, m t-h- ЧД m ) t-h' 4^) откуда vraisup | H(t)| Вычисляем значение оператора на единице: HTW 1\\L =vraisup[|H(t)| 00 t >0 h (t) J e~(h(tbs) ds ] = h (t) = sup vraisup [| H(t) | [e~(h(t)_s) ds] > m teh- ЧД m ) 4 m > sup vrai sup [| H(t) | Pe(m s) ds] > m t-T m ) 0 > (1 — eM) vraisup | H(t)|, t-h~1(A m ) откуда vraisup | H(t)|<'У|| TW 1||l , при M >1.(E3) t-h-1(Am ) e ~ Из (E 2) и (E 3) следует (E1). Докажем достаточность. Неравенство очевидно: 11 TU |\L< vrai sup | H(t) |< oo. 00 t >0 Вычисляем: h (t) || TWz\\L = vraisup[| H(t) | Гe~(h(tbs) | z(s) |ds] < “ t>0 J t < vraisup|H(t) |sup fe(' s) | z(s) |ds < t>0 t>0 “ < vraisup| H(t)|-|| W ||l B. -|| z ||l • t >o x x Утверждение F. Оператор T действует и ограничен из пространства DL (при 1 < г < ос) в пространство Lmr, если и только если ' m+1 1г m Доказательство Докажем необходимость. Вычислим: II TU\\L =sup J [|H (t )| e-h(t)\dt = mm m m k~0 \m h 1(^k) sup £e-r(k+1) f \H (t )| rd m k°' A.nh-1(Дк ) e г sup £ Г \H(t)|rdt = m k 0 m k 1( Ak ) = e гsup J mm отсюда m m Докажем достаточность: IITU\\L =sup ^H(t)|r e^h(t)dt r m r m m < sup r t *0 0 < sup m m 1 r IL^BC II Lr • Заключение Результаты этой статьи дают полные доказательства утверждений 1, 3 и следствие 1 из статьи [1].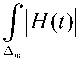
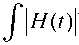
Список литературы Условия действия и ограниченности операторов внутренней суперпозиции с весом в пространстве функций на полуоси
- Азбелев Н.В., Березанский Л.М., Симонов П.М., Чистяков А.В. Устойчивость линейных систем с последействием. I//Дифференциальные уравнения. 1987. Т. 23, № 5. С. 745754.
- Азбелев Н.В., Березанский Л.М., Симонов П.М., Чистяков А.В. Устойчивость линейных систем с последействием. II//Дифференциальные уравнения. 1991. Т. 27, № 4. С. 555-562.
- Азбелев Н.В., Березанский Л.М., Симонов П.М., Чистяков А.В. Устойчивость линейных систем с последействием. III//Дифференциальные уравнения. 1991. Т. 27, № 190. С. 1659-1668.
- Азбелев Н.В., Березанский Л.М., Симонов П.М., Чистяков А.В. Устойчивость линейных систем с последействием. IV//Дифференциальные уравнения. 1993. Т. 29, № 2. С. 196-204.
- Антоневич А.Б. Линейные функциональные уравнения: Операторный подход. Мн.: Университетское, 1988. 232 с.
- Бухвалов А.В. Порядково ограниченные операторы в векторных решетках и пространствах измеримых функций//Математический анализ. Т. 26. Итоги науки и техн. ВИНИТИ АН СССР. М.: ВИНИТИ, 1988. С. 3-63.
- Драхлин М.Е., Плышевская Т.К. Действие оператора внутренней суперпозиции в лебеговых пространствах//Краевые задачи: межвуз. сб. науч. тр. Пермь: Перм. политех. ин-т, 1980. С. 158-165.
- Драхлин М.Е. Об одном линейном функциональном уравнении//Функционально-дифференциальные уравнения. Пермь, Перм. политех. ин-т, 1985. С. 91-111.
- Драхлин М.Е. Оператор внутренней суперпозиции в пространствах суммируемых функций//Известия вузов. Математика. 1986. № 5. С. 18-24.
- Курбатов В.Г. Линейные дифференциально-разностные уравнения. Воронеж: Изд-во ВГУ, 1990. 168 с.
- Макаров Б.М., Подкорытов А.Н. Лекции по вещественному анализу: учебник. СПб.: БХВ-Петербург, 2011. 668 с.
- Функциональный анализ/под общ. ред. С.Г. Крейна. 2-е изд., перераб. и доп. М.: Наука, 1972. 544 с.
- Kan Ch.-H. Ergodic properties of Lamperti operators//Can. J. Math. 1976. Vol. 30, № 6. P. 1206-1214.


