Условия однозначной разрешимости некоторых линейных сингулярных функционально-дифференциальных уравнений

В статье рассматривается вопрос об условиях нетеровости и фредгольмовости линейного функционально-дифференциального уравнения, определенного на конечном отрезке и имеющегося сингулярность в левом и правом концах отрезка.

Описание объекта исследования. Рассмотрим требуемые в работе функциональные пространства. Пусть L pp , 1 <  p <^ - пространство суммируемых с p -й степенью функций z : [ 0; b ] > R с нормой

b

II z L = Л z ( t )| ^p

V 0

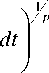
; Dp - пространство абсолютно непрерывных функций x: [0;b]> R , производная которых является элементом пространства Lp, с нормой ||x||Dp = |x||Lp + |x(0)|; D0p - подпространство функций xе Dp таких, что x(0) = 0, с нормой ||x||Dp = |x||Lp.

Основным объектом исследования является сингулярное по независимой переменной функционально-дифференциальное уравнение первого порядка

( Lx ) ( t ) = x ( t ) + h ( t ) x ( t ) + ( Tx )( t ) = f ( t )                    t е [ 0; b ]                   (1)

k

Здесь коэффициент h(t) имеет вид h(t) = — + a(t), суммируемая на отрезке [0; b] функция a: [0; b]> R ограничена в существенном на каждом отрезке [е; b], Е > 0 и удовлетворяет предельному условию lim ta(t) = 0. Функция h(t) не суммируема на отрезке [0; b] и терпит разрыв второго рода в t >0+                                                                                                        L J точке t = 0 .

Оператор T: Dp > Lp вполне непрерывен. В качестве оператора T могут, например, рассматриваться операторы, определяющие сосредоточенное отклонение (Tqx) (t) = q(t)xg (t) или b распределенное отклонение аргумента (Trx)(t) = Jx(s)dsr(t; s). Здесь q е Lp, функция g(t) измерима на отрезке [0; b ], xg (t) =

'x ( g ( t )), g ( t ) е [0; b ]                                                                      _r , _r ,

‘    0    (f) ^[0 b] ; Функция r(t; s) измерима в квадрате [0; b]x[0; b] и b

r ( • ; s ) e L p , var r ( • ; s ) e L ^p , r ( t ; b ) = 0. Эти условия гарантируют [1, с. 56] полную непрерывность S = 0

операторов T_q и T_r соответственно.

Правую часть уравнения (1) будем рассматривать как элемент пространства L ^p . Решение будем искать в пространстве D ₀ ^p , то есть фактически будем рассматривать полуоднородную задачу Коши

( L x ) ( t ) = f ( t )                    x (0) = 0

Уравнения вида (1) возникают, например, при изучении процессов, протекающих в химическом реакторе [2], при изучении некоторых задач теории упругости [3]. Большое количество практических задач, при моделировании которых возникают сингулярные уравнения, приведено в монографиях [4,5].

Уравнения для обыкновенных дифференциальных и функционально-дифференциальных уравнений, обладающие аналогичной сингулярностью, привлекали внимание математиков еще в середине прошлого века [6]. Среди более поздних публикаций отметим работы И.Т. Кигурадзе [7], представителей чешской математической школы [8]. Отметим также монографию Н.В. Азбелева, В.П. Максимова, Л.Ф. Рахматуллиной [1].

Основной результат. Доказано, что такие фундаментальные свойства уравнения (1), как нетеровость и фредгольмовость, определяются единственной характеристикой – величиной числа k . Этот результат переносится на уравнения с сингулярностью, сосредоточенной в правом конце отрезка [ 0; b ] , и на уравнения с сингулярностью, сосредоточенной в точках t = 0 и t = b .

Пусть p' = ^Р . Рассмотрим вспомогательное уравнение Р - 1

( 3 x ) ( t ) = x( t ) + h ( t ) x ( t ) = f ( t )            t e [ 0; b ]                            (2)

Лемма . Справедливы следующие утверждения:

• 1)    оператор 3 имеет правый обратный оператор 3 _r ^-1 : L ^p ^ D ₀ ^p тогда и только тогда, когда к *— .

Р

Оператор 3 имеет обратный оператор 3"¹ : L ^p ^ D ₀ ^Р тогда и только тогда, когда к > — ;

Р

• 2)    уравнение (2) имеет решение при любой правой части f e L ^p тогда и только тогда, когда к * — .

Р

Это решение единственно тогда и только тогда, когда к >  —;;

Р

• 3)    уравнение (2) в пространстве D ₀ ^Р нетерово тогда и только тогда, когда к * —, причем при Р

к < — его индекс равен 1. Уравнение (1) фредгольмово тогда и только тогда, когда к > — .

Р                                                                     Р

Доказательство этих утверждений приведено в статье [9].

Теорема 1. Уравнение (1) в пространстве D0Р нетерово тогда и только тогда, когда к *—, причем Р при к < —его индекс равен 1. Уравнение (1) фредгольмово тогда и только тогда, когда к > —. Р                                                                     Р

Доказательство. Оператор T : D ₀ ^Р ^ L вполне непрерывен по условию теоремы. Осталось сослаться на лемму и теорему С.Г. Крейна (цитируется по [1, с. 13]) о том, что свойство нетеровости оператора 3 устойчиво по отношению к вполне непрерывному возмущению T и при таком возмущении индекс оператора не меняется.

Следствие 1 . Пусть к >  —^ и выполнено хотя бы одно из условий:

Р

• а)    однородное уравнение Lx = 0 имеет только тривиальное решение;

• б)    оператор T вольтерров;

• в)    оператор T определяет сосредоточенное отклонение аргумента ( T_qx ) ( t ) = q ( t ) x g ( t ) и справедливо

  хотя бы одно из неравенств || q ( t)c_g ( t )|| <

  
  

  kp' + 1 A p' 1

  
  

  b

  
  

  M

  
  

  или ^q( ⁽ t ) ^ g ⁽ t )|| l . < kM^;

  
  

  г) оператор T определяет распределенное

  
  

  b

  отклонение аргумента ( T_rx ) ( t ) = j x ( s ) d s r ( t ; s ) и

  
  
  
  

  b

  
  

  справедливо хотя бы одно из неравенств var r ( t ; s )

  
  

  s = 0

  
  

  <

  L^p

  
  

  kp' + 1 A p ' 1                    ч

  или var r ( t ; s )

  M

  
  

  b

  
  

  b

  
  

  s = 0

  
  

  L ”

  
  

  k + 1 <------ .

  Mb

  
  

  Тогда уравнение (1) имеет единственное решение при любой правой части f e L ^p .

  Доказательство .

  • а)    Так как при k > —в силу теоремы 1 оператор L фредгольмов и однородное уравнение имеет

  
  

  ^p

  только тривиальное решение, то неоднородное уравнение однозначно части.

  • б)    Определим оператор K 1 : L^p ^ L ^p равенством K 1 = T Л , где уравнения (2). Ядро оператора Л имеет вид:

  
  

  разрешимо при любой правой

  
  

  Л : L ^p ^ D ₀ ^p - оператор

  
  

  Коши

  
  

  Л ( t ; s ) = <

  
  

  t T ^k

  exp

  s J ^P

  
  
  
  

  ■ j a ( t ) d T > 9 ( t — s ), s * 0

  
  

  s

  0,

  
  

  s = 0

  
  

  .

  
  

| 1, t - s Здесь 9 (t — s ) = <

.

^v ' 10, t <  s

Уравнение ( I + K 1 ) z = f является эквивалентным уравнению (1).

Так как операторы T

и Л

I + K ₁

вольтерровы, то оператор K ₁ также вольтерров, его спектральный радиус равен нулю, оператор обратим и уравнение (1) однозначно разрешимо.

• в)    Первое из неравенств (в) гарантирует справедливость неравенства || K 1|| L _p <  1 и, следовательно, однозначную разрешимость уравнения (1).

Если выполняется второе из неравенств (в), то оператор K 1 действует в пространстве L ограниченных в существенном на отрезке [ 0; b ] функций z : [ 0; b ] ^ R с нормой || z || = vrai sup| z ( t )| и t e [ 0; b ]

норма оператора K 1 в пространстве L меньше 1. Значит, и || K J| <  1.

• г)    Доказательство аналогично случаю в).

Поскольку правые части неравенств в) и г) совпадают, то в дальнейшем будем указывать только неравенства для оператора T , определяющего распределенное отклонение аргумента.

Следствие 2. Пусть

k < — , оператор T определяет распределенное отклонение аргумента Р

b

( T r x ) ( t ) = j x ( s ) d s r ( t ; s ) и

справедливо хотя бы одно из неравенств

b var r ( t ; s ) s = 0

< 1 A p ' 1

< —   — или

_L p I b J M

b varr(t; s)

s = 0

<—— . Тогда уравнение (1) имеет решение в пространстве D_n ^p при любой правой части

_L „ Mb                                                          0

f e L^p .

Доказательство аналогично доказательству следствия 1. При доказательстве используется вид правого обратного оператора 5^— = G : L p ^ D ₀ ^p - оператора Грина задачи ( § x )( t ) = z ( t ), x ( b ) = 0. Оператор G является линейным интегральным оператором, ядро которого определяется равенством

G ⁽ t ^; s ) = ^— [ —

I s

— I

k J exp <

j a ( t ) d T 9(s — t ). s

Обобщение основного результата. Пусть теперь D0Р - подпространство функций xе Dp, для которых x(b) = 0. Коэффициент h(t) имеет вид h(t) = _m + a(t), суммируемая на отрезке [0; b] b -1

функция a: [0; b]^ R ограничена в существенном на каждом отрезке [0; b - е], Е > 0 и удовлетворяет предельному условию lim (b-1)a(t) = 0. Функция h(t) не суммируема на отрезке [0;b] и терпит t ^ b-0

разрыв второго рода в точке t = b .

Теорема 2. Уравнение (1) в пространстве D0p нетерово тогда и только тогда, когда m ^—^ , причем p при m < —его индекс равен 1. Уравнение (1) фредгольмово тогда и только тогда, когда m > —. p                                                                     p

Доказательство. Рассмотрим вспомогательное уравнение (6). Изменим направление параметризации отрезка [ 0; b ] . Положим т = b - 1 . Определим соответственно функции a 1 ( t ), f , ( t ) следующим образом:

a 1 ( т ) = - a ( b - T ) = - a ( t );

f _V(T ) = - f ( b - т ) = - f ( t ).

Пусть

x ( b - T ) = x 1 ( т ).

Тогда

—x ( b - T ) = - x '( b - T ) = - x ’ T ). Уравнение (6) примет вид d T

(m      А

( З 1 x ) ( т ) = x^T ) + l — + a 1 ( T ) I x 1 ( T ) = f , ( T ) V т       )

Дальнейшее доказательство аналогично доказательству теоремы 1 и следует из леммы.

Следствие 1. Пусть m > — и выполнено хотя бы одно из условий: Р

• а)    однородное уравнение Lx = 0 имеет только тривиальное решение;

b

• б)    оператор T определяет распределенное отклонение аргумента ( T_rx ) ( t ) = j x ( s ) d_sr ( t ; s ) и

b

справедливо хотя бы одно из неравенств var r ( t ; s )

s = 0

<

Lp

mp ' + 1 А p' 1

или var r ( t ; s ) M

b

b

s = 0

L”

m + 1

<----

Mb

.

Тогда уравнение (1) имеет единственное решение при любой правой части f е L^p .

Доказательство аналогично доказательству следствия 1 из теоремы 1. Отметим, что ядро обратного оператора З"1 = G в этом случае имеет вид

- m

.     ( b -1 ।

G ( t ; s ) =-l  ----I exp ^

V b - s )

-

■ j a ( t ) d T >9{s - 1 ) s

Следствие 2. Пусть m <— , оператор T определяет распределенное отклонение аргумента Р

b

( T_rx ) ( t ) = j x ( s ) d_sr ( t ; s ) и справедливо хотя бы одно из неравенств 0

b var r ( t ; s )

s = 0

b var r(t; s) s=0

. ( 1 А p' 1

< —  — или

Lp V b I M

< ——. Тогда уравнение (1) имеет решение в пространстве DI при любой правой части

L ™ Mb                                                          0

f е L^p .

Доказательство аналогично доказательству следствия 2 из теоремы 1. Отметим, что ядро правого обратного оператора З^- = Л в этом случае имеет вид

- m

. , . ( b -1 ।

Л ( t ; s ) = 1------I exp ^

V b - s )

-

■ j a( т ) d T >9tt - s ). s

Пусть D0p - подпространство таких функций x е Dp, для которых x(0) = 0 и x(b) = 0. Коэффициент h(t) имеет вид h(t) = k —— + a(t), суммируемая на отрезке [0; b] функция a: [0; b]^ R ограничена в t b-t существенном на каждом отрезке £1; b - £2 ], limta(t) = lim (b-t)a(t) = 0. Функция h(t) не t ^0+ t^b-0V '

£ 1 >  0 , £ 2 >  0 и удовлетворяет предельным условиям суммируема на отрезке [ 0; b ] и терпит разрыв второго

рода в точках t = 0 и t = b .

Теорема 3. Уравнение (1) в пространстве

D0 нетерово тогда и только тогда, когда к Ф —и Р m Ф—-7 . Индекс уравнения (1) равен 1 при к <—, m <—. Уравнение (1) фредгольмово при Р                                      Р       Р

к <--;, m >

Р

—^7 и при к > —^ m <  —^7 . Индекс уравнения (1) равен - 1 при к > -

p

p

p

—, m > p

.

p

Доказательство.  Для доказательства воспользуемся пространством D0p S непрерывных на отрезках

0; b

и

b

2; b

функций у : [ 0; b ] ^ R таких, что у (0) = у ( b ) = 0 и их

производная принадлежит пространству Lp . Такие функции могут иметь не более чем конечный разрыв b „                     .. JbI                                   .и в точке t = —. Норма в пространстве DopS — определяется равенством у = у „ .

2                                            12/                                              D 0 S        L"

Каждое решение уравнения (2) совпадает с решением краевой задачи

= 0, t e [ 0; b ]

в пространстве

Р „I b I

D ₀ p S 1 — 1 . Решение уравнения 5 у = 0 может быть записано в виде суммы x 1 (t ) + x ₂ ( t ).

Здесь функция

равна 0 при

b

I к I                           b x1(t) является решением уравнения (51 x) (t) = x(t) +1 — + a1(t) I x(t) = 0 при t e 0;—

;2

и

t ^е 2; b . Функция

x ₂ ( t ) равна 0 при t e 0;-| j и является решением уравнения

( 5 2 x ) ( t ) = x(t ) +1 — + a ₂ ( t ) I x ( t ) = 0 V b - 1        )

видеть, что оператор 5 нормально

mk при te —;b . Здесь a(t) =--+ a(t), a2(t) = —+ a(t). Нетрудно

2                 ¹ b - 1            ² t

b

разрешим тогда и

являются операторы 5 1 и 5 2 , то есть при к Ф

-

11 ind 5 = 2 при к < --;, m < --7 ; ind 5 = 1 при к <

Р       Р

— и ^p

, ^p

------------1

только тогда, когда нормально разрешимыми 1

m Ф—‘ . Далее, ind 5 = ind 5 1 + ind 5 ₂ , то есть

p m >--7 и при к > -

Р

— m < --‘; ind 5 = 0 при

p

p

/ . ^p

к >--7, m >

Р

Из теоремы 2.3 [1, с. 23] следует, что задача (3) нормально разрешима тогда и только тогда, когда

ɶ

ɶ

нормально разрешим оператор 5 и индекс задачи (3) равен ind 5 - 1. Этот же факт имеет место для оператора 5 .

Утверждение теоремы справедливо в силу полной непрерывности оператора T .

Следствие 1. Пусть к >  —^, m <  —^ и выполнено хотя бы одно из условий: Р       Р

• а)    однородное уравнение Lx = 0 имеет только тривиальное решение;

• б)    оператор T вольтерров;

b

• в)    оператор T определяет распределенное отклонение аргумента ( T r x ) ( t ) = j x ( s ) d s r ( t ; s )

  и

  
  

справедливо хотя бы одно из неравенств

b var r(t; s)

s = 0

I kp' +1I p ' 1 < —-- — pbM

или

b var r(t; s) s=0

L

k + 1

< ------ .

Mb

Тогда уравнение (1) имеет единственное решение при любой правой части.

Доказательство аналогично доказательству следствия 1 из теоремы 1. Отметим, что в этом случае обратный оператор 3 1 вольтерров и его ядро

ограничено

сверху функцией

/ x - k

I t I

Л ( t ; s ) = 1-1 exp ^

I s )

_

j а ( т ) d T >9t t - s ).

s

Следствие 2. Пусть k < — , m > —и выполнено хотя бы одно из условий: Р       Р

• а)    однородное уравнение Lx = 0 имеет только тривиальное решение;

• б)    оператор T определяет распределенное отклонение аргумента

b

( Tx ) ( t ) = j x ( s ) d_sr ( t ; s )

и

справедливо хотя бы одно из неравенств

b var r(t; s) s=0

I mp +1 I p 1 < —- —

L p I b ) M

или

b var r(t; s) s=0

L”

m + 1

<------.

Mb

Тогда уравнение (1) имеет единственное решение при любой правой части f е L p .

Доказательство аналогично доказательству следствия 1 теоремы 1. Отметим, что ядро обратного оператора 3 1 = G в этом случае ограничено сверху функцией G(t; s) =

b - t b - s

- m

t- exp M

а ( т ) d T>6( s -t ).

Следствие 3. Пусть k < — , m < —, оператор T определяет распределенное отклонение p       p

b

аргумента ( T_rx ) ( t ) = j x ( s ) d s r ( t ; s ) и справедливо хотя бы одно из неравенств var r ( t ; s )

s = 0

. 1 1 1 ^p 1

< —  — или

_L p I b ) M

b var r ( t ; s ) s = 0

< —— . Тогда уравнение (1) имеет решение при любой правой части. L ™ Mb

Доказательство аналогично доказательству следствия 2 теоремы 1. Ядро правого обратного оператора 3 _r ^{- 1} = G в этом случае имеет вид

G ( t ; s ) =

-

+

t

s

t

s

- k

- k

b - 1

- m

t

b - s

exp <

-

г                        I b

J a^{( T} ) ^{d T}\^{e (s -} t ) ^ k

J                      12

s

-

t I +

b - t

b - s

- m

exp <

t

.

-

■ ja(T)dT\9(t-s)91 t

-

s

b

Заключение. В работе получены условия нетеровости и фредгольмовости для сингулярных по независимой переменной функционально-дифференциальных уравнений. Также получены эффективные признаки разрешимости и однозначной разрешимости.