Условия осцилляционности функции Грина разрывной краевой задачи для уравнения четвертого порядка

В настоящей работе рассматривается разрывная краевая задача, для обыкновенного дифференциального уравнения четвертого порядка, являющаяся моделью стержневой конструкции. Изучается вопрос об осцилляционности функции Грина. Осцилляцион-ные ядра, примечательны тем, что интегральные операторы с такими ядрами обладают комплексом замечательных спектральных свойств, характерных для классической задачи Штурма. — Лиувилля и называемых осцилляционными.

Всюду в данной работе мы придерживаемся идеологии дифференциальных уравнений на. геометрических графах [1, 2]. На наш взгляд такой подход более удобен, поскольку, во-первых, позволяет опираться на. общие результаты, полученные для уравнений на. графах, а, во-вторых, не смотря на. то, что в данной статье мы рассматриваем задачу о балке с одной упругой опорой, основные результаты без каких-либо затруднений обобщаются на. случай большего числа, опор.

Вопросы, связанные с функцией Грина, разрывных краевых задач уже изучались ранее. Помимо уже упомянутых монографий [1, 2], имеется цикл работ Ю. В. Покорного, А. В. Боровских и К. П. Лазарева, посвященных вопросам о принадлежности функций Грина, разрывных краевых задач к классам осцилляционных и знакорегулярных ядер [3-8]. В частности, в работах [3, 7] была, доказана, осцилляционность функции Грина. краевой задачи, моделирующей малые деформации цепочки шарнирно сочлененных стержней, а. в работе [8] формулируются достаточные условия знакорегулярности функции Грина, разрывных краевых задач, обобщающие известный результат Калафати — Гантмахера. — Крейна. [9].

В центре внимания настоящей работы — задача, которая получила, название «балка. с упругими опорами». Вопрос о положительности и, тем более, осцилляционности функции Грина, этой задачи нетривиален даже в случае одной опоры: если жесткость опоры равна, нулю, то выполнены достаточные условия знакорегулярности (а. значит и

осцилляционности) функции Грина, сформулированные в работе [8]. Если же жесткости опор стремятся к бесконечности, то мы в пределе получаем функцию Грина так называемой «задачи с шарнирной опорой», которая меняет знак «в шахматном порядке» (эта задача и ее обобщения исследовались Н. В. Азбелевым, Ю. В. Покорным, В. Я. Дерром и А. П. Тептиным (см. работы [10-12] и библиографию в них). Поэтому естественным является вопрос — будет ли функция Грина положительна при заданном положительном значении коэффициента жесткости. В работах [13, 14] установлены необходимые и достаточные условия положительности и осцилляционности функции Грина, в которых определяется промежуток значений коэффициента жесткости опоры, при которых функция Грина положительна и вне которого у нее теряется это свойство. Указанный промежуток определяется линейным неравенством относительно коэффициента жесткости [13]. Причем показано, что условия положительности и осцилляционности функции Грина совпадают [14].

В данной статье доказан алгоритмически эффективный критерий положительности, а значит, и осцилляционности, функции Грина. Условия формулируются в терминах свойств однозначно определяемого решения однородного уравнения и идеологически перекликаются с условиями неосцилляции дифференциального уравнения (см. [15, 16] или [2, гл. 3]) и условиями осцилляционности функции Грина «классических» двухточечных краевых задач [17]. Не смотря на то, что, в отличие от результата работы [13], этот критерий не позволяет явно определить «критическое» значение коэффициента жесткости опоры, при переходе через которое теряется свойство положительности (а значит, и осцилляционности) функции Грина, он имеет свои преимущества. Помимо того, что этот критерий допускает эффективную проверку при помощи вычислительной техники, он также позволяет получить некоторые результаты качественного характера. В частности, удается «оценить» границы области положительности функции Грина. Кроме того, этот результат позволяет доказать независимость знаковых, а следовательно, осцилля-ционных, свойств функции Грина от способа закрепления концов стержневой системы.

1.    Постановка задачи

Обозначим через Г интервал (ai,a2) G R с фиксированной внутренней точкой ф G (a1,a₂). Через C [Г] обозначим пространство кусочно-непрерывных функций, допускающих разрыв только первого рода и только в точке ф Тогда для функции u(x) G C [Г], под и(ф ± 0) будем понимать соответствуюнще пределы. Через C ^к[Г] обозначим пространство функций из C [Г]. именмних к производных, также прнпадлежатннх C [Г]. Для интервалов (а1,ф) и (ф а₂) введем отдельные обозначения — Y1 ii Y2 соответствешю.

Пусть u G C [a, b] ii имеет копенное число нулей на [a, Ь]. Через au(x ± 0) обозначим знак u(x) справа, (смева) от тонки х. Использование au(x ± 0) позволяет нам в случаях, когда u(x ± 0) = 0, приписывать этому нулю вполне определенный знак. Если же u(x) = 0, то, очевидно, au(x + 0) = au(x — 0) = sign u(x).

Рассмотрим дифференциальное уравнение

(p(x)u⁰⁰)⁰⁰ — (q(x)u⁰)⁰ = f (x), x G Y1 U Y2,

e коэффициентами p G C ²[Г]. inf _xer p(x) > 0. q G C 1[Г]. q(x) > 0 на Г iif G C [Г]. снабженное в точках a1 11 a₂ краевыми условиями

u(a1 ) + a(a1)D3u(a1) = 0,   P(a1)u⁰(a1) — в (a₁)u⁰⁰(a₁) = 0,

u(a2) - a(a2)D3u(a2) = 0, ^(a2)u0(a2) + в(a2)u00(a2) = 0, а в точке е — условиями согласования u^ - 0)= u^ + 0), u0(£ - 0)= u0(£ + 0), (pu00)^ - 0) = ^")^ + 0),

D3u(е - 0) - D3u(e + 0) - ме) = 7(е), где через D3u обозначена, третья квазипроизводиая (p(x)u00)0 - q(x)u0. а 5, f (е) G R.

В данной работе нам представляется более удобным смотреть на, систему соотношений (1) и (3), (4) как на, реализацию дифференциального уравнения на, геометрическом графе [1], т. е. как на, единый объект

Lu = F ( x ) , x G Г ,                                   (5)

левая часть Lu которого — это левая часть уравнения (1) вместе с равенствами (3) и левой частью условия (4), а, правая часть —

F ( x ) = {

f ( x ) , если x G Г \е ;

f (x), если x = е.

Решением дифференциального уравнения (5) будем называть всякую функцию u(x) G C ⁴[Г], удовлетворяющую на Г\е обыкновенному дифференциальному уравнению (1), а в точке е — условиям (3), (4). Тогда краевая задача (5), (2) — это система (1), (3), (4) вместе с граничными условиями (2).

При исследовании краевой задачи (5), (2) мы будем предполагать, что выполнены следующие условия:

• (а)    p G C²[Г], inf p(x) > 0. q G C¹[Г]. q > 0 на. Г. f G C[Г]: x∈Γ

• (б)    <), вС) > 0, <) + в0=0;

• (в)    5 > 0.

2.    Предварительные сведения и вспомогательные результаты

Задача (5), (2) описывает малые деформации системы, состоящей из двух жестко соединенных стержней с упругой опорой в точке стыковки [18]. Коэффициенты уравнения (1) задают реакцию системы на изгиб и растяжение, коэффициент 5 в условии (5) задает коэффициент жесткости опоры, а, условия (2) охватывают все известные случаи закрепления концов стержней.

Как уже отмечалось выше, нас интересуют условия осцилляционности функции Грина, краевой задачи (5), (2). А поскольку необходимым и достаточным условием осцилляционности функции Грина, рассматриваемой задачи является ее положительность [14], то нам достаточно изучить вопрос о ее положительности.

Функцией Грина невырожденной краевой задачи (5), (2) назовем функцию G(x, s) : Г х Г ^ R такую, что решение задачи может быть представлено в виде

u ( x ) =

G ( x, s ) F ( s ) ds + F ( е ) G ( x, е ) -

Γ

В работе [13] было установлено, что краевая задача, (5), (2) однозначно разрешима, и является самосопряженной. Поэтому функция Грина, задачи существует и обладает свойством симметричности G(x, s) = G(s,x). Кроме того, согласно результатам [1], функция Грина, краевой задачи (5), (2) обладает следующими свойствами:

• 1)    функция G(x, s) вместе со своими производивши по x до четвертого порядка непрерывна по совокупности переменных вплоть до границы на каждом из прямоугольников Yi х Yk (i = k) ^{и на} каждом из треугольников, на которые диагональю x = s разбивается квадрат Yi х Yi (i, k = 1, 2):

• 2)    при каждом фиксированном s Е Г функция G(x, s) по x удовлетворяет однородному уравнению (5) на. x Е Г\s:

• 3)    при каждом фиксированном s Е Г функция G(x, s) по x удовлетворяет всем краевым условиям (2);

• 4)    функция G(x, s) на диагонали x = s удовлетворяет условиям непрерывности вместе dG(x,s) d2G(x,s)

2 x

D³G(s + 0,s) - D3G(s — 0,s) = 1;

• 5)    функция G(x,s) условиями l)-4) определяется однозначно.

Из свойств 1) и 2) следует, что функция G(x,s) непрерывна на замкнутом квадрате Г х Г.

Заданная на, Г краевая задача. (5). (2) может иыть редуцирована. к задаче на. Y1 со специальными краевыми условиями, если правая часть дифференциального уравнения (5) равна нулю на Y2 Такая редукция очень удобна при анализе функции Грина, которую можно считать решением уравнения, правая часть которого сосредоточена, в одной точке.

Для произвольной функции u(x) Е C^к[Г] обозначим через ui(x) ее сужение на интервал Yi и положнм и^(Ф) = u^(j)^ — 0). u2j) (Ф) = u^(j^(Ф + 0). j = 0,1,... , k. Тогда, если f (x) = 0 при всех x Е 72, то исходная задача (5), (2) эквивалентна набору из:

• 1)    неоднородного уравнения на 71 = (a1 , Ф);

• 2)    однородного уравнения на Y2 = (Ф,а₂)

’|ус,оиШ u2(0 = MO- u2(0 = ЩН ЫОЩСЫ £««<»

• 4)    условия согласования третьих квазипроизводных D³U2(ф) = D³ и1(Ф)-5и1(Ф)-f (Ф)-Как уже было отмечено, краевая задача. (5), (2) является невырожденной. Этот факт позволяет получить для сужения u₂(x) следующее представление:

U2 (x) = U1^)z20 (x) + U^(Ф)z21 (x),                              (6)

где z2o(x) — решение одпородпого уравнения (1) на. Y2 = (Ф, a2)• удовлетворяющее граничным условиям z2o(Ф) = 1. z2o(^) = 0 ii условиям (22) в тс)чке a2. а z21(x) — решение однородного уравнения (1) на Y2, удовлетворяющее граничным условиям z21 (Ф) = 0, z21 (Ф) = 1 п условиям (22) в тс)чке a2.

Подставляя полученное выражение (6) в условие из (3) для вторых производных в точке ф получим

ЫФХ (Ф) + в1 U (Ф) + и (Ф) = 0,                       (7)

где в1 = —P2(€)z201 (Ф)- во = — Р2(ФМо(Ф) (напомним. тгто функция p(x) может иметь разрыв в точке Ф).

Рассмотрим теперь условие согласования третьих квазипроизводных в точке ф Используя (4) и (6), получим

D3ui(ф) + %i и1(ф) + %ои1(ф) = .eG^),                             (8)

где %1 = —D3Z21 (Ф) 11 %о = —D³Z20 (Ф) — 5.

Условия (7), (8) вместе с (2Д и дифференциальнь im уравнением (1) на Y1 = (ai, Ф) образуют полноценную, самостоятельную краевую задачу на [a1, ф].

Теорема 1. Краевая задача (5), (2) на Г с F ( x ) равной нулю вне y 1 = [ ai, ф ] эквивалентна. двум задачам:

• 1)    невырожденной самосопряженной краевой задаче па [ a1, ф ]

⁽p^(x)u'⁰⁾⁰0 - ⁽q^(x)u'⁾⁰ = f^(x), x ^{G (}ai, £ ) ,

u ( a1 ) + a(a1 )D3u(a1 ) = 0 , ^(a1)u⁰ (a1) — в(а1 )u00 ( a1 ) = 0 ,                 (9)

p(C)u00(C) + eiu0(€) + eou(O = 0 D3u(C) + %iu(C) + %ои(ф) = /(£), с коэффициентами, удовлетворяющими условиям в1 > 0, во = -%1 > 0, %о < 0 и в1 %о -в0%1 < 0:

• 2)    невырожденной задаче на [ ф, a₂ ] для однородного уравнения

(p(x)U00)00 — (q(x)U0)0 = 0, x G (ф,a2), с неоднородными краевыми условиями

U ( Ф ) = u(0, U 0 ( Ф ) = u’(0,

U ( a2 ) — a ( a2 ) D3 U ( a2 ) = 0 , ^ ( a2 ) U ⁰ ( a2 ) + в b)U00 ( a2 ) = 0

па грапппе промежутка (а₂Д).

Идеи доказательства теоремы те же, что и в работе [19]. На подробностях не останавливаемся.

Из теоремы 1 следует, что на диагональном квадрате yi х Y1 функция Грина G(x,s) задачи (5), (2) совпадает с функцией Грина «классической» двухточечной краевой задачи (9), для которой выполнены условия теоремы Калафати — Гантмахера — Крейна [8, 9]. Следовательно, функция Грина краевой задачи (9) является знакорегулярным, а значит, осцилляционным ядром. Как следствие этого свойства и теоремы 1 получаем, что функция Грина G(x, s) задачи (5), (2) строго положительна на открытых квадратах Yi х Y1¹¹ Y2 х Y2- Отсюда, в свою очередь, следует неотрицательность срезки g^ (•) = G(^, ф) па. веем интервале Г. Покажем, что срезка, g^ (•) = G(o£) строго положительна на Г. Для этого воспользуемся следующим свойством функции Грина:

Лемма 1 [13]. Пусть G(x,s) — функция Грина задачи (5), (2). Тогда для любого s G ( a1, ф ] срезка g_s0 = G ( •, s ) имеет на [ ф, a₂ ) не более одного нуля (с учетом кратности).

Понятно, что в формулировке леммы 1 мы можем поменять местами граничные точки ai 11 a₂. Поэтому из леммы 1. иеотрпцателыюстп срезки g^ (x) ii ее гладкости на. всем интервале Г (свойства, 2 и 4 функции Грина) получаем, что g^ ( x ) >  0 на Г.

С учетом предыдущих рассуждений и симметричности функции Грина, получаем такое утверждение:

Лемма 2. Функция Грина G(x,s) задачи (5), (2) строго положительна на полузамкнутых квадратах ( а1,ф ] х ( ai, ф ] ii [ ф,а₂ ) х [Д а₂).

Отметим, что в работе [13] этот же результат был получен из совершенно иных соображений.

Замечание 1. Из леммы 1 следует импликация: если функция Грина, задачи (5), (2) равна нулю в некоторой точке прямоугольника Y1 х Y2, то в этом же прямоугольнике найдется точка, в которой функция Грина, строго меньше нуля.

Замечание 2. Лемма 1 справедлива для любого нетривиального решения однородного уравнения (о) на Г. удовлетворяющего краевым условиям (22).

ЗАМЕЧАНИЕ 3. В [13] показано, что если u(x) — нетривиальное решение однородного уравнения (5) на. Г. удовлетворяющее условиям (22). то из равешмва u(xo) = 0в некоторой точке xo Е [a_i,a₂) следует не равенство u'(xo + 0)u''(xo + 0) < 0.

3.    Положительность функции Грина краевой задачи (5), (2)

Теорема 1 позволяет установить формулы, по которым можно судить о поведении функции Грина. G(x,s) задачи (о). (2) в тек елз"чаях когда, переменная s Е Г принимает значения близкие к граничным точкам. Для этого определим пару функций w_a1 (x) и y_a1 (x). которые являются решениями однородного уравнения (5) на. Г. удовлетворяющими в тонко a₂ краевым л"словням (22). а в ■точке a_i — условиям

Wai (ai)+ a(ai )D³w(ai) = 1, ^(ai)w^ 1 (ai) - в(a^w^ (ai) = 0, (10i) yai (ai)+ a(ai)D³y(ai) = 0, ^(ai)ya 1 (ai) - в(а1)у^1 (ai) = 1. (Ю2)

Меняя в определении функций w_a1 (x) и y_a1 (x) ролями кош щвые точки a_i и a₂, получим еще одну пару функций w_a2 (x) и y_a2 (x). Поскольку краевая задача (5), (2) невырождена, то функции wai (x) и yai (x) определены однозначно.

Обозначим через lj (•), j = 1, 2, 3,4, функционалы, определяющие краевые условия (9) (в том же порядке, в котором они идут в (9)), а через фj (x) — фундаментальную систему решений уравнения (9) такую, что lj (фк ) = S^j, г де Skj — символ Кронекера. Из свойств 1)-4) функции Грина следует, что при любом фиксированном s Е Yi ФУ^Нкция g_s = G(^,s) является решением однородного уравнения (1) на. Г\(a₁,s). удовлетворяющим условиям (22). Поэтому сутцествутот постоянште ^ и X- зависящие от s Е Yr такие, что при x Е Г\(a₁, s) для функции Грина краевой задачи (5), (2) имеет место представление

G(x,s) = Wai (x)^(s) + yai (x)x(s), (11)

где

₌ _     [ф ;^2,3 , 4]( s )                ₌      [ф ;^1,3 , 4]( s )

П)      p(s)[ф;1, 2,3,4](s), X( )    p(s)[ф;1, 2,3,4](s), а через [ф;ii,... ,ik] обозначен вронскиан системы функций {фij}j=p

Действительно, в треугольнике a_i< s < x < £ функция w_a1 (x)^(s) + y_a1 (x)x(s) совпадает с функцией Грина, двухточечной краевой задачи (9) (см., например, [1, гл. 6]) и, согласно теореме 1, совпадает с функцией Грина G(x, s) задачи (5), (2). Из очевидных включений w_a1 (x),y_a1 (x) Е C[Г] и ^(s),x(s) Е C[ai, £] следует, что рассматриваемая функция непрерывна на множестве {(x,s) Е Г х Г : s Е Yi, x Е Г\(a₁, s)}. Кроме того, при каждом фиксированном s Е Yi Фу^н кция w_a1 (-^(s) + y_a1 (-)x(s) является решением однородного уравнения (5) на промежутке Г\(a₁, s) и удовлетворяет условиям (22). Поэтому из свойств 1)-5) функции Грина, следует, что формула. (И) определяет функцию Грина краевой задачи (5), (2) на множестве {(x,s) Е Г х Г : s Е Yi, x Е Г\(a1, s)}.

Лемма 3 [17]. При s ^ a_i функция x(s) > 0 является бесконечно малой порядка не большего двух, а функция ^ ( s ) удовлетворяет соотношению ^ ( s ) = o ( x ( s ))-

Лемма 4 [1, гл. 6]. Если коэффициент a ( a _i) краевой задачи (9) больше нуля, то при s = ai ерезка G ( x,a_i ) пропорциональна па Г решешно w_a1 ( x ) с положительным коэффициентом пропорциональности, т. е. ^ ( a_i ) >  0 и x ( a_i ) = 0.

Очевидно, что мы можем поменять ролями граничные вершины графа и получить формулу, аналогичную (11), которая будет описывать функцию G(x, s) при s Е Y2 ^и х Е Г\(s, a₂ ).

Поставим в соответствие каждой граничной точке ai функцию, определяемую следу-то щим образом:

, х     \ wa;(х)

^a(ai⁾ = ^0;

a(ai) = 0.

u« W = Ы yai(x),

Теорема 2. Пусть функция uai(x) не равна нулю в точке хо Е Г. Тогда существует такое т = т(хо) > 0, что при 0 < |s — ai | < т (s Е Г) для функции Грина краевой задачи (5), (2) выполнено соотношение sign G(xo,s) = sign Uai(хо).

<1 Согласно (11). при всех s Е Г. достаточно близких к граничной точке ai. имеет место равенство

G(xo,s) = Wai (хо N(s) + yai (хо )x(s).

Если a(ai) = 0. то uai(хо) = wai (хо) = 0 и. ввиду леммы 4. ^(ai) > 0 1i x(ai) = 0. А так как функции ^(s) 11 x(s) пепрерыв! ibi. to при s достаточно близких к ai знак величины G(xо,s) совпадает со зшпсом произведения wai (хо)^(s). т. е. со знаком uai(хо).

Если же a(ai) = 0. то воли: зи тонки ai. ввиду л сипы 3. x(s) > 0 1i ^(s) = o (x(s))- Поэтому при s достаточно близких к граничной точке ai зиак G(xо, s) совпадает со знаком произведения yai (xо)x(s)■ который, в свою онере,ть. совпадает со знаком uai(хо). B

Следствие. Каково бы ни было значение коэффициента 5 >  0 в условии (4), функция u_a1 (х) положительна па полуинтервале (a1Д]. а фуакция u_a1 (х) положительна па полуинтервале [£, a₂).

< Ввиду полной аналогии рассуждений, докажем справедливость утверждения только для ua1 (х). В силу леммы 2. при всех х Е (a1,£] будем иметь aG(x1 a1 + 0) > 0. Из этого неравенства и теоремы 2 следует, что ua1 (х) > 0 для каждого х Е (a1,£]. Следовательно, доказываемое утверждение может быть нарушено, если функция ua1 (х) имеет кратный нуль хо Е Y1 или> если ua1 Д) = 0. В первом случае, ввиду невырожденности краевой задачи для уравнения (5) на (хо, a2) С Г с любыми краевыми условиями вида (2), получается, что ua1 (х) = 0 на (xо,a2). Отсюда и из теоремы единственности сразу следует тождественное равенство ua1 (х) = 0 на всем Г, что, очевидно, неверно. Следовательно, ua1 (х) > 0 нa Y1 и ua1 Д) > 0. Покажем, что в последнем неравенстве знак равенства не возможен. Для этого нам понадобится результат работы [13], согласно которому, для всякого решения однородного уравнения (5) на интервале (хо, a2) С Г, удовлетворяющего условиям (22) и сти(хо + 0) > 0, сти0(хо + 0) > 0, сти00(хо + 0) < 0

выполнено неравенство D3u(xо + 0) > 0.

Предположим, что u_a1 Д) = 0. Тогда, с одной стороны, из определения функции u_a1 (х) и замечания 3 еле дуют неравенства u⁰_a1 (a1 + 0) > 0 и ^1 (a1 + 0) < 0, откуда получаем D³ u_a1 (a1 + 0) > 0. Ас другой стороны, из уже доказанного неравенства ua1 (€ — 0) > 0 ii того же замен;мшя 3 получаем u⁰_a1 Д + 0) < 0 1i Д01 (£ + 0) > 0. откуда

D³u_a1 (£ + 0) < 0. Поскольку функция u_a1 (x) является решением однородного уравнения (5). то D3u_a1 (x) = const iia. Y1- Поэ тому D3u_a1 (a1 + 0) = D3u_a1 Д — 0) > 0 ii

D3Uai (£ — 0) — D3Uai (£ + 0) — 6Uai Ю > 0,

• t. e. функция u_a1 (x) не может быть решением однородного уравнения (5). Полученное противоречие доказывает, что u_a1 Д) > 0, а значит, u_a1 (x) > 0 на (а1Д]. B

Теорема 3. Функция Грина краевой задачи (5), (2) строго положительна на Г х Г тогда и только тогда, когда хотя бы одна из функций u_a1 (x) или u_a2 (x) положительна па всем интервале Г.

C Необходимость. Поскольку функция Грина положительна, то из теоремы 2 вытекает, что обе функции uai (x) неотрицательны на Г. А из следствия теоремы 2 и леммы 1 следует, что обе эти функции не могут иметь кратных нулей на Г. Следовательно, uai (x) > 0 на. Г.

Достаточность. Для определенности, будем считать, что ua₂(x) > 0 на Г. Предположим, что теорема не верна. Тогда из замечания 1 следует существование точки (xo, so) Е Y2 х Y1 такой, что G(xo, so) < 0. Из непрерывности функции Грина на прямоугольнике Y2 х Y1 и пера.веиств aG(a₂ — 0, s) > 0 щ: >ii s Е 71 (теорема 2). G(£, s) > 0 при s Е Y1 11 g^ (x) = G(x,€) > 0 щin x Е Y2 (лемма 2) следует сутцествоваппе точки (x*,s*) прямоугольника. Y2 х Y1 тако!i. что G(x*,s*) = dG(x*, s*) = 0 (например, можно взять s* = inf {s Е (s₀,£) C Yi ^: gs(x) > 0 ii a Y2} 11 x* — такуао. что gs*(x*) = 0). Но. согласно утверждению леммы 1, срезки gs (x) функции Грина не имеют кратных нулей на Y2 при s Е Y1- Полученное противоречие окоинате.тыю доказывает теорему, в

Поскольку необходимым и достаточным условием осцилляционности функции Грина, краевой задачи (5), (2) является ее положительность [14], то имеет место утверждение:

Следствие 1. Функция Грина краевой задачи (5), (2) является осцилляционным ядром тогда и только тогда, когда хотя бы одна из функций u_ai (x) или ua₂ (x) положительна па всем интервале Г.

Следствие 2. Функции u_ai (x) и ua₂ (x) либо обе положительны на всем множестве Г, либо имеют ровно по одному простому нулю на Г. Во-втором случае, нуль функции u_ai (x) лежит впут}ш интервала Y2 а нулв <1>упкппп ua₂ (x) лежит впут}ш интервала Y1.

C Действительно, если, шгпрпме]). предположить, что функция ua₂ (x) положительна на Г, а функция u_ai (x) нет, то, в силу замечания 2 и следствия теоремы 2, функция u_a1 (x) принимает отрицательньie значения на интервале Y2- Тогда, с одной стороны, из теоремы 2 следует, что функция Грина, краевой задачи (5), (2) принимает отрицательные значения, а, с другой стороны, из теоремы 3 следует, что она. положительна, на. всем квадрате Г х Г. Полученное противо}течне доказывает, что u_a1 (x) > 0 на Г. B

Следствие 3. Функция Грина краевой задачи (5), (2) является осцилляционным ядром тогда и только тогда, когда выполнено хотя бы одно из неравенств au_a1 (a₂ — 0) > 0 или aua₂ (a1 + 0) > 0.

C С учетом следствий 1 и 2. достак>нио показать, что из неравенства au_a1 (a₂ — 0) > 0 следует u_ai (x) > 0 нa Y2- Поскольку u_a1 (Д > 0 (следствие теоремы 2) и функция u_a1 (x) имеет на интервале Y2 не более одного простого нуля (следствие 2 теоремы 3), то u_a1 (x) > 0 при всех x Е Y2- ^а значит и при всех x Е Г. Для фуикции u_a1 (x) рассуждения аналогичные, в

Лемма 5. Пусть функция u_a1 (x) равна нулю в точке x* Е Y2- Тогда при s Е (x*, a₂) C Y2 ерезка g_s(x) меняет зшж па ребре Y1- а при s Е (^, x*] C Y2 <-резка. g_s(x) положительна па Г.

<1 Ввиду следств! 1Я 2 теоремы 3. u_a1 (x) < 0 на (x*,a₂) 1i u_a1 (x) > 0 на. (£,x*). Если x* < s < a₂. то. ввиду теоремы 2. ag_s(a1 + 0) < 0. а ввиду леммы 2. gs(£) > 0. Следовательно. функция gs(x) меняет знак па. ребре Y1-

Если же £ < s < x*. то. ввиду теоремы 2. ag_s(a1 + 0) > 0. а ввиду .теммы 2. g_s(£) > 0. Поскольку функция g_s(x) имеет на Y1 = (ai ,£) ^не более одного простого нуля (лемма 1), то g_s (x) > 0 iia Y1 и. вследствие леммы 2. полупаем g_s(x) > 0 на Г.

Нам остается показать, что срезка gx* (x) положительна на Г. Здесь мы воспользуемся непрерывностью функции Грина и тем, что g_s(x) > 0 на Г при всех s Е (£,x*) С Y2- При s ж x* — 0 будет выполнять>ея соотношение g_s(x) ж gx* (x) > 0. А поскольку срезка. gx* (x) не имеет кратных нулей на Г. т о gx* (x) > 0 на Г. B

Доказанная лемма позволяет выделить на Г х Г подмножество на котором знакопеременная функция Грина, заведомо будет положительна.

Теорема 4. Пусть функция u_a1 (x) равна нулю в точке x2 Е Y2, ^а ФУнкция u_a2 (x) равна пулю в точке x1 Е Y1- Тогда функция Грппа краевой задачи (5). (2) строго положительна на множестве, получаемом удалением из квадрата Г х Г двух открытых прямоугольников (a1,x1) х (x₂, a₂) С Y1 х Y2 и (x₂, a₂) х (a1,x1) С Y2 х Y1-

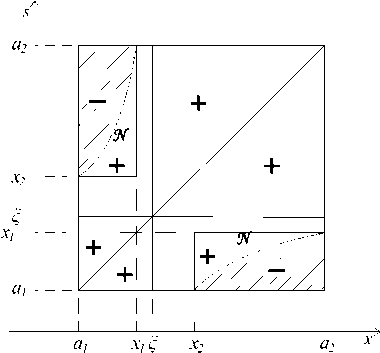
Рис. 1.

Обозначим через N множество всех точек множества Г х Г в которых функция Грина G(x,s) краевой задачи (5), (2) равна нулю. Нас интересует случай, когда N = 0. Из теоремы 4 следует, что все точки N лежат в прямоугольниках (a1, x1) х (x₂, a₂) С Y1 х Y2 и (x₂,a₂) х (a1,x1) С Y2 х Y1, причем всякая прямая, параллельная какой-нибудь из координатных осей, имеет с множеством N не более одной общей точки (леммы 1 и 2). Более того, из этих же лемм и непрерывности функции Грина следует, что множество N не имеет изолированных точек и в любой окрестности точки (x, s) Е N П (Г х Г) функция Грина меняет знак. А поскольку функция G(x, s) симметрична (см. [13]) и строго положительна на диагонали квадрата Г х Г (лемма 2), то можно заключить, что множество N представляет собой пару непрерывных кривых, симметричных относительно диагонали x = s. с концами на сторонах квадрата, Г х Г. При 5 ж то кривые, задающие множество N начинают стремиться к сторонам x = £ и s = £ прямоугольников Y2 х Y1 и Y1 х Y2, а в предельном случае 5 = то совпадает с этими сторонами.

4.    О положительности функции Грина в случае неподвижных концов

Всюду в этом пункте считаем, что в краевых условиях (2) а(а1) = а(а₂) = 0. В данном случае uai (x) = yai (x). Мы обсудим вопрос о тоск как ведут себя функции ya. (x). если мы меняем в краевых условиях (2) значения коэффициентов Р(^), в(•)• Будет показано, что знаковые свойства функций yai(x) не зависят от значений Р(^), в(^-)- Ввиду полной аналогии, мы покажем, что от значений Р(^), в(•) не зависит знак только одной из этих функций, например, y_a1 (x).

Рассмотрим краевую задачу

Lu = 0, x G Г, u(ai) = 0, P(a₁)u⁰(a₁) — в (a₁)u'⁰(a₁ ) = 1,                         (12)

u(a2) = 0, u0(a2)u00(a2) 6 0, и обозначим через Y множество всех ее решений.

Поставим в соответствие каждому единичному вектору (У, в) G R+ с неотрицательными координатами такую функцию u(x) G Y, что векторы (u⁰(a₂),u⁰⁰(a₂)) G R² и (У, в ) ортогональны. Из невырожденности краевой задачи (5), (2) следует, что такая функция существует и единственна. Полученное отображение (У, в) ^ u(x) множества O+ = {(У,в) : У² + в² = 1, в, У > 0} в Y сюрьективно, но, вообще говоря, не является взаимно однозначным. Однако, ввиду непрерывной зависимости решений краевой задачи (5), (2) от коэффициентов краевых условий, это отображение является непрерывным (мы полагаем, что норма, в O+ иидуцировала, из R². а iioj эма в Y — из C3[Г]).

Лемма 6. Пусть функция u(x) G Y удовлетвориет условиям u⁰(a₂) = u⁰⁰(a₂) = 0. Тогда Y = {u(x)}.

C Так как u0(a2) = u00(a2) = 0. то для люб ой функции v(x)  G Y векторы

(u⁰(a₂),u⁰⁰(a₂)) и (v⁰(a₂),v⁰⁰(a₂)) ортогональны некоторому ненулевому вектору (У, в) G O⁺ а. значит удовлетворяют одним и тем же краевым условиям. Из невырожденности краевой задачи (5), (2) следует v(x) = u(x) на Г. B

Следствие. Отображение O + н- Y либо постоянно, либо является гомеоморфизмом.

Лемма 7. Пусть u(x) G Y- Е<-дп au(a₂ — 0) > 0. то для люб ой функции v(x) G Y также будет выполнено неравенство av(a₂ — 0) > 0.

C Из замечания 2 следует. что любая функция v(x) G Y имеет иа. ребре Y2 копенное число нулей. Поэтому величина av(a2 — 0) определен а для всех v(x) G Y-

Предположим, что доказываемое утверждение не верно, т. е. существует функция z(x) G Y для к<порой az(a₂ — 0) < 0. Тогда, в силу леммы 6. вектор (z⁰(a₂),z⁰⁰(a₂)) не нулевой и, ввиду z(a₂) = 0 и (12), принадлежит замыканию второй четверти плоскости, а вектор (u⁰(a₂), u⁰⁰(a₂)). в силу условий u(a₂) = 0. au(a₂ — 0) > 0 и (12). принадлежит замыканию четвертой четверти R². Рассмотрим отображение O⁺ н- Y. Поскольку функции u(x) и z(x) различны, то из следствия леммы 6 вытекает, что это отображение взаимно однозначное и для любой функции v(x) G Y век тор (v⁰(a₂ ),v⁰⁰(a₂)) не нулевой. Пусть (Р_и,в_и) ¹¹ (Pz, в_z) прообразе>1 функций u(x) 11 z(x) при отображешш O⁺ н- Y. При непрерывном стремлении точки (У, в) G O+ от (p_z, в_z) G O+ к (Р_и,в_и) G O+ ненулевой вектор (v⁰(a₂),v⁰⁰(a₂)). соответствующий образу тонки (У, в)- непрерывно должен стремится от (z⁰(a₂),z⁰⁰(a₂)) к (u⁰(a₂),u⁰⁰(a₂)). что не возможно. так как v⁰(a₂)v⁰⁰(a₂) 6 0 и |v⁰(a₂)| + |v⁰⁰(a₂)| > 0 для любо!i функции v(x) G Y- а ветсторы (z ⁰ (a₂),z⁰⁰(a₂)) к

(u⁰(a2),u⁰⁰(a₂)) принадлежат разным четвертям плоскости. Следовательно, какова бы пи была, функция v 6 Y- векторы (v⁰ (a₂),v"(a₂)) и (u'(a₂),u⁰⁰(a₂)) должны лежать в одной четверти плоскости, т. е. av(a₂ — 0) > 0 для всех v 6 Y- B

Рассмотрим теперь вопрос о зависимости знаковых свойств решений задачи (12) от коэффициентов P(a1) и e(ai )• Заменим в краевой задаче (12) краевое условие P(ai)u0(ai) — в(а1 )u"(ai) = 1 па. более общее u00(a1 )u0(a1) < 0, а все остальные условия оставим без изменения. Обозначим через Y* множество всех решений, получившейся краевой задачи. Из замечания 3 следует включение Y С Y*, которое вместе с невырожденностью краевой задачи (5), (2) позволяет сформулировать такое утверждение:

Лемма 8. Y* = {AY, А > 0}.

Действптелыю. если u(x) произвольный э.темент множества. Y. то. каково бы iiii было число А > 0. фуикипя Au(x). в силу замечаишi 3. принадлежит Y*. II наоборот, если u(x) произвольный э.темент множества. Y*. т о ^(a₁)u^,(a₁ ) — в(a1 )u⁰⁰ (ai) = А > 0. Поэтому ¹ u(x) 6 Y.

Теорема 5. Элементы множества Y* либо все строго положительны на Г, либо все знакопеременные.

C С учетом леммы 8. достаточно до казать утверждепие теоремы для Y. Более того, достаточно показать, что из положительности одного элемента из Y следует положительность всех элементов множества Y.

Из определения множества Y следует, что любая функция v(x) 6 Y является решением некоторой краевой задачи для однородного уравнения (5) с краевыми условиями (102). (22). Причем ко'эффшщепты ^(a₂). в(a₂) условия в гранинной точке a₂ определяются координатами вектора (Д в) 6 O+, которому отвечает функция v(x) (если таких векторов более одного, то координатами любого из них). Тогда, в силу следствия теоремы 3. любая функция v(x) 6 Y строго пологкнтельна на. (ai,^] и имеет на интервале Y2 = (£>^а2) ^не более одного простого нуля.

Пусть u(x) — произвольный фнкенроваппый элемент множества. Y 11 u(x) > 0 на Г. Тогда из леммы 7 следует, что для любой функции v 6 Y будет выполнено неравенство av(a₂ — 0) > 0. А поскольку v(x) > 0 ii а x 6 (ai, ^] и фу1нения v(x) имеет на интервале Y2 не более одного проетого нуля, то v(x) > 0 на Г. B

Из теорем 3 и 5 следует, что в случае неподвижных концов, знак функции Грина, задачи (5), (2), а значит, и ее осцилляционность [14], не зависят от коэффициентов ^(^), в(Д Другими словами, знак функции влияния балки с упругой опорой зависит от коэффициента. жесткости опоры, но не не зависит от способа, фиксации ее концов.

Стоит отметить, что если хотя бы один из концов балки является подвижным (соответствующий коэффициент а(-) больше нуля), то коэффициенты $(■) и в(•) уже будут влиять на. знаковые свойства, функции Грина. Этот факт подтверждает следующий пример.

ПРИМЕР. Пусть Г — это интервал (0, 2) С R с фнкенроваиной точкой £ = 1. На Г рассмотрим дифференциальное уравнение (5), определяемое дифференциальным выражением L u = u^IV. x 6 (0,1) U (1,2). ii соотношениями (3). (4). в которых б = 20.

Рассмотрим краевую задачу:

Lu = F (x),  x Е Г,

u(0) + 2D3u(0) = 0, u(i (0) = 0, u(2) = u0(2) = 0, в которой i = 1 ил и i = 2. Согласно теореме 3 и ее следствиям, функция Грина задачи (13) является осцилляционной тогда и только тогда, когда решение uo(x) краевой задачи

Lu = 0, x Е Г,

u(0) + 2D3 u(0) = 1, u(i) (0) = 0, u(2) = u0 (2) = 0

удовлетворяет неравенству auo(2 — 0) > 0. Вычисления показывают, что uo(x)= C1(Ц^ + C2(2—x^, 1 6 X 6 2; 6             2

где C1 « 0.13. C₂ « 0.1 щ hi i = 1 i1 C1 « 0.41. C₂ « —0.06 щ >ii i = 2.

Поскольку u0(2) = C₂. то при i = 1 выполняется неравенство auo(2 — 0) > 0. а при i = 2 — неравенство auo (2 — 0) < 0. Следовавельно, при i = 1 функция Грина краевой задачи (13) является положительной (и осцилляционной), а при i = 2 — нет.