Условия разрешимости задачи Неймана N2 для полигармонического уравнения в шаре

Введение. Пусть S = { x g R n :| x | < 1} - единичный шар в R n , n >  2 , а dS = { x g R n :| x | = 1} -единичная сфера, где | x ¹ = 7 x² + x ² +•••+ x n . В работе [1] были найдены необходимые условия разрешимости следующего класса краевых задач типа Неймана Л4, зависящего от параметра k g N₀ для полигармонического уравнения

Amu = f (x),  x g S;(1)

d k u I _ , , d ^{k + 1}u I _ _z ,     d ^k + ^{m - 1}u I

?i IdS = Ф( x )’^йТ|5S = Ф2(xS = Фт (xX x GdS, ov          ovov где —— внешняя нормальная производная к единичной сфере, т g N. Класс задач Мя является dv частным случаем краевых задач для полигармонического уравнения с нормальными производными высокого порядка в граничных условиях, рассмотренных в [2]. Задача ЛТя является задачей Дирихле, которая, безусловно разрешима, а задача Л/^ совпадает с задачей Неймана [3, 4]. В работе [5] А.В. Бицадзе выписал необходимые и достаточные условия разрешимости задачи N\ при т = 1,2 и показал, что она решается в квадратурах.

Исследования разрешимости некоторых постановок задач типа Неймана в единичном шаре, кроме перечисленных выше работ, можно найти также для бигармонического уравнения (в частности задачи Л/^ и Л/*2) в работах [6-11], а для полигармонического уравнения в работах [12,

Математика

13]. В работе [14] для краевых задач для полигармонического уравнения с нормальными производными в граничных условиях получено достаточное условие фредгольмовости этих задач и приведена формула их индекса. В [15] исследовались полиномиальные решения задачи Дирихле для полигармонического уравнения при полиномиальных данных и приведены формулы, позволяющие легко строить полиномиальные решения задачи.

Задача А/'2. Исследуем частный случай задачи (1)-(2) - задачу Мд для однородного поли- гармонического уравнения, которую можно переписать в виде

A ^mu = 0, x е S ;   Л ^[2] и ^= ф (x ),..., Л ^{[ т + 1]} и | q s = Ф т ( x ), x ed S ,

n где Λ=∑ i=1

∂ xi — , t[m] = t(t-1) ...— -m +1) - m -я факториальная степень t, причем t[0] = 1, и ∂xi

∂iu справедливо равенство Л[i]и = —г на dS. Рассмотрим m -гармоническую в S функцию

∂νi v = Л[2]и . Относительно этой функции получим следующую задачу:

Amv = 0,  x е S, vIds=ф1(x),(A-2)v^ = фд(x),...,(Л-2)[m-1]v^ = фт(x) x eQS, приводящуюся к задаче Дирихле, которая безусловно разрешима, и решение которой будем считать известным и таким, что v е Cm-1(S) .

Рассмотрим уравнение v = Л ^[2] и относительно функции и(x ) в m -гармонических в S функциях. Докажем, что это уравнение разрешимо тогда и только тогда, когда m -гармоническая в S функция v ( x ) в своем разложении в окрестности нуля не имеет членов нулевого и первого порядка малости, а значит задача Мр разрешима. Действительно, если уравнение v = Л ^[2] и разре-

∞ шимо, то раскладывая функции и(x) и v(x) в ряд Тейлора в окрестности нуля и(x) = V ui (x) и i=0

∞

v ( x ) = V и ( x ), учитывая единственность этого разложения и возможность почленного диффе- i = 0

ренцирования ряда для однородных многочленов и (x) и vi (x) степени i получаем равенство vi (x) = Л[2]ui (x) . Значит, так как Л[2] ui (x) = 0 при i = 0,1, то получаем необходимость условий v0(x) = v1(x) = 0. Достаточность этих условий следует из формулы z .       С1 z, . dt . Г1 z, ddt , х .     , х и (x) = -J о v (tx) J + J о v (tx)   + c> (x) + c (x), где ci (x) - произвольные однородные полиномы степени i. Правая часть этой формулы корректна, поскольку v(x) = O(| x |2), | x |^ 0, а значит, несобственные интегралы сходятся. Проверим, что Л[2]и = v. Действительно, так как n∂           n

Лv(tx) = V xi —v(tx) = t V xivx (tx) = tDtv(tx), i=1    dxi             i=1      i и Л[2]ci (x) = 0 , то будем иметь

Л ^[2] и = - ( Л - 1) J_o D_t v ( tx ) dt + Л |_о ( - D_tv (tx ) - -^- v (tx ) ) dt =

= -(Л -1)( v(x) - v(0)) + л(1 v(tx)1 +1" V ^- v(tx) - -1 v (tx)) dt) = t             J0 t2           t

= - ( Л - 1) v ( x ) + Л v ( x ) = v ( x ).

Поэтому при условиях v ₀( x ) = v 1 ( x ) = 0 m -гармоническая в S функция и ( x ) существует и для нее выполнены граничные условия (3). Что и требовалось доказать.

Вспомогательные утверждения. В работе [16] доказано следующее утверждение.

Карачик В.В.

Теорема 1. Для любой m -гармонической в S функции v е C m 1 ( S ) верно равенство

v(0) = — f (^m-» + h(m-'IЛ+^+л[--'Iyds,, ton dS m—1

где числа him-11 - коэффициенты многочлена Hm—1 (2) = ^him 12 (считаем H0 = 1), такого что i=0

(-1) “-1.

H[m-1|(2) = T^^(2 — 2)...(2 — 2m + 2).  .(4)

m

Следует заметить, что если рассмотреть дискретную производную многочлена P ( 2 ) в виде

P(1) (2) = P(2 +1) — P(2), то из (4) будем иметь him-1) = !(H[m-1])(i)(0) .(5)

i !

Из теоремы 1 вытекает, что для функции w(x ) = Л и ( x ), при m -гармонической в S функции и ( x ), верна формула

1   /-1 A m ^-1 . ^m

w(0) =---—-----f У p(m) Л[i] и ds , ton (2m-2)!!JdSisPl          x’ где числа p*k) находятся из равенств

(i 2 k i 1

p i ^k ) = ( - 1) ^{k -} i I

V i-1  )

(2 k - 2i + 1)!!

2 k - 2i + 1

•

Эти числа составляют целочисленный треугольник Неймана Р [1]

-1 P=

- 3

Преобразуем равенство v(0) = Л[2]и(0) к аналогичному виду. Для факториальных полиномов kk

P [k ] ( 2 ) = ^ p i ^k ) 2 ^[ i ¹, соответствующих P_k ( 2 ) = ^ p ^{( k} ) 2 i , верно представление [17] i = 1                                                                i = 1

k

P_v k ] ( 2 ) = £ p i ^k ) 2 ^[ i ^] = ( 2 , - 2) k = 2 ( 2 - 2)( 2 - 2 k + 2), i = 1

где ( a , b ) l = a ( a + b )• • •( a + ( l - 1) b ) - обобщенный символом Похгаммера.

Лемма 1. При k , s ей справедливо следующее равенство

2 ^{[ k ]} 2 ^[ s ¹ = ]Г f s Ъ ^{k +} i ^] k ^[ s ^{- i ]}. i = 0 V i )

Доказательство. Проведем индукцию по s . При s = 1 лемма верна 2 ^{[ k ]} 2 ^[1] = 2 ^{[ k ]} ( 2 - k + k ) = k 2 ^{[ k ]} + 2 ^{[ k + 1]}.

Пусть лемма верна при некотором целом s > 1. Тогда ss

2 ^{[ k ]} 2 ^{[ s + 1]} = ( 2 - s ) ^     2 ^{[ k +} i ^] k ^{[ s -} i ^] =

+

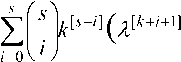
i = 0 V i )

+(k + i - s

s + 1

SL-1)

_k ^[ s ^{- i + 1]} 2 ^{[ k + i ]} + £ I ^s k ^[ s ^{- i + 1]} 2 ^{[ k + i]} =

i = 0 V )

^{s +1} v

=z(Is

^S \ i - ¹

V^)

^[ k + i ^] k ^[ s ^{+ 1 -} i ^]

Шаг индукции доказан, а значит, лемма верна.

Математика

Замечание 2. Если в формуле из леммы 1 заменить индекс суммирования i ^ s — i , то будем иметь

s

2 ^[ k Я ^{s ]} =у| Я k ^{+ s} - i ^] k ^[ i ^].

I i=0 к i 7

Первое условие разрешимости задачи Ы^ . В силу леммы 1 при s = 2 имеем Я ^{k ]} Я ^[2] = к ^[2] Я ^{[ k ]} + 2 k z ^{k + 1]} + Я ^{k + 2]} и, значит, по теореме 1 можно записать 1       m — 1                            1       m — 1

v (0) = — J x £ h i m -°^{A [ i ]} v ( x ) ds x = — J £ h i m - 1) Л ^[ i ^] Л ^[2] u ( x ) ds . = to " Si = 0                       to ' Si = 0

m — 1

= ±J £h

i       m+1            mm

= -LJ(£ him-1 ’ + 2£(i — 1)+ £ i(i — 1)him-"^u(x)dsx. ®n      i=2            i=2

Если добавить нулевые члены hmm—1) во вторую сумму и нулевые члены hmm—1) и h(mm-1) в третью, то будем иметь i v (0) = — J^E (him"1) + 2( i — 1) P-1) + i (i — 1) him—1))л[ i ]u (x) dsx.

Используя формулу (5) найдем h^ + 2( i — 1) him-1 + i (i — 1) h< m—1) = -!-(H[ m-„(2) + (I—2)!

+²⁽H[ m—J^) + ⁽H[ m-^РС») = -2— X

(i — 2)!

x( H[ m —nd) + (H[ m—1])⁽¹⁾(Я) + (H[ m -^P + 1))⁽i^—2)(0) = -2- X ⁽i^{— 2)!}

x( H[ m—1](Я + 1) + (H[ _m—Jp! + 1))⁽i^—2) (0) = -2—(H[ m ^(2 + 2))⁽i^—2)(0). (i — 2)!

Отсюда находим i      m+1

V(0) = —J,_$E

ОS ^шп    i=2

(i — 2)!

(H[ m—1](2 + 2))⁽i^—2)(0) Л^[i^]u (x) dsx =

i      m—1 i

= — J"_9S£ ч( H[ m—1](2 + 2))⁽i РЛ^{4 2]}u (x ) dsx.

®n "^SSi=0 i^!

(—1) m^—1

Из ⁽⁴⁾ с учетом ⁽⁷⁾ Получаем ^H[m—1](2^{+ 2)}= —---— P[m—1]^(Я) , ^а Значит

(2 m — 2)!!

1    / n^m—1   . ^m—1 1              _

v⁽⁰⁾=;; ?& Jds £ i!^{0 Л}i^+2]u<^x > ^dsx=

1       _n m^—1   _ m—1                              i / i\m^—1   _ m—1

=———  Ур(m—1)л[1+2]u(x)dsx = -2-12--- Vp(m—1^ (x)dsx, ton (2m — 2)!!JdS£P1          v' x  an (2m — 2)!!JdS£Pl    P1+1V 7 x где было учтено, что p0m-1) = 0 , а коэффициенты p(m-1) находятся из (6). Значит, первое доста точное условие v(0) = 0 разрешимости задачи Л/*2 приводится к виду

К/Р( m^—1)^2( x) +  + Pmm—^V)^m (x)) dsx = 0.                           (8)

Второе условие разрешимости задачи Л/*₂. Выясним, что означает условие v1(x) = 0 в терминах граничных функций задачи (3). Воспользуемся теоремой 6 из [18].

Теорема 2. Пусть w(x) - гармоническая в S и непрерывная в S функция, тогда имеет место равенство

Используя эту теорему, в примере 4 из [18], была доказана следующая формула

1 г                         1

- L 6^w(^>^ds§ = -wx⁽⁰⁾.

ton ^Г¹             n ⁱ

Пусть w₁ (x) - однородный полином первой степени в разложении w(x) в окрестности нуля, тогда в силу формулы выше для гармонической в S и непрерывной в S функции w(x) верно утверждение

W1( x) = о ^ VH1( x) £Я,® w(£) ds5 = 0, где H1(x) - произвольный однородный гармонический полином первой степени. Заметим, что для m -гармонической (m > 1) в S функции v(x) это не так, например, для функции v(x) = xi (1-| x |2) . Это так, поскольку под интегралом суммируются однородные составляющие 1го порядка всех гармонических компонент из разложения Альманси функции v(x).

Продолжением полученного утверждения на m -гармонические функции является следующая лемма.

Лемма 2. Пусть m -гармоническая в S функция v e Cm^-1(S) , тогда

V1( x) = 0 ^ VH1( x) £H^XA-3)...(Л-2 m +1) v (£) ds. = 0, где H (x) - однородный гармонический полином степени 1.

Доказательство. В силу следующего свойства (Л + 2m)Amu = A^mЛи оператора Л функция v( x) = (Л - 3).. .(Л - 2 m +1) v (x)

является m -гармонической в S и непрерывной в S и пусть ее разложение Альманси в S имеет вид

v(x) = v(0) (x)+1 x |2 v(1) (x) +...+1 x |2m-2 v(m-1) (x), где v(i)(x) - гармонические в S функции. Это возможно в силу звездности области S.

Рассмотрим гармоническую в S функцию w(x) = v⁽⁰⁾ (x) + v⁽¹⁾ (x) +... + v^(m-1) (x).

Докажем, что v(x) обладает свойствами v1 (x) = (-1)m-1 (2 m - 2)!! v (x X  W(x) = v1(xX где w1(x) и v1(x) - однородные полиномы 1-го порядка в разложении w(x) и v(x) в окрестности нуля. Если это так, то v1 (x) = 0 ^ v)1 (x) = 0 ^ w1 (x) = 0 ^ VH1 (x) J^ H1 (^) w(^) ds^ = 0

и поскольку

J5sH1(^) w(^) ds§ = J55H1(^) v(^) ds^, то утверждение леммы будет доказано.

Нетрудно видеть, что поскольку Л | x |²i v⁽i) (x) =| x |²i (Л + 2i)v⁽i) (x), то можно записать

У1 lx |²i v⁽i) (x) = v(x) = (Л - 3)(Л - 2m +1)У x |²i v⁽i) (x) = i=0                                                           i=0

= yix |²ⁱ (Л - 3 + 2i)... (Л - 2m +1 + 2i)v⁽ⁱ) (x)

i=0

Математика

и, значит, в силу единственности разложения функции в формулу Альманси имеем v⁽i) (x) = (Л- 3 + 2i)... (Л- 2m +1 + 2i)v⁽i) (x) .

Поскольку v (x) = v*0) (x) и v1 (x) = v((0) (x), то отсюда следует v (x) = v(0) (x) = (Л - 3)(Л - 2 m +1) v(0) (x) = (-2)... (-2 m + 2) v1 (x)

и значит v1(x) = 0 « v>1(x) = 0. Кроме того, из этой формулы будем также иметь m-1                    m-1                  m-1

wi⁽x) = X vii)⁽x) = v⁾1^{(0) (}x) ⁺ X vi i)⁽x) = ^v1⁽x) ⁺ X ^{(2i - 2)} • • •^{(2i - 2}m^{+ 2)}v⁽i)⁽x) = ^v1⁽x) i=0                            i=1                          i=1

и значит v (x) = 0 « w1 (x) ^ 0. Лемма доказана.

Преобразуем условие ортогональности из леммы 2. Пусть H1(x) - однородный гармонический полином первой степени. С помощью (7), учитывая что v = Л[2]и , запишем m f^H1(^)(Л-3)...(Л-2 m +1) v (^) ds5 = JssH1(^)П (Л-2 j + 1)'Л и (^) ds§ = j=1

mm

= LЛ1(^>L p (m )(Л- 1)[j] Л и (5) ds^ = fsH1(^)£ p (m) Л[ j+1] и (5) ds^ = j=1                                                j=1

m

= fdSH '(5*1 pjm 'pj (5* dsi j=1

и значит второе достаточное условие разрешимости задачи    примет вид

£_$H1(5)(p(^m W5) + ... + pmmⁿ)Pm (5)) ds5 = 0.                        (9)

Итак, достаточные условия разрешимости задачи Ы^ при условии v g Cm^-1(S) имеют вид (8)–(9). Заметим, что условия (8)–(9), согласно результатам работы [1], являются и необходимыми условиями разрешимости задачи Л/^. Например, для 3-гармонического уравнения (m = 3 ) условия (8)–(9) с помощью строк треугольника Неймана записываются в виде

^(-^2(5) + Рз(5))ds§ = 0, J_g$H1(5)(3Р1(5)-3p₂(5) + Рз(5))ds§ = 0.