Условия существования и единственности решений линейных функциональных уравнений в классах первообразных от лебеговских функций на простой гладкой кривой

Начиная с уравнения

J ln |т -t\ф(т ) dr = f (t), решенного в 1922 г. в замкнутой форме Т. Карлеманом [1], интегральные уравнения первого рода с логарифмическими особенностями постоянно привлекали внимание исследователей теории краевых задач аналитических функций и сингулярных интегральных уравнений. В дальнейшем были получены многочисленные результаты, относящиеся к исследованию и решению различных типов уравнений с логарифмическими особенностями в ядре, исследованию свойств интегральных операторов с логарифмическими особенностями в различных функциональных классах и пространствах (ссылки в [2]). При изучении сингулярных интегральных уравнений с логарифмическими особенностями рассматривались классы или пространства первообразных либо от гельдеровских функций [3, 4], либо от функций из лебеговских пространств [5], а также функций из этих классов, имеющих степенные особенности в отдельных точках.

В работе [2] было предложено и исследовалось в гельдеровских классах функций «модельное» интегральное уравнение первого рода с переменной логарифмической особенностью в ядре вида:

b                                  т

| ^ d ^ = f ( t ) -                   (1)

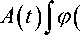
• т) dT + B (t )J ф(т) dTJ

t                     Г           a

Здесь Г = [ a ; b ] - простая ориентированная кривая на комплексной плоскости с концами a и b (ориентация от а до b ; возможно a = b ). В работе [6] это уравнение исследовалось в лебегов-ских классах функций.

В связи с теорией краевых задач и сингулярных интегральных уравнений со сдвигом [7-9] представляет интерес изучение интегральных уравнений с двумя логарифмическими особенностями в ядре, одна из которых получается из другой в результате сдвига. Как обобщение уравне- ния (1) на случай двух «подвижных» логарифмических особенностей, содержащихся в инте гральном уравнении, можно рассмотреть в качестве модельного уравнение

b                     b

A ( t ) j ф ( т ) d T- g ( t ) | ф ( ^г ) d T

< а — 1 ( t )                           t

+ B(t)ф(т)dT  j}^d^-j g(^p(^ d^ = f (t). (2)

Г             a              a

г

a

Это уравнение связано с линейным функциональным уравнением

(Fg M)( t)5 vИ. t))- g(t )v(t)=h(t) •

Имеется большое количество публикаций, связанных с уравнением (3) и его обобщениями [10]. В [10] исследования проводились в классах непрерывных функций.

В работе исследуются свойства решений уравнения (3). Цель статьи - найти условия существования и единственности решения уравнения (3) в классах Ap первообразных от лебеговских функций, если коэффициент и правая часть также принадлежит Ap . Эти условия зависят от значений коэффициента g (t) уравнения на концах кривой. Показано, что если коэффициент и пра вая часть уравнения (3) принадлежат Ap , то и решение принадлежат Ap .

Обозначения и вспомогательные утверждения

Класс непрерывных на Г функций обозначим C ^г или просто C . Класс функций ф , удовлетворяющий условию Гельдера на Г :

Iф(ti)-ф(t2)| 1.

p                  pq

1 < q <  p

Пусть а = а ( t ) , t е Г - отображение кривой Г на себя со свойствами:

• 1.    а - взаимно однозначное непрерывное отображение кривой Г на себя с сохранением принятой на Г ориентации;

• 2.    На Г не существует других неподвижных точек (н.т.), кроме а и b ;

• 3.    Для всех t еГ существует а '( t ) ^ 0, причем а е Н ₆ на Г , 0 е ( 0;1 ] ;

• 4.    | а ^г( a )|^ 1, | а '( b )| ^ 1.

Будем применять обозначения: а ₀ ( t ) = t , а ₁ ( t ) = а ( t ) , а _п ( t ) = а ( а _{п - 1} ( t ) ) , а _{- 1} ( t ) - обратное к а отображение, а - n ( t ) = а _{- 1} ( а - n _{+ 1} ( t ) ) , n = 1, ^ . Очевидно, а _п ( а - n ( t ) ) = а - n ( a n ( t ) ) = t .

Если для всех t е ( a;b ) а ( t ) е ( a ; t ) , то точку а будем называть притягивающей неподвижной точкой (п. н. т.). Если для всех t е ( a;b ) а ( t ) е ( a ; t ) , то точку b будем называть отталкивающей неподвижной точкой (о.н.т.). Очевидно, что всегда либо точка a - п. н. т., а точка b - о. н. т., либо наоборот, a - о. н. т., а точка b - п. н. т.

Всюду в работе полагаем, что a - п. н. т., а точка b - о. н. т. В этом случае условие 4 можно заменить на условие

4*. | а '( a )| <  1, | а '( b )| >  1.

Заметим, что все утверждения, относящиеся к о. н. т., следуют из соответствующих утверждения для п. н. т.

Пусть c е ( a;b ) . Введем обозначение: I n ( c ) = [ а _п ( c ) ; а _{п - 1} ( c ) ] , n = 1, ^ .

Критерий Ф. Рисса принадлежности функции классу Ap, p > 1 для действительных функций, заданных на отрезке действительной прямой, имеет место в рассматриваемой ситуации, то есть для комплекснозначных функций на простой гладкой кривой, заданной на комплексной плоскости. Сформулируем его в виде следующей леммы.

Лемма 1. Пусть Г = [a; b] - простая гладкая кривая. Определенная на Г комплексная ком плекснозначная функция ф е Ap, p > 1, тогда и только тогда, когда для любой последовательности точек на Г  {tj, j = 0,...,n: t0 = a, tn = b, tj е(tj-1;tj+1), j = 1,...,n -1}

|^ф ( t j + 1 ) ^{- ф} ( t j )| p j ^j j

I p ^{- 1}

< K ,

где постоянная K не зависит от {tj, j = 0, n }.

Основные результаты

Введем обозначение

G n ( t ) =к g(a¹, ) ) - G o ⁽ t ) * 1 G - n ( t ) =n g ⁽ b\ • n = ¹’ “ ■             ^<4)

j = ⁰ g ⁽ a )                              j = i g ( a — j ( t ) )

Сначала сформулируем две теоремы, относящиеся к полуоткрытым промежуткам гладких кривых.

Теорема 1. Пусть h,g еH^, g(t)^0, t е[a;b). Пусть |g(a)| > 1. Тогда существует единствен ное решение уравнения (3) в классе C[a;b) [10]:

V ⁽ t ) =

ГО

- 2

к = 0

h(ak (t)) п g (aj (t))

” h (ak(t))

^k = ⁰ g ^{k + 1} ( a ) G k + 1 ( t ) ■

<5)

Если g , h е A [ pa ^{; b} ) , p >  1, то V е A pa ^{; b} ) .

Введем обозначения. Пусть точка c е ( a ; b ) - произвольна; обозначим через C_c , _g , h класс функций f , непрерывных на 1 ₀ ( c ) = [ a ( c ) ; c J и удовлетворяющих условию:

f (a(с))-g (c) f (c ) = h (c) ■

Пусть K - произвольный класс функций; положим по определению:

^K c , g , h = C c , g , h ^ ^K ■

Теорема 2. Пусть c е(a;b)  - произвольна;   v0 е Cc,g,h   - произвольна. Пусть h,g е HM, g(t)* 0 t е(a;b]. Пусть |g(b)| > 1. Тогда уравнение (3) разрешимо в классе C(a;b]. Его общее решение имеет вид:

(К\ ^h ( ^b )

^{V ( b} ) = i - T c b ) ’

П g ( ^a j - n ( t ) ) v 0 ( ^a - ,, ( t ) ) + j h ( ^a k - ,, ( t ) ) П g ( a - n ( t ) ) , t ^е I n ( c ) , ⁿ = ^2:3:". j = 0                                 к = 0               j = к + 1

g ( ^a - 1 ( t ) ) V 0 ( ^a - 1 ( t ) ) ^{+ h} ( ^a - 1 ( t ) ) , t ^{е 1} 1 ( ^c ) ,

<6)

V 0 ( t ) , t ^е I 0 ( ^c ) ,

П g ^{- 1} ( ^a j - n ( t ) ) V 0 ( ^a n ( t ) ) ^- j h ( ^a n - к ( t ) ) fl g ^{- 1} ( ^a n - j ( t ) ) , t ^{е 1} - n ( ^c ) , ⁿ = 1;²;- j = 1                                    k = 1                j = к

Если Ц <  log ^ ,( a ) | g ( ^a )| , то / G H Ц ’ b ] . Если g , h G A ( a ^; b ] , P >  1 ,   / 0 ^G A Pab ] _g , h, P 0 >  ¹ , то

/GAPa;b] для Рь=min{a;Po;p*b},pb=(1 -logиь)g(b)l)  , если g(b)

Следующая теорема является следствием теорем 1 и 2.

Теорема 3. Пусть h,g gНц, g(t)*0, t g[a;b]. Пусть |g(a)| > 1, |g(b)| > 1. Тогда существует единственное решение уравнения (3) в классе C[a;b] (b0). Оно определяется формулами: , . h(a)         , .                 h (ak (t))

u(a, Y(t) = "^/ (   k+v   ( V tg(a;b]■

^{1 g (a})             ^k=⁰(g (^a))   Gk+1 (t)

Если ц< loga>_(a) |g(a)|, то / g HЦ^;b^]■

,             ,      ,[a;b]       . , P-1    ,            i м                 Ja;b]

Если g, h G AP , P > 1, —— < log|a(a) |g (a)|, то / g ap■

Теорема 4. Пусть h, g g Нц , g (x )^ 0, x g[ a; b ]. Пусть |g (a )|> 1, |g (b )|< 1. Тогда для существования решения уравнения (3) в классе C[a;b] (b0) необходимо и достаточно, чтобы выполнялось условие

“      h (а (t)).

У -----У k ----= 0, t g (a;b)

k +1

k=-»( g ( a ))   Gk+1 ( t )

При выполнении (7) решение уравнения (3) единственно, причем / g нЦ^1;b]. Если g, h G AP;b^], P > 1, то / G AP;b^]■

Замечание. Если g(a) = 1, |g(b)| > 1 или |g(a)| < 1, |g(b)| > 1, то решение уравнения (3) не единственно. В первом случае решения существуют тогда и только тогда, когда h (a) = 0, а общее решение является однопараметрическим семейством функций. Во втором случае уравнение (3) имеет континуум линейно независимых решений в классе непрерывных на [a;b] функций. В работе эти случаи не рассматриваются.

Доказательство теоремы 1

Сформулируем несколько вспомогательных утверждений.

Лемма 2. Пусть Г = [a;b] - гладкая в некоторой окрестности точки a кривая, r - действительное число, такое что

| a'( a )| < r< 1.

Тогда: существует такая окрестность V (a) точки a на кривой Г и такое натуральное число N, зависящее только от r, что для любых точек t1,12 g V (a) и любых целых m, n > N

|an (t1) - am (t2 )| < r\«n-1 (t1) - am-1 (t2 )|, существует число K такое, что для любых точек t g V (a)

|«n (t)^{- a}| < K1 rn ■

Следствие. В условиях леммы 2 для k = 0;1;2;...

| «k (t1)^-«k (t 2 )| < rkt1 ^-t 2| ■

Лемма 3. Пусть Г = [аb] - гладкая в некоторой окрестности [ас] точки а кривая, функция g(t)^ 0, g(t)е Hm, t е[ас]. Тогда последовательность {Gn (t), n = 1;2;...}равномерно сходится на [а; с ], lim Gn (t ) = Ga (t )* 0, ro. n ^ro

В частности, если функция g непрерывна на [ab), то и G_a (t) непрерывна на [ab); G_a (а) = 1.

Сформулируем неравенство Гельдера для числовых рядов в форме:

Лемма 4. Пусть {aj, j = 0;1;2;...} и {bj, j = 0;1;2;...} - последовательности действительных чисел, a

. Пусть сходятся ряды p1 £ b^ = Gp-1, j=0

ro(a -Y у - . ^ b,

Тогда сходится ряд £ а,, причем j=0

p го ]

Y aj I

го

aj

j=01 ^b

.

Доказательство теоремы 1.

Шаг 1. Пусть с е(a; b), f e

p

на [а;с], f (а)| < 1. Тогда

j

Пf (ак (t))е A(P,L), к=0

где постоянная L не зависит от j .

Доказательство шага 1. Из условия следует, что существуют число r1 и отрезок [а; с1 ] с [а; с] такие, что для t е[ а; с1 ] |f (t )|< r1 < 1. Существует    к0 е{0;1;2;...} такое, что для к ^ к0 f (ak(t)На ; с1 ] и, следовательно,

| f («к (t))|< Г1 < 1, если t е[а;с].(9)

Из условия f е AP на [а;с] и леммы 1 следует, что если {t0;...;tn } с [а;с], 10 = а; tn = с, то у |f (tm+1 )- f (tm )|P p-1

m=0    |tm+1

где M не зависит от выбора {t₀;...;t_n }. Из следствия леммы 2 тогда следует:

А |^f(«к⁽tm+1))^{- f}(«к⁽tm ))|^P   А |^f(«к⁽tm+1)) ^{- f}(«к⁽tm ))|^P |«к (tm+1)^-«к (tm )|^P-1

m=0

^P-1

Г m+1   ^m |

m=0

| «к ( tm+1)- «к ( tm )|^{P 1}

p

I^p-1

Г m+1   ^m |

Пусть |f (t)| < M1 на [а;с] для некоторого M1. Очевидно,

^к0 ^-1

П f («к (t))^ Mк0.

к =0

j

Докажем, что для П f (^ак (t)) выполняется условие леммы 1.

к=0

j

j

p

j

j

p

n

Z

m=0

k=0

_________k=0

Ip-1 r m+1   mn\

n

< Mk0 Z m=0

П f (ак (tm+1)) - П f (ак (tm ))

k=k0

k=k0

I^p-1 r m+1    m |

<

(следует из (11))

n

M1k0 Z m=0

j                                         l-1                   j

Z( f (al ( tm+1 ))-f (al ( tm )))П f (ak ( tm )) П f (ak ( tm+1 ))

p

k=10

Ip-1 r m+1   mn\ l0-1      j

k=l+1

<

(для удобства записи формул считаем, что П, П равны 1)

l0      j⁺¹

n

Mk⁰Z m=0

^jp-1 Z |(^f (^al (tm+1)) ^{- f} (^al (tm l=10

I^p-1

Г m+1    m |

p

I jk⁰

-----<

(здесь использовано (9) и неравенство

j

Mk0 Z ' l=0

n

:p-1Z xf, ii i=1

np

Z^ ^f(^al (tm+1))- ^f(^al (tm )))| ■ p-1 rj - ^k0 m=0

Z Xi

I^p-1

Г m+1   mn\

< M^k0M j^p-1r ^k0Z^rl^(p 1) < l=0

(здесь использовано неравенство (10))

Mk0 M j^{p -1}r -^k(

^:0S, S = Z rl^(p-1)

TO

.

l=0

j где L = MM" M2 S и

Пусть max{jp 1 r/ ^, j = 1;2;...}= M2. Тогда  П f (ak (t))e A(p,L), k=0

не зависит от j .

Шаг 2. Подготовимся к проверке выполнения критерия Ф. Рисса (лемма 1) для функции (6). Введем обозначение для удобства записи формул:

Hj( t ) =

g'*' (a)G,+1 (t)

-—¹----, j = 0;1;

П g ^(ak⁽t))

k=0

,

где Gj (t) определено формулой (4). Так как |g¹(a)| < 1 и g¹(t)e Ap, то, как следствие первого шага,

Hj e A ( p, L ), причем L не зависит от j. По лемме 3 функция Hj равномерно ограничена по j на [a; c], то есть существует число M3 такое, что H (t)| < M₃ на [a;c] для всех j = 0;1;.... Используя обозначение (13) и формулу (5), запишем:

n

Z

У ( tm+1 )^-^ ( tm )| p _n

m+1   tm|           ^m =0

TO

Z(h (^aj (tm+1 j=0

I^p-1

I tm+1    tm|

p

< S' + S2,  (14)

где

n

S1 = 21—p E m=0

w

E h (^aj (tm+1 ))(Hj (tm+1 )- Hj (tm ))

j=0

m+1  tm

n

< 21-p E m=0

w I /

E h (aj (tm+1

V j=0

p

w

I^p—1

Г m+1   mn\

,

p

n s2 = 21—p E m=0

j=0

I^p—1

Г m+1   ^m|

w

p

n

< 21-p E m=0

I^p—1

I tm+1    tm|

,

причем неравенство (14) следует из неравенства (12) при n = 2, а неравенства (15) и (16) верны, если ряды из модулей в их правых частях сходятся, что будет показано ниже.

Шаг 3. Рассмотрим частный случай, когда h (a) = 0.

Оценим слагаемое S . Временно обозначим:

p-¹j

^-j = |h(«j⁽tm ))(Hj⁽tm +1) ^-Hj⁽tm ))|, vj = r 2p  •

Так как h (a) = 0 по предположению и h e A_p c H_p-3, то

p p —1

|^h(^aj (tm ))| < |h(^aj (tm )) ^{— h}(^a)| < ^M4 ^j (tm ) ^{— a}| p

для некоторой постоянной M₄. Используя обозначения (17), неравенство H (t)| < M₃ для всех j = 1;2;3;... на [a;c], неравенство (18) и лемму 2, получим:

u

—< vj p-i

p-1                 ^{p-1  p-1} -

^2M3^M4 ^aj (tm)^-a\T  2M₃M₄K ^pr ^p       p-^{1 j}

-------!---<---3—⁴----------< M5 r^{2 p} ,

vj

vj

w

где M5 = 2M3M4K ^p ,

uj постоянная K введена в лемме 2. Поэтому ряд E — V;

^p сходится, что

доказывает неравенства (15) и (16). Неравенство (8) леммы 4 в обозначениях (17) имеет вид:

w

E-

V j=0

w

p

w

w          w

< G E-j  = G GE j=0 V vj J      j=0

|h(aj (tm ))(Hj (tm+1 )- Hj (tm ))|p

j=0

r

Используя обозначения (17) и неравенство (19), получим:

w

E r

n

S1< 2^1—pG E — m=0

h (aj (tm ))(Hj (tm+1) — Hj (tm ))p

I^p—1 r m+1 mm\

.

TO

Z r

n

2^1—pgZ 2=1_ m=0

(Kr )p|H(t„+1 ) — H(tm )p

<

I^p—1 гm+1   ^ml

2^1—pGK^p—1£ r j=0

/(p—) n-. | Hj ( tm + ) — Hj ( *„ )

m=0

I tm+1

-t I p^—1 m

p

- < 21—pGKp—1L £ j=o

= K1

Сумма S₁ оценена константой, обозначенной K₁ .

Оценим слагаемое S₂ . В этом случае временно обозначим:

uj = |h(“j (tm+1

Тогда из леммы 2 и h е H _p—1 следует: ^p

,vj

— j

2p

Uj ^M 4 ^aj- ( tm+1)

vv

—

p^—1 «j⁽tm )| p

—j < M 6 r^{2 p}

.

Применяя неравенство (8) леммы 4, оценим S2 точно так же, как S1. Пусть S2 < K2. Следовательно, для функции у , заданной формулой (5), n z j=0

V (tj+1) ^—У (tj )| p

I tj+1 -,r¹

откуда в силу леммы 1 у (t )е Ap, t е [а; c ].

Шаг 4. Пусть теперь не обязательно h(а) = 0. Очевидно, уравнение (3) равносильно уравнению

x(« (t)) —g (t) X (t ) = hl (t) , где

X( t )=V (t)—1^^' h1(t)=h (t)—14^(0)(1—g(t)).

Так как h1 (а) = 0, x(t)e A_p, t е[а;c], а, следовательно, у (t)е A_p, t е[а;c], что завершает доказательство теоремы 1.

Приложение к сингулярным интегральным уравнениям

Рассмотрим уравнение (2). Воспользуемся формулой перестановки порядка интегрирования в повторном интеграле [7]:

J ф(т) dr J p^) d^ = J p(£) d^J ф(т) dr .

Г         а ^ t      Г ^ t ^

Здесь Г = [a;b] - простая гладкая кривая, внутренний интеграл в левой части при t е (а;т) и интеграл в правой части существуют в смысле главного значения, а внешний интеграл левой части существует по крайней мере как несобственный. Из формулы (20) следует

Лемма 5. Пусть Г = [а; b] - простая гладкая кривая, c е(а; b). Пусть функция ф интегрируема по Лебегу на [c; b], причем

b

V (t) = J ф (т) dr е H[c;b],

t

Дильман В.Л.,                           Условия существования и единственности решений

Комиссарова Д.А.                                  линейных функциональных уравнений … функция p е H[c’b], а функция а задана на Г = [а; b ] и удовлетворяет условиям 1-4. Тогда b       "'ё) рe)      b р(^     b

Jф(т)dT J —— de = J ——de  J ф(г)dr, t e(a;b).             (22)

c           а(c) ⁵t        а(c) ⁵t     a_j(5)

Здесь внутренний интеграл в левой части при t е (а(c);а(г)) и интеграл в правой части сущест- вуют в смысле главного значения.

Переходя в (22) к пределу при c ^ a, получаем:

J фТ) dT J) 0 de-f 0

b de J ф(т)dr,  t е(a;b).

^а-1^(e)

Из (20) и (23) следует:

J фТ) dT J p^ de - Jg^^ de -J p⁵ de  J фТ) dT - g (t )/фТ) dr .

Г         ( a ^et      a ^et       Jr ^et    (а,^t)                 t         ,

Тогда (2) приобретает вид:

( b

b

\

A(t) J ф(т)dr-g(t)Jф(т)dT + B

l ^а-1⁽t)

t           J

j ;e

b

b         )

de J ф(т)dr-g(t)Jф(т)dT -f(t)

l ^а-1⁽t)

t           J

или

A(t )k(t) + B(t)J p((V(e) de - f (t),(24)

Г ^{e 1}

где обозначено:

то есть (см. (21))

bb

J ф(т)dT-g(t)Jф(т)dT = v(t), а-1(t)

^(а-1 (t))- g(t)^(t) = V(t) .

Поэтому для решения уравнения (2) следует решить сингулярное интегральное уравнение (24), полученное решение подставить в правую часть функционального уравнения (25); решение этого уравнения, в соответствии с (21), продифференцировать. Если решение уравнения (24) принадлежит L_p, p > 1, то решение уравнения (2) также принадлежит L_p .