Актуальной задачей математического моделирования является задача описания динамики численности популяции. Одним из свойств решений моделей, описывающих динамику численности популяции, является отделённость решений от нуля при определённых сочетаниях параметров модели, что обеспечивает выживание популяции. Знание функциональной связи между нижними оценками решений и параметрами моделей позволяет делать выводы о развитии популяции в будущем, не находя решений в явном виде.

Модель Николсона

Модель Николсона [1] динамики численности одной популяции описывается дифференциальным уравнением с запаздыванием г > 0:

^ = Р-х(г-г).е-“л(/-г)-^), />0,                   (1)

dt

x(s) = Ф^ для 5 е [-г, 0],                                 (2)

(деС([-т,0],7?+) и р(0)>0, где х^ - численность популяции в момент времени t; Р>0 - коэффициент рождаемости; т > 0 — время созревания особи; а > 0 - коэффициент системы; 3 > 0 - коэффициент смертности; ф^ - начальная функция.

При исследовании решений моделей, описывающих численность популяции, важной задачей является определение условий равномерной отделённости решений от нуля, что обеспечивает сохранение популяции [2]. При различных сочетаниях параметров уравнения Р,8 найдены пока затели живучести популяции в виде функции л(Р>8).

Теорема 1. При 3 <Р<Зе для любого решения х^ задачи (1)—(2) верно равенство

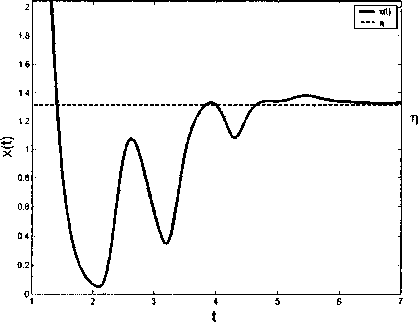
Рис. 1. Отделённость от нуля устойчивого решения модели с параметрами из первой части теоремы 1

lim infx(Z) = 7? = —1п| — |.             (3)

<->оо              а \8 )

При Р> Зе для любого решения т(/) модели (1)—(2) верно неравенство

/>2 - — lim inf х^ >г]= —— е 8е.         (4)

аЗ^е

Таким образом, условием выживания популяции в данной модели является выполнение неравенства Р>3.

На рис. 1 представлено устойчивое решение модели Николсона с параметрами, соответствующими первой части теоремы 1 (сплошная линия), а также найденный теоретически показатель живуче- сти т] (пунктирная линия). С течением времени решение стремится к показателю г;.

На рис. 2 представлено неустойчивое решение модели Николсона с параметрами, соответствующими второй части теоремы 1. С течением времени решение становится больше найденного теоретически показателя живучести ту.

Двухзонная модель

Двухзонная модель, построенная на основе модели Николсона, описывает динамику численности рыбной популяции, находящейся в двух относительно изолированных зонах, причём рыбалка разрешена только во второй зоне. Рыба может мигрировать из одной зоны в другую. Данная модель описывается системой двух уравнений с запаздыванием [2]. Эта модель принадлежит классу нели-

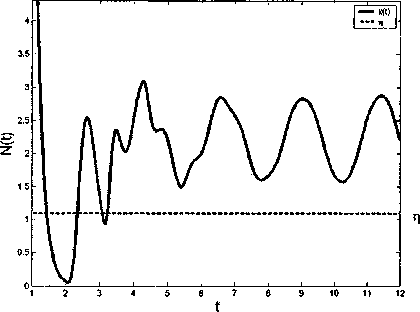
Рис. 2. Отделённость от нуля неустойчивого решения модели с параметрами из второй части теоремы 1

нейных уравнений с запаздыванием и выглядит следующим образом:

^^ = -Ш] •х1(/)-<71 ■х1(/) + 2 "^(O + Zr^i^-7)^ “'^^ г\

^™ = -^2 • ^2(0-^2 • ^2 W + d_vx_x(t) + y₂-x₂(t-T)-е"“^тХг-h-x₂ (О, I at

х\$> = ф^ для se[-r,0], z = l,2,

Ф 6 С([-т, 0], R+) и (9(0) > 0, где X] (?), х2 (0 - численность популяции в момент времени t; mx > 0, m2 > 0 - коэффициенты смертности; /, > 0, у2 > 0 - коэффициенты рождаемости; ах > 0, а2 > 0 - репродуктивная сила; dx > 0 - коэффициент миграции рыбы из зоны 1 в зону 2; d2 > 0 - коэффициент миграции рыбы из зоны 2 в зону 1; И > 0 - коэффициент рыбалки в зоне 2; т > 0 - запаздывание, связанное с воспроизводством популяции.

Будем иметь в виду, что индексы 1 и 2 обозначают зоны 1 и 2 соответственно.

Для сохранения популяции необходимо, чтобы

3// > 0 lira inf Xj (f) > ц, i = 1,2.                                  (7)

/—>co

Но для того чтобы судить о выживаемости, необходимо знать показатель живучести // как функцию от параметров уравнения jii(m_x,m₂,у_х,у₂, d_x,d₂,a_x,a₂,h).

Для задачи (5)-(6) доказана следующая теорема.

Теорема 2. Для всякой траектории системы (5) с положительными начальными условиями выполняются неравенства:

1)При m_x+d_x<у_х< (m_x+d_x)e, m₂+d₂ + h < у₂< (m₂ + d₂ + h)e

lim inf xx(t) > р.х. lim infx2(/)^ Ц^. t-yn (8) 2) При ух > (т, + dx )е, у2 > (т2 + d2 + А)е lim inf хх (f) > //3, /—>00 lim inf x2^> Цд. (9) 3) При тх *dx <ух< {mx+dx')e, у2 > (m2+d2 lim inf xx (0 > jUx, t-^x + h)e lim infx2(/)> цд. <->CO (10) 4) При ух > (mx + dx )e, m2 + d2 + h < y2 < (m2 + d2 + /z)e lim inf Xj (?) > /z3,    lim inf x2 (/) > //2, (H) где

Хохлов А.Д.

//, = —In——— > 0, / = 1,2,

• a, т_х + d_x

  
  

  ^/ =-------"-----:

  “j^j^dj^

  
  

  Т^е

  
  

  ^j-vdjV _>Q, y _{= 3)4}

  
  

Теорема 2 определяет функциональную связь между коэффициентами живучести популяции в обеих зонах и параметрами системы. Это позволяет, не решая уравнения, а зная только его параметры, определить, выживет популяция в будущем или нет.

На рис. 3 и 4 представлены фазовые траектории решений задачи (5)-(6), параметры которой удовлетворяют условиям теоремы 2.

На рис. 3 изображена траектория устойчивого решения (со следующими параметрами: т_х = 0,2, т₂ = 0,5, у_х = 3,3, у₂ = 3,7, d_x = \,d₂ = 1, а_х = 0,16, а₂ = 0,9, h = 0,7 ), а на рис. 4 (с параметрами: т_х = 0,2, т₂ = 0,5, у_х = 2,2, у₂ = 13,7, d_x = 1, d₂ = 1, а_х = 0,16, а₂ = 0,9, h = 0,7 ) траектория неустойчивого решения модели. На графике показаны две прямые, представляющие показатели живучести для первой и второй зон соответственно. В обоих случаях наблюдается отделённость решений от нуля независимо от устойчивости.

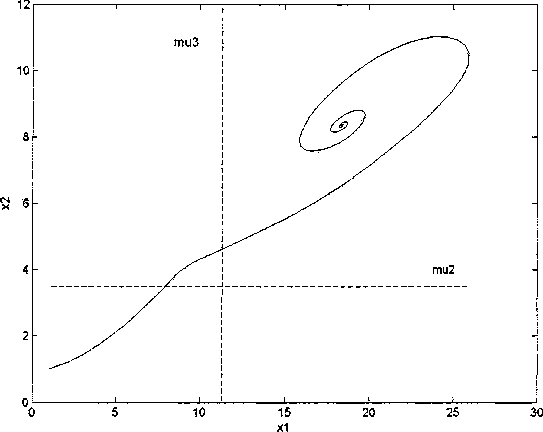
Рис. 3. Отделённость от нуля устойчивого решения модели с параметрами из п. 4 теоремы 2

Вывод

Для двух моделей представлены условия равномерной отделённости решений от нуля, а также найдены показатели живучести как функции от параметров моделей. На приведённых графиках можно проследить поведение решений моделей относительно найденных показателей живучести. Полученные результаты имеют прикладное значение и могут быть применены для анализа численности популяции.

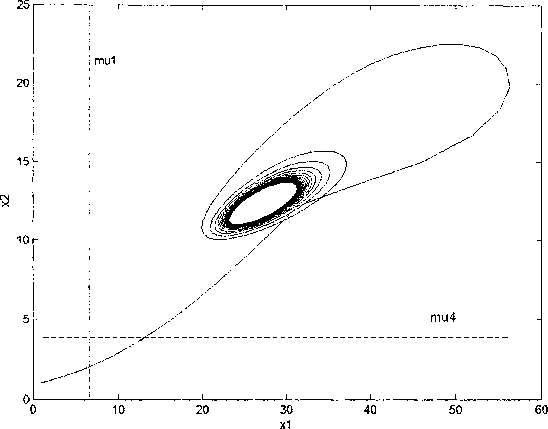
Рис. 4. Отделённость от нуля неустойчивого решения модели с параметрами из п. 3 теоремы 2