Установившиеся вынужденные колебания системы твердых тел, установленных на упругом стержне

Для вывода уравнений движения систем твердых тел, установленных на упругом стержне, используется вариационный принцип Гамильтона, который справедлив, как для систем с сосредоточенными, так и для систем с распределенными параметрами. Полученные на основании принципа Гамильтона, уравнения движений таких механических систем являются гибридными системами дифференциальных уравнений [1–3]. Под гибридными системами дифференциальных уравнений понимается система дифференциальных уравнений, состоящая из обыкновенных дифференциальных уравнений и уравнений в частных производных. В работе [4] была предложена обобщенная математическая модель балки Эйлера – Бернулли с закрепленными краями и прикрепленными на нем с помощью упругих связей произвольной системы твердых тел, соединенных между собой упругими связями. Обобщенная математическая модель таких механических систем, описывается системой гибридных дифференциальных уравнений [4]:

' Az + Bz + C ( Dz - u ) = 0,

d d               i

k .2 < x , t ) + b     ⁽ x , t ) = Z q_t ⁽ d ^{z (} t ) ^- u ⁽ x , t^{)) 5 (} x ^- a i ),

.  ^d t               ^d x             i = 1

где z(t) - n-мерная вектор-функция; u(x, t) - скалярная функция; u (t) - m-мерная вектор- функция с компонентами u(a1,t),•••,u(am,t); A, B - заданные, постоянные n x n - матрицы;

C - заданная, постоянная n x m - матрица; D - заданная, постоянная m x n - матрица; di - n-мерный вектор, составленный из строк матрицы D; k, b, ai, qi, (i = 1, m)

заданные

постоянные, причем 0 <  a i <  l ; штрих ()' - здесь и ниже операция транспонирования.

На функцию u ( x , t ) в зависимости от условий, накладываемых на правый и левый конец балки, задаются те или иные граничные условия. В частности, в случае жесткой заделки на концах имеем

u (0, t ) = 0, — (0, t ) = 0, u ( l , t ) = 0, — ( l , t ) = 0. d x                     d x

В данной работе развивается единый подход к построению амплитуд вынужденных колебаний системы, основанный на рассмотрении обобщенной математической модели (1).

1.    Гармоническое силовое возмущение, приложенное к системе твердых тел

В случае действия на систему неконсервативных сил вариационный принцип Гамильтона может быть выражен следующим соотношением

[ ^( T - U ) + 5(0 ) dt = 0

t 0

где Т - кинетическая энергия системы, U - потенциальная энергия системы, 5о - виртуальная работа неконсервативных сил.

Вывод уравнений движения конкретных систем на основании принципа Гамильтона (3) приведет к появлению в гибридной системе дифференциальных уравнений дополнительных слагаемых, соответствующих внешним неконсервативным силам. Если гармоническое возмущение частоты о приложено к одному или нескольким твердым телам системы, то в правой части обыкновенных дифференциальных уравнений обобщенной модели (1) появляются выражения вида H sin o t

Az + Bz + C(Dz - u ) = H sin ot, k ^rur(x, t)+b l-u(x, t)=Z qi(d1Tz(t)- u(x, t))5 (x - ai), о t           оx         *"7

где H - n -мерный заданный вектор.

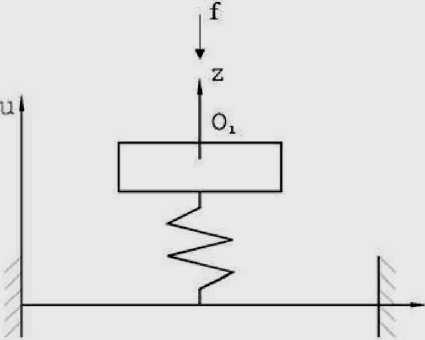
Действительно, для примера рассмотрим механическую систему, на массу т действует гармоническое силовое возмущение с частотой о и амплитудой f (рис. 1).

О           а             1

Рис. 1. Механическая система «твердое тело на упругом стержне» с гармоническим силовым возмущениям, действующим на массу

Для данной системы имеем:

• 1.    Потенциальная энергия пружины пропорциональна квадрату ее линейной деформации

• 2.    Кинетическую энергию твердого тела можно записать в виде суммы кинетической энергии поступательного и вращательного движений:

• 3.    Выражения для кинетической и потенциальной энергии стержня имеют вид:

U — c(z - и(a, t))2 1               2,

т - mz I I^(p

T\           +

1    22

где I - момент инерции твердого тела относительно центра масс при повороте на угол ф .

• ¹               л²                        l         -12„ а²

т 1 f J ди 1 ,         1 fгт д и I л

F — — p F — ddx , U — — E EI —- dx ,

• ²    20     (5 t J     , ² 2 0     (5 x ² )

• 4.    Работа неконсервативных сил в данной системе определяется следующим образом

где p - плотность материала стержня, F - площадь поперечного сечения, E - модуль упру- гости стержня, 1 - момент инерции поперечного сечения стержня относительно нейтральной оси сечения, перпендикулярной к плоскости колебаний.

8о — f cos o t 8 z .

Учитывая, приведенные выше соотношения, можем найти вариацию функционала действия (3) в виде tГГ/

JI (-mz - c (z - и (a, t)) + f cos ot^z +

t 0

£

+

%                     „ д2и

J c (z - и (x, t)) 8( x - a)-pF—-0                                     512

-

д4и 1х л E1—- 8udx дx4 J

Таким образом, из (5), в силу независимости вариаций координат получим уравнение движения системы

mz + c ( z - и ( a , t )) — Hcos ^ t ,

2a      84a

p F ^ 4 + E1 ^ 4 — c ( z - и ( x , t )) 8 ( x - a ).

д t ²        д x ⁴

Вернемся к рассмотрению системы (4). Будем искать вынужденные установившиеся колебания системы (4) z ( t ), и ( x , t ) ввиде

z ( t ) — Z sin o t ,    и ( x , t ) — V ( x )sin o t ,

где o - частота внешних возмущений, Z - n- мерный вектор амплитуд вынужденных колебаний тел, V ( x ) - амплитуда вынужденных колебаний точек упругого стержня,

Подставив в систему (4) z ( t ), и ( x , t ) в виде (7) после преобразований получим алгеброиче-ско-дифференциальную систему

'( - o ² A + B + CD ) Z - CV — H ,

-o ² kV ( x ) + b ^{d V ( x} ) — У q ( d" Z - V ( x )) 8 ( x - a , ), .                dx     t!

где V - m -мерныйвекторс компонентами V ( a 1 ), ^ , V ( a m ).

В силу граничных условий (2) функция V ( x ) должна удовлетворять условиям dV    dV

V (0) — V ( l ) — 0, dV (0) — dV ( l ) — 0.

dx     dx

Отметим в [4] было показано, что решение V ( x ) дифференциального уравнения из системы (8), удовлетворяющее условиям (9), при любом Z удовлетворяет соотношению

m

V ( x ) — £ G , ( x - a , ) q_v(d i Z - V ( a^ .

I — 1

Пусть, при заданном значении и г (частота внешних возмущений), в соответствии с [4], найдены обобщенные решения G ₁ ( x ), G ₂ ( x ),..., G_m ( x ) уравнения

—го 2 kG ( x ) + b d G,(. x ) = 3 (x ), dx 4	(i = i,.	.., n ),	(11)
удовлетворяющие краевым условиям Г G , ( — a^ = G , ( l — a^ = 0,
‘ dG , x dG, „    x A ( — a ) = "^( 1 — a ) = 0. 1 dx         dx	( i = i,..	., m )	(12)

Принимая в (10) последовательно значения x = a_i, x = a ₂,..., x = a m , получим систему линейных алгебраических уравнений относительно V ( a ₁ ), V ( a ₂ ),..., V ( a_m ) . Объединив полученную систему с алгебраической системой из (8) получим линейную, неоднородную алгебраическую систему уравнений относительно вектора амплитуд Z и V

\— 6 ² A + B + CD ) Z — CV = H , NZ — MV = 0.

Здесь матрицы M , N определяются следующим образом

M = ' i + Gi(0)qi Gi( a 2 — ai) qi G2 (ai — a 2) q 2..... i + G2(0) q 2........ .....Gm (ai — am ) q.  " Gm (a2 — am )q. ...................... I Gi( am — ai) qi G2( am  a 2) q 2..... ................................ i + Gm (0)qm   , mmm

E G ⁽ a i - a ) q d I E G ⁽ a i - a ) qd 2...... E G ⁽ a i - a ) q d

	i = i m	i = i m	i = i
N =	E G , ( a 2 — a ) q , i = i	d i i E G , ( a 2 — a ) qd 1 = i	2...... E Gi ( a 2 — a i ) qd n i = i

E g ( a , — a , ) qd’ E g , ( a . — a , ) qd 2...... E ' V a . — a ) qd.

v i = i                                  i = i                                     i = i                              /

Отметим, если, частота внешних возмущений не совпадает с какой-либо собственной частотой, тогда определитель системы (13) не равен нулю

A = det

— I

■ 6 9 ²

A + B + CD

N

—

^ 0.

M )

Решив линейную систему

алгебраических уравнений (13) найдем n-мерный вектор амплитуд вынужденных колебаний масс Z , и амплитуды вынужденных колебаний точек крепления упругих связей к стержню V(a1),V(a2),..., V(am) . Амплитуды вынужденных колебаний произвольной точки x стержня найдутся по формуле (10).

■ ■

- mz t 0

I

- c ( z - u ( a , t ) ) ) 5 z + J ( c ( z

- u ( x , t ) ) 5 ( x - a ) +

+ f cos ю t 5 ( x

a ^u a ^u i

- a, - p F —-e EI     o udx

¹⁷         a t ²         a x ⁴ J

dt = 0.

Таким образом, из (14) получим уравнение движения системы mz + c (z - u (a, t)) = 0

<

^a i ) .

„ a2u      a4u pF dp + EI dp = c (z - u (x, t)) 5 (x - a) + f cos юt5( x

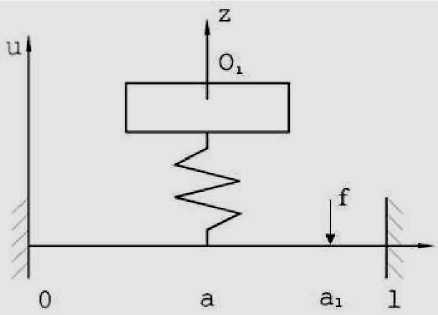
Рис. 2. Механическая система «Твердое тело на упругом стержне» с гармоническим силовым возмущением, действующим стержень

Поэтому, если на систему взаимосвязанных твердых тел, прикрепленных упругими связями к балке Эйлера - Лагранжа, действует гармоническое силовое возмущение с частотой го , приложенное в одной или в нескольких точках стержня, то в этом случае в правой части уравнений в частных производных обобщенной модели (1) появятся дополнительные слагаемые

Az + Bz + C (Dz - u) = 0, d u        d u       m 7ZT

<

k d"^ ( x , t ) + b    ( x , t ) = У q_t ( d z ( t ) - u ( x , t )) 5 ( x - a ) +

a t ²            a x ⁴         7=1

s

+У Hi sin rnt 5(x - a), i=1

где H i - заданные амплитуды внешних воздействий, приложенные в точке стержня с координатой a .

Подставив в систему (14) z ( t ), u ( x , t ) в виде (7) после преобразований получим алгебраическо-дифференциальную систему

( -ю ² A + B + CD ) Z - CV = 0

„            d 4V(x. 1    ™„

^ —ю2kV(x) + b----(-) = У qi(d ‘Z - V(x))5(x - ai) + ,(15)

dx sE

+ У H i 5 ( x - a i )

_ i = 1

где V - m -мерный вектор с компонентами V ( a 1 ), — , V ( a m ).

Рассмотрим вспомогательную краевую задачу для алгебраическо-дифференциальной системы (15) с граничными условиями (9).

Теорема 1. При любых значениях Z для обобщенного решения V ( x ) дифференциального уравнения

• - ю ² kV ( x ) + b d V ⁽ ₄ x ) = У q i ( d i ‘ Z - V ( x )) 5 ( x - a i ) +] T H i 5 ( x - a i ) (16) dx          i = 1                                            i = 1

справедливо представление ms

• V ( x ) = £ G i ( x - a^q_t(d i Z - V ( a i )) - V G ( x - a ) H i i = 1                                                           i = 1

  
  

где функции G i ( x ), ( i = 1,..., m ) обобщенные решения уравнений

-ю2kG (x) + b^ ^i(x) = 5(x),    (i = 1,...,m), i           dx4

с граничными условиями

G i ( -a^ = G i (l - a i ) = 0,

^G ( - a i ) = dG- ( l - a i ) = 0, ( i = 1,..., m ), dx        dx

функции G i ( x ), ( i = 1,..., s ) обобщенные решения уравнений

-ю2 kG( x) + b d G‘( x) = 3( x),    (i = 1,..., s), dx с граничными условиями

G i ( - a) = G ( l - a) = 0, ^G ( - a) = ^G ( l - a) = 0, ( i = 1,..., s ), dx        dx

Доказательство. Представим (17) в виде ml

V ( x ) = £J ( G ( x - £ ) q i ( d i Z - V ( £ ) -5 ( § - a^ ) d ^ +

I = 1 0 ^x

sl

+ £J G ( x - ^ ) H, 5 ( ^ - a) d ^ .

I = 1 0

Отметив, если функция V(x) обобщенное решение [5] дифференциального уравнения (16), то для любой компоненты v(•,•) основной вектор-функции (у(•), v(•,•)) е K, при любом t е[0,T]

справедливо тождество l.

j Л ² kV ( x ) + b 0 I

d ⁴ V ( x X) ,

———) I-v(x,t)dx = dx J

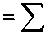
q i (d i Z - V ( a i )) v ( a i , t )

s

+E Hv (a, t), i=1

в справедливости представления (17) можем убедиться непосредственной подстановкой (18) в левую часть (17).

Пусть в соответствии с изложенным выше найдены обобщенные решения G 1 ( x ), G ₂( x ),..., G_m ( x ) и G 1 ( x ), G ₂( x ),..., G m ( x ) соответствующих уравнений, удовлетворяющие заданным согласно поставленной задаче краевым условиям.

Далее, принимая в (17) последовательно значения x = a 1 , x = a ₂ ,^, x = a m , получим систему линейных алгебраических уравнений относительно V ( a 1 ), V ( a ₂),..., V ( a m ) m

(1 + Gj (0)qjV(aj) + £G , (aj - a,)qV(a,)) = i=1, i * j(20)

= ]Г G(aj - ai)qidiZ + ]T G(aj - a)H, (j = 1,...,m). i=1

Используя матричные обозначения, систему (20) можно записать в виде

MV = NZ + b,(21)

где М и N матрицы, соответственно размерности m х m и m х n , такого же вида, как и в системе (13); b - m -мерный заданный вектор

У G,(a - a,)Hi i=1

s b =

У G , (a ₂ - a , ) H ,

.

i = 1

s

У G , (a m - a)H ,

Объединив (21) с алгебраической системой из (15), получим систему линейных неоднородных алгебраических уравнений относительно вектора амплитуд Z и V

(-- ( 2 ² A + B + CD ) Z - CV = 0, NZ - MV = - b .

Eсли, частота внешних возмущений не совпадает с какой-либо собственной частотой, тогда определитель системы (22) не равен нулю. Решив линейную систему алгебраических уравнений (22) найдем n- мерный вектор амплитуд вынужденных колебаний масс Z , и амплитуды вынужденных колебаний точек крепления упругих связей к стержню V ( a ₁), V ( a ₂),..., V ( a_m ) . Амплитуды вынужденных колебаний произвольной точки x стержня найдутся по формуле (17).

Заключение

В работе на основе обобщенной математической модели предложен общий численноаналитический метод нахождения амплитуд установившихся вынужденных колебаний систем взаимосвязанных твердых тел, прикрепленных упругими связями к упругому стержню (балке Эйлера – Бернулли). Предложенный метод полностью теоретически обоснован и может быть положен в основу алгоритмического обеспечения построения амплитудо-частотных характеристик системы.