Установление времени совершения преступления следователем по разности температур исследуемых объектов и окружающей среды

Раскрытие и расследование преступлений представляет собой сложную и многокомпонентную работу [1]. По существу, это процесс повышения вероятности установления истины по уголовному делу: Ртах ~ / ( ^ 1» ^х2» •• • ^п) , где p – кумулятивная вероятность установления истины по уголовному делу, зависящая от объема полученных доказательств, ( О < р < 1), х – величина доказательственной информации, содержащейся в конкретном доказательстве, полученном в результате соответствующего следственного действия – осмотра места происшествия, следственного эксперимента, опознания, допроса, очной ставки, обыска и т.д.

Каждая улика в данном случае имеет свое значение, а расследование начинается, как правило, с осмотра места происшествия. При производстве данного следственного действия необходимо собрать максимально возможное количество доказательств совершенного преступления.

Рассмотрим такой важный след на месте преступления, как температура. В криминалистическом чемодане, на наш взгляд, должны быть два градусника для измерения температуры, т.к. с помощью температуры возможно установить время совершения преступления.

Согласно ст. 73 Уголовно-процессуального кодекса Российской Федерации «Обстоятельства, подлежащие доказыванию», при производстве по уголовному делу подлежит доказыванию событие преступления (время, место, способ и другие обстоятельства совершения преступления). То есть в первую очередь не- обходимо установить максимально точно время совершения преступления.

Например, на месте совершения преступления находится труп, чья температура ввиду недавно наступившей смерти не понизилась до температуры окружающей среды, нагретые или охлажденные относительно внешней температуры предметы, это позволяет с высокой степенью точности определить момент совершения преступления с помощью проведения эксперимента, составления и решения подходящего уравнения.

В данном случае следователь одним градусником может измерить температуру трупа, а другим – температуру окружающей его среды в одно и то же время (допустимо использовать один градусник при оперативном измерении трупа и окружающей среды). Полученные результаты будут занесены в протокол осмотра места происшествия, после чего следователь либо самостоятельно, либо прибегнув к помощи специалиста решит соответствующую физико-математическую задачу, с помощью которой он установит время совершения расследуемого преступления. Однако для оптимизации времени расследования, на наш взгляд, желательно, чтобы подобную задачу по определению температуры следователь решал самостоятельно, что позволит по горячим следам сформулировать и начать проверку следственных версий, выявить несостоятельное алиби подозреваемых и т.д.

Условия задачи

Пусть у нас есть предмет с температурой л , помещенный во внешнюю среду с температурой Г2 , и при этом т, =г2.

Ясно, что со временем разность температур будет стремиться к нулю , наступит тепловое равновесие, когда        , тело с температу рой примет температуру окружающей среды, если нет источника, поддерживающего его температуру.

То есть существует строгая функциональная зависимость между разностью температур и временем. Ясно, что при возможны всего два варианта – либо        , либо        . При рас следовании преступлений следователь на месте происшествия обнаруживает труп, чья температура ввиду недавно наступившей смерти не понизилась до температуры окружающей среды (T1>T2). В этом случае        , и по разности температур можно установить, сколько времени прошло с момента совершения преступления.

Самый простой способ установить связь между          и – это полу чить соответствующее уравнение парной линейной регрессии. Зависимой переменной, естественно, выступает разность температур в градусах Цельсия, а независимой – время в минутах. Для оценивания параметров данного регрессионного уравнения лучшим способом будет метод наименьших квадратов. Такие уравнения легко получить по эмпирическим данным для разных тел и составить соответствующую удобную для пользователей таблицу либо делать это каждый раз непосредственно, сообразуясь с окружающими условиями.

На практике это возможно сделать, предприняв следующие шаги. Первый шаг – это заполнение рабочей таблицы из двух столбцов – столбца времени в минутах                и столбца с разностью температур                      , где            . Время здесь – независи мая переменная, а разность температур – зависимая. При этом мы точно знаем, что связь между переменными обратная. В простейшем случае мы получим линейное уравнение вида:                , где

– оценка разности температур, альфа и бета – оцененные методом наименьших квадратов параметры. Для точности в оценочное уравнение включен и случайный член .

Интерпретация оценочного уравнения тривиальна. Свободный член (пересечение прямой оси ординат в прямоугольной декартовой системе координат правой ориентации) – это максимальная разность температур между телом и окружающей средой в градусах Цельсия при t = 0. Параметр бета ( ) отвечает на вопрос, на сколько градусов Цельсия снижается разность температур при увеличении времени на одну минуту. Параметр бета получаем из формулы:

Covty

, где – ковариация между переменными модели, – дисперсия по независимой переменной. Параметр альфа получаем из уравнения: 70 , где и – соответствующие средние значения, при этом учитывая знаки, поскольку параметр бета у нас получится со знаком минус, а, следовательно, к среднему значению разности температур мы будем прибавлять произведение параметра бета на среднее время.

При малой начальной разности температур можно использовать простую линейную модель:               , получая довольно точные оценки. Однако, если эта разность велика или мы хотим повысить точность измерения, необходимо использовать не простую линейную модель, а модель линейную логарифмически. Для этого оценивание параметров регрессионного уравнения необходимо проводить с использованием логариф-мически-линейной модели. То есть в исходной рабочей таблице от обычных числовых значений в столбце разности температур нам необходимо будет перейти к логарифмам, а далее выполнять оценивание параметров уравнения тем же обычным методом наименьших квадратов. Двойную логарифмическую модель использовать нецелесообразно, по- скольку нам придется логарифмировать переменную времени и сопоставлять процентные соотношения времени и разности температур, что весьма неудобно.

Задача установления зависимости между разностью температур и временем может быть решена с помощью решения обыкновенного дифференциального уравнения с разделяющимися переменными. Дело в том, что скорость охлаждения тела, помещенного в среду dT с заданной температурой: dt пропорциональна разности между температурой этого тела и температурой окружающей среды, а поскольку мы рассматриваем вариант 71 > ?2 , то коэффициент пропорциональности будет отрицательным, и мы получим дифференциальное уравнение: ^=-k(T,-T2). При этом целесообразней сразу произвести замену пере-71 менных: Т1-Тг = y и записать нужное дифференциальное уравнение более dy , просто:           . Это обыкновенное дифференциальное уравнение первого порядка с разделяющимися переменными, записанное в явном виде.

Чтобы решить в общем виде дифферен- циальное уравнение:

необходимо dy i

— = —kat у               , вать левую dy dt

и

разделить

а далее

—ку , сначала переменные:

проинтегриро-

правую части уравнения:

$^ = "k$dt , получив в результате интегрирования: , где A – произвольная постоянная. Это и есть общее решение данного дифференциального уравнения, в результате которого мы получили семейство интегральных кривых, полностью описывающих исследуемый физический закон.

С учетом того, что у = ^ - т7, необходимо записать: у = Т-Т2 = Ae"kt и выразить температуру тела, щенного в окружающую среду с поме- задан-

ной температурой: T = T₂ + Ae"^kt . При t = 0 ясно, что T = T_± , откуда легко выразить произвольную постоянную:

4 = ^ -Г₂ и перейти к уравнению вида: T = T₂+(T₁- T₂)e"^kt .

Из уравнения" T = T2+(T1- T2)e-kt видно, что при t = 0 температура тела равна его начальной температуре T = TT , а при увеличении времени t > 0 его температура сначала начинает стремительно снижаться, потом процесс замедляется, но разность температур стремится к нулю, или, иными словами, температура тела стремится к температуре окружающей среды, согласно законам термодинамики.

Единственный незначительный недостаток уравнения T = T₂ + (7; -T₂)e"^kt по сравнению с простым линейным уравнением у = Ct — Pt + E – не наблюдается пересечения кривой функции с осью абсцисс (равно как и с осью ординат), хотя на самом деле это происходит в физической реальности, т.к. температуры полностью выравниваются, а не про- 71 сто асимптотически приближаются друг к другу. В этой части простое линейное уравнение точнее нелинейных, которые, в свою очередь, точнее аппроксимируют реальную зависимость в промежутке между начальной и конечной точками области определения функции, не включая лишь эти граничные точки области определения функции.

Необходимо отметить, что значение реальной функции, связывающей исследуемые переменные, в начале отсчета нам всегда точно известно – оно равно начальной разности т = тг-т2 , и значение функции в конце области определения функции нам также всегда точно известно – это T = TT - 7; = 0 . То есть по двум координатам: T(.O;ymQx) и T(.O, tmax) мы можем построить прямую: J j max      I , аппроксимирую щую искомую физическую связь в виде линейной обратной функции в области ее определения: Df = [O,tm(J. Оце-

.      у =    - ^^ t нивание по функции             ^mcu:

будет точнее, чем оценивание по функциям у = a — pt + £ и

Т = Г2 + (Тг -Т^е^, только в близких к крайним точках области определения исследуемой физической функции. Эту особенность и следует учитывать, используя для оценивания исследуемой функции, пары функций, в част-V = _Утаг t ности, функцию               t-miHC и функцию Т = Г2 + (^ -Т^е"^. Необходимо отметить, что ошибка оцени-у          — -'^^-^ f вания по функции             tmax будет равна разности определенных интегралов используемых функций в области их определения:

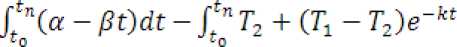
, то есть мы вычли из площади под грау = у — - mar фиком функции площадь под графиком функции т = Т2 +(7'1-7'2)e-fcfr.

Очевидно, что все построения были верны при условии, что температура окружающей среды не меняется за то время проведения исследования, а также все прочие важные условия, влияющие на температуру, являются равными. Например, труп находится в комнате с относительно постоянной температурой за исследуемый интервал времени. Аналогично и уличная температура определенное время остается постоянной, но если температура окружающей среды быстро меняется, то это осложняет исследова- ние и может привести к менее точным оценочным результатам, если не делать соответствующие поправки. Вместе с тем для производства расследования во многих делах чрезмерные тонкости физической теории уместно опустить, ограничившись применением простых правил и вычислений. Для наглядности можно провести простой эксперимент.

Необходимо разогреть в чайнике воду до кипения. В помещении, где находится чайник, измерить температуру и проследить с помощью специального, например, инфракрасного градусника за изменением температуры воды в чайнике по времени. В данном конкретном случае температура в помещении составляет 25 градусов Цельсия, а температуру кипящего чайника мы приняли за 100 градусов Цельсия. По итогам измерений составляем таблицу.

Таблица. Результаты измерений изменения температуры воды в чайнике

Table. Temperature changes of the water in the kettle

t	y	у-Т-Т2	In (у)
0	75	(100-25)	4,317
30	37	(62-25)	3,61
50	27	(52-25)	3,296
60	23	(48-25)	3,135
68	19	(44-25)	2,944
90	15	(40-25)	2,708
100	13	(38-25)	2,565
120	10	(35-25)	2,302
132	8	(33-25)	2,079
140	7,8	(32,8-25)	2,054

Интерпретация данной модели проста: если время увеличивается на 1 минуту, 72 то разность температур в среднем падает на 0,395°C .

Если использовать данное простое линейное уравнение и определить, до какой температуры вода в чайнике остынет, например, за 68 минут, то получим следующий результат: у = 54,76-0,395 -68= 27,9°С % 28°С .

На самом деле, вода остынет только до 44 градусов. Модель вида Т = Т₂+(Т_г- T₂)e"^kt даст гораздо более точный результат.

Рассмотрим, как работает модель: Т = Т₂ +(T₁-T₂)e-^kt . Нам известно, что при t = 0 температура воды в чайнике составляла 100 °C , то есть Т_г = 100°С. Температура в помещении составляла 25 °C , то есть Т₂ = 25°С. Спустя 30 минут от начала кипения чайника температура воды в нем равнялась 62°С. Нас интересует, через какое время температура воды в чайнике будет равна 40 °C. Из эмпирических данных, представленных в таблице, известно, что температура воды в чайнике будет равна 40 °C через 90 минут после начала отсчета, однако модель нам покажет,

Рисунок. Простая линейная модель зависимости разности температур от времени, построенная по данным из таблицы

Illustration. A simple linear model of the dependence of the temperature difference on

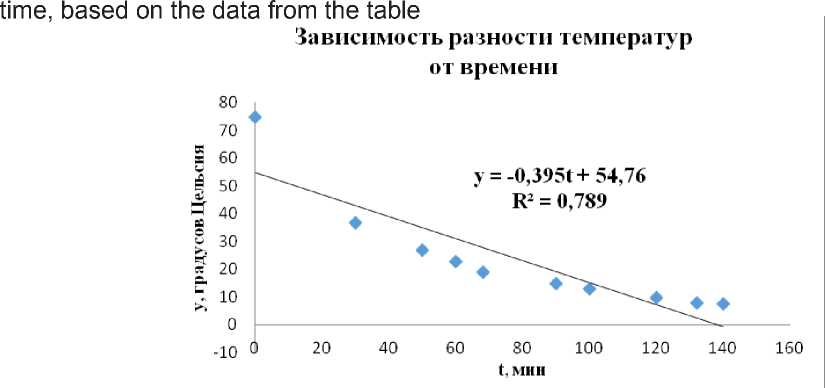
что 40 градусов вода должна будет достичь через 68 минут. На самом деле, согласно эмпирической таблице, через 68 минут температура воды в чайнике 73 составит не 40, а 44 градуса. Погрешность в расчетах невелика по сравнению с простой линейной моделью, тем не менее она присутствует.

Решение задачи. Первое уравнение: Т(0) = 25+Ле"^° = 100,   отку да Л = 100- 25 = 75°С. Далее запишем второе уравнение для времени: t = 30, то есть: Т(30) = 25 + Ле"к'30 = 62 (число 62 мы взяли из эмпирической таблицы, и оно у нас присутствует в условии задачи). Следовательно, Ле-^30 = 62 - 25 = 37. Поскольку A = 75, — к*30   ^7

имеем: "       75 и далее, поделив сте пени в левой и правой части уравнения на 30, запишем, учитывая, что в правой части уравнения выражение представле-

-к _ А37\ао но в первой степени:        V7 4/ .

r                         X./D/

Далее записываем уравнение к искомому ответу: Т = 25 + Ле"^ = 40,

40-25   15

откуда:   "          75     75 , но мы

—к f37\ao уже знаем, что               , и на ходим искомое время для остыва- ния воды в чайнике – до 40 °C:

1п(—) !    1п(—)

t = -7^ ^: - = "^ ' ³⁰ = ⁶⁸.³³ ^ ⁶⁸ _1ЛМОХ,_Т 1п(-) 30                            минут.

Как мы видим из эмпирической таблицы, за 68 минут вода в чайнике остынет только до 44 градусов, но не до 40. К 40 73 градусам температура воды охладится через 90 минут, поскольку скорость охлаждения воды имеет положительное ускорение вначале при большой разности температур, но затем происходит отрицательное ускорение, когда разность температур заметно уменьшается.

Рассмотрим также логарифмиче-ски-линейную модель. Логарифмиче-ски-линейная модель для приведенных эмпирических данных имеет вид:

. Интерпретируется она так: если t меняется на единицу измерения (в данном случае – это одна минута), то зависимая переменная меняется на величину: 100 ^%. Следовательно, для нашего примера имеем: 100 - 0,0155827 = 1,55827%. То есть если время увеличивается на одну минуту, то разность температур уменьшается примерно на 1,6%. В столбце разности температур максимальное значение (75) есть 100%, и от этого значения (75) с каждой минутой разность температур уменьшается на 1,6%. Через 10 минут разность упадет на 16%.

Сделаем предположение по этой модели для t = 68 минут. Запишем: ln(y) = p_o + Pit = 4,13237 - 0,0155827 ■ 68 = 3.0727.

Полученное значение лежит между числами 3,135 и 2,944 в эмпирической таблице, то есть 2,944 < 3,0727 < 3,135. При этом значению 2,944 в точности соответствует время – 68 минут.

При изучении разности температур мы сталкиваемся с важнейшим физическим понятием «теплоемкость». Удельная теплоемкость воды – с = 4200 Дж/(кг*град), а средняя теплоемкость тела человека – с = 3350 Дж/(кг*град). Для сравнения: теплоемкость подсолнечного масла 1700 Дж/(кг*град), железа – 460, золота – 130. Но при решении криминалистических задач, рассмотренных выше, мы не использовали значение теплоемкости и другие важные физические понятия, поскольку в каждом случае мы экспериментально 74 устанавливаем связь между температурой данного тела (не имеет значения, какого) и температурой окружающей его среды (не имеет значения, какой). Для решения более сложных физических задач необходимо проводить экспертное исследование (назначать экспертизу в соответствующем экспертном учреждении).

Обратим внимание, что использование уравнения T = T2 + (7^ - T2)e"kt, хотя оно и не регрессионное, тоже требует экспериментальных данных. То есть нам необходимо точно знать текущую температуру тела. Например, если у нас будет еще не остывший труп человека, то мы знаем его нормальную начальную температуру – 36,6 градусов Цельсия. Необходимо отметить, что температура человека на разных участках тела отличается. Например, нормальная температура лба – 33,4 °C , ладоней – 32,8 °C, подошв ног – 30,2 °C. Далее нам необходимо будет измерить текущую температуру трупа и температуру окружающей среды, но далее мы еще не сможем приступать к решению задачи с использованием уравнения: T = T2 + (7; - T2")e"kt, поскольку нам неизвестно время, за которое произошло остывание тела до текущей температуры. Необходимо будет подобрать объект с примерно такой же теплоемкостью, как и тело человека, провести соответствующий эксперимент при той же температуре окружающей среды и только потом провести оценку с помощью уравнения T = T2 +(Л — T2)e~kt или логарифмиче- 74 ски-линейной модели.

Мы доказали, что время совершения преступления может быть грубо приблизительно установлено по разности температур с помощью простого линейного регрессионного уравнения:

_v _ Утах

J Jmax . ^L_или V = Ct — 8t + E" ^rmax                            ^;

что довольно точно время совершения преступления может быть оценено с помощью логарифмически линейного уравнения: ln(y) = ^o + Pit или уравнения:

.