Устойчивость движения относительно части переменных непрерывно-дискретной системы
Автор: Лизина Елена Александровна
Журнал: Инженерные технологии и системы @vestnik-mrsu
Рубрика: Качественная теория дифференциальных уравнений
Статья в выпуске: 4, 2010 года.
Бесплатный доступ
Рассматривается вопрос о сведении задачи об устойчивости движения относительно части переменных непрерывно-дискретной системы к задаче об устойчивости движения по всем переменным для некоторой вспомогательной системы.
Короткий адрес: https://sciup.org/14719588
IDR: 14719588
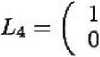
Список литературы Устойчивость движения относительно части переменных непрерывно-дискретной системы
- Воротников В. И. Устойчивость динамических систем по отношению к части переменных/В. И. Воротников. -М.: Наука, 1991. -288 с.
- Зубов В. И. Лекции по теории управления/В. И. Зубов. -М.: Наука, 1975. -495 с.
Статья научная
