Устойчивость гравитационно-связанного конденсата взаимодействующих бозонов

Современные данные астрофизических и космологических наблюдений показывают, что темная материя (ТМ) составляет большую часть иерелятивистского вещества, во Вселенной. Природа. ТМ и ее происхождение до сих пор остается загадкой, по в большинстве моделей ТМ состоит из нейтральных слабо взаимодействующих массивных частиц, которые не входят в Стандартную модель физики элементарных частиц [1,2].

“Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант № 20-52-05009) и Программы повышения конкурентоспособности Казанского (Приволжского) федерального университета.

• ¹    E-mail: niksamorodov@gmail.com

Одной из популярных моделей холодной ТМ являются легкие (псевдо)скалярные бозоны, образующие конденсат Бозе-Эйнштейна (БЭК) (см., например, [3] и ссылки в пей). Конденсированные бозоны имеют пулевой импульс и поэтому являются перелятивистскими независимо от их массы. Важным преимуществом этой модели ТМ является то, что профиль плотности галактического гало в пей не имеет центральной сингулярности. Опа естественным образом устраняется либо из-за. принципа, неопределенности Гейзенберга. [4], либо из-за. отталкивающего взаимодействия между конденсированными частицами [5], которое уравновешивает гравитацию.

Первая ситуация характерна, например, для сверхлегких бозонов с массами т ~ 10^-22 эВ или меньше, так что длина, волны де Бройля сравнима, с размером галактики, что обеспечивает волновое поведение частиц на. астрофизических масштабах. Гравитационное притяжение уравновешивается так называемым квантовым давлением, которое связано с кинетическим членом в гамильтониане, описывающем систему бозонов. Поэтому данное приближение называется кинетическим режимом. Альтернативным кинетическому режиму является приближение Томаса-Ферми, когда, квантовым давлением можно пренебречь, а. роль противовеса, гравитации играет отталкивающее взаимодействие.

Таким образом формируются компактные гравитационно-связанные БЭК, которые могут составлять как целое галактическое гало так и сравнительно небольшие «капли», разбросанные внутри галактики [6,7]. Такие объекты часто называют Бозе-звездами.

Компактные стационарные системы как релятивистских, так и иерелятивистских бозонов рассматривались иеодиократио [8-12], в том числе в контексте устойчивости и гравитационного коллапса. БЭК [13-16].

Стандартным подходом при исследовании устойчивости иерелятивистских звезд является приближение Каулинга [17], в котором игнорируются возмущения гравитационного потенциала. Использование приближения Каулинга. аргументируется тем, что основная масса, звезды концентрируется около ее центра, и больших возмущений гравитационного потенциала, возникнуть не может. Несомненным плюсом этого приближения является существенное упрощение уравнений, описывающих возмущения.

Устойчивость БЭК, описываемых стационарными решениями, полученными в приближении Томаса-Ферми рассматривалась в [18, 19]. В рамках приближения Каулинга. возмущения параметров БЭК носят осциллирующий характер как для радиальных, так и нерадиальных мод, что говорит об устойчивости системы.

В данной работе при исследовании на. устойчивость гравитационно-связанного конденсата, приближение Каулинга. не используется. Показано, что и в этом случае малые отклонения от равновесия не приводят к возникновению растущих мод как для радиальных так и нерадиальных возмущений.

• 1.    Профиль плотности конденсата

Нерелятивистский гравитационно-связанный БЭК, состоящий из взаимодействующих бозонов, описывается уравнениями Гросса-Питаевского-Пуассоиа [20]

гй ^W^) = (- ^^т ₊ mФ(r,t) + g|Ф(r,t)|²^ Ф(г, t),

(1.1)

(1.2)

V2Ф = 4тгСтп, где Ф(r,t) — волновая (классическая) функция конденсата, нормированная таким образом, что n(r,t) = |Ф(r,t)|2 есть плотность числа частиц, находящихся в гравитационном потенциале Ф(г, t), т — масса бозонов, ад — константа их взаимодействия, G — постоянная тяготения.

Систему уравнений (1.1) и (1.2) можно переписать в гидродинамическом представлении, разделяя амплитуду и фазу волновой функции конденсата (подстановка Маделунга [21]) Ф(г, t) = у/n(r, t) ег8(г,^/п. Тогда комплексное уравнение (1.1) преобразуется в уравнение непрерывности и уравнение Эйлера, дп „,  , д' + V(nv) = 0 ,

| v + ( v V) v = - - Vц, at           m

(1.3)

где скорость частиц конденсата определяется как v = VS/m, а ц химический потенциал коидеи-h V2Vn   _       _ _ _   _ _ сата. В приближении Томаса-Ферми слагаемым ---которое соответствует так называемому 2m "п квантовому давлению пренебрегают, что дает

ц = дп + m Ф .

(1.4)

Для установившегося равновесия химический потенциал является константой, и уравнения (1.3) удовлетворяются тождественно. Оставшиеся уравнения (1.2) и (1.4) дают решение для профиля плотности БЭК

sin (г/Д) "(г) = "° ДГ/RT'

(1.5)

где "о — плотность в центре БЭК, a R² = g/(4^Gm²) определяет характерный размер БЭК, так что его радиус равен ^R.

2. Устойчивость конденсата

Для исследования устойчивости БЭК линеаризуем уравнения (1.2), (1.3) и (1.4) относительно возмущений плотности конденсата 5"( r , t), его химического потенциала 5ц (г , t), скор ости 5 v ( r , t) = v ( r ,t) и гравитапиопиого потенциала. 5Ф( г , t):

д1" + V ("v) = 0,     |v + — V5ц = 0, at                   at m

V ² 5 Ф = 4 ^Gm5",      5ц = m5 Ф + д5п.

(2.1)

Удобно ввести вектор смещения, связанный со скоростью соотношением d s /dt = v. Тогда система. (2.1) сведется к единственному векторному уравнению

—- = 4^Gmn s + — graddiv(n s ). at ²              m

(2.2)

Нас интересуют решения уравнения (2.2), зависящие от времени как e^Mt, которые при действительных значениях ш описывают осцилляции s, а при комплексных значениях — экспоненциальный рост и убывание.

Перепишем уравнение (2.2) в безразмерных величинах:

п             r

"о’       ^ R’

t

^Т = Т,

(2.3)

где Т ² = (4^Gm"o) ¹ — характерное время свободного падения. Кроме того, представляя смещение в виде s = ж^-1(^) и (^)е^гПт, получим задачу на собственные значения

(1+0

u + grad div u = 0,

(2.4)

где параметр А = ш ² Т 2, а градиент и дивергенция теперь берутся относительно безразмерной координаты ф

Будем полагать, что компоненты вектора u не зависят от азимутального угла, тогда в уравнении (2.4) достаточно будет рассмотреть вектор вида.

U щ (ф9) е ₅ + и_е ( ф,9) е _е ,

(2.5)

где ф — безразмерная радиальная координата, определенная в (2.3). 9 — поляриый угол. a. e^ 11 e^ — соответствующие орты.

Решение уравнения (2.4) может быть представлено в виде разложений:

∞∞

".- («,9) = ^ «iGOP (cos 9 ) ,     uy ( «,9) = ^ p t (^)Р)¹ (cos 9 ) ,                 (2.6)

i=0                                     I =1

где P i (у) — полиномьi Лежандра, РДу) — присоединенные функции Лежандра 1-го порядка, а функции а₁ («) и Зр) ) удовлетворяют уравнениям:

(£ + 1) .0 + ()‘ = 0.

для радиальных возмущений, соответствующих I = 0, и

(А + 1) . i + (^)‘ + - ( + 1) (Р)‘ = 0.

при I = 1, 2,... Штрихом обозначена производная по переменной ф

(2.7)

(2.8)

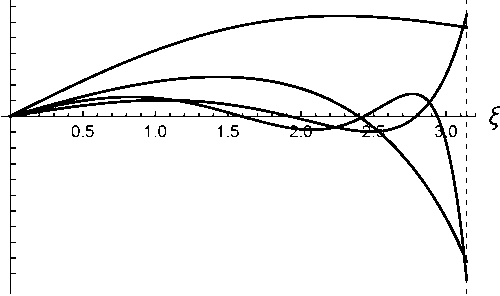
I = 0

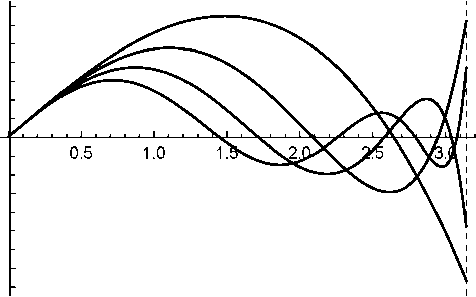
I = 1

А1 = 0.380, А2 = 1.618, Аз = 3.444, А4 = 5.849

А1 = 0.797, А2 = 2.302, Аз = 4.405, А4 = 7.089

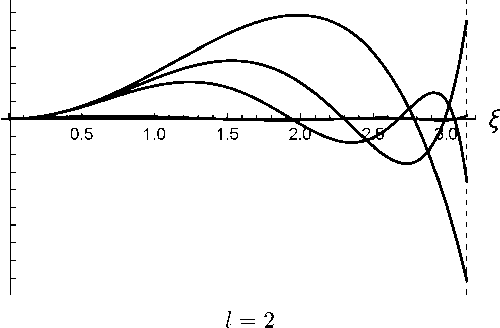
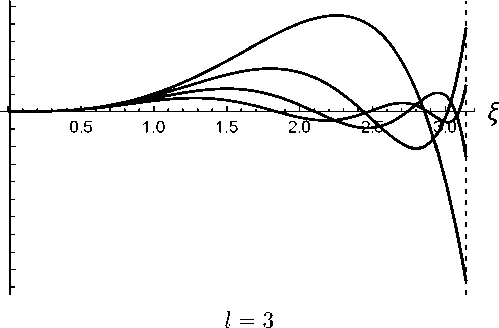
А1 = 1.196, А2 = 2.963, Аз = 5.334, А4 = 8.292

А1 = 1.579, А2 = 3.600, Аз = 6.234, А4 = 9.461

Рис. 1. Собственные функции возмущений плотности БЭК для сферических гармоник с I = 1, 2, 3. Для каждой гармоники представлены функции, соответствующие четырем первым собственным значениям, которые выписаны под рисунком. Штриховой линией обозначена граница БЭК £ = тг

Решения уравнений (2.7) и (2.8) для нескольких первых сферических гармоник получены численно; некоторые из которых них представлены на рис. 1. Граничные условия ставились, исходя из требования отсутствия смещения в центре и на границе БЭК. С помощью численных расчетов показано, что как для радиальных отклонений (Z = 0) так и низших иерадиальных отклонений (Z = 1, 2, 3), все собственные значения положительны. Это значит, что возмущения имеют характер пульсаций с частотами wik = V^ik(Т, где к нумерует моды осцилляций для Z-ой сферической гармоники.

На рис. 1 приведены собственные функции возмущений плотности БЭК бх = бп/по, которая, как легко убедится из (2.1), связана с вектором смещения соотношением бх = — divu.

Из-за. того, что градиент профиля плотности БЭК на. границе не равен пулю, па. отклонения плотности от равновесия накладывалось условие ограниченности. Более жесткое требование о равенстве бх нулю на границе приводит к большим значениям градиентов малых отклонений при £ ^ тт. Заметим, что аналогичное поведение имеет место при использовании приближения Каулин-га. Этот факт остался без внимания в работе [19] из-за. неверно определенной формы эффективного потенциала, в задаче на. собственные значения.

Заключение

В рамках приближения Томаса-Ферми рассматривалась задача, на. собственные значения для малых возмущений, возникающих в статическом конденсате взаимодействующих бозонов ТМ. Радиальные и нерадиальные отклонения от равновесия в БЭК исследовались без привлечения приближения Каулинга, то есть с учетом возмущений гравитационного потенциала. Для сферических гармоник Z = 0, 1, 2, 3 мы определили, что малые возмущения в БЭК осциллируют, а также вычислили несколько низших частот (в единицах, обратных времени свободного падения). Отсутствие растущих мод свидетельствует об устойчивости конденсата, относительно произвольных малых возмущений.