Устойчивость многослойных рекурсивных нейронных сетей

В статье рассмотрены многослойные нейронные сети с одинаковыми запаздываниями во взаимодействии между нейронами в сети. Такие модели имеют широкое применение в различных областях знаний.

В работе [1] изучалась нелинейная дискретная модель многослойных сетей. В этой работе даны достаточные условия глобальной устойчивости таких моделей. Наша задача другая – изучение локальной устойчивости и полное описание областей устойчивости в пространстве параметров.

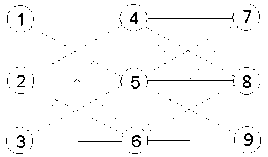
Рис. 1. Трехслойная нейронная сеть

Связи трехслойной сети с тремя нейронами в каждом слое изображены на рис. 1.

В результате линеаризации вокруг стационарного решения уравнений многослойной нейронной сети получается линейное матричное разностное уравнение xs = YIxs-1 + Bxs-k, s = 1,2- , где xs – вектор сигналов нейронов в момент s . Вектор xs – размерности np характеризует отклонения сигналов нейронов от стационарных, I - единичная np х np матрица, у - коэффициент затухания колебаний нейронов (0 < у < 1), B - матрица размера np х np , характеризующая взаимодействия между нейронами в сети, k – запаздывание во взаимодействии между нейронами, n – число нейронов в каждом слое, p – число слоев в сети.

Уравнение (1) принадлежит классу матричных разностных уравнений вида:

X s = AX s - 1 + BX s - k , s = 1,2 - , (2) которые обладают важным для нас свойством: матрицы A , B могут быть приведены к треугольному виду одним преобразованием. Поэтому мы имеем возможность применить метод конуса устойчивости [2] для анализа устойчивости этих уравнений.

Матрица B, например, трехслойной сети, состоящей из шести нейронов, имеет следующий вид:

f 0 0 a a 0 0 ) 0 0 a a 0 0 B = b b 0 0 a a b b 0 0 a a 0 0 b b 0 0 10 0 b b 0 0) где a – сила воздействия нейронов одного слоя на следующий слой, b – сила обратного воздействия.

Мы ставим задачу изучить область устойчивости системы (1) в пространстве параметров a , b при разных значениях γ , n , p и k .

Конус устойчивости для диагностирования устойчивости нейронных сетей

В работах [2, 3] введены конусы устойчивости для диагностирования устойчивости систем вида (2) с матрицами A , B , одновременно приводимыми к треугольному виду. Для решения поставленной задачи устойчивости многослойных нейронных сетей нам понадобится техника конусов устойчивости, которую мы здесь изложим.

Определение 1. Конусом устойчивости для уравнения вида (2) для данного k мы называем множество точек M = (u1,u2,u3)∈ R3 , такое, что u1 +iu2 = exp(ikω) - hexp(i(k -1)ω), u3 = h,(4)

где параметры h, ω связаны соотношениями sin kω   ππ

0≤h≤           ,- ≤ω≤ .(5)

sin(k - 1)ω kk

Теорема 1 [3]. Пусть A,B,S ∈ Rnp×np и S-1AS = AT,S-1BS = BT , где AT ,BT треугольные матрицы с диагональными элементами λj , µj соответственно (1 ≤ j ≤ np) . Построим точки Mj = (u1j,u2j,u3j)∈ R3 (1 ≤ j ≤ np) так, что u1j +iu2j =µj exp(-ik argλj), u3j = λj . (6)

Тогда уравнение (2) асимптотически устойчиво, если и только если все точки M_j лежат внутри конуса устойчивости (4), (6) для данного k . Если некоторая точка M _j лежит вне конуса устойчивости, то уравнение (2) неустойчиво.

Теорема 1 сводит задачу диагностирования устойчивости системы (2) порядка (np×np) к геометрической задаче в R3 : асимптотическая устойчивость системы равносильна условию, что все точки Mj(1 ≤ j ≤ np) лежат внутри конуса устойчивости (4), (6) для данного k .

Для применения теории конусов устойчивости необходимо знать собственные числа матри-

цы B . Введем следующие обозначения: ' 0 a 0 - 0 ) fl 1 1 - 1) b 0 a - 0 111⋯1 L= 0 b 0 - 0 ; V = 111 - 1 : : : 4 a •          •          •         • :     :     : ч 1 ( 0 0 0 b 0; (1 1 1 1 1J где матрица L размера (p× p) , матрица V размера (n×n) .

Заметим, что матрица L представляет собой матрицу сил запаздывающих взаимодействий нейронной сети линейной конфигурации. Собственные числа таких матриц и области устойчивости линейных нейронных сетей изучены в [4, 5].

Матрицу можно представить в виде произведения Кронекера следующим образом:

B = L ⊗ V .

Для произведения Кронекера справедлива следующая теорема.

Теорема 2 [6]. Пусть собственные значения квадратных матриц A и B равны α ₁,..., α _m и β ₁,..., β _m . Тогда собственные числа А ⊗ В равны α _i β _j .

Собственные числа матрицы L порядка p равны λ _j = 2 ab ⋅ cos

f]

( p + ¹ )

j = 1... p . Собст-

венные числа матрицы V порядка n равны µ1 =µ2 = ⋯ = 0 ; µn = n . Согласно теореме 2 для мат- рицы B порядка np собственные числа равны £11 = £12 =

= £ _pn - 1 = 0 ; £ j _n = 2 njab • cos

j = 1... p .

Диагностирование устойчивости двухслойной сети

Определение 2. Овалом устойчивости для уравнений вида (2) для запаздывания к > 1 и параметра y мы называем кривую M(to) = (u1(to),u2(to)), такую что u1 (to) + iu2 (to) = exp(ikto) -1у exp(i(к -1)to), где toe (-tol,to1), где to, - есть наименьший положительный корень уравнения

sin k to sin( к - 1) to

Овал устойчивости для данного запаздывания k и данного γ это сечение конуса устойчивости (см. Определение 1) плоскостью и3 = у. На основании Теоремы 1 и свойств матрицы B для диагностирования устойчивости уравнения (1) достаточно проверить две точки

M ( u 1 j , и ₂ j ) = u 1 j + iu ₂ j = ± 2 n4ab

• cos

(1 <  j <  2). Поэтому имеют место следующие теоре-

мы.

Теорема 3 . Пусть даны произвольные n , к e Z ₊ , к >  1. Пусть 0 <  у < 1. Построим в R ² овал устойчивости (см. Определение 2) для данных к , у . Построим точки M j = ( u 1 j , и ₂ j ) e R ² (1 <  j <  2)

так, что

u 1 j + iu ₂ j = ± 2 n4ab • cos

Если обе точки M j (1 <  j <  2) лежат внутри овала устойчивости, то система (1) асимптотиче-

ски устойчива. В противном случае система (1) неустойчива. Введем обозначение

q = 2 n • cos

Теорема 4. 1. Если у >  1, то система (1) неустойчива.

• 2.    Если

у <  1 и 0 <  ab <

(

V

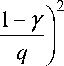
, то система (1) асимптотически устойчива при любом запаз-

дывании к . Если у <  1 и ab >

, то система (1) неустойчива при любом запаздывании k .

• 3.    Если у <  1 и ab <  0 и

| ab | <

f ^ (^2 ) ²

V q )

, то система (1) асимптотически устойчива при дан-

ном значении к . Если у <  1 и ab <  0 и

ab

f F ( у , к ) У

------I , то система неустойчива при данном

запаздывании к . Здесь F ( у , к ) =

sin to ( у ) cos( к - 1) « ( у )

где < у ( у ) есть наименьший неотрицательный ко-

cos k to рень уравнения у =---------.

cos( к - 1) to

Области устойчивости системы (1) отражены на рис. 2, 3.

Полученные результаты не противоречат известным результатам. Можно сделать вывод о динамике областей устойчивости в пространстве параметров. Область устойчивости стягивается в крест только с ростом числа нейронов в каждом слое. Увеличение числа слоев в нейронной сети с сохранением числа нейронов в каждом слое не стягивает область устойчивости в крест. При фиксированном количестве нейронов n имеется область в пространстве параметров, в которой гарантируется устойчивость независимо от запаздывания (delay-independent stability). Для сохранения устойчивости выгоднее увеличивать число слоев в многослойных сетях, чем наращивать число нейронов в каждом из слоев.

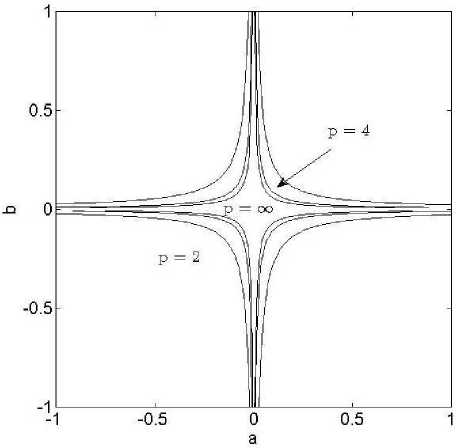
Рис. 2. Область устойчивости системы (1) в плоскости ( a, b ) при фиксированных у = 0,4, к = 3, n = 4 и переменном числе слоев p

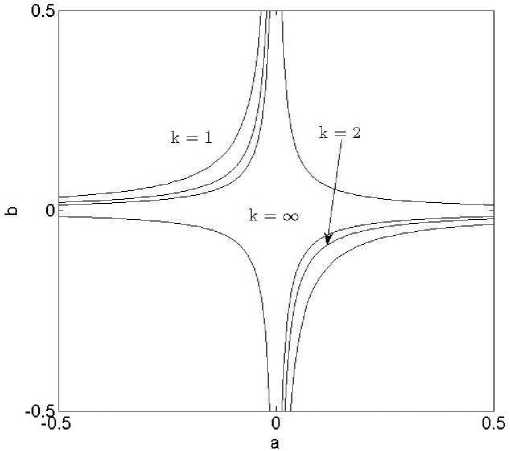
Рис. 3. Область устойчивости системы (1) в плоскости ( a, b ) при фиксированных у = 0,4, Р = 3, n = 5 и переменном запаздывании к