Устойчивость низкотемпературного плазменного шнура с учетом диссипации

Одной из простых равновесных конфигураций плазмы в магнитном поле является г -пинч, который часто используется для моделирования различных электродуговых разрядов [5]. Равновесие электрического столба (рис. 1) обеспечивается балансом дро     Во Э

^В_о) >                                  (1)

dr     4лг Эт где Во (г) ~ В^о — магнитное поле, ро — давление, индексом 0 отмечаем равновесные величины, которые могут зависеть только от г .

Характерной особенностью низкотемпературной плазмы, которая используется в различных технических устройствах, является зависимость коэффициентов теплопроводности, излучательной способности, проводимости от температуры и плотности [1], [4]-[6].

Дисперсионное уравнение

Будем основываться на МГД-уравнениях [3]:

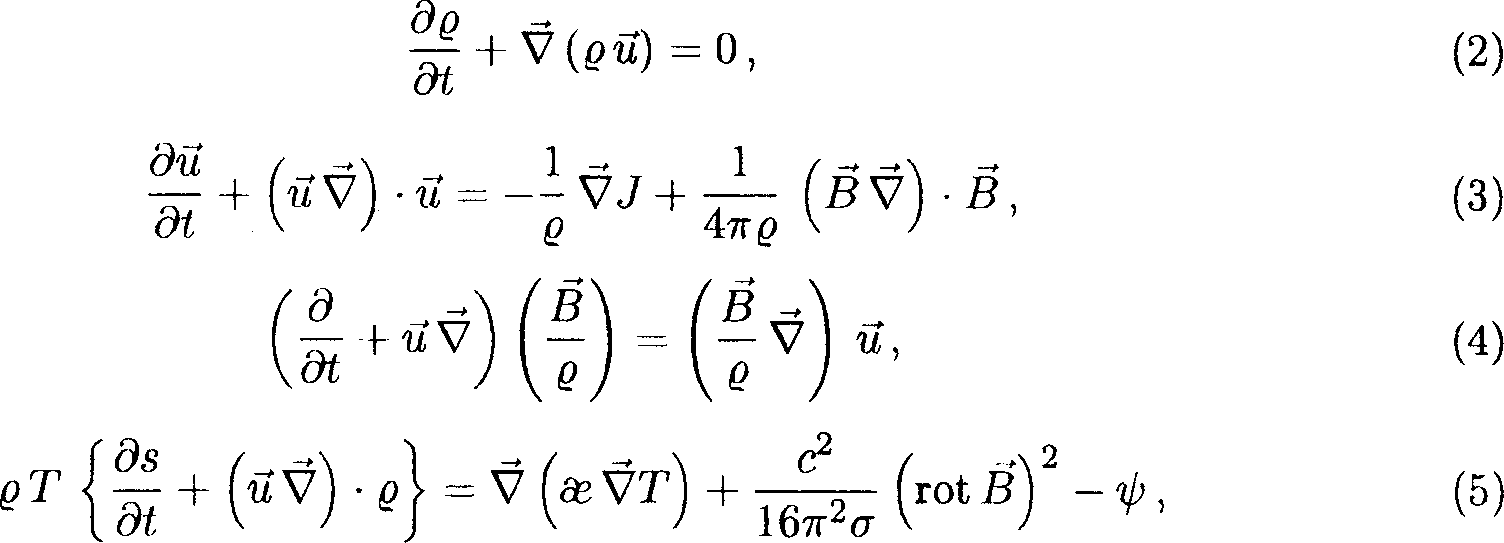
где и = {-и, г>, ш} — вектор скорости, q — плотность, J =- р + В² /8тг — полное давление, з — удельная энтропия, Т — температура, гв — коэффициент теплопроводности, сг — проводимость, -0 “ излучательная способность. В уравнении (4) пренебрегли диффузией магнитного поля. Ограничимся выражением для удельной внутренней энергии в = р/(7 — 1)5 (7 —- показатель адиабаты).

Вестник ВолГУ. Серия 1. Вып. 9. 2005 157

Линеаризуем исходную систему уравнений. С учетом однородности равновесного состояния вдоль z-координаты, для осесимметричных возмущений вида:

/(г, z, Z) — /(г) • exp^-iwt + ik₂z/

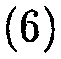
получаем для волн в частном случае df /dr = 0:

f оу2                                  | w5 — гПт ш4 + ш3 < —— (D^ + (In роУ) — к2 (Уд + c2) > + r lw2

. i^rk²M + Vj) - гПX к² - Ю^ (Di + (In р₀У)1 + ^ C²^ {

r

9У2

4 г (Q_T - Q_e) -^4k²D_T = 0,

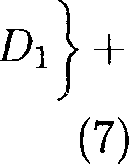
где cs — V^Po/Ро — адиабатическая скорость звука, 4 = <^/7, Уд = ^Bq/4tvoq — альвеновская скорость, штрих «: » — производная по г , L>i — — ш -- , величины dr \gor )

= (7-1) •

Г Ст Ро

[ро г ро ро J определяют диссипацию с учетом зависимости коэффициентов переноса от термодинамических параметров:

ХЭТ           \Эд/т        \Э1/е        \dg/T

В предельном случае однородной среды р'_о = В_о = 0 уравнение (7) приводит к uj²(w + гхк²) — к²с²(ш + i-xk²/^ = 0 , которое описывает звуковые волны с учетом затухания за счет теплопроводности (х ⁼ *o/cvРо) и затухание тепловой моды с декрементом

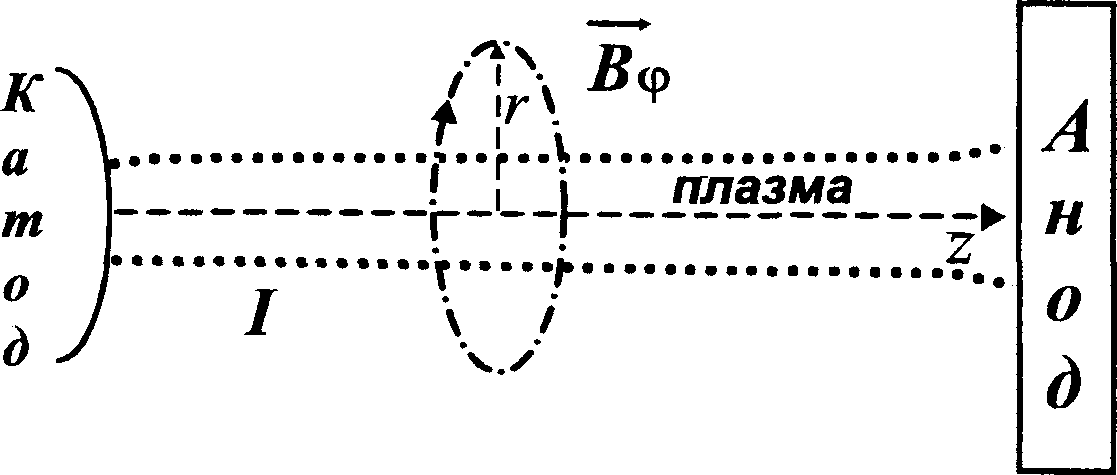
Рис. 1. Ток в плазме генерирует магнитное поле, которое обеспечивает равновесие плазменного столба

ш ₌ -ixk^ /7. В бездиссипативном случае уравнение (7) дает классический критерий устойчивости г-пинча относительно осесимметричных волн [2]:

rdpo

Podr

2 I 70 ’

(Н)

где 0 = 8лро/Вд • В случае /? > 27/З важную роль может играть змейковая неустойчивость для неосесимметричной моды [7].

Неустойчивость диссипативно-градиентных волн

Рассмотрим наиболее низкочастотную моду, описываемую уравнением (7). Для оценок запишем в линейном по От , П_е приближении выражение для частоты:

D₃ = - ---—.                (12)

(In So)' - 7D1

С учетом (1) и вводя параметр п(т) = d ln(p₀)/d 1п(^о), получим

п = _1 2 + ^ . 4п/(2 + /М ~ нр

• ³ п 2 + 07 47/(2 + 07) - Пр ’

где пр =        При п ~ 7 имеем условие D3 < 0, что обеспечивает затухание волны.

Podr

Однако в общем случае п Д 7 и в зависимости от значений параметров знак величины D3 может быть любым.

Если в От и Оу пренебречь производными, то при Оз > 0 имеем неустойчивое решение с инкрементом ш~гОзк^х-                          (14)

Тогда критерий появления неустойчивых решений принимает вид:

J 47 > (247/3)пр            / 47 < (2 + 7^)пр

( 4п < (2 + 0п) п_р ,               4п > (2 + 0п) п_р .

В столбе электрической дуги 0 > 1 . На рисунке 2 на плоскости параметров ж = п/п_р, у = 7/Пр показаны области устойчивости.

Для появления неустойчивых решений необходимы радиальная неоднородность равновесного состояния и учет диссипативных процессов. Причем, диссипативные факторы могут играть как стабилизирующую роль, так и дестабилизирующую. В более общем случае, чем (15), для неустойчивости необходимо:

J О₃ > О                / Оз <  0

Выполнение условий в существенной мере определяется зависимостью коэффициента теплопроводности сВ и излучательной способности -ф от плотности и температуры. Причем, величины дт, 6_д, Ат, Д_е могут быть и положительными и отрицательными [4], [5]. Влияние параметров 6т, 6_е, Ат, А_д в (16) возрастает с ростом длины волны вдоль z -координаты.

Вестник ВолГУ. Серия 1. Выл. 9. 2005

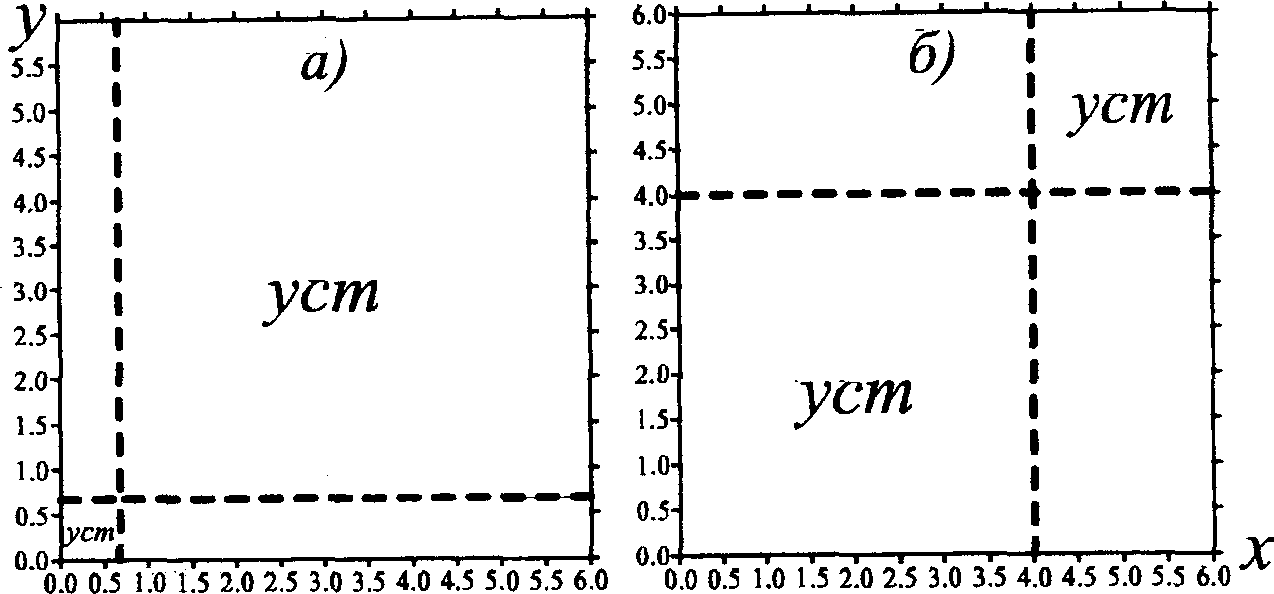
Рис. 2. Области устойчивости при п_рр = 1 (а), п_р/3 = 3.5 (6) в соответствии с условиями (15)