Устойчивость одного дифференциально-разностного уравнения с одним запаздыванием и с постоянными коэффициентами
Автор: Седова С.М.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Математика
Статья в выпуске: 2 (33), 2016 года.
Бесплатный доступ
Построены известные области асимптотической устойчивости и неустойчивости (в этом случае не полностью описана область) одного скалярного дифференциально-разностного уравнения с одним запаздыванием и с постоянными коэффициентами на плоскости параметров уравнения способом, развиваемым автором.
Дифференциальное уравнение с запаздывающим аргументом, области асимптотической устойчивости и неустойчивости
Короткий адрес: https://sciup.org/14730046
IDR: 14730046 | УДК: 519.929 | DOI: 10.17072/1993-0550-2016-2-50-55
Текст научной статьи Устойчивость одного дифференциально-разностного уравнения с одним запаздыванием и с постоянными коэффициентами
Предлагаемая работа продолжает исследования, опубликованные в [1] ,[2], [3].
В работе [1] для задачи Коши дифференциально-разностного уравнения с периодическими коэффициентами
x ( t ) -т^к ( t ) x ( t - к a ) = f ( t ), t > 0, (1)
к = 0
x ( £ ) = 0, £ < 0; x (0) = 1, где ak ( t ) - периодическая функция с периодом Tk = 1ка, lk e {1,2,..., m}, к = 0, m , т.е. периоды Tk рационально соизмеримы запаздываниям кю, f е Lloc [0, да ), был сформулирован критерий устойчивости, полученный в [4], [5], [6] , в редакции работы [6]. В [6] критерий имеет вид: пусть ак е L да [0, ma], к = 0, m , пусть C ( t , s ) - функция Коши уравнения (1) [7], [8], [9], [10], A m ( z ) - характеристическая
функция уравнения (1) [6], функция Коши C ( t , s ) имеет экспоненциальную оценку
|C(t,s)| < Ne-a(t-s),0 < s < t, при некоторых N > 0, a > 0 (задача I) тогда и только тогда, когда наименьший по модулю корень z0 уравнения Am (z) = 0 лежит вне единичного круга: |z0| > 1 (задача II). В этом критерии задача устойчивости (задача I) сведена к задаче о расположении нуля z0 целой функции Am (z) комплексного переменного z относительно единичной окружности (задача II) .
В работе [1] предложен способ решения задачи II, сформулированный в теоремах 2, 3, которые названы основными. В [1] характеристическая функция A m ( z ) обозначена через g ( z ) и подчеркнута зависимость от конечного числа параметров p = ( p 1 ,...,p h ), g ( z , p ). В основных теоремах критерий устойчивости приобретает такую формулировку, которая позволяет строить (или описывать) область асимптотической устойчивости S в пространстве параметров Op , а также область неустойчивости H = Op \ S .
В предлагаемой работе с помощью теоремы 2 (теоремы 2 и 3 [1]) осуществлено построение известных [10] областей S и H для уравнения с одним запаздыванием а, ю > 0, и постоянными коэффициентами a 0 , b 0 е R
;x ( t ) = a 0 x ( t ) + b 0 x ( t - а ), t > 0, (2) x ( % ) = 0, % < 0; x (0) = 1.
Области S и H находятся на плоскости Oab , здесь a = a0a,b = b0a - параметры уравнения (2).
Приведем необходимые для данной работы обозначения и результаты. В работе автора [6] методом производящих функций получена характеристическая функция (в обозначении работы [6]) А 2 ( z ) уравнения (2)
А 2 ( z ) = 1 - z2 e 2 a 0 ю - 2 ze a 0 ю sh ( b .a z ) = = 1 - z 2 e 2 a - 2 ze a sh ( bz ).
Нетрудно эту функцию представить в виде произведения двух функций
А 2 ( z ) = ( e a z + eb b )( - e a z + e - bz ) =
= g ( - z ) • g ( z ), где
g ( z ) = - e a z + e - bz . (3)
Очевидно, что g (0) = 1, и исследование расположения нулей функции А 2 ( z ) относительно единичной окружности | z | = 1 на комплексной плоскости C сводится к такому исследованию для функции g ( z ) .
Как видно из выражения (3), функция g ( z ) зависит от двух параметров a , b , т.е. g ( z , a , b ), a , b е R . Функция g ( z ) - целая функция в комплексной плоскости C .
Критерий устойчивости для задачи Коши уравнения (2) имеет следующую формулировку.
Теорема 1. Пусть z 0 - наименьший по модулю нуль функции g ( z ). Если | z 0| > 1, то уравнение (2) асимптотически устойчиво, если | z 01 < 1, то уравнение (2) неустойчиво, если | z 0| = 1, то уравнение (2) устойчиво (неасимптотически).
Сформулируем теоремы 2, 3 из [1].
Пусть рассматривается уравнение (1), w = g ( z ) - характеристическая функция уравнения (1), целая функция на плоскости C .
Известно, что g (0) = 1. Пусть U - единичный круг на плоскости C : | z | < 1. D = g(U ) - образ единичного круга U при отображении g ( z ) , 5 D = g ( 5 U ) - линия, ограничивающая D . D = D J d D . Отметим свойства множества D :
-
1. d D - замкнутая кривая. Кривая д D может иметь точки самопересечения (т.е. может не являться жордановой кривой [12]).
-
2. D - область (открытое связное множество в C ) [12].
-
3. Область D симметрична относительно вещественной оси Ou , т.е. если w е D , то и w е D .
Рассмотрим образ д D единичной окружности z = el ,p , ф е [ 0,2 п ] , при отображении g ( z ) и функцию w = g ( e i " ) , р е [ 0,2 я ] , задающую д D . Пусть в функции w = g ( e ' " ) выделены вещественная u ( ϕ ) и мнимая v ( ϕ )
части g (ei’ ) = u (ф) + iv (ф);
выражение g ( z ) зависит от конечного числа параметров, т.е. g ( z , p ), p = ( p 1 ,..., ph ), для уравнения (2) g ( z , a , b ) . Пусть известны все или часть нулей функции v ( ϕ ) , т.е. " k е [ 0,2 n ] , при которых v(" k ) = 0, k = 1, l .
Теорема 2 (теоремы 2, 3 в [1])
-
1) Пусть в точке P ( p ) пространства параметров Op уравнения (1) ( P ( a , b ) плоскости Oab параметров a , b уравнения (2)) при некотором "k е [ 0,2 ^ ] имеем: v("k ) = 0 и u ("k ) < 0, тогда точка P принадлежит области неустойчивости H уравнения (1).
-
2) Пусть в точке P ( p ) е Op при всех Ф е [ 0,2 п ] , для которых v(ф ) = 0, имеет место неравенство и(ф ) > 0, тогда точка P принадлежит области S асимптотической устойчивости уравнения (1).
Замечание 1. Система v (Ф, p) = 0
и ( ф , p ) > 0,
Ф е [ 0,2 п ]
задает область асимптотической устойчивости S уравнения (1) в пространстве Op парамет- ров p уравнения (1). А именно, если уравнение v(ф, p) = 0 имеет l решений фk, k = 1, l, l > 1, на промежутке [0,2п], то для каждого корня фk находим область Sk параметров p, при которых и (фk, p) > 0. Область S находим пересечением областей Sk, S = Q Sk . Далее, k для каждого корня фk находим область Hk параметров p, при которых и (фk, p) < 0. Область H находим объединением областей Hk, H = U Hk . Учитывая замечание 1, полу-k чаем, что система fv (ф, a, b) = 0
-
7 фе 0,2п ,(4)
[и(ф,a,b)>0
имеющая место для всех найденных ϕ одновременно, задает область асимптотической устойчивости S уравнения (2) на плоскости Oab параметров a , b уравнения (2) .
Замечание 2. Уравнения и (ф, a, b) = 0, v (ф, a, b) = 0
определяют на плоскости Oab точки ( a , b ) , в которых уравнение g ( z , a , b ) = 0 имеет корень z 0 на единичной окружности, т.е. z 0 ед U , однако, в этих точках ( a , b ) также могут быть корни z 0 , принадлежащие единичному кругу U .
Теорема 3. В системе (4) достаточно считать, что ф с [ 0, п ] .
Замечание 3. Теорема 3 имеет место в силу свойства 3 области D .
-
§ 1. Область асимптотической устойчивости
Рассмотрим функцию (3) g ( z ) = - e a z + e - bz .
Для функции w = g (е‘ф) = Re g (е‘ф) + i Im g (е‘ф) = = и (ф) + iv (ф)
функции u(ϕ),v(ϕ) имеют вид и (ф) = — ea cos ф + e-b cosф • cos (b sin ф), v(ф) = — ea sin ф — e-b cosф • sin (b sin ф), (5)
ф с [ 0, п ] .
Рассмотрим сначала концы отрезка [0, п] . Точки ф = 0,ф = п - нули функции v (ф). Уравнение и (0) = - ea + e -b = 0 приводит к уравнению b = -a , (6)
которое задает прямую на плоскости Oab , участвующую в построении областей S и H .
Неравенство и (0) < 0, или b > - a, задает область неустойчивости H 1, H 1 с H . Неравенство и(0) > 0, или b < - a , (7)
задает область S 1 , S с S 1 .
Отметим частный случай уравнения (2) при b 0 = 0, функция g ( z ) имеет вид
g ( z ) = e a z + 1 .
Нуль этой функции z 0 = e- a £ U при a < 0 , т.е. в этом случае уравнение (2) асимптотически устойчиво. При a > 0 выполнено условие: z 0 = e - a е U , уравнение (2) неустойчиво.
Уравнение и ( п ) = e a + e b = 0 не имеет решений, поэтому не возникает линии, участвующей в построении областей S и H .
Рассмотрим случай фс( 0, п). Если предположить существование решения уравнения v (ф) = 0 на интервале (0, п), то получим e-bcosф • sin (bsinф)
e a =-- (------ . (8)
sin ϕ
Отметим, что случай b = 0 в (8) исключается. Получим сначала необходимые для построения областей S и H линии из системы и (ф) = 0
v ( ф ) = 0 ’
ф с ( 0, п ) .
В случае b ^ 0 система (9) имеет вид e b cosф • sin (b sin ф + ф) и (ф) =---------—---------- sinϕ a_ e-bcosф • sin (b sin ф) sinϕ
= 0
, (10)
ф с ( 0, п ) .
Из 1-го уравнения в (10) имеем sin (b sin ф + ф) = 0 , или b sin ф + ф _ nj, j e Z . (11)
При j _ 0 имеем b _ —ф-; из 2-го уравне-sinϕ ния в (10), или из (8), имеем ea _ e-bcosф , или a = -b cos ф.
В итоге получаем линию на плоскости Oab , заданную параметрически:
a _ - b cos ф
' b _- у , фе(0,n), sin ф или
_ фcosф a sin Ф Го )
) ,ф е( 0, n ) , (12)
b =--Л-sin ф которая так же, как и прямая (6), участвует в построении областей S и H .
Эта линия расположена в нижней полуплоскости; она "выходит" из точки (1; -1)e Oab, находящейся на прямой b = -a (самой линии эта точка не принадлежит), при π ф ^ +0; пересекает ось Ob при ф _ — в точ-
I П )
ке I 0;-у I и устремляется снизу к асимптоте b _ a при ф ^ n - 0.
При j _ 2 k , k _± 1, ± 2,.
..
, в (11) имеем
b sin ф + ф _ 2пк , (13)
или b sin ф = -ф + 2пк ; из 2-го уравнения в (10) получаем уравнение ea _ e-bcosф , или a = -b cos ф. (14)
В итоге из (13), (14) получаем совокупность линий, заданных параметрически:
a _ - b cos ф
-
< b _ - ф + 2пк ,ф е ( 0, п ) , sin ф
или
' а _(ф - П ) cos ф sin ф b _-ф + 2пк sin ф к _ ±1,±2,... .
, ф е ( 0, п ) , (15)
Опишем линии (15), отдельно рассматривая случаи к > 0 и к < 0 , при этом номер обозначим снова через к , здесь к _ 1,2,...
(ф - 2пк) cos ф sinϕ b _-ф + 2пк sinϕ
(ф + 2пк) cos ф sinϕ b _-ф - 2пк sinϕ
, ф е ( 0, п ) ,
ф е ( 0, п ) ,
Линии (16), (17) "устроены" просто: каждая похожа на ветку гиперболы. Опишем их единым образом, используя знак: /, т.е. свойство для (16)/свойство для (17). Линии расположены в верхней/нижней полуплоскости; ветви линий направлены вверх/вниз; линии "отходят" от асимптоты b _ - a (сверху) / b = - a (снизу) при ф ^ +0; к-ая линия про ходит через точку I 0; — + 2пк I /
) П
- 2пк I оси Ob при ф _ —; затем ли
0;-1
нии устремляются к асимптоте b _ a (сверху) / b = a (снизу) при ф ^ п - 0. С ростом ф от
0 до п точка ( a ; b ) движется по линии слева направо/справа налево. Линии (16)/(17) не пересекаются, что нетрудно показать от противного; с ростом номера k располагаются одна над/под другой. Линии не имеют точек самопересечения, что тоже нетрудно показать, поэтому их форма напоминает гиперболу. 1-ая линия в (17) расположена ниже линии (12) . На рис. показаны линии (16)/(17) при к _ 1.
При j _ 2к -1, к e Z, в (11) имеем b sin ф + ф _ (2пк - 1)п , или b sin ф _ -ф + (2пк - 1)п ; из 2-го уравнения в (10) получаем равенство ea _ -e-bcos ф которое не имеет место ни при каких a,b,фе R, т.е. в этом случае не возникает линий, участвующих в построении областей S и H.
Перейдем к построению областей S и H . Рассмотрим систему
и (ср ) > 0
v ( р ) = 0
р е ( 0, п ) ,
описывающую область (или области), которая участвует в построении области S . Система (18) при b ^ 0 имеет вид
e b cosр • sin ( b sin р + р )
sinϕ a_ e-bcosр • sin (b sin р) , sinϕ
или
sin ( b sin р + р ) > 0
a = - b cos р + In
sin ( b sin р ) '
sin р ;
S 1 Q S 2 , поэтому область S 1 Q S 2 не может быть уменьшена. По этой же причине (линии (15) не содержатся в области S 1 Q S 2 ) был рассмотрен один случай системы (19).
Таким образом, S = S 1 Q S 2 . Область асимптотической устойчивости уравнения (2) построена (см. рис., также [11], с. 126).
Про область неустойчивости H пока скажем только, что Oab \ ( S 1 Q S 2 ) с H . Неизвестна принадлежность H линий, ограничивающих область S = S 1 Q S 2 . Таким образом, доказана теорема:
Теорема. Область асимптотической устойчивости S уравнения (2) имеет вид: s = s 1 Q s 2 .
Уделим внимание одному случаю в (19) (далее поясняется, почему следует рассмотреть только этот случай)
0 < b sin р + р < п , или
- р < b sin р < п - р . (20)
Рассмотрим сначала случай 1) b < 0 в (20), или b sin р < 0, с учетом (20)
- р < b sin р < 0, р е ( 0, п ) , отсюда и из (19)
—— < b < 0 sin ϕ
a = - b cos р + ln
sin ( b sin р ) '
sin р ;
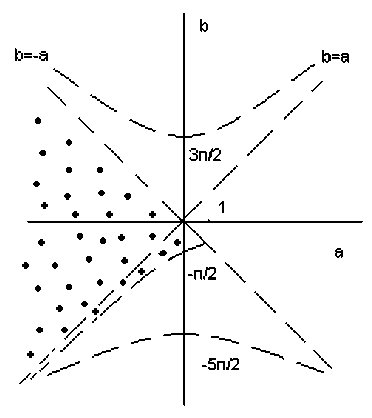
Область асимптотической устойчивости S (обозначена точками) между прямой b = -а и линией a = -bcosр,b = -р/sinр,ре(0,п)
р ^ ( 0, п ) .
Система (21) описывает область в нижней полуплоскости над линией (12) .
В случае 2) b > 0 в (20), или b sin р > 0, с учетом (20)
0 < b sin р < п - р , р е ( 0, п ) , уравнение (8) не имеет решений, что означает, что систему (18), или (19), рассматривать не нужно.
Обозначим через S 2 область над линией (12). Имеем, что S с S 1 Q S 2 .
Покажем, что S = S 1 Q S 2 . Так как ни одна из линий (15) не содержится в области
Список литературы Устойчивость одного дифференциально-разностного уравнения с одним запаздыванием и с постоянными коэффициентами
- Седова С.М. О критерии устойчивости дифференциально-разностных уравнений//Вестник Пермского университета. Математика. Механика. Информатика. 2011. Вып. 3(7). С. 6-11.
- Седова С.М. Устойчивость одного дифференциально-разностного уравнения с периодическим кусочно-постоянным коэффициентом//Вестник Пермского университета. Математика. Механика. Информатика. 2012. Вып. 2(10). С. 5-14.
- Седова С.М. Устойчивость одного дифференциально-разностного уравнения с постоянным коэффициентом//Вестник Пермского университета. Математика. Механика. Информатика. 2015. Вып. 1(28). С. 11-16.
- Рехлицкий З.И. Об устойчивости решений дифференциально-разностных уравнений с периодическими коэффициентами//Изв. АН СССР. 1966. Т. 30, вып. 5. С. 971-974.
- Малыгина В.В. Об устойчивости функционально-дифференциальных уравнений: дис.. канд. физ.-мат. наук. Пермь, 1983. 101 с.
- Седова С.М. Устойчивость линейных дифференциально-разностных уравнений с периодическими коэффициентами: дис.. канд. физ.-мат. наук. Пермь, 2000. 130 с.
- Азбелев К.В., Максимов В.П., Рахматуллина Л.Ф. Элементы современной теории функционально-дифференциальных уравнений. Методы и приложения. М.: Институт компьютерных исследований, 2002. 384 с.
- Азбелев И.В., Березанский Л.М., Симонов П.M. и др. Устойчивость линейных систем с последействием. I//Дифференциальные уравнения. 1987. Т. 23, № 5. С. 745-754.
- Азбелев И.В., Симонов П.M. Устойчивость уравнений с запаздывающим аргументом//Известия вузов. Математика. 1997. № 6. С. 3-16.
- Азбелев И.В., Симонов П.M. Устойчивость решений уравнений с обыкновенными производными. Пермь: изд-во ПТУ, 2001. 230 с.
- Эльсгольц Л.Э., Норкин С.Б. Введение в теорию дифференциальных уравнений с отклоняющимся аргументом. М.: Наука, 1971.296 с.
- Маркушевич А.И., Маркушевич Л.А. Введение в теорию аналитических функций. М.: Просвещение, 1977. 320 с.


