Устойчивость одного дифференциально-разностного уравнения с постоянным коэффициентом

Предлагаемая работа продолжает исследования, опубликованные в работе [1] .

В [1] для задачи Коши дифференциально-разностного уравнения с периодическими коэффициентами

Х ( t ) -^a_k ( t ) x ( t - k m ) = f ( t ) , t >  0, (1) k = 0

x (£) = 0, £ < 0; x (0) = 1, где ak (t) - периодическая функция с периодом Tk = lkm, lk e {1,2,..., m}, k = 0,m, т.е. периоды Tk рационально соизмеримы запаздываниям km, f e Lloc [0, да), был сформулирован критерий устойчивости, полученный в [2], [3], [4], в редакции работы [4]. В [4] критерий имеет вид: пусть ak e Lm[0,mm], k = 0,m, пусть C(t, s) — функция Коши уравнения (1) [5], [6], [7], Д mm (z) - характеристическая функция уравнения (1)  [4], функция Коши C(t, s) имеет экспоненциальную оценку

| C(t, s)| < N exp(—a(t - s)), t > s > 0, при некоторых N > 0, a > 0 (задача I) тогда и только тогда, когда наименьший по модулю корень z0 уравнения Дmm (z) = 0 лежит вне единичного круга: |z01 > 1 (задача II). В этом критерии задача устойчивости (задача I) сведена к задаче о расположении нуля z0 целой функции Дm (z) комплексного переменного z относительно единичной окружности (задача II) .

В работе [1] предложен способ решения задачи II, сформулированный в теоремах 2, 3, которые названы основными. В [1] характеристическая функция Д mm ( z ) обозначена через g ( z ) и подчеркнута зависимость от конечного числа параметров p = { P l , p 2 ,-, p h }, g ( z , p ) . в основных теоремах критерий устойчивости приобретает такую формулировку, которая позволяет строить (или описывать) область асимптотической устойчивости S в пространстве параметров Op , а также область неустойчивости H = Op \ S .

В предлагаемой работе с помощью теоремы 2 (теоремы 2 и 3 [1]) осуществлено построение известных [2] областей S и H для уравнения с одним запаздыванием о ,

ы >  0 , и постоянным коэффициентом a , a g R ,

X(t ) = ax ( t - ы ), t >  0 ,            (2)

x ( £ ) = 0, £ <  0; x (0) = 1 .

Области S и H находятся на прямой 0( а ы} , здесь а а - параметр: область асимптотической устойчивости S имеет вид

п

S = { а ы : a ыG ( -— ,0)} ,    (3)

область неустойчивости имеет вид

H = { а ы : а ы g ( -м ; -

п ) U (0, +» )} . (4)

Приведем необходимые для данной работы обозначения и результаты. В работе [4] получена характеристическая функция g ( z ) уравнения (2)

g ( z ) = 1 - ze- . (5)

Как видно из выражения (5), функция g ( z ) зависит от одного параметра аы , который обозначим b , b = аы , т.е. g ( z , b ) , b g R .

Функция g ( z ) - целая функция в комплексной плоскости C .

Критерий устойчивости для задачи Коши уравнения (2) имеет следующую формулировку.

Теорема 1. Пусть z0 - наименьший по модулю нуль функции g(z), если z0 > 1, то уравнение (2) асимптотически устойчиво, если |z01 < 1, то уравнение (2) неустойчиво, если | z01 = 1, то уравнение (2) устойчиво (неасимптотически).

Сформулируем теоремы 2, 3 из [1].

Пусть рассматривается уравнение (1), w = g (z) - характеристическая функция уравнения (1), целая функция на плоскости C . Известно, что g(0) = 1. Пусть U - единичный круг на плоскости C : |z| < 1. D = g(U) - образ единичного круга U при отображении g (z), дD = g (dU) - линия, ограничивающая D. D = D J дD. Отметим свойства множества D :

• 1.    д D - замкнутая кривая. Кривая dD может иметь точки самопересечения (т.е. может не являться жордановой кривой [8]).

• 2.    D - область (открытое связное множество в C ) [8].

• 3.    Область D симметрична относительно вещественной оси Ou , т.е. если w g D , то и w g D .

Рассмотрим образ dD единичной окружности z = e^{li p} , p g [0,2 п ] , при отображении g ( z ) и функцию w = g ( e i ^p ), p g [0,2 п ] , задающую dD . Пусть в функции w = g ( e i ^p ) выделены вещественная u ( p ) и мнимая v ( p ) части g ( e‘ ^p ) = u( p ) + Iv ( p ); выражение g ( z ) зависит от конечного числа параметров, т.е. g ( z , p ) , p = ( P 1 ,..., P h ) , для уравнения (2) g ( z , b ) . Пусть известны все или часть нулей функции v ( p ) , т.е. p k g [0,2 п ], при которых v ( p k ) = 0 , k = 1 ,n .

Теорема 2 (теоремы 2, 3 в [1]).

• 1)    Пусть в точке P ( p ) пространства параметров Op уравнения (1) ( P ( b ) прямой 0 b параметра b уравнения (2)) при некотором p g [0,2 п ] имеем: v ( p ) = 0 и

• u (p) < 0, тогда точка P принадлежит об-
• ласти неустойчивости H уравнения (1).

• 2)    Пусть в точке P ( p ) g Op при всех

p g [0,2п], для которых v(p) = 0, имеет ме сто неравенство u(p) > 0, тогда точка P принадлежит области S асимптотической устойчивости уравнения (1).

Замечание 1 . Система

' v ⁽ P , p ) = ⁰,

. u ( p , p ) >  0,

p g [0,2 п ] ,

задает область асимптотической устойчивости

S уравнения (1) в пространстве Op парамет- ров p уравнения (1). А именно, если уравне ние v (p, p) = 0 имеет l решений  pk, k = 1,2,...,l, l > 1, на промежутке [0,2п], то для каждого корня ~к находим область Sk параметров p, при которых u (pk,p) > 0 .

Область S находим пересечением областей Sk, S = Q Sk . Далее, для каждого корня pk k находим область H k параметров p , при которых u (pk,p) < 0 . Область H находим объединением областей Hk, H = J Нк .

k

Учитывая замечание 1 , получаем, что система

V ( ф , b ) = 0,

^, ф e [0,2 п ] ,   (6)

u (ф, b) > 0, имеющая место для всех найденных ф одновременно, задает область асимптотической устойчивости S уравнения (2) на прямой 0b параметра b уравнения (2)

Замечание 2. Уравнения и ( ф , b) = 0 , v ( ф , b ) = 0 определяют на прямой 0 b точки, в которых уравнение g ( z , b ) = 0 имеет корень z ₀ на единичной окружности, т.е. z ₀ e д U .

• § 1. Область неустойчивости

Построим область неустойчивости H (4) для уравнения (2)

H = {b : b e (-®-П)J (0,+®)},(7)

используя теорему 2.

Функция g ( z ) имеет вид

• g(z) = 1 - zebz, z e C.(8)

Условие g (0) = 1 выполнено. Функции

и ( ф ) = Re g ( e^ ), v ( ф ) = Im g ( e^{i ф} ) , ф e [0,2 п ] , имеют вид

и(ф) = 1 - ebcosф • cos(ф + bsinф),(9)

v ( ф ) = - e^{b cos ф} • sin( ф + b sin ф ) .

Согласно теореме 2, для построения области неустойчивости уравнения (2) следует найти такие значения параметра b уравнения (2), при которых корни ф уравнения v(ф) = 0 дают отрицательный знак числу и (~). Уравнение v (ф) = 0 эквивалентно уравнению sin(ф + bsin ср) = 0. (10) Таким образом, ограничения на параметр b получаем, находя такие ф e [0,2п], при ко- торых имеет место система sin(ф + b sin (р) = 0

1 — e^{b cos ф} • cos( ф + b sin (p ) <  0

.

Промежуток [0,2 п ] для ф можно уменьшить согласно следующей теореме.

Теорема 3. В системе (11) достаточно считать, что ф e [0, п ] .

Доказательство. Пусть рассмотрен случай ф e [0, п ] , где sin ф >  0 . По системе

sin в = 0

- е ^а • cos в <  0

ф e [0, п ] ,

где в = ф + b sin ф, а = b еosф, которая яв- ляется системой (11) с уменьшенным промежутком для (р, построена область H с 0b.

Тогда для случая sin ф <  0, т.е. для

(р e [ п ,2 п ] , сделаем замену переменной 2 п - ф = t . Здесь имеет место sin( - ф ) >  0 , - 2 п <-ф <- п , или sin(2 n - ф ) >  0 , 0 <  2 п - ф <  п , или sint >  0 , t e [0, п ] . Система (11) в результате подстановки ф = 2 п - 1 не изменяется, т.е. если в (12) считать (р e [ п ,2 п ] , то будет построена та же область H . В итоге можно считать, что ф e [0, п ] в системе (11), или рассматривать систему (12) для построения области H . ■

Замечание 3. Теорема 3 имеет место в силу свойства 3 области D .

Начнем рассматривать систему (11) при крайних значениях ф : ф = 0 , ф = п . ф = 0 уравнению в (11) удовлетворяет, при ф = 0

неравенство в (11) принимает вид 1 - eb < 0, или b > 0 , (13) что является первым найденным ограничением на b. Неравенство (13) задает область H на прямой 0b .

(р = я уравнению в (11) удовлетворяет, при ф = п неравенство в (11) имеет вид 1 + е - ^b <  0 и не выполняется ни при каких b: b e R . ф = п не является решением системы (11), дополнительных ограничений к неравенству (13) не появилось.

Рассмотрим корни уравнения (10) на интервале (0, п). Уравнение (10) эквивалентно совокупности уравнений ф + b sin ср = П, j e Z , которую следует рассматривать лишь при четных j, j = 2k, k e Z, ф + b sin (p = 2П,        (14)

что обосновывается следующим образом : при нечетных j неравенство в (11) имеет вид 1  . b cos ф .

1 + е    < 0, которое не выполнено ни при каких b, ф e R .

Рассмотрим случай k = 0 в (14), т.е. уравнение ф + bsin(р = 0, ф e (0,п) ,     (15)

или b =--—. График функции у =--, sin у                         sin ф ф е (0, п) , приведен на рис. 1.

Пусть некоторое ф е (0, п) - решение уравнения (15). Неравенство в (11) принимает вид 1 - еЬсооф < 0, или bcos ф > 0, что эквива- лентно совокупности систем

J b > 0 J b < 0 [cos ф > 0,  [cos ф < 0, или b > о

{фе (0,П),

J ^b<  ⁰

1    (п V(17)

фе (—,п)7

Если ф - решение уравнения (15) на промежутке (0,П), то соответствующее b =--— < 0 (см. график функции) и систе- sin ф ма (16) несовместна с уравнением (15). Не появилось нового ограничения на b .

Рассмотрим уравнение (15) и систему

• (17) . Уравнение (15) перепишем в виде

b = -^ф ,         (18)

sm ф откуда получим ограничение на b . Чтобы уравнение (15) (или (18)) имело решение ф п .

на промежутке (—, п) при b < 0 (это условия в (17)), необходимо, чтобы выполнялось неравенство

ф b < sup (--) = - п      sin ф

—<ф<п        '

п

.

Таким образом, найдено еще одно ограничение на b . Неравенство (19) задает область H на прямой 0 b .

Объединяя (13) и (19) получаем, что при b е (-А,-п) и (0,+ю)      (20)

уравнение (2) неустойчиво.

Рассмотрим уравнение (14) при k ^ 0. Для того чтобы сделать вывод, что (20) – область неустойчивости уравнения (2) на прямой 0b , следует показать, что корни уравне- ния (14) при k ^ 0 не изменяют области (20). Существование этих корней следует рассмот- п реть лишь при b е [-—,0]. Однако при

п ф е (0, п) , b е [-—,0], k ^ 0 равенство в

• (14)    невозможно ни при каком конкретном ф .

В итоге, система (11) несовместна при таких ф , b , область в (20) не увеличивается.

Окончательно, учитывая, что b = а а в (7), (20), с помощью теоремы 2 доказана следующая теорема.

Теорема 4. Область

{ а а : а ае ( -а , - ^п ) J (0, +а )}

– область неустойчивости H уравнения (2) на прямой 0( а а ) .

§ 2. Область асимптотической устойчивости

Покажем с помощью теоремы 2, что (3),

„  ,    . п .

или S = {b: b е (-—,0)} , - область асимпто- тической устойчивости уравнения (2) на пря- мой 0b . Для этого следует записать систему

' v ⁽ф) = ⁰ и ( ф ) >  0 ,

ф е [0,2 п ] ,

с функциями (9).

Основные преобразования этой системы такие же, как в §1 приводящие к системе (11). Ограничения на параметр b получаем, находя такие ф е [0,2п], при которых имеет место система sin(ф + b sin ф) = 0

‘                                         ,    (21)

• 1    - e b cos ^ф . _COs( ф ₊ b sin ф ) >  0 причем одновременно для всех найденных ф .

Теорема 3 об уменьшении промежутка для ф имеет место и здесь, поэтому считаем, что ф е [0, п ] .

ф = 0 уравнению в (21) удовлетворяет, при ф = 0 неравенство в (21) принимает вид и(0) = 1 - eb > 0, или b < 0,                (22)

что является первым найденным ограничением на b . Неравенство (22) задает область S ₁ .

ф = п уравнению в (21) удовлетворяет, при ф = п неравенство в (21) имеет вид 1 + e - b >  0 и выполнено для V b е R . Дополнительных ограничений к неравенству (22) не появляется.

Рассмотрим систему (21) при фе (0, п) . Уравнение в (21) эквивалентно совокупности уравнений ф + b sin ф = п, j е Z, которую следует рассматривать лишь при четных j, j = 2k, k е Z. При нечетных j, j = 2k +1, к е Z, неравенство в (21) выполняется при Vb е R и при всех существующих ф.

В итоге, система (21) принимает вид ф + b sin ф = 2пк , k е Z b cosф < 0, фе (0, п)

Учитывая (22), неравенство в (23) преобразуется в неравенство cosф > 0, которое уменьшает промежуток для ф, те- п „ перь имеем: ф е (0,—). Таким образом, сис тема (23) эквивалентна уравнению

п ф + b sin ф = 2пк, к е Z, ф е (0,—),(24)

с помощью которого определяется область S .

Рассмотрим уравнение в (24) при к = 0

ф + b sin ф = 0, фе (0,—),(25)

или           b =--ф—.(26)

sin ф

Чтобы уравнение (26) имело корень на про- п.

межутке (0,  ) от b надо потребовать вы полнения условия (см. рис. 1, график функции

У = —— , ф ^{е (0,} п ) )

sin ф b > inf (--) = - -.    (27)

0 < ф < ^п   sin ф     2

Неравенства (22), (27) задают область п,0).

S ₂, S ₂ с S 1 , а именно S₂ = ( —

Отметим, что в случае b е [ — 1,0) уравнение в (25) имеет единственное решение ф = 0 , при котором система (21) выполнена.

п

В случае b е ( ——,— 1) равенство (26)

п возможно при некотором одном ~ е (0,—), при своем фиксированном b , на котором и(ф) = 1 — ebcosф > 0, а уравнение в (25) имеет два корня: ф = 0 и ~ .

Область S содержится в S ₂ . Уравнение п.

• (24)    с к ^ 0 не имеет корней ф е (0, —) при

7   / п всех значениях b е (—— ,0), что означает от сутствие еще каких-либо ограничений на b . п

Промежуток ( — — ,0) не может быть умень-

, п шен, поэтому S = (—— 0) . Итак, учитывая, что b = аю, с помощью теоремы 2 доказана

п

Теорема 5. Область ( — —,0) на прямой

0( а ю ) есть область асимптотической устойчивости S для уравнения (2) .

Замечание 4. Равенство

и (27) возможно лишь при ф

п b = — — в (19)

п

, которое в результате доказательств исключается и в теореме 4, и в теореме 5.

Замечание 5. В точке b = 0 прямой 0 b функция g ( z ) имеет простой нуль z = 1 (единственный) на единичной окружности d U с C ; при этом задача (2) имеет решение x ( t ) = 1 , t >  0 .

п

В точке b = — — прямой 0 b функция g ( z ) имеет простой нуль z = i (наибольший по модулю) на единичной окружности; при этом задача (2) имеет ограниченное решение, не стремящееся к 0 при t ^ +то . В этих случаях уравнение (2) устойчиво (неасимптотически).

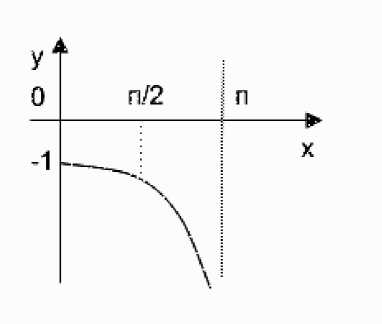
Рис. 1. График функции у =__ sin x