Устойчивость относительно части переменных при постоянно действующих возмущениях "частичного" положения равновесия нелинейных систем дифференциальных уравнений

Во многих прикладных задачах присутствуют постоянно действующие возмущения. При этом часто известны только их наибольшее и наименьшее значения. Отметим, что задача об устойчивости при постоянно действующих возмущениях является классической задачей общей теории устойчивости. Ee решением занимались многие ученые (Г. Н. Ду-бошин [1], И. Г. Малкин [2], В. И. Зу- бов1, Н. Н. Красовский [3], А. А. Тихонов [4], С. И. Горшин [5], А. Страусс и А. Дж. Йорк [6], К. Кордуняну [7] и др.). Во всех указанных работах используются методы теории устойчивости Ляпунова.

В данной работе продолжаются исследования устойчивости при постоянно действующих возмущениях. В отличие от ранее рассматриваемых систем дифференциальных уравнений, нами изучаются системы дифференци- альных уравнений, допускающих «частичное» положение равновесия (см., например, работы [8–9]). Известно, что в настоящее время не сформулировано теорем об устойчивости «частичного» положения равновесия при постоянно действующих возмущениях, что свидетельствует об актуальности данной статьи.

Обзор литературы

Задача об устойчивости при постоянно действующих возмущениях является классической задачей теории устойчивости2–3.

В настоящей статье исследуется вопрос устойчивости «частичного» положения равновесия нелинейных систем, доказывается теорема об устойчивости при постоянно действующих возмущениях, малых в каждый момент времени.

Достаточно полный обзор устойчивости при постоянно действующих возмущениях относительно всех фазовых переменных содержится в моногра-фии4, а также, кроме отмеченных, в работах Р. Габасова [10], В. Е. Гермаидзе и Н. Н. Красовского [11], С. И. Горши-на [12]. С введением устойчивости относительно части фазовых переменных появилась потребность в определении устойчивости при постоянно действующих возмущениях и доказательства соответствующих теорем. Первые теоремы об устойчивости при постоянно действующих возмущениях относительно части фазовых переменных были доказаны А. С. Озиранером5.

Следует отдельно упомянуть работу А. Я. Савченко [13], в которой до- казана теорема об устойчивости при постоянно действующих возмущениях в предположении, что исходная система устойчива.

Материалы и методы

Для получения новых результатов по рассматриваемой тематике были использованы известные результаты теорем об устойчивости положения равновесия нелинейных систем при постоянно действующих возмущениях И. Г. Малкина6 и В. И. Зубова7. Следует отметить, что достаточно полный обзор по указанной тематике содержится в книге А. А. Мартынюка8.

Результаты исследования

С целью получения новых результатов приведем известную теорему об устойчивости положения равновесия нелинейной системы дифференциальных уравнений при постоянно действующих возмущениях.

Для этого рассмотрим нелинейную систему дифференциальных уравнений:

- = f ( t , X ) , f ( t ,0 ) = 0,   (1)

где                                    T x e Rn,f(t,x) = (f (t,x),^f„ (t,x)) .

Предположим, что правые части системы (1) определены в области

Q = { t, x : t >  1 ₀ >  0, x <  H ,0 <  H = const } (2) непрерывными по совокупности переменных и допускают единственность решения задачи Коши при начальных данных из области (2). Здесь и далее:

норма вектора – евклидова, верхний индекс ^T означает транспонирование.

Кроме системы (1), будем рассматривать также систему

X

d; = f ( t , x ) + R ( t , x ) , R ( t ,0 ) * 0, (3) где векторные функции R ( t , x ) являются постоянно действующими возмущениями. Постоянно действующие возмущения будем считать заданными в области (2) и удовлетворяющими тем же условиям, что и f ( t , x )

При постоянно действующих возмущениях R ( t , x ) точно неизвестны⁹. Как уже отмечено, R ( t, 0 ) ^ 0. Будем считать их достаточно малыми, т. е. ||R ( t , x )|| < у , где у >  0 является достаточно малой величиной.

Определение 1

Нулевое решение x = 0 системы (1) называется устойчивым при постоянно действующих возмущениях, если для произвольного е > 0, е <  H существуют числа у >  0 и 5 >  0 такие, что при || ^ ( t , x )|| < y для любых начальных данных || х ₀1< 5 выполняется неравенство | x ( t , 1 ₀, x ₀ )|| <  £ при t >  1 ₀ >  0. Здесь 5 ( t, 1 ₀, 5₀ ) - произвольное решение системы (3), ( 1 ₀, x₀ ) eQ ; величина е > 0 может быть сколь угодно малой¹⁰.

Теорема 1

Пусть для системы (1) существует определенно-положительная функция V (t, x), допускающая бесконечно малый высший предел, полная производная которой по времени t вдоль решений системы (1) есть определенно-отрицательная функция, и если ∂V в области (2) — < N, 0 < N = const, то ∂x нулевое решение системы (1) является

устойчивым при постоянно действующих возмущениях, малых в каждый момент времени.

Данная теорема с доказательством содержится в монографиях И. Г. Мал-

кина и В. И. Зубова11–12

.

Приведем далее определение устойчивости положения равновесия х = 0 системы (1) при постоянно действующих возмущениях относительно части фазовых переменных. _T

Введем обозначение x = ( y , z ) .

Здесь y = ( % i , ^ , x_k ) T , z = ( x_{k + 1}, _ , X n )^т

Определение 2

Нулевое решение системы (1) x = 0 у -устойчиво¹³ при постоянно действующих возмущениях, малых в каждый момент времени, если для любого е >  0, е <  H существуют § > 0 и у > 0 такие, что всякое решение 5с ( t, 1 ₀, x₀ ) и | Х ₀||< § системы (3) удовлетворяет неравенству | Х ( t , 1 ₀, x₀ )|| <  е при любом t ≥ t ₀ и достаточно малом γ > 0, где R ( t , xc ) < у .

В этом определении речь идет об устойчивости при постоянно действующих возмущениях относительно

переменных y 1

Теорема 2

,..., У к .

Пусть для системы (1) существует функция V ( t , x ) , удовлетворяющая условиям¹⁴:

a (IЫР V(t,x )^ b (IIxlI),

dV ( t , x ) dt

где a (|| y ||), b (|| x ||) и c (|| x ||) – непрерывные положительные возрастающие функции, причем а (|| у ||) ^ да при || у || ^ да .

Предположим далее, что система (1) представима в виде

5=^ ( ‘ - У ) •         (4 1 )

dZ = ^f 2 ( t, У . z ) ,         (4 2 )

а система (3) в виде

но действующих возмущениях, малых в каждый момент времени, с наблюдаемой (контролируемой) частью начальных условий фазовых переменных У ^{( 1 )}( t 0 ) = ( У 1 ( t 0 )   У 1 ( t 0 )) T .

Теорема 3

Предположим, что для системы (4 1 —4 2 ) существует функция v ( t , y ) , удовлетворяющая условиям:

dy = fl ( t, y ) + r i ( t, У, z ) ,

dz dt

= f 2 ( t , y,^z

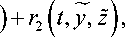
Будем считать, что f (t,0) = 0, rx (t,0, Z)* 0, Г (t, y, Z) < y, 0 < у = const

Введем обозначение y = (y(1)T, y(2)T) ,

a (Ik(1)ll)-v(t,y)- b (Iy(1)ll), dvdy)   5-111 y(1,D-(7)

Bv — „—

— < N ,0 < N <^,(8)

y ^{( 1 )} = ( У 1 , - у/ ) , y ^{( 2 )} = ( y ₊ 1 , - У к ) .

Областью определения систем (41– 42; 51–52) примем

^ 1 = {t , y ^{( 1 )} , y ^{( 2 )} , z : t ^ 1 0 ^ 0,

I y ⁽¹⁾|| < H , || y ⁽⁴< / , | z ||■ <.

При этом также предполагается, что в области Ω₁ правые части систем (4 1 —4 2 ; 5 1 —5 2 ) непрерывны и удовлетворяют условиям единственности решений задач Коши.

Далее в системе (4 1 —4 2 ) будем считать, что y = 0 является «частичным» положением равновесия, т. е. ( 0 T , z^T ) T -«частичное» положение равновесия системы (4₁–4₂) с наблюдаемой (контролируемой) частью начальных условий У 1^V.t 0 ) = ( У 1 ⁽ t 0 ) У / ⁽ t 0 )) T .

Докажем теорему об устойчивости при постоянно действующих возмущениях относительно части _T фазовых переменных у ^{( 1 )} = ( у 1, . „ , у, ) или, короче, об у ⁽¹⁾-устойчивости при постоян-

где a (|| y ⁽¹⁾||), b (|| y ⁽¹⁾||) и c (|| y ⁽¹⁾||) - непрерывные положительные возрастающие функции, причем a ( y ^{( 1 )} j ^ w при | y ⁽¹⁾|| ^w . Тогда нулевое решение систем (4₁–4₂) является y ⁽¹⁾-устойчивым при постоянно действующих возмущениях, малых в каждый момент времени, с наблюдаемой частью начальных условий y 01 = ⁽ y j ⁽ t о ) y_t ⁽ t о ).

Доказательство

Найдем полную производную от функции v ( t , у ) по времени t на решениях системы (5₁). В результате получим:

dv

dv

^dt ( 5 1 )

dt ( 4 1 )

. I д v

+ 1 — , r i ( t , У , ^z

(d y ^v

/

. (9)

С учетом оценки (8) из равенства

(9) получим дифференциальное неравенство

dv

dt

<- K ² + N y .

Выберем y таким, чтобы выполнялось неравенство

dv dt

<- K 1 , K 1 >  о, K 1 =- K ² + N y (10) (Y)

при || y ⁽¹⁾ || <  H, ||y ⁽²⁾ || < w, || z || < ^ и достаточно малом y > 0. Выберем также про-

извольное положительное число ɛ > 0, ɛ ≤ H . При этом допустим, что ɛ > 0 может быть и достаточно малым. Возьмем далее произвольное решение y ( t , 1 ₀, y ₀ ) системы (5 1 ) с || у ₀| <  5 ( s ) Здесь S ( £ ) >  0 не зависит от t ₀, т. к. существуют неравенства (6). Если функция v ( t, у ^{( 1 )} ) является непрерывной и v ( t, 0 ) = 0, то найдется § ( £ ) > 0 такое, что v ( 1 0 ,y ₀ ) < a ( £ ) . Покажем справедливость неравенст^ва v ( t,y ( t,t o , y ₀ )) < a ( £ ) при t >  t o . Допустим, что при t = t ₁ справедливо v ( t,y ( t,1 0 , y ₀ )) = a ( e ) . Однако тогда в силу (10) получим v ( t,y ( t,t ₀, y ₀ )) < 0, v ( t i ,y ( t i , 1 0 , У о )) = a ( £ ) , что противоречит условию (10). Таким образом, a (|| y ⁽¹⁾||) <  v ( t , y ( t , t o , y o )) <  a ( £ ) . В силу того, что функция а (|| у ^{( 1)}|| ) является непрерывной и возрастающей и, кроме того, а (|| у ^{( 1)}|| ) ^ да при || у ⁽¹⁾|| ^ да , то для нее существует обратная функция. Следовательно, справедливо неравенство II У ^{( 1 )} ( t, 1 0 , У о )11 <  ^£ при t ^ t о и достаточно малых 5 ( £ ) >  0 и y > 0.

Доказательство завершено.

Примечание. Доказательство теоремы 3 проведено по алгоритму доказательств теорем 1–2, т. е. по алгоритму доказательства теорем И. Г. Малкина,

В. И. Зубова и А. С. Озиранера: 1) опре- dv деляется область, в которой dt

< 0

на решениях системы (3); 2) с учетом

того, что функция v (t, y(1)) является определенно-положительной, допускает бесконечно малый высший предел, dv и, кроме того, dt

< 0, проверяет-

ся условие || у ^{( 1 )}( t , 1 ₀, у ₀)|| <  £ при t >  1 ₀

и достаточно малых § ( £ ) >  0 и y > 0. Если условия 1) и 2) выполняются, то это и означает y ⁽¹⁾-устойчивость «частичного» положения равновесия y = 0 системы (4₁–4₂) при постоянно дейст-

вующих возмущениях, малых в каждый момент времени.

Обсуждение и заключения

Полученные в данной работе результаты являются развитием теории устойчивости по части фазовых переменных. Достоинством результата является то, что доказанная теорема уникальна, поскольку теорем об устойчивости при постоянно действующих возмущениях «частичного» положения равновесия до сих пор не сформулировано. Доказательство теоремы было проведено по алгоритму доказательства теорем И. Г. Малкина, В. И. Зубова и А. С. Озиранера.

Поступила 18.04.2018; принята к публикации 07.06.2018; опубликована онлайн 20.09.2018

Все авторы прочитали и одобрили окончательный вариант рукописи.