Устойчивость состояния равновесия системы дифференциальных уравнений при решении численным методом Эйлера

В статье получены достаточные условия сохранения устойчивого фокуса системы дифференциальных уравнений при дискретизации методом Эйлера на границе области устойчивости.

Вопрос сохранения типа положения равновесия непрерывной системы при замене ее разностной схемой изучался в работе [1]. Ниже предложен способ решения подобной задачи, основанный на теории критического случая для систем конечно-разностных уравнений. Рассмотрим систему второго порядка x = Ax + F(x), (1)

где х = (xi,x2y,F = (Fi,F2Y, Fi, F2 - аналитические, достаточно гладкие функции, разлагаются в ряды, начиная с членов не ниже второго порядка; А - постоянная матрица соответствующей размерности. Пусть поло жение равновесия системы (0,0) - устойчивый фокус, т. е. собственные значения матрицы А равны Д112 — <х ± i^, а < 0, 3 Y 0.

Заменой х = Sq, где S - неособая матрица, такая, что

S^AS = J = f д )

систему (1) приведем к виду q = Jq+G(q),          (2)

где q = (м)', G = (Gi, G2)'

Ниже даиа разностная схема Эйлера для

уравнения (2)

иметь вид

q(n + 1) = (Е + ftJ)q(n) + №(q(n)),  (3)

пени {0}.

Здесь Л - шаг дискретизации, q(O) = х(0). Собственные числа матрицы линейного приближения равны £1,2 = (l+ha)± ih,3 — 7^e:Elv\ где 7 — V(1 + het)² + h²3², cosy — _s 7

КЗ smy = — ■ 7

Рассмотрим случай, когда модули собственных значений матрицы линейного приближения системы (3) равны единице, т. е. ,         2а шаг дискретизации п =-----—, Систему a2 -VP"

• (3)    запишем в координатной форме

u(n 4-1) = u(n) cosy — v(n) siny 4-

+ kGi(u(n), v(n)),

(4) u(n + 1) = u(n) siny 4- v(n) cosy 4-

+ кСз^Дп), v(n)).

Сделав замену по формулам

«=^г 0=_ы, ю

получим

y(n+I) =e,v,x/(n) -p/i^P^ytn)^^)),

z(n4 1) = в iVz(n) + /i^<2j(y(n),z(n)), 3=2

где Pj(y,z)= tl a_jpy^}~^pz^p, Qj(y,z) = p=0

= 53 “■jpy^Pz^{3 P}, ^ajpi <4? ^- комплексно сопря-p=0

жепные коэффициенты.

Пусть наименьшая степень функций Pj, Qj является нечетным числом з. В противном случае заменой переменных при выполнении определенных условий эту степень можно исключить [2]. Система (6) будет

y(n+ 1) = е^г*у(п) 4-

4- А 52 ^а»рУ^{в р}(п)г^р(п) 4- -, р=0

г(п + 1) = е-1**г(п) 4-

+ А 52 a^y^p(n)z^{g р}(п) + ... р=О

Исследуем на устойчивость нулевое решение системы (7). Преобразуем ее с помощью новых переменных у = ре19, г = ре-ъв к виду p2(n+ 1) = /(п) 4- 2h52/+1[Re(asp) х р=0

х cos((2p 4-1 — з)У(п) 4- у) 4- Im(aap) х (8)

х sin((2p + 1 - з)0(п) 4- у)] 4- ...

Обозначения Re( ), Im(-) соответствуют действительной и мнимой части комплексного числа. В достаточно малой окрестности нуля для первой разности функции К = р2 на решениях уравнения (8) выполняется неравенство

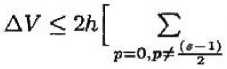
(|Re(a,p)| 4- |Im(asp)|) 4-

4- Re (as;(s_i)/2) cosy 4- Im (as;(,-i)/3) siny

Таким образом, если

Re (as,(s-i)/2) cosy + Im(ae,(s_i)/2) siny <

<- J2 (|Re(a,P)| 4- Ihntasp)!), p=O,p;£l^R то нулевое решение системы (7) асимптотически устойчиво, а положение равновесия системы (3) является устойчивым фокусом.

Пример. Рассмотрим систему дифференциальных уравнений i = х — 2у - 0,56ж3 — 0,бху24-4-0,88т2у 4- 0,16у3, у = 4т — Зу — 0,08а:3 4- 0,2ху2— —0,16т2у — 0,12у3

Собственные значения матрицы линейного приближения - А 1,2 = — 1 ± 2г.

Следовательно, начало координат — устойчивый фокус. Используя преобразование х = 2и + и, у = и + Зи, получим й = —и — 2и — 2u3 — 2 ч и 2 + и2 и 4- и3, и = 2u — v — u3 — uu2 — 2u2-u — 2v3 Перейдем к разностной схеме Эйлера щ(п4 1) — (1 — к^и^тг) — 2/iu(n) + /i(—2н3(тг)— — 2u(n)v2(n) 4- и2(тг)т(п) 4- u3(n)), u(n4- 1) = 2/iu(n) 4- (1 — /i)v(n) 4- Ц—ц3(тг)— — и(п)т2(тг) — 2u3(n)v(n) — 2и3(ц)).

Собственные значения матрицы линейного приближения равны ^1д = (1 — /г) ± i2h.

Исследуем на устойчивость нулевое решение на границе области устойчивости, т. е. при /1 = 2/5. Осуществив замену по формулам it — (ill 4- щ)/2, и — — i(ui — У1)/2, получим ui (п 4- 1) = etv,-ui(n) 4- Ц—2 — i)u2(n)vi(n),

щ(п 4-1) = e",v,ui(n) 4- h(-2 4-i)ui(n)vi(n).

Здесь йз1 = —2 —i, cosy?Re(a.3i) 4- sin^ x x 1ш(яз1) — —2cosp — simp, p = arg(3/54-4- i4/5) t. e. cosip = 3/5, sinp — 4/5 и неравенство (9) выполняется. Значит, положение равновесия исходной системы дифференциальных уравнений сохраняет свой тип при решении методом Эйлера.