Устойчивость термовибрационной конвекции псевдопластической жидкости в плоском вертикальном слое

необходимо учитывать, особенно в связи с интенсификацией технологий производства и переработки нелинейно-вязких текучих сред и повышением требований к ним. Теоретические основы гидродинамики и тепломассообмена в неньютоновских жидкостях при наличии вибраций находятся еще в стадии разработки. При изучении воздействия вибраций на течение нелинейно-вязких сред актуальными становятся задачи, связанные с обсуждением устойчивости стационарных состояний (течений).

Сложные реологические свойства неньютоновских жидкостей приводят к качественному отличию природы устойчивости течений этих жидкостей от ньютоновских. Настоящая работа посвящена исследованию устойчивости термовибрационного конвективного течения, возникающего на фоне высокочастотных вибраций в псевдопластической жидкости, заключенной между двумя вертикальными параллельными плоскостями, нагретыми до разных постоянных температур.

Для ньютоновской жидкости в отсутствие вибраций эта задача рассматривалась в [1–4], где показано, что характер неустойчивости зависит от числа Прандтля. При числах Прандтля, меньших 12,45, и некотором критическом значении числа Грасгофа стационарное плоскопараллельное течение теряет устойчивость по отношению к гидродинамическим возмущениям, имеющим вид вихрей на границе встречных потоков. При числах Прандтля, больших 12,45, неустойчивость возникает в результате развития тепловых волн. Аналогичная связь неустойчивости с числом Прандтля была установлена для псевдо-и вязкопластических жидкостей, описываемых реологическим уравнением Уильямсона, в [5, 6]. В этих работах показано, что число Прандтля, соответствующее смене характера неустойчивости, зависит от нелинейно-вязких свойств жидкости. Усиление неньютоновских свойств приводит к уменьшению значения порогового числа Прандтля таким образом, что при относительно больших числах Прандтля, характерных для псевдо- и вязкопластических сред, наиболее опасными являются тепловые колебательные моды неустойчивости.

Для описания течения неньютоновских жидкостей, вязкость которых есть функция скорости деформаций (скорости сдвига), часто прибегают к степенной реологической модели [7–10]. Устойчивость стационарных конвективных течений степенных жидкостей с ненулевыми начальными вязкостью (в дилатантной жидкости) и текучестью (в псевдопластической жидкости) между двумя твердыми вертикальными параллельными плоскостями, нагретыми до разных температур, изучалась в работах [8, 9]. Показано, что дилатантные свойства жидкостей оказывают стабилизирующее действие, а псевдопластические дестабилизируют течение.

В настоящей работе линейная устойчивость термовибрационного конвективного течения псевдопластической жидкости рассматривается в рамках модели Уильямсона. Выбор модели обусловлен тем, что, будучи предложенной первоначально для описания псевдопластического поведения, она, как впервые показано в [11], может эффективно использоваться для исследования неодномерных течений вязкопластичных сред (см. [11–14]).

Известно, что высокочастотные колебания полости с жидкостью в неоднородном поле температуры вызывают вибрационно-конвективное течение, в котором все физические поля разделяются на пульсационную и осредненную компоненты [15, 16]. Когда период колебаний системы остается много меньше всех гидродинамических времен, а амплитуда смещения в некотором смысле мала, становится возможным применение метода осреднения, позволяющего получить замкнутую систему уравнений для осредненных и пульсационных полей. Вывод уравнений термовибрационной конвекции на основании этого метода был впервые предложен И.Б. Симоненко и С.М. Зеньковской [17]. Систематическое описание основных положений термовибрационной конвекции ньютоновской жидкости приведено в монографии Г.З. Гершуни и Д.В. Любимова [18]. Там же представлены решения линейных задач устойчивости термовибрационного конвективного течения ньютоновской жидкости в бесконечном слое. Для случая продольных относительно слоя вибраций результаты получены в работах А.Н. Шарифулина [19, 20].

Осредненные уравнения термовибрационной конвекции жидкости Уильямсона в высокочастотном приближении сформулированы в [14, 21]. В работе [14] на основании этих уравнений изучалось влияние вибраций на конвективное течение псевдо- и вязкопластических жидкостей, а в [21] — устойчивость жестких состояний слоя вязкопластической жидкости, находящегося в поле высокочастотных вибраций.

• 2.    Уравнения термовибрационной конвекции жидкости Уильямсона

Псевдопластические жидкости относятся к классу обобщенных ньютоновских жидкостей. Для описания псевдопластиков обратимся к реологической модели Уильямсона [11]:

A

^ да '-у ,     '-у

L = —ее..

2      2 ij ji ,

где A и B — реологические константы, ц_да — вязкость при бесконечно большой скорости сдвига.

Уравнения термовибрационной конвекции для обобщенных ньютоновских жидкостей в высокочастотном приближении сформулированы в работах [14, 21]. Они, как и в случае ньютоновской жидкости, описывают медленное осредненное конвективное движение, возникающее на фоне быстрых пульсаций полей скорости, температуры и давления:

д- + ( u V ) u - - 1 V p + 1div т + g в T y + 1 ( a юв ) 2 w V ( T n - w ) ,

d T

— + uV T -%AT,   div u - 0, div w - 0, rot w -V T x n, dt где u, T, p — функции медленного времени t, w — амплитуда пульсационной скорости, т — тензор вязких напряжений, у — единичный вектор (Рис. 1), n — единичный вектор, показывающий направление

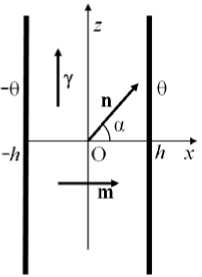
Рис. 1. Вертикальный слой псевдопластической жидкости

вибраций, m — горизонтальный вектор, показывающий направление градиента температуры. Система (2) фактически совпадает с системой уравнений термовибрационной конвекции для ньютоновской жидкости, за исключением вязкого слагаемого div т , вид которого определяется реологической моделью.

При выводе уравнений (2) полагалось, что однородная жидкость целиком заполняет замкнутую полость. Система совершает линейно-поляризованные (возвратно-поступательные) вибрации с амплитудой смещения а и частотой ю в направлении единичного вектора n. Тогда а ю — амплитуда скорости пульсаций. Вибрации считались высокочастотными и малоамплитудными и » {ц„Дрh2), х/h2} (здесь аР9 « h , где h — характерный размер гидродинамических структур, х — коэффициент температуропроводности жидкости, в — коэффициент теплового расширения, 9 — характерная разность температур), а также неакустическими, то есть выполнялись условия

X с » h ,

h » ц „ /(р c ), где X с — длина звуковой волны, соответствующая частоте вибраций, c — скорость

звука. Условие высокочастотности и малоамплитудности вибраций позволило считать жидкость несжимаемой.

В рамках принятых выше предположений осредненная по быстрому времени t- = юt часть тензора вязких напряжений имеет вид:

^т ij

2л

- -1

^{2 п} о

f A

)

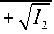
+ ц „   e 0ij

dt - ,

I 2     2 e 0ij e 0 ji ’

e 0 ij = ^{а юв} e wij sin t - + e uij .

Тензор скоростей сдвига в (3) разделяется на две части, одна из них ewij =(d wldxj +8 wj/8xi),

определяется амплитудой скорости пульсаций, а вторая euij = (dui /dxj + duj /dxi), скоростью

осредненного конвективного движения.

В (2), (3) пульсационное течение жидкости полагается невязким. Однако для нелинейно-вязких жидкостей порядок величины вязкого слагаемого в уравнениях для пульсаций обуславливается не только амплитудой пульсационной скорости, но и значением эффективной вязкости жидкости при заданной скорости сдвига. Пренебрежение вязким слагаемым в уравнении для пульсационной скорости может оказаться некорректным.

С этой целью оценим порядок величины вязкого слагаемого, которое в неосредненных уравнениях конвекции жидкости Уильямсона выглядит следующим образом [14]:

1 di ij. р d x i

1 _d_ р d x i

f A

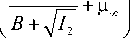
e 0 ij

Для псевдопластических жидкостей вязкое слагаемое (4) имеет порядок величины ц _э ф а ю/ ( р h ²), где в пределе малых скоростей сдвига ц эф - ( Л(В + р „ ) . Сравнение вибрационного и вязкого слагаемых в исходных неосредненных уравнениях [14] дает оценку для частоты пульсаций:

*

to »

Ц эф pOp h ^{2 .}

При выполнении условия (5) вязким слагаемым в уравнениях для пульсаций можно пренебречь.

Для нефти и нефтепродуктов, которые обладают псевдопластическими свойствами, имеем: A = (1 ^ 100) Па, p® 800 кг/м³, ц , = (1 ^ 2000) мПат [22]. Реологический параметр В >  0 и может варьироваться в достаточно широком диапазоне значений. Полагаем, что ц _эф ® 1 Пат, в0 ® 10 - ², h ® 10 ^{— 1} м. Тогда из неравенства (5) получаем, что невязкое приближение для пульсационного поля скорости псевдопластической жидкости справедливо, когда to * » 12,5 рад/с. В псевдопластических жидкостях при малых скоростях сдвига возможно проявление аномально высокой эффективной вязкости ( ц эф >  10 Пат). В этом случае частоты пульсаций, определенные неравенством (5), могут не достигаться в эксперименте. Невыполнение неравенства (5) для заданной частоты пульсаций слоя требует уточнения осредненной системы (2), то есть учета вязких слагаемых для пульсационного поля скорости. В дальнейшем будем считать условие (5) выполненным.

• 3.    Постановка задачи

Рассмотрим бесконечный вертикальный слой жидкости Уильямсона толщиной 2 h , находящийся в поле силы тяжести и ограниченный твердыми идеально теплопроводными границами (см. Рис. 1). На границах слоя зададим постоянные температуры ±0 , равновесный градиент температуры направлен горизонтально вдоль вектора m . Начало координат разместим в центре слоя. Направление осей координат показано на рисунке 1. Полагаем, что вдоль осей y и z слой бесконечен. Он находится в поле линейно-поляризованных высокочастотных вибраций и колеблется в направлении вектора n под углом а к оси x .

Выберем единицы измерения величин: длины — полутолщину слоя h ; времени — h ²р/ц „ ( p — плотность жидкости); скорости осредненного течения — g р0 h ² р/ц „ (Р — коэффициент теплового расширения, g — ускорение свободного падения); температуры и амплитуды пульсационной скорости — 0 ; давления — g Р0 h p .

Уравнения термовибрационной конвекции (2), реологическое уравнение (3) и граничные условия в безразмерной форме примут вид:

an

^ U- + Gr ( U V ) U = —'

ат       ,     .        a

— + Gr ( U V ) T = —A T , at      ^v    ’     Pr

■ V p + Div t + T у + 1Gv ( W V )( T n — W ) ,

rot W = V T x n ,

div U = 0, div W = 0,

x = ±1:

U = 0,    W_x = 0,

T = ±1,

2 n

1 ²n f

^Tij   2n !    ⁺

D 1

e 0 ij

2 7

dt ,

I 2     2 e 0 ij e 0 ji ,

Gv e0ij = Gr ewij sin t — + e"j ’    ewj

d W i dx.

d W j

d X i

e = uij

d U i dx ,

d U

d X i

.

Здесь: U — безразмерная скорость осредненного конвективного течения; W — безразмерная амплитуда скорости пульсаций, а W_x — её проекция на ось x ; на границах слоя выполняются условия прилипания для осредненного потока и условия непротекания для пульсационного течения. Задача (6), (7) содержит пять безразмерных комплексов: число Грасгофа — Gr = g p0p ² h ³/ц² ; вибрационное число

Грасгофа — Gv = (atoPOph/ц„)2, которое характеризует интенсивность вибраций слоя при заданных ц, и 0 ; число Прандтля — Pr = p„/(/p); два безразмерных реологических параметра D = А/(gpOph) и b = Вц„/(gPoph) .

Из (7) видно, что безразмерная эффективная вязкость псевдопластической жидкости определяется выражением (1 + d/(b + ^/I^)). При скорости деформации, стремящейся к нулю, она стремится к (1 + D/b). Безразмерная вязкость ньютоновской жидкости равняется единице. В дальнейшем, при анализе результатов, обсудим зависимости гидродинамических характеристик от параметра D и параметра неньютоновости v = А/(ц„B) = D/b, показывающего отклонение эффективной вязкости при скорости деформаций, стремящейся к нулю, от соответствующего значения для ньютоновской жидкости (единицы).

Модель (7) переходит в ньютоновскую при v ^ 0. Напротив, при больших v ( b ^ « ) эффективная вязкость при малых скоростях сдвига резко возрастает. В этом случае модель (7) описывает вязкопластичную жидкость, где параметр D играет роль предельного напряжения сдвига (предела текучести), а b выступает в качестве регуляризирующего параметра.

В задачах конвекции параметром, определяющим интенсивность течения и влияние возмущений на устойчивость равновесных состояний жидкости, служит число Грасгофа, поэтому правильное нахождение этого параметра для разных типов жидкостей важно, поскольку от этого зависит корректность интерпретации полученных результатов. Число Грасгофа, введенное выше, установлено по вязкости при бесконечно большой скорости деформаций цт . Для обсуждения воздействия псевдопластических свойств жидкости на устойчивость основного течения по отношению к малым возмущениям более правильным представляется рассмотрение модифицированного числа Грасгофа gp0p2h3 _ Gr , (     А У (1 + v)2

I Ц” + R I

V     в )

вычисленного по вязкости при нулевой скорости деформаций (скорости сдвига). Это диктуется тем,

что характерные скорости деформаций, возникающие псевдопластической жидкости, невелики.

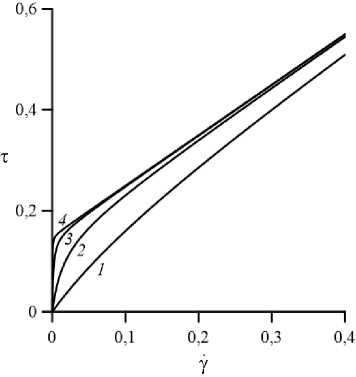
Рис. 2. Зависимость вязких напряжений т от скорости деформаций у = д и]д x при одномерном сдвиговом течении слоя жидкости Уильямсона; кривые построены для D = 0,15 и различных v : 1 (кривая 1 ); 10 ( 2 ); 100 ( 3 ); 1000 ( 4 )

пределе) в возникающем сдвиговом течении вязкость

в слое при медленном конвективном течении

Данное обстоятельство иллюстрируют кривые 1 и 2 на рисунке 2, определяющие зависимость вязких напряжений от скорости деформаций при одномерном сдвиговом течении слоя жидкости Уильямсона со скоростью и ( x ) , где x — поперечная к слою координата. Тангенс угла наклона кривых равняется вязкости жидкости при заданной скорости деформаций. Из рисунка видно, что при небольших v ( v< 100) в области малых скоростей деформаций значение эффективной вязкости близко к (1 + v ). Таким образом, характерной вязкостью псевдопластической жидкости является вязкость при малой скорости деформаций. Отметим, что в работах [8, 9], посвященных решению аналогичной задачи, но без вибраций и с использованием регуляризованной степенной модели, также применялось число Грасгофа, рассчитанное по вязкости при малых скоростях деформации.

При больших v (при вязкопластичном жидкости практически сразу достигает своего

максимального значения ц_т (в безразмерном случае это 1) и далее уже не зависит от скорости деформаций

(см. кривые 3 и 4 на Рис. 2). Поэтому, для вязкопластиков корректнее определять число Грасгофа с помощью величины иу .

Модифицированное число Прандтля, характеризующее свойства жидкости при малых скоростях деформации, находится как P = Pr (1 + v), где параметр v характеризует диссипацию энергии потока за счет вязкости, а Pr — за счет температуропроводности (теплопроводности) жидкости при заданном значении цт.

При рассматриваемых условиях в нелинейно-вязких жидкостях состояние механического равновесия невозможно [21]. Исследуемая задача допускает стационарное решение вида U 0 (0,0, и ₀( x )), T = T ₀( x ), W ₀ = ( ^w o x ,0, ^w o z ), которому соответствует плоскопараллельное осредненное течение (подстрочные индексы x , y и z здесь и далее означают проекции векторных величин на оси координат). Подставляя решение в таком виде в систему (6), (7), после преобразований получим для основного течения уравнения и граничные условия в виде:

-’+1=0,

2ndx2' b + |e0        dxd

e ₀

Gv

=-----sin a sin t + Q_n, T = x , x = ±1: m_n=m_n= 0.

0 v 0                                  00

Gr

Система (10) записана в терминах завихренности и функции тока Q0 = ди0 /5x, и0 = дф0 /5x. При ее получении учтены условия замкнутости пульсационного

J W 0 dx = 0

- 1

и осредненного

J и ₀ dx = 0

- 1

полей

скорости.

Для формулировки линейной задачи устойчивости основного состояния представим все поля в виде сумм основного состояния (подстрочный индекс 0) и малых возмущений (подстрочный индекс 1): U ₀ + U , , W , + W 1 , T ₀ + T 1 , т ₀ + Т 1 , p ₀ + p 1 . Рассмотрим нормальные возмущения вида f1 = f ( x )exp ( ikyy + ikzz -X t ) , периодические вдоль потока, при этом ограничимся их плоским случаем, то есть k_y = 0, u y = w_y = 0 . Для полей возмущений скоростей введем функции тока осредненного и пульсационного течений u z = -ф' , u_x = ik z ф , w_z = - V ' , w_x = ik z V • Линеаризованные уравнения малых возмущений основного состояния в терминах завихренности и функции тока примут вид:

= ( B ₀ + 1 ) Q + 2 B 0 Q' + ( B 0 - k Z ( B ₀ + 1 ) ) Q - ik z Gr и₀ ф + ( ik_z ³Gr u ₀ + 2 k _z ² B 0 + ik_z Gr и 0 ) ф -

• - A T ^msin a + ( ik_zA cos a- 2 A 0 sin a ) T' ' + ( A k z sin a- 1 + 2 ik_zA cos a- A 0 ' sin a ) T ' +

।          1 Gv ।        ।                          1 Gv ]

+ 2 Ak---k cos a v + ik A cos a- Ak cos a--- sin a T —ik —sin av ,

( 0 z 2 Gr z J      z ( 0         0 z 2 Gr J 2 z Gr d T    1 _ _    к2    . _1

И = ф - k2ф,   — = —T - — + ikGriui T - ik.Grф,   v - k2v = -T sin a + ikT cos a, z        dt    Pr (Pr z 0 J z                  zz

VGv 2r Db sin t_               1 2П

A =               т dt ,    Bo =

2nGrJ (b+e0I)2 -        0 2nJ (ь+e01 )2 - x = ±1:   ф = ф' = ^ = T = 0.

• 4.    Численные результаты. Основное течение

Далее обсуждаются только продольные относительно слоя вибрации, то есть a = n/ 2 (см. Рис. 1). Из (10) видно, что вибрации такой ориентации оказывают наибольшее влияние на стационарное течение. Для нахождения основного состояния задача (10) дискретизировалась в соответствии с методом конечных разностей и решалась итерационным методом до достижения заданной точности. Уравнение для функции тока на каждой итерации решалось методом скалярной прогонки. Значения завихренности на границе получались с помощью формулы Тома: Q ₀ |Г = 2 ( ф ₀ |Г -ф ₀ |_r _ 1 ) j h x , где h x — шаг пространственной сетки.

а

б

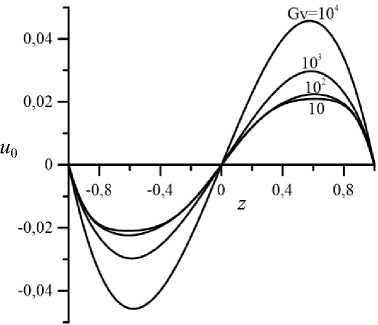
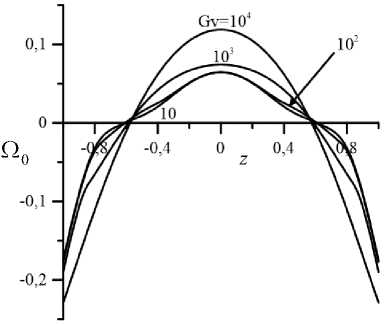
Рис. 3. Профили скорости ( а ) и завихренности ( б ) для псевдопластической жидкости при D = 0,15 , v = 10, Gr = 400

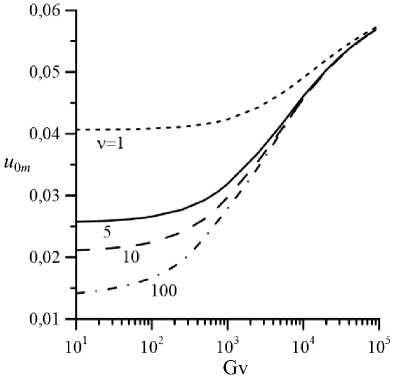
Рис. 4. Зависимость максимума скорости течения псевдопластика от вибрационного числа Грасгофа (параметры жидкости и значение числа Gr аналогичны рисунку 3)

Характерные профили скорости и завихренности основного течения псевдопластика с параметрами D = 0,15, v = 10 при Gr = 400 и различных значениях вибрационного числа Грасгофа показаны на рисунке 3. Завихренность Q ₀ имеет смысл скорости деформаций. С усилением интенсивности вибраций (увеличением Gv) скорость жидкости возрастает, а профили скорости и завихренности приобретают вид, характерный для соответствующих профилей ньютоновской жидкости (см. Рис. 3) [4]. Из рисунка 3 б видно, что характерные значения скорости сдвига отвечают начальному участку реологической кривой 2 на рисунке 2, что подтверждает корректность введения модифицированного числа Грасгофа для описания устойчивости основного течения.

Рисунок 4 демонстрирует рост текучести псевдопластической жидкости с усилением интенсивности вибраций. При очень больших вибрационных числах Грасгофа реология жидкости перестает влиять на структуру и интенсивность течения, кривые на рисунке 4, соответствующие разным v, сближаются. При Gv ^ да скорость основного течения псевдопластической жидкости стремится к скорости ньютоновской жидкости. Это факт подробно обсуждался в работе [14].

• 5.    Численные результаты. Устойчивость течения

Проанализируем результаты численного решения задачи устойчивости стационарного плоскопараллельно течения. Уравнения и граничные условия (11) записывались в конечно-разностной форме, при этом все пространственные производные аппроксимировались центральными разностями, имеющими второй порядок точности. Для вычисления возмущений завихренности скорости Q на границе использовалась формула Тома. Дискретизация (11) привела к алгебраической задаче на собственные значения X CX = FX , где F — комплексная матрица, C — матрица с единицами на главной диагонали и нулевыми остальными элементами, X — вектор, состоящий из неизвестных переменных: X = ( Q , ф , ф , T ) . Решение алгебраической задачи на собственные значения дало значение декремента X = X r + i X i и полей возмущений. Нейтральные возмущения находились из условия Re( X ) = 0. Для решения алгебраической задачи на собственные значения применялся пакет программ, разработанный Д.В. Любимовым, Т.П. Любимовой и В.А. Морозовым [23].

Расчеты показали, что в псевдопластической жидкости, как и в ньютоновской жидкости, тип возмущений и значение критического числа Грасгофа существенно зависят от модифицированного числа Прандтля P (напомним, что здесь ограничиваемся рассмотрением только плоских возмущений). При малых Pr наиболее опасными являются гидродинамические монотонные возмущения, которые представляют собой вихри на границе двух встречных потоков жидкости. С повышением Pr наиболее опасными становятся колебательные возмущения, распространяющиеся в потоке в виде тепловых волн. Увеличение параметра v приводит к уменьшению критических значений G для обоих типов возмущений.

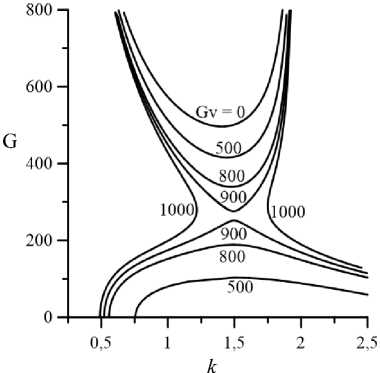
На рисунках 5 и 6 приведены нейтральные кривые монотонных гидродинамических (Pr = 1) и колебательных тепловых (Pr = 100) возмущений (зависимости от волнового числа к ) для v = 0 (ньютоновская жидкость) и v = 1 (псевдопластическая жидкость) при различных значениях вибрационного числа Грасгофа. Гравитационное число Грасгофа здесь и далее модифицировано (см. (8)). Устойчивое состояние стационарного плоскопараллельного течения наблюдается в областях, находящихся между кривыми, построенными для одинаковых значений Gv . В отсутствие вибраций (Gv = 0 ) стационарное плоскопараллельное течение устойчиво при значениях модифицированного числа Грасгофа, отвечающих областям, расположенным ниже соответствующих кривых на рисунках 5 и 6. Значения критических чисел G c и к_с для Gv = 0 при соответствующих значениях v здесь и далее согласуются с полученными ранее значениями для случая, когда вибрации отсутствуют [4, 5]. Нейтральные кривые на рисунке 5 а совпадают с полученными А.Н. Шарифулиным для ньютоновской жидкости [19, 20].

Включение вибраций способствует появлению дополнительной вибрационной моды неустойчивости при относительно малых значениях модифицированного числа Грасгофа. В неоднородно нагретой жидкости в отсутствие поля силы тяжести ( Gr = 0 ) именно вибрационные моды определяют устойчивость стационарных состояний жидкости [15, 16].

На левых ветвях нейтральных кривых вибрационных мод неустойчивости (Рис. 6) имеются характерные изломы, которые согласуются со сменой типа неустойчивости. В точке излома колебательная мода неустойчивости сменяется монотонной, то есть частота нейтральных возмущений скачком обнуляется. На правых ветвях обсуждаемых нейтральных кривых частота колебательных возмущений монотонно стремится к нулю с увеличением волнового числа.

Усиление интенсивности вибрационного воздействия (увеличение Gv ) вызывает дестабилизацию течения жидкости. Области неустойчивости, лежащие выше и ниже кривых, соответствующих одинаковым Gv, расширяются (см. Рис. 5 и 6). При некотором значении Gv нейтральные кривые, сообразующиеся с верхней и нижней модами неустойчивости, соединяются, основное плоскопараллельное течение становится полностью неустойчивым. Из рисунков 5 и 6 видно, что абсолютная дестабилизация основного течения в псевдопластической жидкости наступает при бóльших по сравнению с ньютоновской жидкостью значениях вибрационных чисел Грасгофа.

а

Рис. 5. Нейтральные кривые для монотонных возмущений

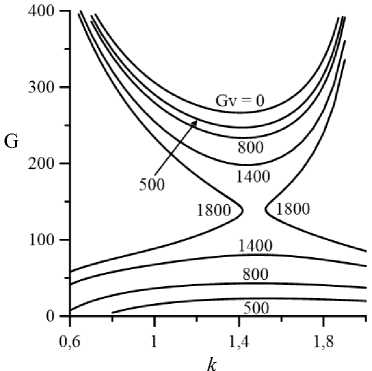
б

( Pr = 1) при различных значениях

Gv для v = 0 (а)

и D = 0,15 , v = 1 ( б )

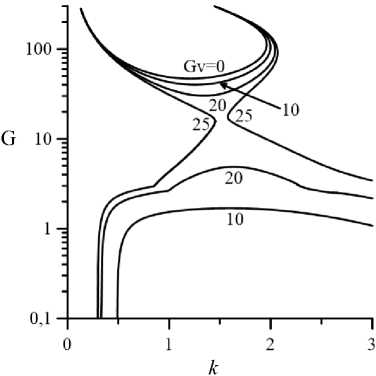
а

Рис. 6. Нейтральные кривые для колебательных возмущений и D = 0,15 , v = 1 (б)

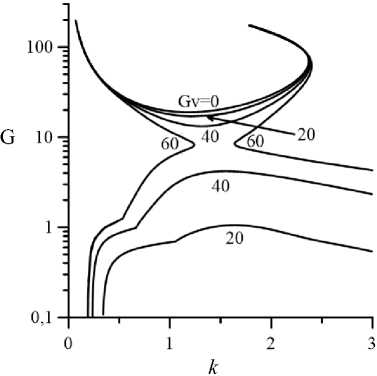
б

( Pr = 100 ) при различных значениях Gv для v = 0 ( а )

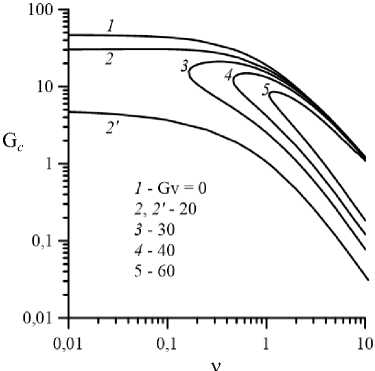
На рисунке 7 приведены зависимости критических модифицированных чисел Грасгофа G _c от параметра неньютоновости v . Слева представлены кривые для монотонных гидродинамических возмущений (Pr = 1), справа — для тепловых колебательных возмущений (Pr = 100). Кривые 1-3 и верхние ветви кривых 4–6 рисунка 7 а сообразуются с гравитационными модами неустойчивости, а кривые 2' , 3' и нижние ветви кривых 4–6 — с вибрационными модами. На рисунке 7 б кривые 1 , 2 и верхние ветви кривых 3–5 отвечают гравитационным модам, а с вибрационными модами соотносятся кривая 2' и нижние ветви кривых 3–5 . Кривые 1 на рисунках 7 а и 7 б при Gv = 0 совпадают с соответствующими кривыми, полученными в работе [5].

Из рисунка 7 видно, что критические значения модифицированных чисел Грасгофа для вибрационных мод неустойчивости (как монотонных гидродинамических, так и тепловых колебательных) монотонно уменьшаются с усилением псевдопластических свойств жидкости. При включении вибраций наблюдается незначительная стабилизация течения с увеличением v относительно гравитационных мод возмущений (см. кривые 2 – 6 на Рис. 7), которая исчезает при интенсификации вибраций. Явление дестабилизации течения псевдопластической жидкости с усилением её нелинейно-вязких свойств при отсутствии вибраций и различных реологических моделях обсуждалось в работах [5, 8, 9]. Большая выраженность псевдопластических свойств жидкости (увеличение v ) приводит к увеличению пороговых значений вибрационного числа Грасгофа, при которых происходит абсолютная дестабилизация течения при рассмотренных типах возмущений.

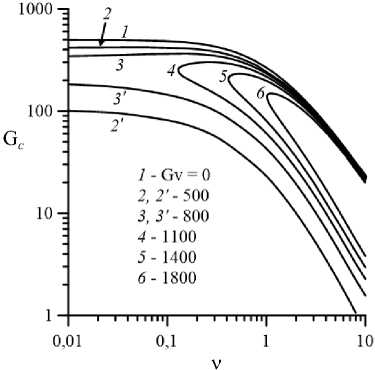
а

Рис. 7. Зависимость критического модифицированного числа Грасгофа от параметра неньютоновости псевдопластической жидкости ( D = 0,15 ) для Pr = 1 ( а ) и Pr = 100 ( б) при различных значениях Gv

б

Таким образом, вибрации, как правило, дестабилизируют основное стационарное течение. Это происходит в силу появления дополнительной моды неустойчивости и увеличения текучести псевдопластической жидкости. Скорость основного течения псевдопластика возрастает по сравнению со случаем течения в отсутствие вибраций (см. Рис. 4), что приводит к росту гидродинамических возмущений, возникающих на границе встречных потоков при малых числах Pr . Взаимодействие относительно быстрого течения с возмущениями в виде тепловых волн при больших значениях Pr способствует росту энергии возмущений и дестабилизации основного течения.

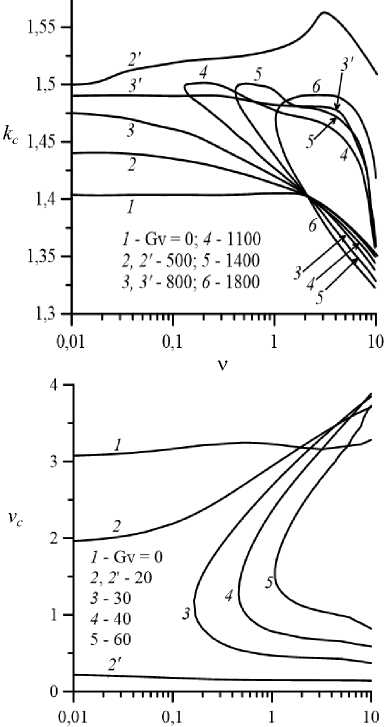
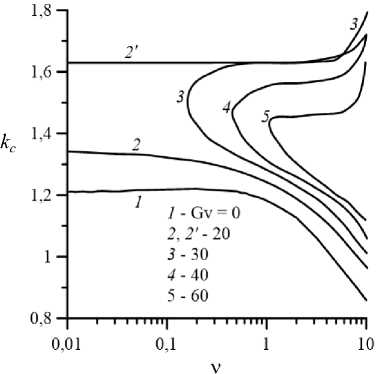
На рисунке 8 показано изменение волновых чисел k_c , соответствующих критическим монотонным гидродинамическим (Рис. 8 а ) и колебательным тепловым (Рис. 8 б ) модам возмущений, в зависимости от параметра неньютоновости v . Вибрационные моды неустойчивости (см. кривые 2' , 3' и верхние ветви кривых 4–6 на рисунке 8 а ; кривую 2' и верхние ветви кривых 3–5 на рисунке 8 б ) являются более коротковолновыми по сравнению с гравитационными модами (см. кривые 1–3 и нижние ветви кривых 4–6 на рисунке 8 а ; кривые 1 , 2 и нижние ветви кривых 3-5 на рисунке 8 б ). При Pr = 1 усиление псевдопластических свойств жидкости вызывает уменьшение волнового числа (увеличение длины волны) критических возмущений для всех мод неустойчивости при всех рассмотренных значениях вибрационного числа Грасгофа, кроме Gr = 500 . При Gr = 500 зависимость критического волнового числа вибрационной моды от параметра неньютоновости носит экстремальный характер (см. кривую 2' на Рис. 8 а ). Отметим, что не столь ярко выраженные максимумы наблюдаются и на кривых 3' , 4 – 6 .

Иной характер зависимости к_с от v имеет место для вибрационных тепловых мод неустойчивости при Pr = 100. Критические волновые числа таких возмущений монотонно растут с усилением псевдопластических свойств жидкости (см. кривую 2' и верхние ветви кривых 3 – 5 на Рис. 8 б ), и скорость роста к_с увеличивается по мере возрастания v , а вслед за этим тепловые гравитационные возмущения становятся более длинноволновыми ( k_c таких возмущений уменьшается, см. кривые 1 , 2 и нижние ветви кривых 3–5 ).

Изменение v_c = к _ic /к_с — фазовой скорости критических колебательных возмущений, с ростом v показано на рисунке 8 в ( к _ic — мнимая часть декремента возмущений, соответствующего G _с ). Видно, что в отсутствие вибраций (кривая 1 ) фазовая скорость тепловых волн в диапазоне исследованных значений параметра v незначительно возрастает с усилением псевдопластичности жидкости. Включение вибраций приводит к уменьшению фазовой скорости тепловых возмущений для v <  2. При наличии вибраций фазовая скорость возмущений, обусловленных действием гравитационного поля (см. кривую 2 и верхние

а

в

б

Рис. 8. Зависимости волновых чисел критических монотонных возмущений – гидродинамических при Pr = 1 ( а ) и колебательных тепловых при Pr = 100 ( б ), а также фазовой скорости тепловых колебательных возмущений ( в ) от параметра неньютоновости при различных значениях Gv и D = 0,15

ветви кривых 3 – 5 ), монотонно увеличивается и при достаточно больших ν превосходит соответствующее значение в отсутствие вибраций. Для вибрационных мод, напротив, с усилением псевдопластических свойств жидкости наблюдается монотонное уменьшение фазовой скорости тепловых возмущений (см. кривую 2' и нижние ветви кривых 3 – 5 ).

Рисунки 5 и 6 свидетельствуют, что наиболее интересный эффект абсолютной дестабилизации термовибрационного конвективного течения получен для отношения чисел Грасгофа Gv/Gr = ( a ω )² βθ/ ( gh ) ≈ 1 . Отношение такого порядка для выбранных в разделе 2 характерных значений βθ , g , h и амплитуды вибраций a ≈ 10 ^{- 3} м достигается при частотах вибраций ω ≈ 10⁴рад/с, что удовлетворяет неравенству (5). К снижению частоты вибраций в несколько раз приводит уменьшение толщины слоя. Например, при h = 10 ^{- 2} м, частота примерно в 3 раза меньше, чем при h ≈ 10 ^{- 1} м. Существенное снижение частоты вибраций при уменьшении толщины слоя возможно в условиях пониженной гравитации. Так, для снижения частоты вибраций на порядок ( ω≈ 10³ рад/с) для толщины слоя h = 10 ^{- 2} м необходимо задать ускорение свободного падения g ≈ 1 м/с². Отметим, что для удовлетворения неравенства (5) в случае h ≈ 10 ^{- 2} м эффективная вязкость жидкости µ _эф не должна превышать значения 0,1 Па·с. Для тонкого слоя при g ≈ 1 м/с² число Грасгофа Gr достигает заявленных в работе значений при µ_∞ ≈ (10 ^{- 2} ÷ 10 ^{- 3}) Па·с.

• 6.    Заключение

В работе на основании уравнений термовибрационной конвекции жидкости Уильямсона изучено влияние продольных высокочастотных линейно-поляризованных вибраций на структуру, интенсивность и устойчивость осредненного конвективного течения псевдопластической жидкости, возникающего в плоском вертикальном слое, ограниченном твердыми идеально теплопроводными границами. Осредненное конвективное течение имеет вид двух встречных параллельных потоков.

Показано, что при усилении интенсивности (увеличении частоты) вибраций нелинейно-вязкие свойства перестают сказываться на осредненном течении псевдопластической жидкости, и профиль скорости приобретает характерный для ньютоновской жидкости вид кубической параболы.

В работе относительно малых нормальных и периодических вдоль слоя возмущений сформулирована линейная задача устойчивости осредненного течения. Расчеты показали, что включение вибраций приводит к дестабилизации течения псевдопластической жидкости. При любых числах Прандтля вибрации вызывают появление дополнительной вибрационной моды неустойчивости, которой соответствуют относительно малые значения модифицированного числа Грасгофа. Для каждого заданного набора реологических параметров модели Уильямсона существуют критические значения модифицированного и вибрационного чисел Грасгофа, при которых осредненное течение полностью теряет устойчивость при рассмотренных типах возмущений. Абсолютная дестабилизация основного течения в псевдопластической жидкости наступает при бóльших по сравнению с ньютоновской жидкостью значениях вибрационных чисел Грасгофа. Тип возмущений и значение критического модифицированного числа Грасгофа существенно зависят от числа Прандтля. При его малых значениях, как и в случае ньютоновской жидкости, наиболее опасными являются гидродинамические монотонные возмущения. С повышением значения числа Прандтля наиболее опасными становятся тепловые колебательные возмущения.

Критические значения модифицированного числа Грасгофа для вибрационных мод неустойчивости монотонно уменьшаются с усилением псевдопластических свойств жидкости (с ростом ν ). При включении вибраций с увеличением ν имеет место незначительная стабилизация осредненного течения относительно гравитационных мод возмущений, которая исчезает при интенсификации вибраций. Усиление псевдопластических свойств жидкости приводит к росту пороговых значений вибрационного числа Грасгофа, которым отвечает абсолютная дестабилизация течения в присутствии возмущений, типы которых обсуждались выше.

Работа выполнена при финансовой поддержке Российского научного фонда (грант № 14-21-00090).