Устойчивые численные методы решения стохастических дифференциальных уравнений в смысле Стратоновича

Многие модели динамических систем в самых различных областях науки: радиотехнике, статистической механике, автоматическом управлении, химии, медицине, теории надежности и т.д., можно описать стохастическими дифференциальными уравнениями (СДУ). Сложность получаемых моделей затрудняет аналитическое исследование решений таких систем. Кроме того, для получения некоторых вероятностных характеристик решения, необходимых на практике, слабо развиты аналитические методы. В этих условиях на первый план стали выходить численные методы.

Как отмечено в работе [1], многие физические задачи, связанные с анализом быстропр от екающих процессов в сильно неравновесных средах, таких как термоядерная, лазерная, газоразрядная и космическая плазма, также можно описать с помощью С ДУ. Причем, предельный переход к модели корректен только для С ДУ в смысле Стратоновича. Актуальность построения устойчивых методов решения С ДУ в смысле Стратоновича обсуждается в работе [2]. В работе [3] было предложено семейство численных методов для решения СДУ в смысле Стратоновича. В данной статье построен устойчивый численный метод из этого семейства. Построенный метод имеет 2-й порядок среднеквадратической сходимости для систем СДУ с одним шумом и 1 -й порядок - в общем случае. Построенный метод рекомендуется для решения задач физики плазмы.

1.    Семейство численных методов решения СДУ в смысле Стратоновича

Пусть на вероятностном пространстве (Q,F,P) заданы: поток ст-алгебр {^}_Ze[or]; «_w-мерный стандартный винеровский процесс w(l), 16 [0,7], согласованный с {FJ_{te[0 г]}, приращения которого w(l + s)-w(l) при s>0 не зависят от ст-алгебры F_t; F_o - измеримый п_у -мерный случайный вектор у₀, независимый с wft) при t > 0, причем F(| у₀ |²) < ОО .

Задача Коши для системы СДУ в смысле Стратоновича ставится следующим образом: найти пу -мерный случайный процесс у(0, для которого tt

ЯО = 7о + J Ry^dr^ j cr(y(r)) °6/w(r),y(O) = yo, 1g [0,7],(1)

о0

где /(y(l)) - измеримая по совокупности переменных n_y -мерная вектор-функция, сг(у(1)) - измеримая по совокупности переменных матричная функция размера п_у xn_w .

Для статистического моделирования траекторий решения систем СДУ в смысле Стратоновича (1) будем использовать семейство численных методов [3] вида

Работа выполнена при финансовой поддержке грантов РФФИ (проекты № 11-01-00282 и № 12-01-00490)

Ди+1 Уп Р\^\ * Pl^l ^"^^ЯххРо ^Qxfix ~^" ЧхЗ^^Сп’             (2)

^1           W^q_x4hG^_n

Go = <7(уп Gx = <т(у„ + ахкх + q3 JhG0£n +           X

2 ад

^2              Wn + «₂к_х + q, 4hG^_n +       ст^;) + ^q₁4hG_x^_n +

( оу)                              2 оу                       2 оу

G2 = о-(у„ +а3кх+ а4к2 + q9 4hGxC„ +

2 ду

Здесь все функции, у которых не указан аргумент, вычисляются в точке у_п , где у_п - значения приближекнного решения системы СДУ (1) в узлах сетки по времени t_n;h - шаг интегрирования; ащулщоу - вещественные параметры метода; ^_й - и_№-мерный вектор независимых гауссовских случайных величин с нулевым математическим ожиданием и единичной дисперсией; ^_й - независимы с у_п . Данное семейство является обобщением методов Розенброка на случай стохастических дифференциальных уравнений. Методы Розенброка являются А-устойчивыми. Наличие параметра а в обобщенных методах Розенброка также позволяет улучшать их свойства устойчивости. Приведем необходимые определения. Для простоты полагаем, что h = t_n+x-t_n=T ! К; п=0, ...,К-Г, t_o=O.

Определение 1 [4]. Численный метод аппроксимирует точное решение задачи Коши для СДУ (1) с порядком р в среднеквадратическом смысле, если для условного математического ожидания выполняется равенство max Е(\ y(tn+x) - уй+1 |2 / уп = yQn ^ = OQipti ), h 0 .

0<и<72-1

Определение 2 [4]. Численный метод сходится с порядком р в среднеквадратическом смысле, если max£(|XO-.rJ2/.Го =УО = °(^Х ^^0 .

1<и<72

Как показано в [4], численный метод решения СДУ имеет р-й порядок сходимости в среднеквадратическом смысле, если он аппроксимирует точное решение с порядком р в среднеквадратическом смысле и также аппроксимирует математическое ожидание с порядком q > р II.

Определение 3 [4, 5]. Численный метод называется асимптотически несмещенным (или устойчивым) с шагом h>0, если при его применении с этим шагом к скалярному линейному СДУ

У (0 = У о - «j yW т + j ст о dw(r\y (0) = у ₀, / е [0,7],                 (3)

о               о где а, ст - вещественные коэффициенты, а > 0, распределение численного решения уп при п —> да сходится к нормальному распределению с нулевым математическим ожиданием и дисперсией <т2 К2а).

Определение 4 [4, 5]. Интервал (х_о,О) называется интервалом асимптотической несмещенности (или устойчивости) метода, если метод является асимптотически несмещенным с любым шагом h>0, для которого -ah& (х_о,О).

Определение 5 [4, 5]. Численный метод называется у -асимптотически смещенным (или у -устойчивым) при 0 если при его применении с фиксированным шагом h к скалярному СДУ (3) с а > 0 распределение численного решения у_п при и —>■ да сходится к нормальному распределению с нулевым математическим ожиданием и дисперсией d , причем

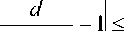
ст2 На

Понятие асимптотической несмещенности (или устойчивости) метода можно определить и для систем СДУ [6].

• 2.    Асимптотическая несмещенность, аппроксимация и сходимость методов

Теорема 1. Семейство численных методов (2) содержит асимптотически несмещенные и у - асимптотически смещенные численные методы. Асимптотически несмещенные численные методы из семейства (2) могут иметь только бесконечный интервал асимптотической несмещенности, и их параметры должны удовлетворять уравнениям

«P=p2q5, PHP2.-V ^Р^-^ а = 1/2.(4)

При аД= p2q5,px + А =1> ^А + Рт)^а2.Р2. = 1/2,1Z4<<2<1Z2(5)

для любого сколь угодно малого у возможно построение у -асимптотически смещенного метода Интервал у - асимптотической смещенности будет определяться из неравенства:

_________№-«2аа) + 1]2

[z2(a-lZ2)2+2z(a-lZ4) + l][2z(a-lZ4) + l] '

Доказательство теоремы основано на применении метода (2) к уравнению (3) и сравнении вероятностных характеристик полученного решения и точного решения (3).

Теперь найдем условия, при которых численный метод из семейства численных методов (2) сходится в среднеквадратическом смысле.

Теорема 2. Семейство численных методов (2) содержит подмножество численных методов, имеющих первый порядок среднеквадратической сходимости для произвольных систем СДУ и второй порядок для систем СДУ с одним шумом, а также в случае систем СДУ с постоянной матрицей ст. Параметры этих методов удовлетворяют уравнениям

А+А=1> АА+АА+А1 + А2 + Аз=1,( p,q2 +            ,             ..               .         ,                        .1

2    + ^^^ + ^3     + ^2) + ^3 А +    + ^ ^ = 2'

Доказательство теоремы основано на сравнении разложений точного и численного решений в ряд Тейлора и применении теоремы сходимости [4].

Построенные численные методы решения СДУ

В работе [3] приведены некоторые численные методы решения СДУ в смысле Стратоновича из семейства (2).

Выделим из семейства методов (2) подсемейство

У_п+1 =у_п+ РК + А^2 + ^q(CT(yP₊₁) + ст(уР ^„,                (⁸)

k_x=\l-ha—\ (ИДу_п) + 4кст<у_пД_п), V ^дУ J

)                       = У»+ ski с пятью параметрами. В записи методов (8) учтена возможность построения у -асимптотически смещенного метода. Параметры методов выберем так, чтобы метод имел 1-й порядок аппроксимации первых двух моментов в общем случае и 2-й - для систем с одним шумом. Приведем три таких метода с параметрами:

а = 3 Z 8, р₂ =1 Z 8, /^ = 7 / 8, q = 3 Z 8, s = 1;

• <2 = 1/3, р₂ = 1 Z6, р_х=5/6, 9 = 1Z 3, s = l;

• <2 = 1/4, р₂ =1/4, р_х =3/4, 9 = 1/4, s = l.

Если параметры численного метода удовлетворяют (4), (6) и (7), то это асимптотически несме- щенный метод с 1-м порядком среднеквадрагической сходимости для произвольных систем СДУ и 2-м - для систем СДУ с одним шумом, а также в случае систем СДУ с постоянной матрицей ст. Приведем пример такого метода:

л₊1 = л + V - @       (Ку„ ) + /(Лн))+^                , yLi =у„+ ^ст(у_п х_п.

(   2 оу) 2                    2

Этот асимптотически несмещенный метод не требует вычисления производной матрицы ст и рекомендуется, в частности, для решения задач, рассматриваемых в [1,2].