Устойчивые явные схемы для уравнения теплопроводности

Рассмотрим одномерное уравнение теплопроводности

Эи _ Э2и dt Эх1'

Обозначим через т шаг по переменной t, через h - шаг по переменной х. Через u_z-i, Ui, щ₊\ обозначим значения функции и при t = to (на оси ж) в точках х_г_\, Xi, Xi₊i, через й_г_1, й_г, й_г+1 обозначим значения функции и при t = to + т в тех же точках (см. рисунок). Зная значения и^ (г = 1, 2, ..., п) нам надо вычислить значения й_г (г = 1, 2, ..., п).

Коэффициенты уравнения (1) и обозначения приведены к безразмерному виду.

Явная схема выглядит так [1, 2]:

ц^ — и_г +

Дг—1    2и^ + U^-j-l

Расчетная схема

(Значения Ui-i, u_t, tz_z+i уже вычислены). Неявная схема выглядит так [1, 2]:

«г

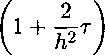
“г-1 + TZz-f-l h?

Т = иг.

Это приводит к решению системы линейных алгебраических уравнений с так называемой трехдиагональной матрицей. Для одномерного уравнения эта схема предпочтительна, ибо явная схема неустойчива при т > Л²/2, в то время как неявная схема устойчива при всех значениях т.

Однако в многомерных случаях неявная схема оказывается не столь удобной. Имея в виду дальнейшие применения численных методов к многомерному уравнению, запишем такую схему

“г и, 2 _      Ui— i + t/z-i-i                                      . .

+ ? =--№--                (4)

Устойчивые явные схемы для уравнения теплопроводности

и перейдем к пределу при т —> 0. Получим обыкновенное дифференциальное уравнение

Йг 2 _ _ Щ—1 4* Ui-щ

Ж ⁺ h²^ “ '    /г²

Его решение

—        ।      \иг-1+мг+1

Ui = u_t- • 9 + (1 - q)-----------

где q = ехр(—2т//г²) < 1. .

С одной стороны, полученная схема явная (й_г определяется по значениям и_г на предыдущем временном слое в соседних узлах), с другой стороны, эта схема абсолютно устойчива. Действительно, полагая

и_г = Аще^ ^г1р (J — мнимая единица),

получаем А = g + (1 — q) со8(г<Д < 1.

Это означает, что значения щ убывают со скоростью геометрической прогрессии.

Если в формуле (6) разложить ехр(—2т//г2) в ряд Тейлора и удержать первые два члена ехр(—2т//г2) « 1 — 2т//г2), то получим обычную явную схему (2). Если 2т//г2 > 1, то схема неустойчива.

Теперь рассмотрим уравнение теплопроводности для двумерного случая в полярной

системе координат

du _ 1 d / du А 1 d²u dt 2 dr \ dr / ~*~ г² dip² '

Обозначим h - шаг по переменной г, т - шаг по переменной t, а- шаг по переменной ip. Явная схема выглядит так

^ik — и_ш +

2п + h 2г_г

Ui+l,k +

2ri — h 2г_г

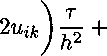
У-цк-Х 4" U₁₇k+1

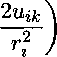
т а²

Здесь г - номер узла сетки по г, к - номер узла сетки по ip. Повторяя процедуру перемещения Щк в Дк, приходим к обыкновенному дифференциальному уравнению где

_/2гг + /г         2ri-h Al u,,k-i 4-и_г,к₊₁

Jik — \   2г- иг+1'к +         иг-Х,к I , 2 +     /   \2•

Обозначим 22

Получаем решение игк =       + (1 - е"^ ^,(12)

т.е. опять возникает устойчивая явная схема.

Однако во многих случаях приходится рассматривать вращающуюся систему координат с постоянной угловой скоростью ш [3].

Тогда уравнение примет вид du du _ 1 d / du dt Ш dip r dr \ dr

1 d²u r² dip²

Вестник ЮУрГУ, №15(115), 2008

А.В. Геренштейн, Е.А. Геренштейн, Н. Машрабов

В этом случае для устойчивости схемы приходим к линейному уравнению в частных производных первого порядка д _ д _    _, uik ш "др Щк + ЦЩк — fik-(14)

Здесь предполагается, что для каждого значения г правая часть /^ является функцией (разумеется, известной) аргумента р.

Решение (явная схема) выглядит так:

й^ = и(<д +шт)е"^т + j e-wJ^p-Р шз^ dp.(15)

о

Имеется в виду, что «(у^ + шт) означают узлы (?, к') сетки, при которых щк = и(у+шт), т.е. значение р + шт попадает в узел (г, к).

Аналогичный смысл имеет выражение / (^ + шз) .

Таким образом, выражение (15) задает явную устойчивую схему для уравнения теплопроводности во вращающейся с угловой скоростью ш полярной системе координат; интеграл в правой части (15) предполагает численное интегрирование заданных в узлах сетки функции.