Уточнение динамических характеристик космических аппаратов в экспериментах на МКС и применение данной технологии при управлении полётом космических аппаратов «Ямал-200»

24 ноября 2003 г. ракетой-носителем (РН) «Протон» были выведены на орбиту геостационарные спутники связи ПАО «Газпром» «Ямал-201» и «Ямал-202» (рис. 1), созданные в кооперации РКК «Энергия» и ОАО «Газком» (ныне АО «Газпром космические системы») (рис. 2). В создании спутников использовались самые современные технологии тех лет. Космический аппарат (КА) «Ямал-201» был установлен в орбитальную позицию 90° в. д. и эксплуатировался в течение 10,5 лет. К преждевременному завершению его использования привёл сбой в работе бортовой вычислительной системы, обусловленный воздействием заряженных частиц. Спутник «Ямал-202» был установлен в рабочую позицию 49° в. д. и успешно отработал в ней до 24 июля 2019 г., передав «вахту» новому спутнику АО «Газпром космические системы» — КА «Ямал-601».

Рис. 1. Старт РН «Протон» с КА «Ямал» (фотография из архива АО ГКС)

а)

б)

Рис. 2. Управление полётом космических аппаратов (КА) «Ямал-200»: а — генеральный директор ОАО «Газком» Н.Н. Севастьянов (в центре слева) рассказывает генеральному конструктору РКК «Энергия» Ю.П. Семёнову (в центре справа) о работе КА «Ямал-200» на орбите; б — зал управления КА «Ямал» (фотографии из архива АО ГКС)

После перевода на КА «Ямал-601» пользователей частотного ресурса в период с 24 июля 2019 г. по 18 ноября 2019 г., КА «Ямал-202» был переведён в позицию 163,5° в. д., в которой и продолжает работу в настоящее время, обеспечивая спутниковыми каналами связи восточную часть нашей страны и территорию до западной части Северной Америки (рис. 3). Эксплуатация КА «Ямал-202» на орбите продолжается уже 20-й год.

Располагая глобальными лучами С- и Ku-диапазонов, охватывавшими почти всю территорию России и значительную часть Европы и Азии (рис. 4, 5), оба спутника были чрезвычайно востребованы различными государственными и бизнес-структурами, а также частными пользователями как в России, так и за рубежом. С использованием КА «Ямал-201» и «Ямал-202» выполнялась ретрансляция различных центральных и региональных теле- и радиопрограмм, осуществлялась передача данных, доступ в Интернет. На базе спутников формировались сети связи различного назначения. Космические аппараты обеспечили связь с труднодоступными регионами, в которых до появления этих спутников отсутствовали какие-либо средства коммуникации.

Успешному использованию этих спутников связи способствовали результаты некоторых технических экспериментов, проведённых на Российском сегменте (РС) Международной космической станции (МКС), 25-летний юбилей запуска которой отмечается в 2023 г. В статье изложены результаты исследований, выполненных на РС МКС в рамках космических экспериментов (КЭ) «Тензор» и «Среда-МКС», которые были использованы при управлении полётом спутников серии «Ямал-200» и способствовали их длительной работе на орбите.

Первый модуль МКС был выведен на орбиту 20 ноября 1998 г. Использование МКС для выполнения космических экспериментов и целевых работ потребовало решения ряда новых задач. Это связано, прежде всего, с большими размерами и массой этой

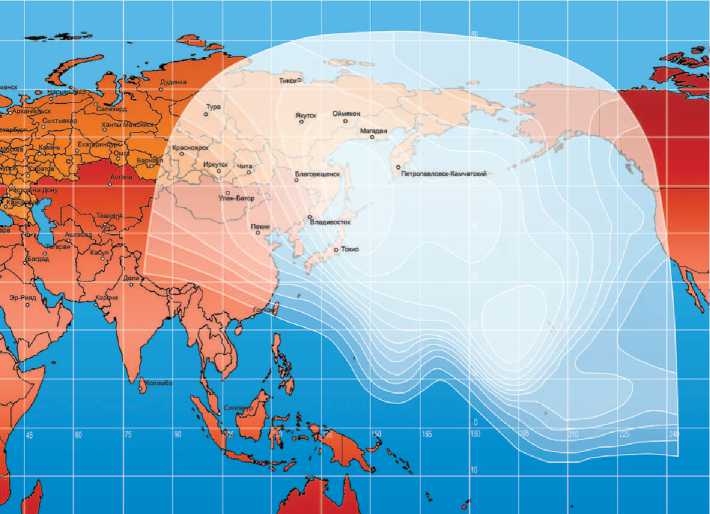
Рис. 3. Зона обслуживания космического аппарата «Ямал-202» с 18 ноября 2019 г. (рисунок из архива АО ГКС)

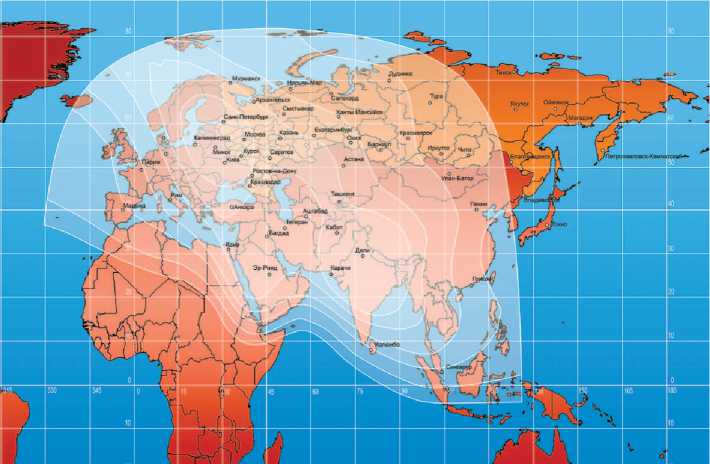
Рис. 4. Зона обслуживания космического аппарата «Ямал-202» в позиции 49 ° в. д. (рисунок из архива АО ГКС)

станции. Причём, в течение полёта характеристики МКС меняются, и их надо уточнять, в т. ч. и для целей управления. Эксперименты «Тензор» и «Среда-МКС» направлены на решение этих задач [1–12]. В этих КЭ определяются динамические характеристики станции, смещение элементов её конструкции и т. д. Знание тензора инерции и других динамических характеристик (массы, положения центра масс) необходимо для управления КА. Важно, чтобы результаты КЭ использовались не только для станции, но и для решения других практических задач. Один из примеров использования результатов экспериментов на МКС связан с эксплуатацией автоматических спутников.

В процессе эксплуатации спутников связи серии «Ямал-200» (рис. 6) технология уточнения тензора инерции КА и прогноза движения КА вокруг центра масс, созданная в экспериментах на МКС, была применена для управления спутниками «Ямал» по прогнозу, благодаря чему КА «Ямал-202» работает на орбите уже 20 лет, и его эксплуатация продолжается [13–17]. Это один из примеров, показывающих и научный, и прикладной результат КЭ на МКС.

^Архангельск

оценка динамических характеристик Международной космической станции

При управлении полётом МКС и решении ряда научных и прикладных задач необходимо достаточно точно знать её динамические характеристики: тензор инерции, параметры аэродинамического момента и т. п. Во время полёта эти характеристики ме

Рис. 5. Зона обслуживания космического аппарата «Ямал-201» в позиции 90 ° в. Д.

(рисунок из архива АО ГКС)                                                    няются, и не всегда их изменение удаётся найти расчётным путём, используя проектные данные. Проводимые на МКС эксперименты «Тензор» и «Среда-МКС» посвящены уточнению фактических значений этих характеристик путём специальной статистической обработки телеметрической информации (ТМИ) с борта станции. Ниже рассматривается один из способов уточнения тензора инерции станции по ТМИ о её ориентации и суммарном кинетическом моменте гиродинов.

Уточнение тензора инерции проводилось ещё для станции «Мир». При этом применялись два способа. Первый состоял в определении неуправляемого вращательного движения станции по данным бортовых датчиков о её ориентации. Определение

Ростов-ка-До ну краеноаар

£

а)

б)

Рис. 6. Спутник связи серии «Ямал-200»: а — внешний вид спутника; б — подготовка к запуску (фотографии

из архива АО ГКС)

движения

сводилось к построению

функций, аппроксимирующих данные измерений или телеметрическую информацию и рассчитываемых вдоль решений полной системы уравнений вращательного движения станции. В результате обработки уточнялись начальные условия движения и некоторые параметры математической модели, в т. ч. пять параметров, характеризующих тензор инерции станции — три угла, задающих направления главных центральных осей инерции в строительной системе координат, и две безразмерных комбинации главных центральных моментов инерции. Приемлемые по точности

оценки получались в результате обработки показаний оптического звёздного датчика и значений кватерниона,

задающего ориентацию станции.

Второй способ уточнения тензора инерции использовал данные измерений суммарного кинетического момента гиродинов, полученные при поддержании неизменной ориентации станции в абсолютном пространстве. Оказалось, что при обработке измерений, выполненных на интервале поддержания одной ориентации, можно оценить только четыре специально выбранные линейные комбинации шести компонент тензора инерции. В частности, если кинетический момент гиродинов измеряется в системе главных центральных осей инерции станции, то можно оценить разности её главных моментов инерции. При совместной обработке измерений, выполненных на нескольких временных интервалах при разных ориентациях станции, можно оценить недиагональные компоненты тензора инерции и разности его диагональных компонент. Оценки, найденные при совместной обработке двух и трёх интервалов, достаточно точно совпадали с оценками, полученными расчётным путём.

Данный подход был использован для уточнения тензора инерции МКС на начальном этапе её полёта. В рамках используемой математической модели станция считается гиростатом, движение центра масс которого по орбите — Кеплерово эллиптическое. Для записи уравнений изменения собственного кинетического момента системы гиро-динов станции, а также уравнений движения МКС относительно центра масс, введём нижеследующие правые декартовы системы координат.

Во второй геоэкваториальной системе координат OX ₁ X ₂ X ₃ эпохи 2000.0 года оси OX ₁ и OX ₃ направлены в точку весеннего равноденствия указанной эпохи и на Северный полюс Земли соответственно. Оси этой системы координат считаем неизменными в абсолютном пространстве.

Строительная система координат Oy ₁ y ₂ y ₃ жёстко связана со станцией. Ось Oy ₁ параллельна продольной оси служебного модуля (СМ) МКС и направлена от его переходного отсека к агрегатному отсеку, ось Oy ₂ параллельна оси вращения солнечных батарей СМ.

Начала этих систем координат находятся в центре масс станции.

Строительная система координат СМ O ′ y ₁ y ₂ y ₃ отличается от системы Oy ₁ y ₂ y ₃ только тем, что её начало O ′ размещается в плоскости седьмого шпангоута СМ.

Далее компоненты векторов и координаты всех точек указываются в системе Oy ₁ y ₂ y ₃ .

Для расчёта радиус-вектора и вектора скорости интегрируются уравнения движения центра масс станции в гринвичской системе координат с учётом нецентральности гравитационного поля Земли и сопротивления атмосферы. Нецентральность поля учитывается с точностью до членов порядка (16,16) включительно в разложении гравитационного потенциала Земли в ряд по шаровым функциям. Атмосфера считается вращающейся вместе с Землёй. Компоненты этих векторов в системе координат Oy ₁ y ₂ y ₃ вычисляются с помощью известных формул перехода.

Компоненты кинетического момента МКС при её движении относительно центра масс имеют следующий вид:

K_i = H_i + _j ∑ ₌ ³ ₁ I_ij ω _j ( i = 1, 2, 3),              (1)

где H_i и ω _j — компоненты собственного кинетического момента системы гиродинов и угловой скорости станции соответственно; I_ij — компоненты тензора инерции станции в строительной системе координат:

I_ij = I_ji ( i , j = 1, 2, 3).

Из моментов внешних сил, приложенных к МКС, учитываются гравитационный M = ( M , M , M ) и вос- g        g 1      g 2 g 3

станавливающий       аэродинамический

Ma = (Ma1, Ma2, Ma3)   моменты. Теорема об изменении кинетического момента станции под действием внешних моментов выражается следующими соотношениями:

.

K ₁ + ω ₂ K ₃ – ω ₃ K ₂ = M_{g 1} + M_{a 1} ;

.

K 2 + ω 3 K 1 – ω 1 K 3 = M g 2 + M a 2 ;          (2)

.

K ₃ + ω ₁ K ₂ – ω ₂ K ₁ = M_{g 3} + M_{a 3} .

Здесь и далее точкой обозначено дифференцирование по времени t .

Компоненты гравитационного момента задаются формулами:

M_{g 1} = ν ∑ x_i ( x ₂ I _{3 i} – x ₃ I _{2 i} );

i = 1

M_{g 2} = ν ∑ x_i ( x ₃ I _{1 i} – x ₁ I _{3 i} );

i = 1

3                                     (3)

M_{g 3} = ν ∑ x_i ( x ₁ I _{2 i} – x ₂ I _{1 i} );

i = 1

= ______3 Me______ v    (x2 + x2 + x2)5/2, где xi — компоненты геоцентрического радиус-вектора центра масс станции в строительной системе координат; μE — гравитационный параметр Земли. Аэродинамический момент можно аппроксимировать двумя способами. Причём второй способ аппроксимации позволяет, помимо тензора инерции, уточнить также координаты положения центра масс станции.

В рамках первого способа аппроксимации аэродинамического момента считаем, что станция имеет форму сферы, центр которой смещён относительно точки О. Тогда выражения для компонент аэродинамического момента примут следующий вид:

M_{a 1} = ρυ( P ₃ υ ₂ – P ₂ υ ₃ );

M_{a 2} = ρυ( P ₁ υ ₃ – P ₃ υ ₁ );

M_{a 3} = ρυ( P ₂ υ ₁ – P ₁ υ ₂ );

υ = υ12 + υ22 + υ32 , где ρ — плотность набегающего на станцию аэродинамического потока (плотность атмосферы в точке О); υi – компоненты скорости центра масс станции относительно поверхности Земли, i = 1, 2, 3; Pi — постоянные коэффициенты. Последние выражения получены в предположении, что атмосфера вращается вместе с Землей.

Подставив в соотношения (2) выражения для величин K_i , M_gi и M_ai , получим следующие уравнения:

.

H = ω H – ω H – I ω^. + ( I – I ) F + I ( F – ω^. ) – I ( F + ω^. ) + I ( G – G ) + E ρυ( P υ – P υ );

• 1       3 2       2 3      11 1       22      33    1      12   2       2       13   3       3       23    3       2                 3 22 3

.

H2 = ω1H3 – ω3H1 – I22 ω.2 + (I33 – I11)F2 + I23(F3 – ω. 3) – I12(F1 + ω. 1) + I13(G1 – G3) + Eρυ(P1υ3 – P3υ1);(4)

.

H = ω H – ω H – I ω^. + ( I – I ) F + I ( F – ω^. ) – I ( F + ω^. ) + I ( G – G ) + E ρυ( P υ – P υ );

• 3       2   1       1   2      33 3       11      22   3      13    1       1       23   2       2       12    2       1                 2 11 2

F ₁ = ω ₂ ω ₃ – ν x ₂ x ₃ ;     F ₂ = ω ₃ ω ₁ – ν x ₃ x ₁ ;    F ₃ = ω ₁ ω ₂ – ν x ₁ x ₂ ;

G1 = ω12 – νx12;   G2 = ω22 – νx22;   G3 = ω32 –

С помощью соотношений I_ij = I_ji из этих уравнений исключены компоненты тензора инерции I_ij при i >  j , и для использования удобных единиц измерения физических величин введён масштабирующий множитель E = 10 ⁹ . В уравнениях (4) кинетический момент измеряется в 10 ³ Н∙м∙с; время — в 10 ³ с; единицей измерения компонент тензора инерции служит 10 ⁶ кг∙м²; единицей измерения аэродинамических параметров — 10 ³ м³; плотность атмосферы рассчитывается в кг/м³.

Уравнения (4) являются замкнутой системой относительно переменных H_i ( i = 1, 2, 3). В этой системе величины I_ij , P_i рассматриваются как параметры. Общее решение этих уравнений представим следующим образом:

H_i = _j ∑ ¹ ₌ ² ₁ F_ij ( t )α _j ( i = 1, 2, 3),                 (5)

где αi = Hi (t0) (i = 1, 2, 3) — начальные условия; t0 — заданный момент времени; α4 = I11; α5 = I22; α6 = I33; α7 = I12; α8 = I13; α9 = I23; α10 = P1; α11 = P2; α12 = P3. Функ- ции Fij(t) определяются начальными задачами для линейных дифференциальных уравнений, не содержащих параметров.

Математическое обеспечение системы гиродинов позволяет в некоторые моменты времени tn (n = 1, 2, …, N); t1H < t2H < … < tNH, получать измерения значений Hi(tnH) компонент её собственного кинетического момента. Результаты измерений этих величин обозначим Hi(n). Если указанные измерения приходятся на отрезок времени, для которого построена аппроксимация движения станции, то с помощью соотношений (5) их можно обработать каким-либо статисти- ческим методом, и α = (α1, α2, …, α12)T. В меньших квадратов определить вектор рамках метода наи-оценкой вектора α

служит его значение, минимизирующее функцию:

Φ(α) = ∑ ^N ∑ ³ п = 1 г = 1

H_i ^{( n )} – ∑ ³ F_ij ( t_n )α _j ²

j = 1

Это значение определяется нормальными уравнениями, которые в данном случае имеют следующий вид:

∑ b_ij α _j = b_i ( i = 1, 2, …, 12),             (7)

j = 1

где b_ij = ∑ ∑ F_ki ( t_n ) F_{k j} ( t_n ); п = 1 k = 1

N 3

b i = ∑ ∑ H i ^{( n )} F ki ( t n ).

п = 1 k = 1

Считаем, что ошибки в измерениях величин H_i ^{( n )} ( i = 1, 2, 3; n = 1, 2, …, N ) независимы, распределены по нормальному закону с нулевым средним значением и стандартным отклонением σ. Тогда оценка αˆ вектора α, определяемая системой уравнений (7), является несмещённой с ковариационной матрицей σ ² B ^–1 , где B — матрица системы уравнений (7). Поскольку значение σ неизвестно, его квадрат — дисперсию ошибок измерений — при расчёте ковариационной матрицы заменим оценкой

^.9

σ ² =

Φ( αˆ) 3 N – 12^.

В рамках второго способа аппроксимации аэродинамического момента используем геометрическую модель станции, согласно которой станция состоит из прямых круговых цилиндров и прямоугольных пластин. Положения этих тел заданы в системе координат Oy ₁ y ₂ y ₃ . Цилиндры служат геометрическими моделями модулей, из которых составлена станция, пластины — моделями солнечных батарей и радиаторов. Тогда выражение для вычисления аэродинамического момента будет иметь следующий вид:

M a = ∑ d i × F i ;

i

M a = ( M a 1 , M a 2 , M a 3 ),                    (9)

где d_i — радиус-вектор геометрического центра тела с номером i относительно точки O ; F_i — действующая на это тело сила аэродинамического сопротивления.

Выражение (9) также получено при предположениях, что атмосфера вращается вместе с Землёй, молекулы воздуха при столкновении со станцией испытывают абсолютно неупругий удар, затенение одних тел другими от набегающего аэродинамического потока не учитывается. В силу двух последних предположений аэродинамический момент, действующий на каждое тело геометрической модели станции и вычисленный относительно геометрического центра этого тела, равен нулю. По этой причине такие моменты в выражении (9) отсутствуют.

Радиус-вектор геометрического центра с номером i определяется следующим образом:

d_i = d_i^b – d_i ⁰ , (10) где d_i^b , d_i ⁰ — координаты геометрического центра тела и центра масс МКС в системе O ′ y ₁ y ₂ y ₃ соответственно.

При использовании второго способа аппроксимации аэродинамического момента система нормальных уравнений (7) записывается с учётом выражений (9) и (10).

Для реализации описанного подхода к оцениванию тензора инерции станции необходимо выполнить восстановление по ТМИ фактического вращательного движения станции. С этой целью использовалось два метода. Первый метод — с использованием сплайновой техники — применяется при сглаживании информации с РС МКС. При этом шаг задания нормированного кватерниона ориентации Q = ( q ₀ , q ₁ , q ₂ , q ₃ ); q ₀ ² + q ₁ ² + q ₂ ² + q ₃ ² = 1, по времени составляет около 1,5 мин. Второй метод — с использованием рядов Фурье — применяется при сглаживании ТМИ с Американского сегмента МКС. При этом шаг задания кватерниона ориентации по времени составляет, как правило, 1 с.

Полученная кватернионная функция нормируется на единицу и служит аппроксимацией вращения системы Oy ₁ y ₂ y ₃ относительно системы OX ₁ X ₂ X ₃ на отрезке t 0 <  t <  t_M . Проекции го ( i = 1, 2, 3) абсолютной угловой скорости системы Oy ₁ y ₂ y ₃ на её собственные оси выражаются через производные этой функции с помощью следующих уравнений:

го = ²⁽ q о ^q i ^- q i ^q 0 + q 3 ^q 2 ^- q 2 ^q 3 );

^го 2 = ²⁽ q 0 ^q 2 ^- q 2 ^q 0 + q 1 ^q 3 ^- q 3 ^q 1 );

^го з =²⁽ q 0 ^q 3 ^- q 3 ^q o + q 2 ^q i ^- q 1 ^q 2 )-

Продифференцировав последние уравнения по времени и подставив в полученные выражения первую и вторую производные нормированной кватернионной функции, можно найти го ₁ , (b ₂ , го ₃ . Это позволяет выполнить расчёт функций F_ij в формуле (5).

Проведённые результаты обработки ТМИ МКС показали принципиальную возможность оценки тензора инерции станции по измерениям суммарного кинетического момента гиродинов. Погрешность оценок при обработке ТМИ составляла менее 7%. Повышение точности достигается как за счёт повышения точности ТМИ, так и за счёт совершенствования используемой при обработке математической модели. Причём, второй путь требует, в первую очередь, повышения точности вычисления действующего на станцию аэродинамического момента.

Обработка результатов, полученных в рамках экспериментов, позволила определить и уточнить ряд характеристик орбитальной станции. Полученные данные использовались при управлении МКС и выполнении на ней целевых программ исследований. Отработанные на орбитальной станции методы и технологии целесообразно использовать также для других аппаратов, в т. ч. исследовательских и прикладных спутников. Это позволяет, в частности, проводить в полёте юстировочные работы для целевой аппаратуры, уточнять динамические и другие характеристики спутников. Уточнение динамических характеристик геостационарного КА даёт возможность построить адекватную модель вращательного движения спутника относительно центра масс (для орбитальных станций эта задача осложняется необходимостью сложного учёта возмущений за счёт действия атмосферы). Наличие адекватной модели вращательного движения позволяет, в частности, построить алгоритмы управления ориентацией без использования датчиков угловых скоростей и непрерывного включения датчиков ориентации, что повышает надёжность и долговечность системы ориентации КА.

управление ка «ямал-200»

с использованием математической модели углового движения

Рассмотренный подход был реализован при оценке тензора инерции геостационарного спутника связи (ГСС) «Ямал», ориентация которого стабилизирована в орбитальной системе координат (ОСК). Точность ориентации спутников «Ямал» не хуже 0,1°. Наличие небольших колебаний ориентации ГСС в ОСК позволило оценить все компоненты тензора инерции.

Как и в случае решения задачи для МКС, ГСС будем считать гиростатом. Центр масс спутника движется по геостационарной орбите. Элементы этого движения определяются по данным радиоконтроля орбиты. В качестве исполнительных органов, используемых на ГСС для управления ориентацией, применяются маховики. Для записи уравнений изменения собственного кинетического момента системы маховиков введём две правые декартовы системы координат. Начала обеих систем поместим в центр масс — точку О .

В качестве базовой системы координат также примем систему OX ₁ X ₂ X ₃ . Под ориентацией спутника в данном разделе будем понимать ориентацию жёстко связанной с его корпусом строительной системы координат Oy ₁ y ₂ y ₃ . В режиме поддержания штатной ориентации ГСС ось Oy ₁ направлена по текущему радиус-вектору, ось Oy ₂ — по текущему вектору линейной скорости.

Положение системы Oy ₁ y ₂ y ₃ относительно системы OX ₁ X ₂ X ₃ задаётся с помощью нормированного кватерниона

Q = ( q ₀ , q ₁ , q ₂ , q ₃ );

q ₀ ² + q ₁ ² + q ₂ ² + q ₃ ² = 1.

Матрицу перехода от системы Oy ₁ y ₂ y ₃ к системе OX ₁ X ₂ X ₃ обозначим || a_ij || ³ _{i , j = 1} , где a_ij — косинус угла между осями OX_i и Oy_j . Элементы этой матрицы выражаются через компоненты Q с помощью известных формул:

a ₁₁ = q ₀ ² + q ₁ ² – q ₂ ² – q ₃ ² ;

a ₁₂ = 2( q ₁ q ₂ – q ₀ q ₃ );

a ₂₁ = 2( q ₁ q ₂ + q ₀ q ₃ )

и т. п. Ниже компоненты векторов и координаты точек указываются в системе Oy ₁ y ₂ y ₃ .

Полёт геостационарного спутника происходит на высоте около 36 000 км, где отсутствует атмосфера Земли. В процессе своего движения спутник либо освещён солнечным светом, либо находится в тени Земли. Причём большую часть полёта он движется по освещённым Солнцем участкам орбиты.

Оценка тензора инерции спутника выполнялась на освещённых Солнцем интервалах орбиты и при движении ГСС в тени Земли. В первом случае из моментов внешних сил, приложенных к спутнику, учитывались гравитационный момент и момент от силы светового давления. Во втором случае учитывался только гравитационный момент.

Компоненты гравитационного момента задавались в соответствии с формулами (3).

Момент от силы светового давления аппроксимируется следующими выражениями:

M_{s 1} = k ( p ₂ e_si – p ₃ e_si );

M_{s 2} = k ( p ₃ e_si – p ₁ e_si );

Ms3 = k(p1esi – p2esi), где k = c–1(r*/∆)2; c — скорость света; r* — средний радиус орбиты Земли; ∆ — расстояние от КА до Солнца; pi — постоянные коэффициенты; esi — компоненты орта ГСС – Солнце. При выводе этих выражений предполагалось, что на интервалах оценки площадь поверхности ГСС, на которую воздействует набегающий световой поток, неизменна, и отражающие свойства поверхности спутника во всех его точках одинаковы. Высокая точность оценки возмущающих моментов, действующих на ГСС, выполненная на таких временных интервалах, позволяет сделать выводы, что принятые допущения вполне оправданны и не окажут существенного негативного влияния на расчётные оценки компонент тензора инерции.

Компоненты кинетического момента спутника в его движении относительно центра масс выражаются в соответствии с формулой (1).

Теорема об изменении кинетического момента ГСС под действием указанных выше внешних моментов выражается следующими соотношениями:

.

K 1 + ω 2 K 3 – ω 3 K 2 = M g 1 + M s 1 ;

.

K ₂ + ω ₃ K ₁ – ω ₁ K ₃ = M_{g 2} + M_{s 2} ;

.

K 3 + ω 1 K 2 – ω 2 K 1 = M g 3 + M s 3 .

Подставив в эти соотношения выражения для величин K_i , M_gi и M_si, получим следующие уравнения:

H ₁ = ω ₃ H ₂ – ω ₂ H ₃ – I ₁₁ ω^. ₁ + I ₁₂ (ω^. ₂ + ω ₁ ω ₃ – ν x ₁ x ₃ ) + I ₁₃ (ω^. ₃ – ω ₁ ω ₂ + ν x ₁ x ₂ ) +

+ ( I ₂₂ – I ₃₃ )(ω ₂ ω ₃ – ν x ₂ x ₃ ) + I ₂₃ [ω ₃ ² – ω ₂ ² + ν( x ₂ ² – x ₃ ² )] + k ( p ₂ e_si – p ₃ e_si );

H ₂ = ω ₁ H ₃ – ω ₃ H ₁ – I ₂₂ ω^. ₂ + I ₂₃ ( ω^. ₃ + ω ₁ ω ₂ – ν x ₁ x ₂ ) + I ₁₂ (ω^. ₁ – ω ₂ ω ₃ + ν x ₂ x ₃ ) +                            (11)

+ ( I ₃₃ – I ₁₁ )(ω ₁ ω ₃ – ν x ₁ x ₃ ) + I ₁₃ [ω ₁ ² – ω ₃ ² + ν( x ₃ ² – x ₁ ² )] + k ( p ₃ e_si – p ₁ e_si );

.

H ₃ = ω ₂ H ₁ – ω ₁ H ₂ – I ₃₃ ω^. ₃ + I ₁₃ ( ω^. ₁ + ω ₂ ω ₃ – ν x ₂ x ₃ ) + I ₂₃ (ω^. ₂ – ω ₁ ω ₃ + ν x ₁ x ₃ ) +

+ ( I ₁₁ – I ₂₂ )(ω ₁ ω ₂ – ν x ₁ x ₂ ) + I ₁₂ [ω ₂ ² – ω ₁ ² + ν( x ₁ ² – x ₂ ² )] + k ( p ₁ e_si – p ₂ e_si ).

С помощью соотношений I_ij = I_ji из этих уравнений исключены компоненты тензора инерции I_ij при i >  j .

Выписанные ниже уравнения используются следующим образом. На некотором отрезке времени длиной не более нескольких часов по ТМИ восстановим фактическое движение спутника относительно центра масс, в т. ч. его угловую скорость и угловое ускорение. В результате уравнения (11) станут замкнутой системой относительно переменных H_i ( i = 1, 2, 3). В этой системе величины I_ij , p_i рассматриваем как параметры. Общее решение этих уравнений, представляется в виде формулы (5).

Математическое обеспечение системы маховиков позволяет в некоторые моменты времени t_n ( n = 1, 2, …, N ) измерять значения H_i ( t_n ) компонент её собственного кинетического момента. Точность определения кинетического момента маховиков КА «Ямал-200» составляет 0,1 Н∙м∙с. Результаты измерений этих величин обозначим H_i ^{( n )} . Если указанные измерения приходятся на отрезок времени, для которого имеются значения кватерниона ориентации, то с помощью соотношений (5) их можно обработать каким-либо статистическим методом, и определить вектор α = (α ₁ , α ₂ , …, α ₁₂ ) ^T . Поскольку вычисляемые по формулам (5) величины H_i ( t_n ) зависят от α линейно, для обработки используем метод наименьших квадратов. В рамках этого метода оценкой вектора α служит его значение, минимизирующее функцию (6).

Это значение определяется нормальными уравнениями (7).

Если ошибки в измерениях величин H_i ^{( n )} ( i = 1, 2, 3; n = 1, 2, …, N ) независимы и имеют одинаковое нормальное распределение с нулевым средним значением и стандартным отклонением σ, то оценка αˆ вектора α является несмещённой с ковариационной матрицей σ ² В ^–1 , где В — матрица системы уравнений (7). Поскольку значение σ неизвестно, его квадрат — дисперсию ошибок измерений — при расчёте ковариационной матрицы можно заменить оценкой (8).

Чтобы реализовать описанный подход к оцениванию тензора инерции спутника, необходимо располагать методом восстановления его фактического движения по ТМИ. Для этого используется метод, основанный на аппроксимации вращательного движения спутника сплайнами.

Анализ полученных результатов свидетельствует о возможности применения описанных моделей и получаемых с их помощью оценок моментов инерции спутника для управления полётом. Повышение точности оценок компонент тензора инерции может идти по пути более точного моделирования момента от силы светового давления, действующего на спутник.

Дальнейшая разработка адекватной математической модели вращательного движения была связана с уточнением модели возмущений от сил светового давления, а также моделей закона изменения суммарного кинетического момента КА и закона изменения кинетического момента маховиков.

Данная технология использовалась затем при управлении ориентацией КА серии «Ямал-200». В полёте КА имели место ситуации, когда некоторые датчики определения ориентации спутника не могли работать устойчиво по каким-либо причинам. Например, возможна ситуация, в которой возникают проблемы в работе блока определения координат звёзд из-за высокой плотности заряженных частиц на орбите КА, вызванной вспышками на Солнце. К недостаткам радиопеленгатора, используемого на КА, можно отнести появление проблемных участков в его работе во время грозы, сильного дождя, снегопада. Следует отметить также невозможность измерения датчиком Земли координат центра Земли в окрестности местной полуночи при прохождении теневых участков орбиты [15]. Для обеспечения поддержания необходимой ориентации КА серии «Ямал-200» при возникновении в полёте указанных проблемных участков был разработан режим «Прогноз» — режим управления ориентацией спутника по прогнозу его углового движения [15–17], который используется по настоящее время при управлении полётом КА серии «Ямал-200».

В этом режиме управление ориентацией спутников осуществляется по прогнозу суммарного кинетического момента. Учитывая, что в расчётах суммарного кинетического момента используются компоненты тензора инерции, меняющиеся в процессе эксплуатации спутника, с целью повышения точности, с помощью изложенного подхода, на теневых и на освещённых Солнцем интервалах орбиты, когда не вращаются солнечные батареи и не работают реактивные двигатели, периодически выполнялась оценка тензора инерции КА.

Выполненная оценка суммарного возмущающего момента, действующего на спутники «Ямал-201» и «Ямал-202» в течение года, позволила повысить точность прогноза суммарного кинетического момента и, как следствие, увеличить длительность поддержания штатной ориентации КА в условиях отсутствия информации от датчиков ориентации с использованием режима «Прогноз» в соответствии с работами [15–17]. На рис. 7 в качестве примера показан результат управления спутником в режиме «Прогноз». С учётом технических особенностей КА «Ямал-201», управление ориентацией во время прохождения теневых участков орбиты, в условиях неработоспособности датчика определения координат центра Земли и ограниченного ресурса звёздного датчика, выполнялось (длительностью до четырёх часов) только в режиме «Прогноз» и в дальнейшем его развитии — «Корректируемый прогноз» [17].

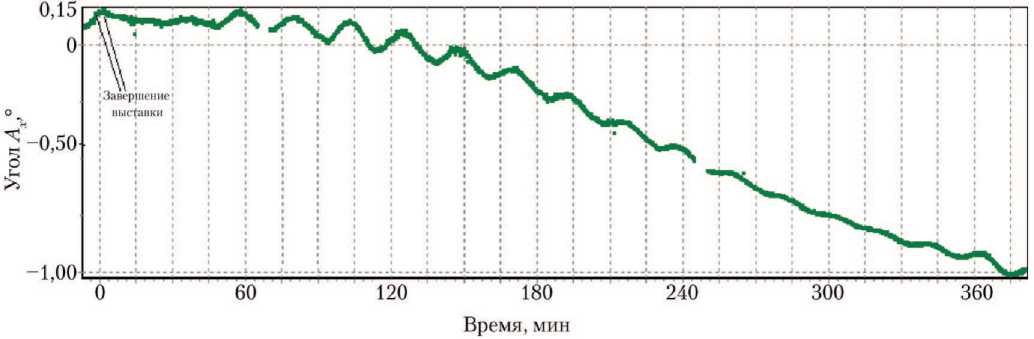
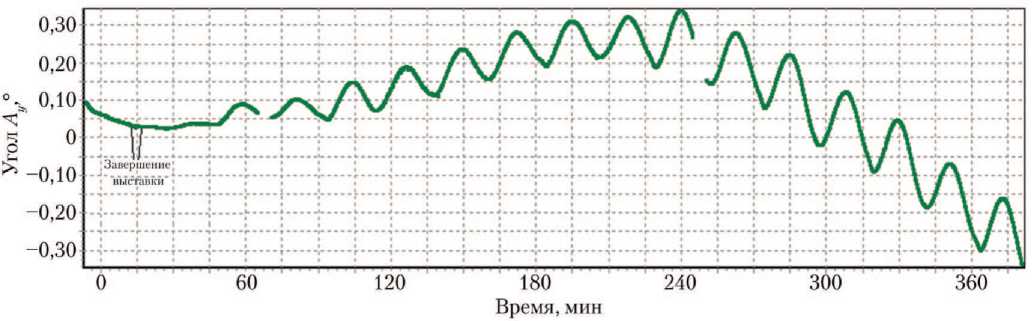
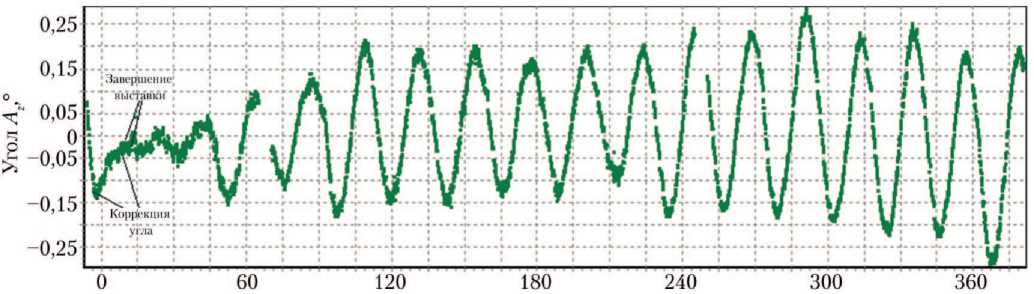
Время, мин

Рис. 7. Управление ориентацией КА «Ямал» в режиме «Прогноз» (рисунки из архива АО ГКС)

В этом режиме длительность управления ориентацией во время отсутствия информации от звёздного датчика (из-за бомбардировки ПЗС-матрицы заряженными частицами во время солнечных вспышек) превышала 30 ч. Являясь резервным режимом ориентации для основных режимов, использующих бортовые датчики ориентации, режим «Прогноз» многократно позволял избежать проблем с предоставлением каналов связи через спутники для пользователей, среди которых — государственные и крупные бизнес-структуры. Режим «Прогноз» основывался на результатах проведённых на МКС технических экспериментов «Тензор» и «Среда-МКС» [13–16].

заключение

Эксплуатация МКС, самого крупного космического объекта в истории освоения космического пространства, потребовала решения большого количества задач, связанных с уточнением в полёте её характеристик: массы, моментов инерции, параметров аэродинамических моментов и т. д. С этой целью на РС МКС были организованы технические эксперименты «Тензор», «Среда-МКС» и др., в рамках которых были разработаны и отрабатывались в полёте методы определения различных характеристик и параметров МКС [1–12]. Данная технология использовалась затем при управлении ориентацией КА серии «Ямал-200» [13–17]. Использование разработанной технологии управления ориентацией КА «Ямал-202» по прогнозу углового движения позволяет продолжать его эксплуатацию уже на протяжении 20 лет.