Уточнение индивидуальной зависимости модуля упругости трабекулярной костной ткани от объемного содержания матрикса

Указанная в заголовке статьи зависимость является необходимой при моделировании процесса адаптации костной ткани, поскольку устанавливает связь механических свойств с параметрами структуры. Известные зависимости, полученные путем решения обратных задач теории упругости для моделей трабекулярной костной ткани, имеют вид степенной функции [5, 6]

E = E м ^ M , (1)

где E _м, г м - модуль упругости материала трабекулы и объемное содержание матрикса соответственно; p – константа, подбираемая экспериментально. Равенство (1) удовлетворяет определяющему соотношению [4], однако не учитывает фундаментальные свойства трабекулярной структуры: 1) ориентацию трабекул (закон Вольфа [12]), влияющую на выбор величины E _м ; 2) принцип минимальности структуры (минимальная плотность при наибольшей прочности [9]). Это обстоятельство является причиной неопределенной методической погрешности равенства (1).

Целью настоящего исследования является уточнение зависимости (1), основанное на учете фундаментальных положений о свойствах структуры живой трабекулярной костной ткани.

Материалы и методы

В соответствии с законом Вольфа в результате структурной адаптации к изменяющейся нагрузке трабекулы костной ткани ориентируются продольной осью вдоль траектории первого главного напряжения. Этим обеспечивается наибольшая прочность структуры, и, следовательно, после завершения процесса адаптации модуль упругости E _м равен модулю упругости трабекулы в продольном направлении E ₁ , тогда как в течение процесса адаптации величина модуля E _м определяется средним значением E _м = E c = ( E 1 + E 2 + E 3 )/ 3 , где E 2 , E ₃ - модули упругости матрикса в поперечных направлениях трабекулы. Модуль упругости E ₁ материала трабекулы (матрикса) в направлении ее продольной оси, определенный измерением твердости сухих образцов, равен 19,4 ГПа, а в поперечном направлении – 15 ГПа [8]. Поскольку влажность снижает жесткость сухого матрикса костной трабекулы не менее чем в 1,2 раза [10], то величины модулей упругости влажной трабекулы в продольном и поперечном направлениях принимаются равными 16,2 и 12,5 ГПа соответственно. Следовательно, получим E c = ( E 1 + 2 E ₂ ) /3 = 13,7 ГПа.

В то же время согласно принципу минимальности структуры трабекулярной костной ткани ( Berjery – Roux ) необходимая наибольшая прочность достигается при ее минимальной массе. Критерий оптимальности, следующий из данного принципа, формулируется следующим образом: «...в эволюционном процессе структура костей приближается к оптимальной с точки зрения критерия

. о * ( X ) .

z (x )= ^ zmax, Vx €Q , (2) P( X )

где о * , p - предел прочности и плотность соответственно [2]». При этом, по нашему мнению, эволюция осуществляется путем изменения клетками таких параметров структуры, как: а) угол между продольной осью трабекулы и направлением касательной к траектории первого главного напряжения; б) объемное содержание матрикса.

Ввиду завершенности эволюции величина z _max в соотношении (2) принимается одинаковой в каждой точке рассматриваемой области О трабекулярной костной ткани и может быть обозначена как z = z . max

Однако в силу погрешностей используемых расчетных моделей структуры и плотности костной ткани критерий z _max имеет разные значения в различных точках области О , т.е. z max = z max ( х ) . В этом случае величина z определяется приближенно как среднее по рассматриваемой области значение

1N z = N Е zmax (j ,                           (3)

где N - число исследуемых точек в области О (рис. 1), а разброс значений z max ( х j ) , j = 1, N относительно z оценивается величиной стандартного отклонения

N 2

77Kz-x (Xj)-z) ■                          (4)

^N j = 1

Материалом данного исследования является аутопсийный фрагмент проксимального отдела бедра взрослого мужчины. Очевидно, что формирование трабекулярной структуры фрагмента завершено, и она является минимальной, поэтому предполагается, что в любой точке фрагмента (см. рис. 1) критерий минимальности имеет максимальное среднее по объему фрагмента значение z .

Формулировка критерия z max = z max ( х ) осуществляется на основании экспериментальных исследований прочности при сжатии образцов губчатой костной ткани, взятых из различных участков проксимального отдела бедра взрослого человека, которые показали, что предел прочности пропорционален локальному модулю упругости костной ткани [3]:

о * ( х j ) = kE ( X j ) , j = 1, N ,                                (5)

где коэффициент пропорциональности k находится из условия того, что при среднем значении модуля упругости губчатой костной ткани 500 МПа предел прочности на сжатие равен 5,5 МПа [11], т.е. k = 0,011.

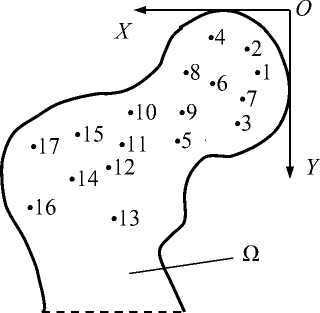
Рис. 1. Схематичное расположение 17 точек, в которых измерялись объемная оптическая плотность, физическая плотность и объемное содержание матрикса трабекулярной костной ткани аутопсийного фрагмента проксимального отдела бедра (рассматриваемая область Ω)

Как отмечалось выше, величина показателя p в равенстве (1) зависит от места отбора образцов из кости (или скелета), поскольку функциональные нагрузки неодинаковы в различных участках кости и стимулируют различные структурные характеристики костной ткани. В связи с этим логично предположить, что показатель p в соотношении (1) является функцией объемного содержания матрикса, например линейной:

Р = a ⁵ м + b ,                                    (6)

где a - константа, подлежащая определению, а константа b = 1 в силу определяющего соотношения для напряжения [4]

6 = 5 м C ( 5 м М ,                             (7)

^/ где 6, £, C (5м) — тензоры напряжений, деформации и жесткости костной ткани соответственно.

Из соотношений (5), (6) следует выражение

6 = kE_x ( 5 м ) a ^{5 м} + b ,                                    (8)

где 6 * , 5 _м — функции x j , j = 1, N .

Объемное содержание матрикса в равенстве (8) определим, полагая костную ткань двухфазной средой, состоящей из твердого матрикса и внутритканевой жидкости. В соответствии с правилом смеси плотность костной ткани

P ( ^ j ) = ⁵ м ( x j ) Р м + ( 1 — ⁵ м ( x j ) ) Р ж

где р _м, р _ж - плотность матрикса (1,78 г/см 3 ) и воды (1,0 г/см 3 ) соответственно [7]. Из

• (9) следует равенство

  ⁵ м ⁽ x j ^{) =}

  
  

  р ( x j ) ^-Р ж

  Р м -Р ж

  
  
  
  

где плотность р ( x j ) костной ткани представляется линейной функцией объемной оптической плотности р_опт ( x j ) , определяемой по уровню яркости белого цвета в точке x j рентгенограммы [1], в виде

р ( x j ) = 0 , 779 + 1 , 337р„ ( x j ) , j = 1, N ,                      (11)

здесь плотность измеряется в г/см3.

Уровни белого и объемная оптическая плотность р_опт ( x j ) , j = 1,17 в точках рентгенограммы фрагмента бедра (см. рис. 1) представлены в табл. 1.

Неизвестная константа а линейного представления (6) ввиду равенств (2) и (8) входит в выражения (3), (4). Следовательно, коэффициент вариации величин z max (- x ) , j = 1, N является функцией а :

C ( a ) =

5 ( a ) z ^{( a} ) ’

Таблица 1

Характеристики рентгенограммы фрагмента бедра в исследуемых точках

Номер точки	X , мм	Y , мм	Уровень белого	ρ опт , кг/м3	ρ, кг/м3	ξ м
1	39	41	122	0,5	1,45	0,45
2	42	34	172	0,59	1,57	0,57
3	51	50	119	0,5	1,45	0,45
4	57	21	170	0,63	1,62	0,62
5	51	51	106	0,42	1,34	0,34
6	67	32	136	0,38	1,29	0,29
7	46	44	163	0,48	1,42	0,42
8	68	27	125	0,32	1,21	0,21
9	73	45	118	0,5	1,45	0,45
10	77	48	90	0,34	1,23	0,23
11	82	53	91	0,38	1,29	0,29
12	89	57	129	0,57	1,54	0,54
13	91	77	133	0,57	1,54	0,54
14	96	64	132	0,57	1,54	0,54
15	102	54	138	0,57	1,54	0,54
16	104	76	140	0,57	1,54	0,54
17	109	68	152	0,62	1,61	0,61

Поскольку коэффициент вариации характеризует относительную величину стандартного отклонения, константу а целесообразно определить как величину оптимальную а _опт, при которой функция (12) достигает минимума, т.е. при a = а _опт критерий минимальности структуры z mx ( X ) имеет наименьшее отклонение от среднего значения z .

Из физических соображений ясно, что с ростом величины объемного содержания матрикса модуль упругости костной ткани должен возрастать, поэтому из соотношения (6) следует условие, ограничивающее область поиска aопт строго положительными значениями вида а гм (Xj )> 0, j = 1, N . (13)

Результаты

Из графика (рис. 2) влияния величины константы a на величину коэффициента вариации С ( а ) (12) распределения критериев минимальности z max ( X j ) , j = 1, N в рассматриваемых точках аутопсийного фрагмента бедра следует, что минимальное значение коэффициента вариации достигается на нижней границе диапазона возможного изменения константы а (0,07–2,07), заданного условием (13), следовательно, a _опт = 0,07.

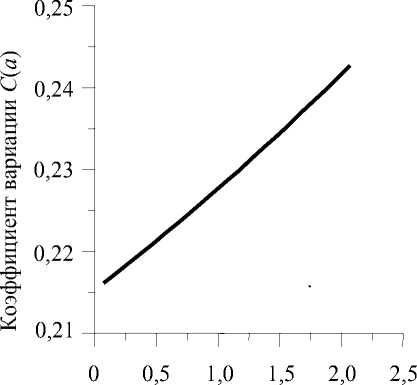
Константа а

Рис. 2. Зависимость коэффициента вариации распределения критерия минимальности трабекулярной структуры в аутопсийном фрагменте проксимального отдела бедра от величины константы а степенной функции (7). Минимальное значение коэффициента вариации, равное 0,216, достигается при а опт = 0,07

Вычисленные при a_опт значения критерия минимальности структуры костной ткани z mx ( х j ) , j = 1, N в исследуемом фрагменте бедра представлены на диаграмме (рис. 3) и характеризуют уровень и неоднородность распределения величины критерия z mx ( х ) . Интересно отметить, что характер неоднородности критерия z mx ( х ) в исследуемом фрагменте кости совпадает с характером неоднородности объемного содержания матрикса (см. табл. 1) в нем.

Среднее значение критерия минимальности структуры z равняется 0,053 МНм/кг, а стандартное отклонение S = 0,011 МНм/кг, что составляет ~21% от среднего значения.

Важно подчеркнуть, что при вычислении распределения критерия минимальности z _max , представленного на диаграмме (см. рис. 3), показатель p согласно соотношению (6) изменяется в интервале 1,014–1,043, т.е. оказывается на ~40% меньшим, чем экспериментально установленная (без учета специфических свойств структуры) величина 1,7 [5]. К тому же величина p = 1,7 реализуется при изменении константы а в интервале 1,1–2,5, т.е. при существенно больших значениях, чем а _опт = 0,07. Как видно из графика (см. рис. 2), в данном интервале изменения константы а относительное стандартное отклонение превышает 22,5% и более. Следовательно, оптимальное значение а _опт = 0,07 обеспечивает наилучшее приближение к z , что обосновывает принятую выше гипотезу об однородности распределения критерия минимальности трабекулярной структуры.

Для оценки влияния учета базовых свойств трабекулярной структуры ( Wolff , Berjery – Roux ) на величину и распределение модуля упругости в аутопсийном фрагменте проксимального отдела бедра выполнялись вычисления при а _опт = 0,07 по трем формулам: 1 - E = E ^м⁷ ; 2 - E = E _с ^ м⁰⁷ ^ “ ; 3 - E = Е^ м,⁰^ (рис. 4).

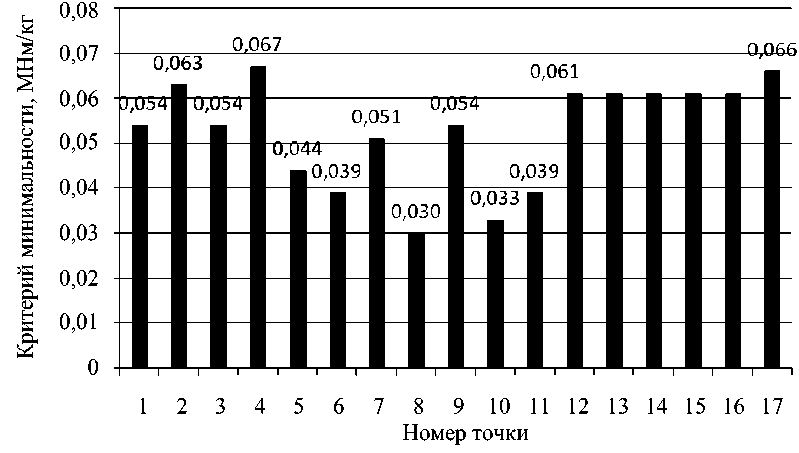
Рис. 3. Значения максимального критерия минимальности трабекулярной структуры zmax в выбранных точках аутопсийного фрагмента проксимального отдела бедра при минимизирующем неоднородность поля критерии zmax и значении константы аопт = 0,07. Среднее значение критерия z = 0,053 МНм/кг, стандартное отклонение S = 0,011 МНм/кг

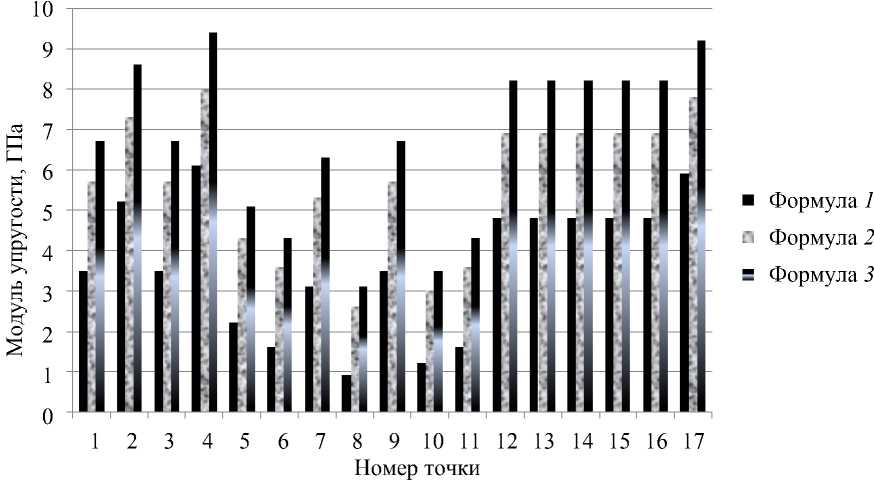
Рис. 4. Распределение модуля упругости в аутопсийном фрагменте проксимального отдела бедра вычислялись при а опт = 0,07 по трем формулам: 1 - E = E c^⁷ ;

2 - E = E cС7^ ; 3 - E = Е , ^ м ' ⁰⁷ ^ ^м

Таблица 2

Средние значения Е и стандартные отклонения (абсолютные 5* и в процентах по отношению к среднему) распределений модуля упругости, представленных на диаграмме (рис. 4)

Формула	E , ГПа	S , ГПа	%
1 - e = e се	3,7	1,6	43,0
2 - Е = Е с.2	5,7	1,7	29,8
3 - Е = Е ^м 07 ^ м	6,8	2,0	29,4

Данные диаграммы (см. рис. 4) показывают одинаковый характер распределения модуля упругости, вычисленного по всем трем формулам. Однако локальная величина модуля упругости существенно зависит от используемой формулы. Из сравнения результатов расчета по формулам 1 и 2 следует, что учет только свойства минимальности трабекулярной структуры 2 приводит к росту уровня локального модуля упругости в интервале ~1,3...2,9 раза в зависимости от величины 1 м в данной точке. Большим значениям из этого диапазона (например, точка 8) соответствуют меньшие значения локального модуля упругости из данного диапазона (для точки 8 в 2,9 раза). Учет ориентации трабекул вдоль траектории главного напряжения 3 увеличивает величину локального модуля упругости, вычисленного по 2 , в E ₁/ E _c раз. Сравнение случаев 2 и 3 со случаем 1 отражает более сильное влияние 1 м в 2 и 3 ввиду меньшей величины показателя а _опт 1 м + 1 (не превышает величины 1,043) у основания 1 м <  1,0 по сравнению с величиной показателя, равного 1,7 в 1 .

Средние значения E и стандартные отклонения (абсолютные S и в процентах по отношению к среднему) распределений модуля упругости (см. рис. 4) представлены в табл. 2.

Из сравнения данных первых двух столбцов табл. 2 следует, что учет только свойства минимальности трабекулярной структуры приводит к увеличению среднего значения модуля упругости E с 3,7 до 6,4 ГПа (в ~1,7 раза) и уменьшению относительного стандартного отклонения с 43,0 до 29,8% (в ~1,4 раза). Рост величины E объясняется ростом локального модуля упругости во фрагменте кости. Существенное снижение стандартного отклонения достигается за счет минимизации относительного стандартного отклонения C ( а ) и применения а _опт.

Из сравнения данных второй и третьей строк табл. 2 видно, что учет ориентации продольной оси трабекул вдоль траектории главных напряжений приводит к росту величины среднего по области модуля упругости E с 5,7 до 6,8 ГПа (в ~1,19 раза). Такое увеличение обусловлено отношением Е 1 / Е c , поскольку Е 1 / Е c = 16,2 /13,7 = 1,19 . При этом стандартное отклонение также возрастает при измерении в абсолютных величинах в ~1,2 раза, а при измерении в относительных величинах (в процентах) незначительно уменьшается.

Таким образом, учет фундаментальных свойств трабекулярной костной ткани как изотропной среды приводит к существенному уточнению экспериментальной зависимости ее модуля упругости от объемного содержания матрикса. Наиболее сильное уточняющее влияние оказывает учет свойства минимальности трабекулярной структуры.

Заключение

Статья посвящена проблеме влияния структуры трабекулярной костной ткани на ее механические свойства. На примере костной ткани аутопсийного фрагмента проксимального отдела бедра изучается влияние базовых свойств структуры на модуль упругости. Костная ткань предполагается изотропным биоматериалом. К базовым свойствам относятся: 1) ориентация продольной оси трабекул вдоль траектории главных напряжений ( Wolff ); 2) свойство минимальности трабекулярной структуры ( Berjery – Roux ).

Результаты выполненных исследований приводят к следующим выводам:

• 1.    Используемые в настоящее время зависимости модуля упругости от объемного содержании матрикса не учитывают влияние базовых свойств структуры, вследствие чего они не обладают достаточной точностью (методическая ошибка вычисления среднего по области значения модуля упругости E составляет не менее 80%).

• 2.    Учет ориентации продольной оси трабекул вдоль траектории главных напряжений приводит к росту величины среднего по области фрагмента модуля упругости на 18%, при этом стандартное отклонение также возрастает (на 10%).

• 3.    Обоснована гипотеза об однородности распределения в костной ткани исследуемой области кости (или скелета) максимального значения критерия минимальности трабекулярной структуры z mx ( -V ) , достигнутого в результате эволюции.

• 4.    Наиболее сильное уточняющее влияние оказывает учет свойства минимальности трабекулярной структуры – приводит к значительному увеличению среднего значения модуля упругости (не менее 54%) и существенному уменьшению относительного стандартного отклонения с 43 до 29,8 ГПа (в 1,4 раза).

• 5.    Уточненная зависимость модуля упругости от объёмного содержания матрикса при физиологической нагрузке имеет вид E = Е 1 ^ м м , где константа а _опт определяется для каждой локализации трабекулярной костной ткани.