Уточнение методики выбора ширины проводников печатных плат на металлическом основании, работающих в условии отсутствия конвекции

В космическом приборостроении получили широкое распространение печатные платы на металлическом основании. Причем такие платы чаще всего работают в условиях отсутствия конвекции. Одной из задач, решаемой в процессе проектирования печатных плат, является выбор ширины печатных проводников ПП. Ширина ПП главным образом определяется током, протекающим через него. Отечественная (ГОСТ Р 53429-2009, РД 50708-91) и зарубежная (IPC-2221A, IPC-2152) нормативно-техническая документация дает указания по расчету ширины ПП. В литературе, такой как [1–4], также имеются указания по расчету ширины ПП. Но все эти указания не касаются печатных плат на металлическом основании. В некоторых публикациях приводятся формулы для расчета ПП печатных плат на металлическом основании, но работающих в условиях естественной конвекции [5]. В [6; 7] описываются методики расчета ширины ПП именно для приборов, работающих на борту космических аппаратов. Однако предлагаемая в них методика дает завышенное значение ширины ПП. Это не позволяет оптимизировать размеры печатных плат.

Автором настоящей статьи была проведена работа, целью которой являлся анализ нагрева упомянутых ПП для уточнения методики расчета ширины ПП для печатных плат на металлическом основании приборов, работающих на борту космических аппаратов.

Для достижения цели были решены следующие задачи:

• •    Построена уточненная математическая модель процесса кондуктивного теплообмена между ПП и металлическим основанием;

• •    Проведен расчет различных, наиболее распространенных, схем расположения слоев печатных плат;

• •    Проведен анализ, и разработана уточненная методика на базе полученных результатов.

1. Описание математической модели

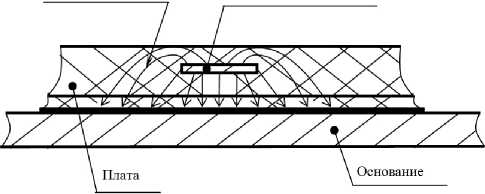
Как и в [6; 7], разделим ПП на внутренние и внешние. В процессе рассмотрено влияние краевых эффектов на внешние и внутренние ПП. На рис. 1 представлены тепловые потоки от ПП к основанию от внешнего ( а ) и внутреннего ( б ). Как видно из рис. 1, тепловые потоки под ПП будут направлены практически перпендикулярно плоскости основания. Ближе к краю ПП у тепловых потоков будет появляться составляющая, параллельная плоскости основания. Это будет происходить за счет разности температур изолятора под ПП и в непосредственной близости от него. За счет этой разности часть тепла будет уходить через изолятор, находящийся в непосредственной близости от ПП. Этот эффект в [6; 7] назван краевым.

ЕЛ^в © Костин А.В., 2021

Тепловые потоки          Печатный проводник

\ Плата                             \ Основание

Тсиловые потоки          Печатный проводник

б

а

Рис. 1. Тепловые потоки от внешнего ( а ) и внутреннего ( б )

Fig. 1. Heat flows from external ( a ) and internal ( b ) conductors

Краевые эффекты для внутреннего и внешнего ПП будут отличаться. Отличие вызвано тем, что от внутреннего ПП отвод тепла осуществляется со всех поверхностей (кроме двух торцевых). На температуру внутреннего и внешнего ПП краевые эффекты будут влиять по-разному. Очевидно одно, что наличие дополнительных тепловых потоков будет снижать температуру ПП.

Для удобства расчетов, как и в работах [6–8], предположим, что тепловыделяющий ПП в рассматриваемой области только один. Других ПП либо нет, либо они не выделяют тепло. Даже если они есть, но тепло не выделяют, их можно не учитывать. Их тепловое сопротивление будет значительно меньше теплового сопротивления изоляционных материалов. Главным образом это связано с разницей в коэффициентах теплопроводностей. Они отличаются на три, в редких случаях – на два порядка. Для изучения взаимного влияния нескольких выделяющих тепло ПП друг на друга необходимо проводить отдельное исследование.

Для расчета значения температуры ПП в стационарном режиме с учетом краевых эффектов необходимо решить следующую систему уравнений теплопроводности:

• д ² T 1 ( x , y ) + д ² T 1 ( x , y ) _ 0

дx2         дy2        ’ x e[-W / 2, W/2], y e[0, h1);

д 2 T 2 ( x , У ) , д ² T 2 ( x , y ) _ 0

дx 2          дy 2’ x e [-W/2, W/2], y e[h, h2);

д2 T (x, y) д2 T (x, y)            г,

---i-^- +i-^- = 0, x e[—W / 2, W / 21, дx2           дy2         ,       [        , y e [h + h2 +... + hi-1, h1 + h2 +... + hi—1 + hi);

д ² T ,.( x , y ) д ² T ,.( x , y )

---j; ---+--- j; ---= 0, x e[— W / 2, W / 2 1

д x ²          д y ²

y ^e[ h i + h + ... + ^h nj — 1 , y _min — ) ;

^д 2 ^T nj⁽ x , y ) ^д 2 ^T nj⁽ x , y )

—---+— --_ 0, дx 2         дy 2

x ^{e[— W} / 2, ^— t j / ² ) , y ^e[ y min j , y max j ) ;

^д 2 ^T nj⁽ x , y )    ^д 2 ^T nj⁽ x , y )

— --+— --_ 0, дx 2         дy 2

x ^e ( t j / 2, ^W / ² ] , y ^e[ y min j , y max j ) ;

д ² T ,.( x , y )    д ² T ,.( x , y )

---nj-₉ ---+--- j; ---_ 0, x e[— W / 2, W / 2 1

д x ²          д y ²

y ^e[ y max j , ^h 1 ⁺ h 2 ⁺ ... ^{+ h} nj ) ;

д ² T ( x , y ) д ² T ( x , y )

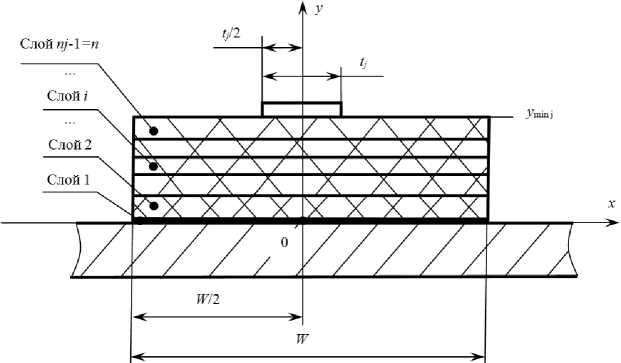
---nl222. +---nl222. _ 0, x e[—W / 2, W / 21, дx2          дy2         ,       [        , J y e [h1 + h2 +... + hn—1, h1 + h2 +... + hn—1 + hn ], где Ti (x, y) - температуры в i-м слое изоляционного материала (в формуле (1) i также принимает значения 1, 2, nj, n) как функция от координат x и y; Tnj(x, y) - температуры в ПП j-го проводящего слоя как функция от координат x и y; qv nj — объемная мощность тепловыделения ПП j-го проводящего слоя; Xп— — коэффициент теплопроводности материала ПП j-го проводящего слоя; W – ширина изоляционных слоев; j – номер текущего проводящего слоя; tj – ширина ПП j-го проводящего слоя; n – общее число слоев изоляционного материала; nj – слой изоляционного материала,

а

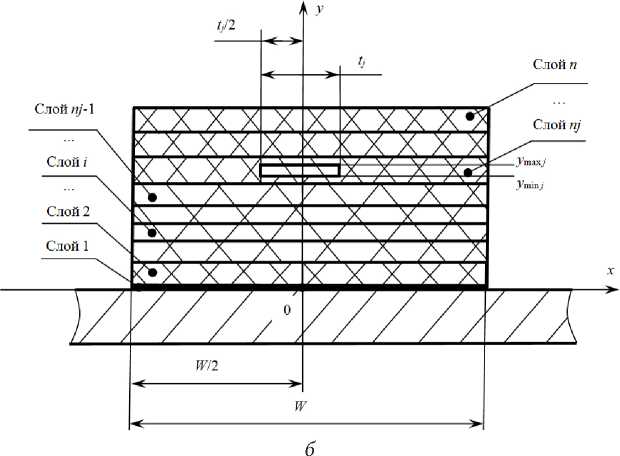
Рис. 2. Геометрия печатной платы с привязкой к системе координат для внешнего ( а ) и внутреннего ( б ) ПП

Fig. 2. The geometry of the printed circuit board with reference to the coordinate system for the external ( a ) and internal ( b ) conductors

в котором находится ПП j -го проводящего слоя; i – номер текущего слоя изоляционного материала ( i = 1... n , в том числе nj ); y min j - значение координаты y для нижней границы ПП j -го проводящего слоя; y _{max j} – значение координаты y для верхней границы ПП j -го проводящего слоя.

Расположение осей системы координат, геометрические размеры и нумерация слоев показана на рис. 2. Поскольку температура прямого ПП, именно такой случай следует рассматривать в первую очередь, не зависит от его длины, то уравнения системы (1) являются двухмерным. В рассматриваемой системе источником тепла является ПП, за его пределами объемная мощность тепловыделения равна нулю. Поскольку режим стационарный, а объемная мощность тепловыделения не равна нулю только в ПП, все уравнения системы (1) однородные, кроме одного. Оно и опи- сывает процессы в ПП. Рассмотрим процесс протекания постоянного тока, как в [6; 7]. Расчетным путем было показано [8], что переменный синусоидальный ток с частотой примерно до 100 кГц, текущий по ПП, можно рассматривать как постоянный ввиду слабой выраженности скин-эффекта. Так что проведенные расчеты будут справедливы и для синусоидального тока низкой частоты. В отсутствие скин-эффекта объемная мощность тепловыделения внутри ПП зависеть от координат не будет. Ее можно найти по формуле qv. nj

= I /p j

22 , h_jt_j

где Ij – значение силы тока, текущего через ПП j-го проводящего слоя, в случае переменного тока это действующее значение; pj - удельное электрическое сопротивление материала ПП j-го прово- дящего слоя; hj – толщина ПП j-го проводящего слоя.

Важно отметить, что на рис. 2 ПП изображен так, что он не примыкает к слоям nj + 1, nj - 1. Это сделано для удобства записи (1). В реальных ПП один из слоев nj + 1 или nj - 1 будет фольгированным диэлектриком. Если фольгированный диэлектрик - это слой с номером nj - 1, то y _min j = h 1 + h 2 + ... + h nj - 1 . Если фольгированный диэлектрик - слой с номером nj + 1, то y _max j = = h + h 2 + ... + h nj . Толщина ПП в общем случае состоит из толщины слоя фольги и толщины слоя гальванической меди. В [6; 7] показано, что их можно представить как единый слой с одинаковыми тепловыми и электрическими характеристиками. При этом ошибка в расчетах будет несущественная. Тогда y max j = У min j ⁺ h nj .

Следует отметить, что система (1) описывает случай симметричного расположения ПП относительно краев печатной платы, то есть расстояние от края ПП до края слоев изоляционных материалов с одной и другой стороны равны.

Для решения дифференциальных уравнений важно задать граничные условия. Для внешних и внутренних ПП они будут отличаться. Рассмотрим граничные условия для внешних ПП. На внешних границах тепловой поток будет отсутствовать

Между изоляционными слоями тепловые потоки и температуры на границе равны:

⁴ i

8 T i ( x , y )

= 4,

8 y

y = h 1 + h ₂ + ... + h i

^{d T} i + 1^{( x} , y ) ' i ^{+ 1}       d y

^, y = h 1 + h ₂ + ... + h i

^T i ^{( x} , ^y )| y = h + h ₂+ .... + h. = ^T i + 1 ^{( x} , ^y )l 12     i

I y = h 1 + h 2 + .... + h i

Между ПП и слоем n тепловые потоки и температуры на границе равны:

⁴ n

8 T_n ( x , y ) 8 y

= 4

Ïj

y = £ hi , x e[- t j /2, t j /2 ] i = 1

^d T nj ^{( x} , У ) 8 y

^, y = £ h i , x e[- t j /2, t j /2 ] i = 1

^T n ⁽ x , y )l У=^Lh i , x e[- t j /2, t, i = 1

j ^{/ 2} ]

= T ( x , y ) n                    .

ⁿj      y = £ h i , x e[- t j /2, t j /2 ]

i = 1

Рассмотрим граничные условия для внутреннего ПП. На внешних границах тепловой поток будет отсутствовать

d T i ( x , y ) d x

x =- W /2

8 T i ( x , y ) d x

8 T i ( x , y ) d x

x =- W /2

8 T i ( x , y ) d x

x = W /2

x = W /2

^d T nj ^{( x} , y ) 8 y

n

У = £ h i + h j i = 1

8 T n ( x , y ) d y

У = £ h i , x e[- W /2, - t j /2 ) i = 1

8 T n ( x , y )

8 y

У = £ h i , x e ( t j /2, W /2 ] i = 1

^d T nj ^{( x} , y ) d x

^d T nj ^{( x} , y ) d x

nn

x = t j /2, y e £ h , £ h i + h j

x =- t j /2, y e £ h i , £ h i + h j

= 0.

У основания

T1( x, 4,=0 = TO, где T0 – температура основания.

8 T_n ( x , y ) 8 y

= 0.

n y=£ hi i=1

У основания справедливо уравнение (4). Между слоями справедливы уравнения (5) и (6). Между ПП и слоем nj тепловые потоки и температуры на границе равны:

⁴ nj

^d T nj ^{( x} , y )

d x

^x = t j ^{/ 2 ,} y ^e[ y min j , у max j )

^d T nj ^{( x} , ^y ) = ^{4 nj}     d x

, x=tj/2,Уe[Уminj, Уmaxj)

⁴ nj

^d T nj ^{( x} , y )

d x

^x =^- t j ^{/ 2 ,} y ^e[ y min j , y max j )

^d T nj ^{( x} , ^y ) = ^{4 nj}     d x

^{, x} =^- t j ^{/ 2 ,} У ^e[ У min j , У max j )

⁴ nj

^d T nj ^{( x} , y )

8 y

y = y min j , ^{x e}[^- t j ^{/ 2 ,} t j ^/2 ]

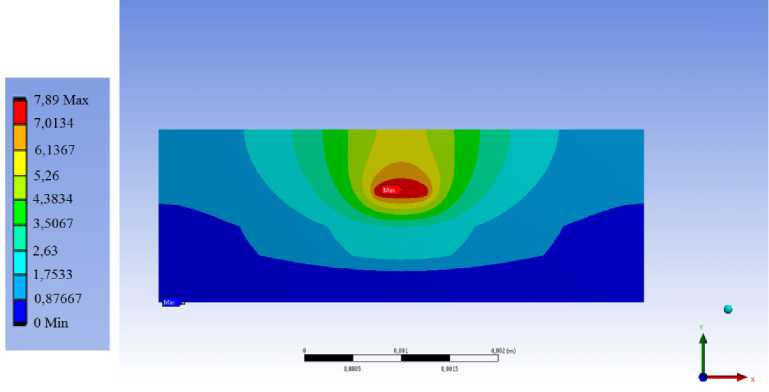
Рис. 3. Результаты расчета для печатной платы типа 2, t = 0,5 мм, t / W = 0,1, ПП третьего проводящего слоя ( j = 3), q v = 3,51 - 10 8 Вт/м³, значения в цветовой шкале даны в ° C

Fig. 3. The calculation results for a type 2 printed circuit board, t = 0,5 mm, t / W = 0,1, conductor of the third conductive layer ( j = 3), q _v= 3,51 - 10 8 W/m³, the values in the color scale are given in ° C

^d T nj ^{( x} , ^У )

^{= Xn} 'v

,

У = У min j , ^{X E}[- t j ^{/ 2 ,} t j ^/2 ]

^ nj

^d T nj ^{( x} . У )

d y

У ^- У max j , ^{X E}[- t j ^{/ 2 ,} t j ^/2 ]

^d T nj ^{( x} , ^У ) ^{= nn} 'v

,

У = У max j , ^{X e}[— t j ^{/ 2 ,} t j ^/2 ]

^j , У^У ^- У min j , ^{x e[-} t j ^{/ 2 ,} t j ^{/ 2} ] ^- T ^{nj( X} ’ ^У ) У - У min j , -[— t j /2, t j /2 ] , T nj ^{( X} , ^У )| У ^- У max j , x e^[- t j ^{/ 2 ,} t j ^{/ 2} ] ^- T ^{nj( x} , ^У ) У - У max j , x e[- t j /2, t j /2 ] , ^j , ^У 1 ^-- t j ^{/ 2 ,} У e^[ У min j , У max j )

^{nj (} , ^У )l ^{x --} t j ^{/ 2 ,} У Е^[ У min j , У max j ) '

T nj ⁽ x , У )|

I x ^- t j ^{/ 2 ,} У e[ У min j , У m_ax j )

- Tnj(X-У)|x-t,/2 Уe[У     У у j' ,y [ У min j , y max j

Уравнения (5)–(8) и (10)–(17) с математической точки зрения записаны несколько неточно, так как определяют температуры и тепловые потоки в точках, где T ( x , у ) и T nj ( x , у ) не существуют одновременно, согласно (1). Правильнее использовать пределы. Однако неточности в записи на результат не повлияют.

2. Результаты расчетов

Решать систему (1) аналитическим методом весьма сложно, особенно при проведении технических расчетов. Целесообразнее воспользоваться численным методом. Для этого используем ANSIS 2019 R1, модуль Steady-State Thermal. T ₀ целесообразно принять равной нулю. Тогда программа будет возвращать значения перегрева A T (разницу между температурами основания и ПП). Причем считать можно в ° C. Разница температур в ° C и К будет одинакова.

Универсальную формулу или график получить не удастся. Схемы расположения слоев разные. Применяются материалы с разными теплофизическими свойствами. Необходимо рассматривать конкретные схемы расположения слоев. Как правило, они типовые, по крайней мере в рамках одного конструкторского бюро (нучно-исследо-вательского института) или конструкторского подразделения. Достаточно просчитать типовые схемы и пользоваться этими результатами. При появлении необходимости применения других схем дополнить результаты расчетов. Если отсутствует специализированое программное обеспечение, можно воспользоваться программами для расчета электрических схем, а рассматриваемую область представить в виде совокупности конечных элементов. Каждому конечному элементу будет соответствовать резистор, сопротивление которого будет равно тепловому сопротивлению этого элемента.

На рис. 3 представлены некоторые результаты расчетов для схем типа 2. Типы – это условные

Табл. 1. Схемы типов печатных плат

Table 1. Schemes of types of printed circuit board

Тип печатной платы Материал изоляционных слоев hi, мкм Xi, Вт/м х К j hПj, мкм 1 (двусторонняя) 2 55 Стеклотекстолит СТФ-2-35-0,25 0,25 0,3 Стеклоткань СТП-4-0,062, 4 слоя 0,248 0,3 1 55 Пленка клеевая ПКС-171 0,08х400 0,08 0,3 2 (4-слойная) 4 55 Стеклотекстолит СТФ-1-35-0,25 0,25 0,3 Стеклоткань СТП-4-0,062, 2 слоя 0,124 0,3 3 35 Стеклотекстолит СТФ-2-35-0,25 0,25 0,3 Стеклоткань СТП-4-0,062, 2 слоя 0,124 0,3 2 35 Стеклотекстолит СТФ-1-35-0,25 0,25 0,3 Эласил 137-182 0,3 1,6 1 55 Стеклоткань СТП-4-0,062, 3 слоя 0,186 0,3 Клей ВК-9 с нитридом бора 0,3 0,9 3 (6-слойная) 6 38 Стеклотекстолит СТФ-1-18-0,15 0,15 0,3 Стеклоткань СТП-4-0,062, 2 слоя 0,124 0,3 5 18 Стеклотекстолит СТФ-1-18-0,15 0,15 0,3 Стеклоткань СТП-4-0,062, 2 слоя 0,124 0,3 4 18 Стеклотекстолит СТФ-1-18-0,25 0,25 0,3 Стеклоткань СТП-4-0,062, 2 слоя 0,124 0,3 Стеклотекстолит СТФ-1-18-0,25 0,25 0,3 Стеклоткань СТП-4-0,062, 2 слоя 0,124 0,3 3 18 Стеклотекстолит СТФ-1-18-0,15 0,15 0,3 Стеклоткань СТП-4-0,062, 2 слоя 0,124 0,3 2 18 Стеклотекстолит СТФ-1-18-0,15 0,15 0,3 Эласил 137-182 0,3 1,6 1 38 Стеклоткань СТП-4-0,062, 3 слоя 0,186 0,3 Клей ВК-9 с нитридом бора 0,3 0,9 4 (8-слойная) 8 38 DE104ML 0,100 B H000/H018 0,1 0,3 Стеклоткань СТП-4-0,062, 2 слоя 0,124 0,3 7 18 DE104ML 0,300 B H018/H018 0,3 0,3 Стеклоткань СТП-4-0,062, 2 слоя 0,124 0,3 6 18 5 18 DE104ML 0,300 B H018/H018 0,3 0,3 Стеклоткань СТП-4-0,062, 2 слоя 0,124 0,3 4 18 3 18 DE104ML 0,300 B H018/H018 0,3 0,3 Стеклоткань СТП-4-0,062, 2 слоя 0,124 0,3 2 18 DE104ML 0,100 B H000/H018 0,1 0,3 Эласил 137-182 0,3 1,6 1 38 Стеклоткань СТП-4-0,062, 2 слоя 0,124 0,3 Клей ВК-9 с нитридом бора 0,3 0,9 номера, действующие в рамках настоящей работы. Схемы, соответствующие тому или иному типу, представлены в табл. 1. В ней приведены марки материалов изоляционных слоев, значения их толщин и коэффициента теплопроводности. Напротив изоляционного слоя, в котором находится ПП, указана его суммарная толщина. Толщина слоя фольги определяется примененным фольгированным материалом, а толщина слоя гальванической меди принята равной 20 мкм. Это одно из самых

распространенных значений. Поскольку внешний ПП находится вне слоя изоляционного материала, то он записан отдельно в самой верхней строчке. Расположение слоев такое, что нижние слои – это материалы, через которые плата крепится к основанию. Вверху – внешний ПП (как на рис. 1 и 2).

Нумерация проводящих слоев – от основания. В качестве примера рассмотрим плату типа 2. Для этой платы n = 8, i меняется от 1 до 8. Номер для слоя материала СТФ-2-35-0,25 i = 6. Для прово-

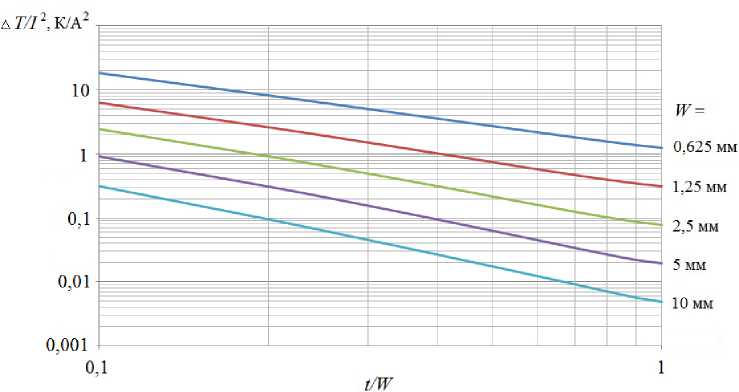
Рис. 4. Графики зависимости A T_n / 1 ² от t / W при разных W для внутреннего ПП ( j = 2) печатной платы типа 1 без гальванической меди

Fig. 4. Graphs of ATn /12 versus t / W at different W for the internal conductor (j = 2) of the type 1 printed circuit board without galvanic copper дящего слоя j = 3 (это один из проводящих слоев упомянутого материала) nj = 7. При этом nj -1 = 6, nj +1 = 8, а yminj равна сумме толщин слоев изоляционного материала с первого по шестой.

Из рис. 3 видно, что разница температур в объеме ПП незначительна по сравнению с разницей температур в объеме изоляционных материалов. Кроме того, это отмечено и в [6; 7]. Это связано с тем, что коэффициент теплопроводности материала ПП, как уже было отмечено раньше, значительно больше коэффициентов теплопроводности изоляционных материалов. Это позволяет сделать допущение, что поверхность ПП является изотермической. При расчете предполагалось, что температура основания в зоне ПП одинаковая (по оси ОХ ). ПП слишком мал, чтобы попасть в ту часть основания, в которой температура сильно зависит от координат. Температура основания зависит, главным образом от тепловыделения электронной компонентной базы, расположенной на печатной плате [6; 7], а коэффициент теплопроводности основания тоже велик. Однако ПП может пересекать зоны с разными температурами основания (по оси OZ , которая на рисунках не показана, но направлена вдоль ПП). Это следует учитывать при расчете.

Итак, тепловое сопротивление между двумя изотермическими поверхностями может быть найдено по формуле l1

R-r = —, (18) T J X S ( l )’

где dl – элемент длины пути теплового потока; S ( l ) - аналитическое выражение изотермической поверхности; X - коэффициент теплопроводности; l ₁ и l ₂ – параметры, характеризующие положение изотермических поверхностей, между которыми определяется тепловое сопротивление (поверхность ПП и основания). Очевидно, что на S ( l ) будет влиять как геометрия изоляторов и клеев, так и ширина ПП.

Перегрев ПП относительно основания можно найти по формуле

A T_n j = R r P j = I j ² R j R r , (19) где P_j – мощность, рассеиваемая на ПП j -го проводящего слоя при протекании тока; R_j – электрическое сопротивление ПП j -го проводящего слоя.

Из (13) видно, что перегрев прямо пропорционален квадрату тока. Тогда расчет не нужно проводить на разных токах, достаточно провести при одном токе, затем найти соотношение A T_n j / 1 2 . Расчетным путем построим графики зависимости A T_n / 1 ² (здесь и далее индекс j опущен, так как графики строятся для конкретного слоя, дублировать номер слоя смысла не имеет) от соотношения t / W при разных W . По этим графикам на практике можно легко определить требуемое значение t при заданных прочих параметрах. При проведении расчетов примем удельное электрическое сопротивление материала ПП, равное 1,72 · 10 ^–8 Ом · м, согласно РД 50-708-91, а коэффициент теплопроводности – 390 Вт/м·К. На рис. 4 представлены графики зависимости A T_n / 1 ² от соотношения t / W при разных W для

Табл. 2. Значения A T_n / 1 ² в K/A², при разных t / W , при разных W для внутреннего ПП ( j = 2) печатной платы типа 1 без гальванической меди

Table 2. Values A T_n / 1 ² in K/A², at different t / W , for internal conductor ( j = 2)

of a type 1 printed circuit board without galvanic copper

W , мм	t / W
	1	0,9	0,8	0,7	0,6	0,5	0,4	0,3	0,2	0,1
0,625	1,25	1,37	1,56	1,81	2,17	2,70	3,54	5,01	8,11	1,82E+1
1,25	3,11E-1	3,45E-1	3,95E-1	4,69E-1	5,77E-1	7,43E-1	1,02	1,51	2,61	6,34
2,5	7,78E-2	8,66E-2	1,02E-1	1,25E-1	1,60E-1	2,17E-1	3,13E-1	4,95E-1	9,19E-1	2,45
5	1,95E-2	2,20E-2	2,67E-2	3,40E-2	4,52E-2	6,30E-2	9,41E-2	1,56E-1	3,10E-1	9,17E-1
10	4,87E-3	5,67E-3	7,07E-3	9,15E-3	1,23E-2	1,74E-2	2,64E-2	4,51E-2	9,41E-2	3,10E-1

Табл. 3. Значения A T_n / 1 ² в K/A² для разных ПП печатных плат разных типов

Table 3. Values A T_n / 1 ² in K/A² for different conductor of printed circuit boards of different types

Тип 1
W , мм	j = 2		j = 1
	t / W
	1	0,1	1	0,1
0,625	9,82E-1	1,61E+1	7,29E-1	1,07E+1
1,25	2,45E-1	5,56	1,82E-1	3,77
2,5	6,13E-2	2,09	4,55E-2	1,46
5	1,53E-2	7,63E-1	1,14E-2	5,46E-1
10	3,83E-3	2,54E-1	2,85E-3	1,84E-1
Тип 2
W , мм	j = 4		j = 3		j = 2		j = 1
	t / W
	1	0,1	1	0,1	1	0,1	1	0,1
0,625	3,58	4,52E+1	4,05	4,64E+1	2,86	3,44E+1	8,86E-1	9,65
1,25	8,94E-1	1,38E+1	1,01	1,34E+1	7,14E-1	1,03E+1	2,21E-1	2,75
2,5	2,24E-1	4,66	2,53E-1	4,41	1,79E-1	3,44	5,54E-2	8,91E-1
5	5,59E-2	1,72	6,33E-2	1,66	4,46E-2	1,26	1,38E-2	3,40E-1
10	1,40E-2	6,34E-1	1,58E-2	6,41E-1	1,12E-2	4,73E-1	3,46E-3	1,31E-1
Тип 3
W , мм	j = 6		j = 5		j = 4		j = 3
	t / W
	1	0,1	1	0,1	1	0,1	1	0,1
0,625	6,31	7,38E+1	1,46E+1	1,58E+2	1,23E+1	1,36E+2	7,11	8,36E+1
1,25	1,58	2,13E+1	3,65	4,34E+1	3,09	3,75E+1	1,78	2,44E+1
2,5	3,94E-1	6,71	9,11E-1	1,32E+1	7,72E-1	1,13E+1	4,45E-1	7,87
5	9,85E-2	2,37	2,28E-1	4,68	1,93E-1	3,97	1,11E-1	2,79
10	2,46E-2	8,92E-1	5,70E-2	1,84	4,82E-2	1,55	2,78E-2	1,04
W , мм	j = 2		j = 1
	t / W
	1	0,1	1	0,1
0,625	4,88	6,13E+1	1,29	1,41E+1
1,25	1,22	1,87E+1	3,24E-1	4,00
2,5	3,05E-1	6,21	8,09E-2	1,33
5	7,62E-2	2,20	2,02E-2	4,96E-1
10	1,91E-2	7,92E-1	5,06E-3	1,89E-1
Тип 4
W , мм	j = 8		j = 7		j = 6		j = 5
	t / W
	1	0,1	1	0,1	1	0,1	1	0,1
0,625	7,25	8,62E+1	1,35E+1	1,47E+2	1,09E+1	1,21E+2	1,00E+1	1,13E+2
1,25	1,81	2,51E+1	3,37	4,09E+1	2,72	3,39E+1	2,5	3,18E+1
2,5	4,53E-1	8,03	8,42E-1	1,27E+1	6,80E-1	1,04E+1	6,26E-1	9,84
5	1,13E-1	2,88	2,11E-1	4,62	1,70E-1	3,73	1,56E-1	3,51
10	2,83E-2	1,08	5,26E-2	1,81	4,25E-2	1,45	3,91E-2	1,36

Окончание табл. 3

End of table 3

W, мм j = 4 j = 3 j = 2 j = 1 t / W 1 0,1 1 0,1 1 0,1 1 0,1 0,625 7,42 8,68E+1 6,56 7,82E+1 3,96 5,21E+1 1,05 1,17E+1 1,25 1,86 2,53E+1 1,64 2,31E+1 9,91E-1 1,63E+1 2,64E-1 3,42 2,5 4,64E-1 8,13 4,10E-1 7,54 2,48E-1 5,51 6,59E-2 1,16 5 1,16E-1 2,91 1,02E-1 2,70 6,20E-2 1,96 1,65E-2 4,41E-1 10 2,90E-2 1,1 2,56E-2 1,01 1,55E-2 7,00E-1 4,12E-3 1,66E-1 внутреннего ПП печатной платы типа 1, но без гальванической меди. В табл. 2 представлены значения ATn J12, по которым построен этот график. Как видно из рис. 4, при логарифмическом масштабе графики представляют собой практически прямую линию. Это облегчает процесс построения подобных графиков. Достаточно только две точки, например при t / IV = 0,1 и при t / IV = 1. Так, в табл. 3 содержатся значения ATn /12 для разных ПП печатных плат разных типов (представленных в табл. 1). Ввиду ограниченности объема настоящей работы графики для этих типов печатных плат не приведены, но их легко построить по двум точкам в логарифмическом масштабе. Значения W привязаны к стандартным шагам координатной сетки.

Ширина изоляционных материалов печатной платы в рассматриваемом случае – математическая абстракция. На практике в качестве W может выступать расстояние до соседнего ПП или, скорее, до температурного поля, создаваемого соседним ПП. При этом теплообмен между ними должен отсутствовать на линии, отстоящей от края ПП на расстояние ( I V - t ) / 2. Примером могут служить одинаковые ПП, с одинаковыми токами проходящие над зоной основания с постоянной температурой. В таком случае линия, на которой будет отсутствовать тепловой поток между ними, строго посередине. На этой линии температуры полей, создаваемых ПП, будут одинаковыми. Из-за этого и будут отсутствовать тепловые потоки. Чаще всего на практике координата точки t /2 не совпадает с координатой точки I V / 2 (несимметричная задача). В этом случае начало системы координат целесообразно расположить также посередине ПП. При этом за I V / 2 принять минимальное расстояние от края подложки до начала координат. При этом с противоположной стороны все, что больше I V / 2, будет отсечено. Таким образом, можно воспользоваться полученными в настоящей работе результатами. Реальная температура будет несколько меньше расчетной ввиду

влияния отсеченной части. Даже при этом расчетное значение будет ближе к реальному, чем по методике, приведенной в [6; 7].

Как и в печатных платах без металлического основания в рассматриваемых печатных платах температура зависит от W . В печатных платах без металлического основания при определенном соотношении t / I V температура стабилизируется. Дальнейшее повышение этого соотношения не ведет к снижению температуры. В ПП на металлическом основании решающую роль играют не только t , W , но и суммарная толщина слоев изоляционных материалов. Это связано с особенностями отведения тепла.

3. Описание методики

Для примера определим перегрев ПП второго проводящего слоя восьмислойной печатной платы типа 4. Графики зависимости A T_n / 1 ² от t / V при разных W для него представлены на рис. 5. Пусть V = 2,5 мм, I = 3,8 А, A T_n = 7 K. Соотношение A T_n / 1 ² ® 0,48 К/A ² . Откладываем значение 0,48 К/А ² на оси ординат. Проведем горизонтальную линию до пересечения с графиком, соответствующим V = 2,5 мм. Находим t / I V = 0,6 в точке пересечения. Находим t = 0,6 ■ 2,5 = 1,5 мм. Моделирование в ANSIS показывает, что при заданных значениях I , W и найденном значении t величина перегрева будет составлять 6,811 K. Если принять его за истинное значение, то относительная ошибка расчетов по температуре составит 2,8 %.

Рассмотрим второй пример для того же проводящего слоя той же платы. Пусть I V = 1 мм, I = 3 A, A T = 30 K. Соотношение A T_n / 1 ² « 3,3 К/A ² . Как видно из рис. 5, графика, соответствующего I V = 1 мм, нет. Его необходимо восстановить. Из рис. 4 и 5 видно, что при двукратном увеличении W расстояния между графиками по оси ординат при конкретном значении t / I V примерно одинаковые. Это можно использовать при восстановлении недостающих графиков. Рассматри-

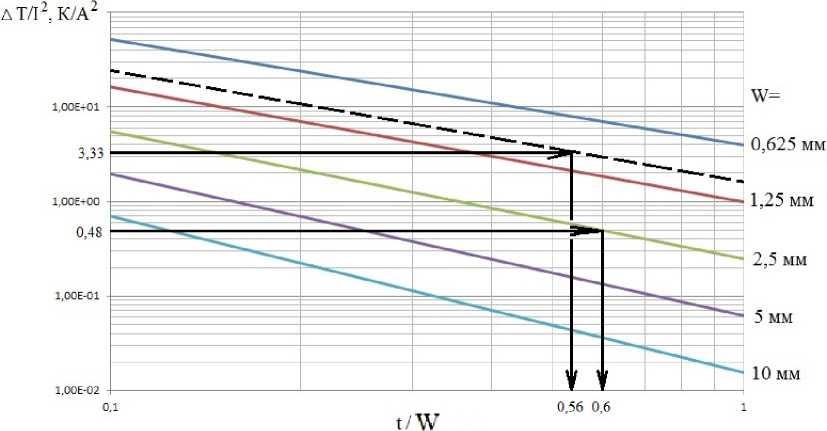
Рис. 5. Графики зависимости A T_n / 1 ² от t / W при разных W для ПП второго проводящего слоя ( j = 2) восьмислойной печатной платы типа 4

Fig. 5. Graphs of ATn /12 versus t / W, at different W for the conductor of second conductive layer (j = 2) eight-layer type 4 printed circuit board вать как логарифмическую шкалу с основанием 2. Восстанавливаем, таким образом, график для W = 1 мм (на рис. 5 показан пунктирной линией). Далее поступаем аналогично предыдущему примеру и находим t / W = 0,56. Тогда t = 0,56 мм. Моделирование в ANSIS показывает, что при заданных значениях I, W и найденном значении t величина перегрева будет составлять 26,776 К. Если принять его за истинное значение, то относительная ошибка расчетов по температуре составит 12 %.

Как видно из примеров, в случае отсутствия графика, соответствующего необходимому значению W , задача решается, но ошибка при этом существенно возрастает. Для ее снижения необходимо построить больше графиков. Это более ресурсоемкая работа. В целом полученная ошибка для технических расчетов вполне приемлема.

Для повышения точности вычислений графическим методом в логарифмическом масштабе текущее значение величины целесообразно определять по формуле

L

A = A I A max I L max , (20) min I I ,

I A min )

где A _min – минимальное значение величины на оси графика; A _max – максимальное значение величины на оси графика; L – расстояние от точки, соответствующей A _min , до точки, соответствующей текущему значению величины A ; L _max – расстояние от точки, соответствующей A _min , до точки, соответствующей A _max . L и L _max измеряются на

графике при помощи линейки или другого измерительного инструмента.

Чтобы отложить значение на оси, необходимо применить формулу, обратную формуле (20):

A

L = L max log,                                ⁽²¹⁾

min

A min

Заключение

Таким образом, была получена уточненная методика. К недостаткам полученной методики (правила выбора ширины по графикам и определение W в реальных печатных платах) можно отнести не только ее неуниверсальность, привязку к конкретному типу ПП, но и некоторую сложность применения к реальным печатным платам. Она сложнее, чем методика, приведенная в [6; 7]. Приведенную в настоящей работе методику целесообразно использовать в случае необходимости. Эта необходимость может наступить при особо плотной трассировке, когда ширина ПП имеет крайне важное значение. Если t / W близко к 0,1, что чаще всего целесообразнее просто заложить избыточную ширину ПП, выбрав его по более простой методике [6; 7]. Исключение составляет случай, когда в зоне W есть ПП, не выделяющие тепла (слишком маленький ток и печатная плата практически не нагревается, или они не работают одновременно с рассматриваемым ПП). Тогда увеличение t невозможно, поэтому целесообразно использовать методику, приведенную в настоящей работе.

Таким образом, в процессе работы были решены все поставленные задачи, а цель достигнута.