Уточнение методов расчёта вибрации шпиндельных бабок фрезерных и сверлильных деревообрабатывающих станков

Введение. Конструктивные особенности данного типа станков, заключающиеся в отсутствии зубчатых колёс в приводе, высокие частоты вращения шпинделей, многообразие типов фрез позволяют предположить, что в формировании спектров шума доминируют шпиндельная группа и режущий инструмент. Поэтому в качестве моделей акустических излучателей приняты:

е линейный источник (при R > 344/ f_k ), уровни звукового давления которого на основании данных [1, 2] для рассматриваемых станков приведены к следующему виду:

£ = 20 Igi^ + 20 lg f_k + 20lg / +10Ig R - 20 Ig r +124;

eточечный источник (при R <3^/fk ), звуковое давление которого приведено к следую щему виду

L = 201д^ +201д/^ + 201д/?/ — 201д г +106, где vk — скорость колебаний источника; fk — собственные частоты колебаний источника; R — радиус шпинделя или фрезы; / —длина источника; г— расстояние от источника до расчётной точки

Результаты исследований. Как видно из полученных зависимостей для расчёта уровней звукового давления следует определить собственные частоты колебаний и виброскорости на этих ча- стотах. Для этого в работе, в отличие от существующих, рассмотрены три варианта, приведённые на рис. 1

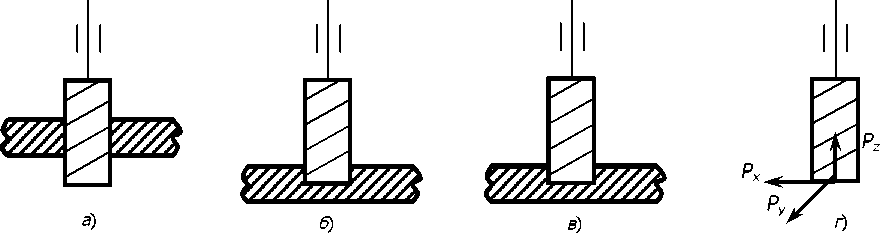
Рис. 1. Расчётная схема определения виброскоростей системы «шпиндельный узел — инструмент» деревообрабатывающих станков: а — отрезание или обработка торца изделия; б — фрезерование паза; в — схема, учитывающая весь шпиндельный узел; г — упрощённая схема фрез малого диаметра

Определение собственных частот колебаний и скоростей колебаний основано на использовании дифференцированных уравнений изгибных колебаний систем с распределёнными параметрами и функций А. К. Крылова.

Общее дифференциальное уравнение изгибных колебаний имеет вид:

Э

Эх2

э

Эх2

d2z

Эх2

Э2у

Эх2

d2z п

'°^=0

d2z п

+m-^°-

где Е — модуль упругости, Па; J — момент инерции в направлении соответствующей оси, м⁴; /ль — распределённая масса, кг/м.

Решение уравнения, соответствующее характеру возбуждающей силы, которая фактически является функцией периодического характера, определяется из уравнения:

Эх*

Э*у(х) 4 / \ п тождественного выражению свободных колебаний при значении

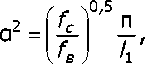
где f_c— собственные частоты колебаний, Гц; f_B — частота силового воздействия, Гц.

Первая схема. Решения уравнения (1) на участках фрезы, свободных от нагрузки, представим в виде [3]:

z(x) = Ak_t (ax) + Вк₂ (ax) + Ск₃ (ax) + Dk₄ (ох),                         (2)

где ^(ax^Kchax-b cosax ), £2(ax) = |(shax + sinax); £3(ax) = |(chax + cosax)

£4(ax) = |(shax + sinax).

Постоянные интегрирования определим из граничных условий. В точке приложения нагрузки должны выполняться условия сопряжения, требующие равенства прогибов, углов поворота и изгибающих моментов для обоих участков фрезы, а также скачка поперечной силы, равного по величине возмущающей силе. Поэтому

z(x) =z(x)  +^—к4[а(х -

\ /лев \ /прав "EJ V /J Располагая начало координат на правой опоре, получим

Z(х)   = Вк. (ax) + Dk. (ах), так как постоянные А и С равны нулю в соответствии с граничными условиями на правой опоре. Соответственно на левом участке амплитудные значения смещений выражаются формулой

z(xL_es = Bk₂(axV DkJax\+ -^— /cja(x - /?)] = 0. X /ЛСВ         X /      “ х /            “Lx      /J

О EJ

Постоянные В и D определим из граничных условий на левой опоре

^W) _{= a}2 dx²

Bk₄(afV Dk₂(afV           - ^)] = 0.

a EJ

Из системы (3) определяем

□ _ ^pz f к^У -5(Ж₄(а/)- /с₂[о(/ -Sf)]/c₂(a/) ^(a/) _ /с₄[а(/ -Sf)J ] a³E7[          /c₄(a/)-/c₂(a/)            k^ai) кг^^ /'

_D P_z /r₄[a(/-S*(a/)-/r₂[a(/-S*₂(a/) a³EJ        k^l>-k^l>        "

Тогда величина прогиба по оси OZ равна

z(x,t ) = [^(0%)+ D/c₄(ox)]p(z)l

Аналогичным образом находится прогиб и по оси OY.

v                        v CZ Sv

Радиальная скорость колебании определяется формулой — и —. Qt Qt

Собственные частоты колебаний заготовки определяются по известной формуле

_ п2/?2 ( И

° ” 2/2 |/770

10,5

| (л = 1,2,3,-..)

Полученные выше зависимости справедливы для абсолютно жёстких опор. Фактически передний подшипник шпинделя с патроном и обрабатываемая заготовка являются упругодиссипативными опорами, податливость которых существенно влияет на динамические параметры системы «шпиндель — заготовка».

Вторая схема. Рассмотрим теперь фрезу, опёртую по концам на две упругие опоры с коэффициентами податливости ci (заднего центра) и с₂ (переднего шпиндельного подшипника и зажимного устройства). Начало координат расположим на заднем центре. Граничные условия на концах заготовки запишем в виде:

d²y(d)^ = 0 d²y/dx^L = 0,

х = 0 у = Qcy, х=! y=Qcy, где Q — амплитудное значение поперечной силы в соответствующем сечении, определяемой по формуле d3v Q = D^-dx5

С учётом последнего выражения получим граничные условия в следующем виде d3y dx3

= 0

х=0

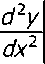
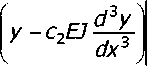
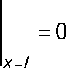
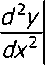
Подставляя в эти уравнения общее выражение для прогибов (2) и учитывая соотношения функций А. К. Крылова, получим следующую систему уравнений относительно постоянных А В, С, D

A + c1Eb3D = 0,

А [^ (А) - c^EJa3^ (А)] + В |>2 (А) - с2Е7о3^3 (А)] + D [^ (А) - с2£7о3^ (А)] = О, Ak3 (А)+Вк. (А)+Ок2 (А) = О, где А = а/.

Решая данную систему, получим выражение для определения собственных частот колебаний

(shA - sinA)² -c^EJa³ (chA + cosA) (shA - sinA) - chA-cosA -с₂£7а³ (shA + sinA) c^Ja³ (shA -sinA) -

-(shA + sinA - c^EJa³ (chA + cosA)] (shA + sinA - c^EJa³ (chA - cosA)] = 0.

Представляя нагрузку с помощью дельта-функции и учитывая краевые условия (4), получим дифференциальное уравнение поперечных колебаний заготовки на податливых опорах

Э²у ₂9⁴У --— -|- Q^Z --— 5f² dx⁴

n=lL

. Зплх

-sin—-—

. сэРэ -cR. „ c,R, „   „ где А = 2 2 ——; В = -^; А и R2 — реакции в опорах заднего центра и в переднем шпин-/2                   / дельном подшипнике.

Аналогичным уравнением описываются колебания по оси ус учётом замены Р_у и /^на P_z^и P_z-

Эти уравнения в конечном виде не интегрируются, поэтому для их решения использованы численные методы.

В качестве начальных условий принимаем (х = / и t =0)

У = c_zP_y и dy/dt = d{c₂R₂)/dt, где R₂ — реакция в переднем шпиндельном подшипнике.

Решение этой задачи с использованием функций А. К. Крылова имеет вид

Р

У лев = "РуСук_х (ах) + Вк, (ах) + Ок. (ах) + -^ к. [а (/ - St)].

Постоянные В и О определим, исходя из краевых условий на левом конце заготовки, получаем систему уравнений:

из которой вычисляем

D =

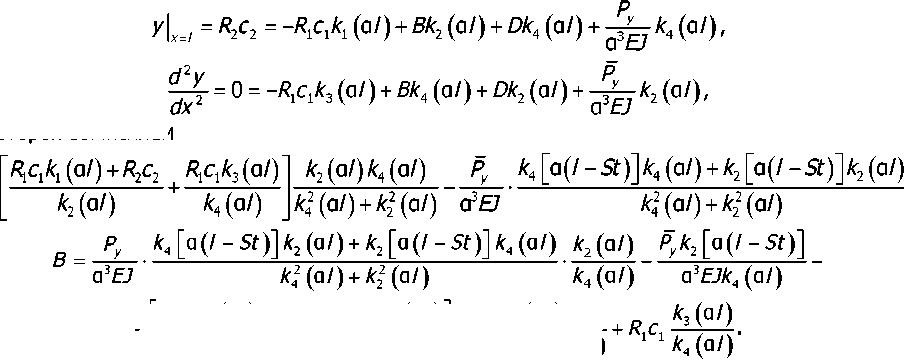
/?1с1А1 (a/) + R2c2 R^^ (а/)	А2(а/)
_     А2(а/)      ' А4(а/)	А2(а/) + А2 (а/)

Вибросмещения по оси у в этом случае определяются выражением у (х, t) = [- RiC^ (ox)+Bk2 (ox)+Dk^ (ox)](l+C*si noot)

Теперь определим радиальную скорость колебании как —. Аналогичными выражениями описы-6t ваются Ах. t) и —с учетом замены Pv и Pv на Р7 и ' • '                    '                          у У Z Z

В окончательном виде прогибы режущего инструмента по оси z определяются выражением z(x) = ^A(chax + cosax) + В (shax + sinax) + /?(shax -sinax)] sincot.

Прогибы режущего инструмента по оси OY находятся по аналогичному выражению, в котором сила /^заменяется на Р_у.

Третья схема. Для существенного уточнения колебательной модели следует рассмотреть систему шпиндель — заготовка, которая представляет собой балку на двух опорах с консольной частью. В данной расчётной схеме приняты следующие обозначения: Л— средневзвешенный момент инерции межопорной части шпинделя, а Л — средневзвешенный момент инерции консольной части.

Для каждого из участков запишем выражения прогибов, используя функции А. К. Крылова: У1 = с₁/с₁(Лх)+с₂/с₂(Лх)+с₃/с₃(Лх)+с₄/с₄(Лх) при о <  х < Ь, у₂ = c^^Qo^ c'₂k₂Qo<^+Сзк₃(>о<^+с^ при ь < х < /, где /—длина шпинделя и заготовки, м; Ь — длина межопорной части шпинделя, м.

На первом участке у^ = у₂(о) = 0

Поэтому q = с3 = 0

В точке сопряжения двух участков

5У1 Qx

_ 9Уг дх

уМ = уМ

Поперечные силы в конце первого и начале реакции.

Поэтому

второго участка отличаются на величину опорной

9^1

Эх3

9^2

Эх3

-R.

Условия сопряжения участков можно выполнить, если представить прогибы на втором участке в виде

ЗгУг = ЛУ1 +-^^[ь(* -£)1 Л Е

Функция А4В выражении (6) тождественно равна 0 при х<Ь и не равна 0 при х>Ь. Последнее выражение справедливо для всей системы «шпиндель — заготовка». Подставив в (5) выражение для yi получим (Ci = с₃ = 0)

У = + где А =

Полученное выражение для /содержит постоянные с2, с^ и R, которые можно определить из условий х = b

У = 0

У = У = 0.

В итоге получаем систему из трёх уравнений c₂k₂^\b^+c_Ak^b^ = О,

^k^lVM^V^kM - ^)] = 0,           (7)

-Д)] = 0.

Приравнивая нулю определитель системы (7), получим уравнение для расчёта собственных частот колебаний:

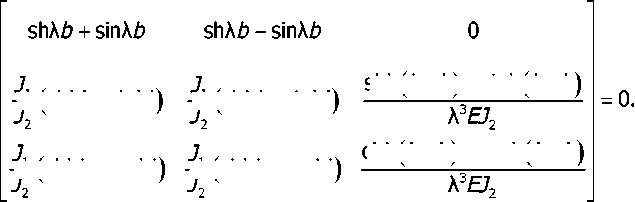
—(shA/ -sinA/)

—(shA/ + sinA/)

shA(/ -d) + sinA(/ -b)

—(chA/ -cosA/)

—(chA/ + cosA/)

chA(/ -b) + cosX(l -b)

Четвёртая схема. Координата приложения нагрузки на фрезе не меняется относительно точки закрепления. Расчётной моделью является консольно-защемлённая балка. Прогибы фрезы по осям 03л ОКопределяются из уравнения (1), в котором

,2

2л-1

2/P J

₂ wn^{2 Q}

'pi I

Здесь ^/—собственные частоты колебаний фрезы, Гц; /р —длина консольной части, м.

Для функции z(x)=/^(ax^S/^ax^C/^ax^D/c^ax) имеем граничные условия р Р х = 0 z(x) = ^; z(x) = 0, v ’ ЗВ v ’

, р

При z(x = 0) = 0 получаем, что С= 0, а

Р I3

p

Из остальных граничных условий находим:

-Л/г1(а/р)+^2(а/р)+/?/г4(а/р)= 0

- ,U₃ (о/р)+ Вк_А (о/р)+ Ок₂ (а/_р ) = 0 После преобразований получаем

P_ZP_D cho/_Dsino/_D -sho/_Dcoso/_D

6В_р sho/pSino/p

P_zl³ cha/„sino/„ + sha/„cosa/„ p _ ^z p __p_____p_______p_____ p

6Е7р

sho/pSino/p

Выводы. Приведённые результаты исследований позволяют существенно уточнить модели виброакустической динамики основной колебательной системы «шпиндельный узел — режущий инструмент» модельных и сверлильных деревообрабатывающих станков. Обоснован общий подход к расчёту процесса шумообразования этих станков. Различия в самом расчёте заключаются только в задании силового воздействия от процесса резания. Полученные зависимости учитывают все основные конструктивные параметры как режущего инструмента, так и шпинделя, а также параметры технологического процесса.