Уточнение обобщенной математической модели системы твердых тел, прикрепленных к балке Эйлера — Бернулли

При моделировании механических систем, состоящих из упругих балок и взаимосвязанных твёрдых тел, возникают значительные трудности, обусловленные сочетанием сосредоточенных и распределённых параметров. Для корректного описания динамики таких систем возможно применение вариационного принципа Гамильтона — Остроградского. Результатом анализа полученных уравнений, описывающих движения различных механических систем, является обобщенная математическая модель для класса механических систем с расчетной схемой «тело (система тел) на балке Эйлера — Бернулли» [1-3] и выглядит следующим образом:

Aq + Cq + C ( Dq - u ) = 0,

²M             4'11          m                                            ⁽¹⁾

a Z-U ( x , t ) + c ' u ( x , t ) = X k i ( d^q ( t ) - u ( x , t )) d ( x - a j,

I d t              d x           i = 1

где x — переменная по оси координат, совмещенной с покоящейся балкой; q(t) — n-мерная вектор-функция, характеризующая положение системы твердых тел;

u ( x , t ) — скалярная функция поперечных прогибов стержня, удовлетворяющая граничным условиям, определяемым типами закрепления его концов;

a i , ( i = 1, m ) — точки крепления пружин к балке, причем 0 <  a i <  l ;

u ( t ) — вектор-функция составленная из u ( a 1 , t ),..., u ( a m , t );

• A , C — матрицы n x n ;

• C — матрица n x m ;

• D — матрица m x n ;

• d‘ — вектор, состоящий из строк матрицы D ;

• a = p F — погонная масса стержня;

• c = EI — изгибная жесткость балки;

• k i , ( i = 1, m ) — упругость пружин.

Система (1) представляет собой гибридную систему дифференциальных уравнений (ГСДУ) из обыкновенных дифференциальных уравнений и уравнений в частных производных. Гибридные системы подобного типа изучены недостаточно, и для их решения требуется разработка специализированных методов. Одним из таких методов является подход к исследованию свободных колебаний, описанный в работе [2].

Настоящая работа является обобщением ранее полученных результатов. Выполнено уточнение обобщённой математической модели в выбранной системе координат: в отличие от ранее рассматривавшийся гибридной системы дифференциальных уравнений уточненная модель включает неоднородные слагаемые в правой части, что позволяет более полно учитывать физические особенности системы.

Дополнительно предложен метод сведения уточнённой модели к ранее изученной задаче посредством подходящей замены переменных. Такая редукция обеспечивает применимость разработанных ранее аналитикочисленных методов исследования свободных колебаний, основанных на аппарате обобщённых функций [2; 4].

Построение решения опирается на метод определения положения равновесия системы, описанный в работе [5].

Таким образом, расширение класса рассматриваемых задач достигается за счёт одновременного уточнения модели и сведения её к известной постановке, что открывает возможность использования уже апробированных математических инструментов для анализа динамики системы.

• 1    Обсуждение к уточнению обобщенной математической модели

Ранее при выводе обобщённой математической модели (1) рассматривался упрощённый случай с фиксированными либо симметричными точками креплений пружин относительно центров масс твёрдых тел.

При произвольных точках крепления обобщенная математическая модель в выбранной системе координат в отличие от рассматриваемой ранее (1) будет содержать неоднородности в правой части. Откуда и возникает необходимость уточнения обобщенной математической модели.

Действительно. Рассмотрим применение вариационного принципа Гамильтона — Остроградского на примере механической системы (рис. 1).

Oxz — система координат, центр которой совпадает с точкой закрепления стрежня, а ось Ox направлена вдоль оси стержня.

O ‘ x ‘z' — подвижная система координат, связанная с твердым телом.

Состояние равновесия такой системы характеризуется параллельностью осей координат Oxz и О' x ' z ' .

Твердое тело может совершать поступательные движения вдоль оси Oz и совершать угловые колебания ^ . Перемещение точек стержня в направлении оси Oz описывается функцией u ( x )

z

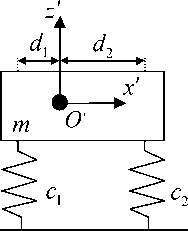
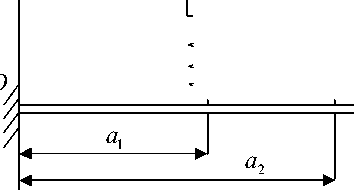
Рис. 1. Механическая система

«твердое тело, прикрепленное с помощью двух пружин к стержню»: m — твердое тело массой m ; a 1 и a ₂ — точки крепления пружины к упругой балке;

C j и c ₂ — упругая пружина; d 1 и d ₂ — расстояние точек крепления пружин относительно центра подвижной системы координат 0 ' x’z’ ; l — длина упругого стержня

Ф

l

x >

Продемонстрируем вывод математической модели динамики системы. Данная система содержит как сосредоточенные и распределенные параметры. Так как рассматривается модель консервативной механической системы, то вариация функционала действия по Гамильтону будет иметь вид:

t 1

8J = 8 J (T - U) dt = 0,

t 0

где T и U являются кинетической и потенциальной энергией системы и будут иметь следующий вид:

T = T + Т , U = U + U

тела стержня ,            пружин стержня

Кинетическая энергия тела Tтела состоит суммы кинетической энергии поступательного и вращательного движений:

.7 Т ' 2

,

• ¹    тела 2       2

где 1р — момент инерции твердого тела относительно центра масс при повороте на угол (р .

С учетом того, что движение тела по оси Ox отсутствует, а угол поворота р полагается малым, потенциальная энергия пружин будет иметь следующий вид:

U = С 1 ( z + z ‘ - d 1 ^ - U ( a i , t ))²

1                    2

c ₂( z + z ‘ + dxp - u ( a ₂, t ))²

⁺           2

где x ‘ , z ‘ — координаты точек крепления пружин к телe в системе координат О'x'z' ;

• x , z — перемещение в неподвижной системе координат Oxz .

Потенциальная и кинетическая энергии стержня имеют вид:

Tcmep_ = тpF l^u I dx, Ucmep_= E^dU dx ,(6)

с^тер^жня                                      с^тер^жня2

• 2o    /d t 2                  2o

где p F — погонная масса стержня, EI — изгибная жесткость балки.

Полное описание математической модели (рис. 1) с применением вариационного принципа Гамильтона — Остроградского изложено в работе [2] и имеет вид следующей ГСДУ:

mz_o + c 1 [ z ₀ + z ‘ — d 1 ф - u ( a 1 , t ) ] + c ₂ [ z ₀ + z ‘ + d₂ p - u ( a ₂, t ) ] = 0,

I _v$ - c d 1 [ z ₀ + z [- d 1 ф - u ( a 1 , t ) ] + c ₂ d ₂ [ z ₀ + z ‘ + d₂ p - u ( a ₂, t ) ] = 0,

[ z ₀ + z ‘ - d 1 ф - u ( x , t ) ] § ( x - a 1 ) +

d2 u      54u pF + EI = ci dt      dx

+ c ₂ [ z ₀ + z ‘ + d₂ p - u ( x , t) ] § ( x - a ₂ ) .

Для наглядности перепишем (7) в виде:

mz₀ + c [ z ₀ - d 1 ^ - u ( a 1 , t ) ] + c ₂ [ z ₀ + d ₂ (p - u ( a ₂, t ) ] = - cz ’- c ₂ z 2 ,

Ip p - cd 1 [ z ₀ - d p p - u ( a 1 , t ) ] + c ₂ d ₂ [ z ₀ + d₂ p - u ( a ₂, t ) ] = cd 1 z ‘ - c ₂ d ₂ z 2 ,

[ z ₀ + z ‘ - d 1 ^ - u ( x , t ) ] S ( x - a 1 ) +

d2 u dr8 4 u pF + EI= ci dt      dx

+ c ₂ [ z ₀ + z ‘ + d₂ ^ - u ( x , t) ] S ( x - a ₂ ) .

В правой части системы (8) имеем неоднородность, которая не позволяет использовать разработанные аналитико-численные методы исследования свободных колебаний [2; 3].

Замечание. В случае, когда что точки крепления упругих элементов равноудалены от центра масс твердого тела, то есть z‘= z‘= z,                                       (9)

то неоднородности в ГСДУ (8) будут сокращаться, и она принимает вид обобщенной математической модели (1) с следующими коэффициентами:

q =

z 0 + z

V ^ )

( u ( a ₁, t )

V u ( a 2 , t ) )

a = p F , c = EI , k 1 = c ₁, k ₂ = c ₂,

( m 0

I 0 I, )

d1 =

1 Л

V d 1)

d2

(0   0^

C =

10 0)

(1Л

C =

V- c i d i

c ₂ d ₂ )

D =

— d 1

V1

^d 2 )

2 Уточненная обобщенная математическая модель

Запишем неоднородности, зависящие от места расположения крепления жестких пружин, полученные в выражении (9) как n -мерный вектор b .

Тогда уточненная обобщенная математическая модель примет вид:

Aq + Cq + C ( Dq — u ) = b ,

m

— u (x, t ))8( x — ai) + ^ Pi8( x — ai), i=1

d u        d u      -m att(x,t)+ctt(x,t)=Xki(d q(t)

О t              О X            i = 1

где P i , ( i = 1,2,..., m ) — заданные числа.

Для приведения уточнённой модели к виду (1) предлагается воспользоваться подходом к нахождению положения равновесия системы, описанным в работе [5].

Предположим, что n -мерный вектор q и скалярная функция V(x) не зависят от времени t и являются решениями системы (10). При этом будут выполняться следующие условия:

q (0) = q , u ( x ,0) = V ( x ), 0 <  x <  l .

Тогда подставив их в (11), получим

'( C + CD ) q — CV = b ,

= d4V cтг(x)=£(ki(d q—V(x)+P)5(x—ai)’ dx           i=1                                1

где V — вектор составленных скалярных функций V ( a ₁), V ( a ₂), _ , V ( a m ).

Запишем краевые условия для функции V(x), соответствующие типу крепления стержня:

/ 1 ( V (0)) = 0,       Y 2 ( V ( l )) = 0.                         (13)

И тогда для системы вида (12) с краевыми условиями (13) справедлива следующая теорема, с подробным доказательством которой можно ознакомиться в работе [5].

Теорема 1. При любых значениях q для обобщенного решения V ( x ) дифференциального уравнения системы (12), удовлетворяющего краевым условиям (13), справедливо представление

m

• V(x) = Ent(x-ai)(ki(d-Tq - V(ai) + P),(14)

i = 1

где функции n i (x ), ( ' = 1,..., m ) — обобщенные решения уравнения

4m c in (x) = X 5( x),(15)

dx удовлетворяющие краевым условиям yM-ai)) = 0,     Y2(ni(l- ai) = 0.

Воспользуемся теоремой 1. Подставим в соотношение (14) x = a i ,

( i = 1,2,..., m ) , п олучим систему уравнений относительно q , V :

Nq - MV = b1(17)

где M — матрица m x m :

^ 1 + П1(0) к 1    П 2( a1 - a 2) k2Vm (a1 - am ) km"

J1( am - a1) k 1  П 2( am - a 2) k2.............1 + Um (0) km7

N — матрица m x n :

(

En(a1- a) Pi i=1

m b1 =

E^ta2 - ai)Pi i=1

E n i ⁽ a m ^- a i )P i x i = 1                     7

Теперь запишем систему линейных алгебраических уравнений относительно q , V с учетом алгебраической части системы (12).

( C + CD ) q - CV = b , Nq - MV = b₁.

Из полученной системы (18) мы можем найти значения векторов q и V , которые определяют положение равновесия системы (10). Для этого требуется найти функции n i (x ), ( i = 1,..., m ), являющиеся обобщенными решениями уравнения (15). C подробным описанием нахождения функций n i (x )можно ознакомиться в работе [5].

Заключение

При моделировании более широкого класса задач, учитывающих несимметричное расположение точек крепления пружин к твёрдым телам, возникает необходимость в уточнении ранее разработанной обобщённой математической модели системы взаимосвязанных твёрдых тел, соединённых с балкой Эйлера — Бернулли посредством упругих элементов. Несимметрия приводит к появлению неоднородностей в правой части уравнений, что обусловливает переход к рассмотрению гибридной системы дифференциальных уравнений (ГСДУ) вида (10).

Для ГСДУ (10) найденные положения равновесия q и V ( x ) в выбранной системе координат дают возможность перейти к новым переменным посредству замены:

q (t) = q (t) + q, u (x, t) = U( x, t) + V (x), что позволяет свести задачу к уже исследованной ранее обобщённой математической модели [1]. При этом переменные q%(t) u%(x,t) можно интерпретировать как переменные, описывающие колебания механической системы относительно положение равновесия.