Уточнение расчетных зависимостей несущей способности металлокомпозитных оболочек, работающих на устойчивость

В статье автора [1] охарактеризована методика сопоставления и согласования расчетных и экспериментальных значений несущей способности слоистых оболочек, работающих на устойчивость. Напомним вкратце сущность разработанной методики.

Основываясь на проведенных ранее исследованиях [2], заметим, что величина критической нагрузки будет зависеть от комплекса структурных и геометрических параметров: числа слоев в пакете N, толщины слоя h, угла укладки слоя а, соотношения слоев ф, уложенных под различными углами, последовательности укладки слоев в пакете, коэффициента армирования слоя ф, безразмерных параметров L и H (L- длина, R - радиус, H - толщина пакета оболочки), а так- же от упругих характеристик исходных компонентов, составляющих однонаправленный слой композиционного материала. В связи с этим, очевидно, в зависимости от комплекса этих параметров будет изменяться также и функция согласия экспериментальных и расчетных данных.

Следовательно, каждому комплексу геометрических и структурных параметров оболочки соответствует определенное значение критической нагрузки.

Это говорит о том, что критическая нагрузка оболочки, спроектированная из однонаправленных слоев в пакете, может описываться функцией от целого ряда параметров геометрического и структурного характера:

q = F I L ; H: N ; ^ ^; v ; а П; E a ; E c ; ^v a ; ^v c ; G a ; G c V R R

где П – вариант порядка расположения слоев в пакете.

В многомерном пространстве геометрических, структурных и упругих параметров в логарифмических координатах критическую нагрузку можно представить в виде гиперплоскости.

lg q = ^a i • lg L + a 2 • lg H + ... + a k lg G c + C i .

RR

Уравнение (2) удобно представить в виде: k

Z ' = Ya ‘• Xj + C ‘ .

jj j=1

Поскольку теоретические значения критической нагрузки представляют собой гиперплоскость, то, следовательно, и экспериментальные значения должны с некоторым отклонением также аппроксимироваться уравнением гиперплоскости. Поэтому, используя методы аналитической геометрии, мы можем найти корректирующую функцию для расчетных значений.

Строго говоря, использование уравнения (2) наиболее эффективно в том случае, когда есть уверенность, что критическая нагрузка имеет экспоненциальную зависимость от входящих параметров или близкую к ней. В случае если это не имеет места, то результаты согласования могут быть менее эффективны. Как показано в классической литературе [3], поведение критической нагрузки в зависимости от геометрических параметров L и H имеет экспоненциальный харак-RR тер. Следовательно, в нашем случае данный подход является приемлемым и обоснованным.

Допустим, экспериментальные значения критических нагрузок аппроксимируются следую- щим уравнением гиперплоскости: k

Z" = Ta a"• Xj + C".(4)

j = i

Тогда, вычитая из (4) уравнение (3), мы получим значение корректирующей функции: k

Z''- Z' = Taj • Xj + C.(5)

j = i

Действительно, обозначив правую часть уравнения (5) lg K , будем иметь:

Z'- Z = lg K.(6)

Подставив в левую часть уравнения (6) истинные значения, будем иметь:

^

lg q э - lg q р = lg K = lg — .(7)

V ^q р )

И окончательно будем иметь:

q э = Kq р.

Отсюда, зная K , мы можем корректировать расчетные значения критических нагрузок, согласовывая их с экспериментальными данными.

Перепишем уравнение (5): k

Z = T a j • X j + C .                                                                (9)

j = i

Найдем методом наименьших квадратов уравнение гиперплоскости корректирующей функции. Используя методы, предложенные в работе [4], запишем систему, определяющую коэффициенты a_j , C по экспериментальным данным:

Расчет и конструирование

где L =	l 11 l 12 ... l 1 k l 21 l 22 ... l 2 k	; Lj =	l 11 l 12 ... l 10 ... l 1 k l 21 l 22 ... l 20 ... l 2 k	; L c =	l ll l l2 ... l l. k - 1 ... l l0 l 2l l 22 ... 1 2. k - l— l 20
	lk 1 lk 2 ... lkk		lk 1 lk 2 ... lk 0 ... lkk		l k l l k 2 ... lk . k - l— lk 0

Элементы, входящие в определители L , L_j , L_c , определяются следующим образом:

n lrs = УлXS rs                ri si ni I

1 ⁿ l pk = ^_ Z ^X pi ;

n i I

- <  r <  5 <  p <  k ;

n lpo = - Z Zi* Xpr.

n i I

Скорректированная зависимость (8), отражающая влияние экспериментальных данных, позволяет определить разброс уточненной расчетной зависимости, который удобно определять через коэффициент K . Следует заметить, что разброс по коэффициенту K должен быть наименьшим, поскольку корректирующую функцию мы находим по методу наименьших квадратов.

Используя разработанную методику, проведем согласование теоретических расчетных значений имеющимся экспериментальным данным, взятым из работы [5] и представленным в таблице.

Кольцевая укладка у» 0,3.

Параметры оболочки

№ п/п	h , мм	N	L , мм	у	R H	L R	q э , МПа	q p , МПа	K	q * , МПа	K *	q к = ^Э- 1 q * p	( K l - K l ) 2
1	0,184	9	178	0,328	36,76	2,92	5,4	5,51	0,9800	5,454	0,9898	0,9901	0,001807
2	0,173	13	177	0,345	27,03	2,91	10,2	11,88	0,8586	9,730	0,8190	1,0483	0,000246
3	0,224	12	180	0,271	22,68	2,96	13,1	15,45	0,8479	12,788	0,8277	1,0244	0,000067
4	0,227	12	180	0,266	22,32	2,96	14,5	15,90	0,9119	13,046	0,8205	1,1114	0,006216
5	0,210	15	181	0,287	19,34	2,97	16,1	23,20	0,6939	17,978	0,7749	0,8955	0,018788
6	0,183	15	182	0,330	22,22	2,99	15,1	17,40	0,8678	15,168	0,8717	0,9955	0,001376
7	0,200	14	180	0,296	21,74	2,96	17,8	17,70	1,0056	14,316	0,8088	1,2434	0,044416
8	0,196	14	180	0,296	22,17	2,96	13,0	16,70	0,7784	13,652	0,8175	0,9522	0,006459

Для наглядности графического изображения корректирующую функцию представим зависимой только от геометрических безразмерных параметров _R ^L и ^H _R . В данном случае берем об-

RH ратную величину — = -/ — также из условия удобства изображения и наглядности. Поскольку HR перейти от одной величины к другой не представляет труда, то lg — = - lg — . HR

Представим корректирующую функцию в следующем виде:

lg K = a ⋅ lg _H ^R + b ⋅ lg _R ^L + C .                                                                 (13)

Применяя процедуру метода наименьших квадратов и используя данные таблицы из 8 оболочек кольцевой укладки пакета при коэффициенте армирования ψ= 0,3, найдем уравнение плоскости, которое будет отражать корректирующую функцию. Система уравнений (10), определяющая неизвестные коэффициенты a , b , С , будет иметь вид:

Χ i = lg ^{R i} ; Z i = lg K i ; Υ i = lg ^{L i} .

Hi                    Ri

Используя (14), (15) и (16), уравнение (13) будет иметь вид:

lg K ^* = 0,54648 ⋅ lg ^R + 6,24507 ⋅ lg ^L - 3,7662.

HR

Зависимость (17) удобнее представить в виде:

lg K^x = 0,54648 ⋅ lg ^R + 6,24507 ⋅ lg ^L - lg5837.

HR

a =	Δ a ; b = Δ	Δ b ; C = Δ ; C =	Δ c Δ ,	(14)
	Z X 2	ΥΧ	Z Xt		Z Z , X i Z Y i X i Z X ,
	n	n	n		nnn
где Δ=	Z X i Y i	Z Y 2	Z Y i	; Δ a =	Z ZY i Z Y i 2 Z Y i ;
	n	n	n		nnn
	Z X i	Z y	1		Z Z i   Z Y i    1
	n	n			nn
	Z X 2	ΖΧ	Zx.		Z X 2 Z Y i X i Z ZX
	n	n	n		nn  n
Δ b =	Z X,Y,	Z Z i Y i	Z Y i	; Δ c =	ΧΥ   Υ 2    ΖΥ ii i ii .                         (15)
	n	n	n		nn  n
	Z X i	Z z i	1		Z X i  Z Y i   Z Z i
	n	n			nn  n

В определителях (15) приняты следующие обозначения:

Отсюда:

0,54648

K * =—• I R I

5837 I H J

⋅

L x 6,24507

R J

.

С учетом (19) и теоретической расчетной зависимости, приведенной в работе [6], уравнение уточненной расчетной зависимости (8) будет иметь вид:

_R 0,54648

q_n = 1,713 - 10 4 • I — I р            I H J

⋅

L x 6,24507

R J

⋅

⋅ a 33 R X П (

-

^a 13 ^a 22 ^{+ a} 23 ^a 11 ^- 2 ^a 12 ^a 23 ^a 13

^a 11 ^a 22

-

2 ^a 12

.

На рисунке показана процедура корректировки расчетных значений, построенная по данным таблицы (точками показаны экспериментальные значения). По уточненной расчетной зависимости (20) рассчитан коэффициент K ₁ , значения которого показаны в двух последних колонках таблицы. Среднее его значение равно K 1 = 1, 03261 , а коэффициент вариации ν _k 1 = 0,103 .

Расчет и конструирование

Таким образом, разброс экспериментальных и расчетных значений по коэффициенту K составляет порядка 10,3 %.

Подобная величина разброса объясняется малым числом испытаний и сравнительно большим диапазоном значений коэффициента армирования ψ .

Корректирующая согласующая функция (19), строго говоря, соответствует лишь тем экспериментальным данным, которые представлены в таблице. К сожалению, экспериментальные точки по параметру L мало отличаются друг от друга, поэтому корректирующая функция (19), а следовательно, и уточненная расчетная зависимость (20), показанная на рисунке цифрой 2 в направлении L , отражает согласие, очевидно, только в этом малом диапазоне изменения этого параметра.

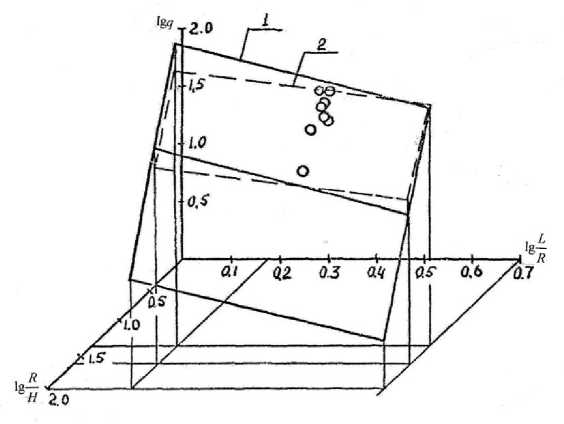
Сопоставление расчетных и экспериментальных значений критических нагрузок слоистых боралюминиевых оболочек при ψ = 0,3 и φ = 0: 1 – расчетная плоскость; 2 – уточненная по экспериментальным данным плоскость

Для более надежного экстраполирования необходимо получение экспериментальных значе-

L

. R

ний в более широком диапазоне изменения параметра

Таким образом, разработанная методика согласования расчетных и экспериментальных значений, основанная на представлении зависимости в виде гиперплоскости логарифмических величин входящих параметров, позволяет определять уточненную расчетную зависимость благодаря введению корректирующей функции, найденной методом наименьших квадратов.

Использование уточненной расчетной зависимости позволяет снижать статистические характеристики, определяющие разброс расчетных и экспериментальных значений по коэффициенту K , и тем самым более обоснованно подходить к назначению коэффициентов безопасности конструкций.