Уточнение расчетных значений осевых моментов инерции твердого тела на основе измерений параметров его динамической неуравновешенности

Величины осевых МИ пластинки удовлетворяют следующим соотношениям:

JX ⁼ J_х ~ Js ⁼ J X* d — J_s = J X + J_х + 2 Jyoz ~ Js ⁼ J X"V 1J yoz ;

J У — J у J_x — Jy"t (1 J_s — J у "V J у "V'XJ yOZ J^ — J V "^ 'U yOZ ,

Jz — J, — Js = Jz+ d — J$ — Jz^ J. + I. J yoz ~ Js = JZ'V'ZJyoz.

Здесь J_x,J_y,J_z - действительные МИ рассматриваемого твердого тела; J_x,Jy,Jz - так называемые «граничные» [1] МИ; J_s - осевой МИ шара с центром, совпадающим с началом координат (точкой О) и с центром пластинки; d > 0 - величина, на которую граничные МИ меньше действительных.

Из этих уравнений, учитывая, что Jy_0: ^ 0, видим, что МИ этой пластинки J_x, J_y, J _ больше или равны соответствующим граничным МИ. Равенство имеет место лишь при J _уог = 0, когда оси у и z перпендикулярны той главной оси инерции в точке О данного тела, МИ относительно которой максимален.

Для уточнения приближенных значений осевых моментов инерции твердого тела J'_x, J'_y,J'_:, полученных, например, расчетным путем, нам потребуется знание попарных разностей осевых МИ:

\_xy=J_x-J_y,\_y2=J_y-J_;^_2X=J_:-J_x,                                    (1)

которые могут быть определены по показаниям балансировочного станка после трёх вращений вокруг трёх различных осей. Условия на взаимное положение этих осей и формулы расчета попарных разностей Аху, А , А,х из показаний станка приведены в работе [2].

Иванов И.И., Тверской М.М. Уточнение расчетных значений осевых моментов инерции твердого тела...

При практических вычислениях удобнее выбрать направление оси п' противоположным принятому в работе [2]. Поэтому направляющие косинусы a', Р', у' оси п' и попарные разности А , А^ окончательно запишутся в следующем виде:

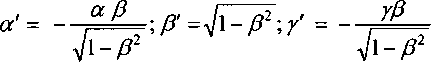
Jnn, (2p2-}KaJxy+yJyz) + Py(2aJzx-ypx) v = —/    '■■---------—9-----------------;(3)

' р^р2Р^-РЪ

Jnn. (2р2-l)(aJ +yJ ) +Pa(2yJzx+ahzx)

^ =..  ---------------------------------.(4)

р^р2

Разность Azx должна вычисляться по формуле:

Ам —'lUm’m - Jzx COS ШЭД , где J_x, Jm-m, Jn „, - центробежные моменты изделия (показания балансировочного станка); р -угол наклона изделия на станке; а, Р,у - направляющие косинусы оси вращения.

В практических расчетах разности Axv, Avz удобнее вычислять не по формулам (3), (4), а с помощью вспомогательной величины Дя:

2pxpJxy + pyJyz + ya J^—

.       ^ии'

pjl-p2x

AX=A„--;k=-k„^a".

По определенным попарным разностям A_XJ, \_yz, \_zx и центробежными МИ J_yz, J_zx, J_xv можно вычислить ориентацию всех трех главных осей инерции твердого тела и найти оценки его осевых МИ [1, 2].

В данной работе мы рассмотрим возможность уточнения приближенных значений осевых МИ J'x,J'y,J'z, полученных расчетом по чертежам изделия, в том числе при его компьютерном проектировании.

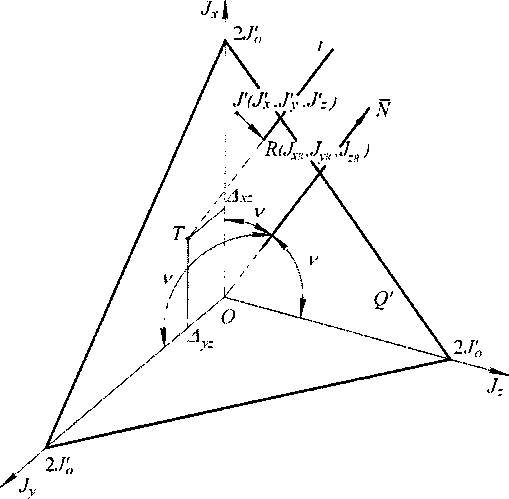
Изобразим систему координат OJ_xJ_yJ, и точку J' с координатами: J'_X,J'_V,J'_Z (см. рисунок). Соотношения осевых МИ выбрано наиболее типичным для таких изделий машиностроения, как автомобильные колёса, вентиляторные диски, отрезные и шлифовальные круги: J_X>J_V>J_:>0, J_y~J_. Отсюда следуют соотношения для попарных разностей: Д_х>,>0, Д_у, >0, Д,_х<0, д,₂ «0,|д>|д_2Х|,^^

Уравнения (1) описывают плоскости, параллельные осям J₂,J_X,J_V соответственно. Система линейных уравнений (1) имеет ранг, равный 2. Поэтому три плоскости пересекаются по одной прямой t. Эта прямая имеет равный угол наклона

Расчет и конструирование v = arccos—L = 54°44'8,2'' к каждой из осей

V3                                   * у

Прямая t пересекает координатную плоскость J_xOJ_y в точке Т (А_х,,А_у,,0) и параллельна вектору N, совпадающему с биссектрисой трехгранного угла, образуемого координатными плоскостями. Ясно, что все точки ^J_x, J _v, J,\ удовлетворяющие системе уравнений (1), должны лежать на этой прямой. Из них только одна точка соответствует сочетанию действительных осевых МИ изделия. Мы должны выбрать на этой прямой точку, которая является наилучшей оценкой действительных МИ. Приближенные значения J'_x,J'_y, J'. нам известны. Примем, что наилучшей оценкой является точка R, расположенная к точке J' ближе всех остальных точек данной прямой t, т. е.на перпендикуляре, опущенном из точки J* на прямую t. Методами аналитической геометрии находим координаты точки 7?:

«7Т+ JА х — А J + J* + J’ + А — A J' + J' + J'. + А — А т _ X у Ь xy ^Х -г _ X у и yz xy , т _ х V             ZX VZ /о\

^Jx            _        , J _у         ¹ ™          S ^J zR™"          ~          • W

Рассмотрим смысл полученного результата. Возвратимся к системе (1). Если эту систему дополнить уравнением

Л+У,+Л=2Л                                         (9)

и полагать, что величина полярного момента инерции изделия J_o нам известна, то уравнение (9) определяет плоскость (с направляющим вектором N ), отсекающую на координатных осях одинаковые отрезки, равные 2 J_o . Эта плоскость перпендикулярна прямой t. В каждой точке этой плоскости удвоенная величина полярного момента инерции рассматриваемого твердого тела (относительно полюса О) равна 2 J_o.

Решая уравнения (1), (9), т. е. определяя координаты точки пересечения прямой t и плоскости (9), получаем

J_x-^J₀*\_xy -A J; J_y J^2J₀^_y2-b_xy\ J₂ =~(2J_o+^_x-\_yz).

Поскольку точное значение 2 J_o в реальной ситуации нам не известно, то в качестве его оценки мы принимаем расчетное значение суммы

2j;=j;+j;+z,

т. е. плоскость Q с направляющим вектором N проводим через точку J{J_x,J_y,J₂) и находим координаты точки 7? пересечения плоскости Q и прямой t. Значения этих координат и определяются соотношениями (8).

Несколько меньшие уточненные значения осевых моментов инерции мы получим, проведя через точку J не плоскость Q, а сферу с центром в начале координат и с радиусом равным не арифметической сумме расчетных моментов, а их «геометрической» сумме.

Приближенные значения осевых МИ на практике обычно получают после расчета характеристик геометрии масс изделия по его чертежу. Использование в расчетах фактических значений размеров готовых деталей несколько повышает точность расчета; но все равно в большинстве случаев она остается довольно низкой из-за неравноплотности материала по объему и отклонения формы деталей от теоретического контура. Не удаётся обычно в расчетах учесть также смещения и перекосы деталей в пределах зазоров, резьбы, накатанные и рифленые поверхности и другие сложные элементы. По некоторым сведениям ошибки теоретического расчета МИ по чертежу для сложных узлов составляет 5-10%.

Иванов И.И., Тверской М.М.                             Уточнение расчетных значений осевых_______________________________________________________моментов инерции твердого тела...

Следует отметить и то обстоятельство, что степень соответствия найденных уточненных значений J_xR, J_yR, J_zR действительным значениям зависит от точности расчета не отдельных значений, J_x, J_y, J_z, а их суммы, что следует из выражений (8). Проиллюстрируем сказанное примером.

Допустим, что некоторое тело имеет следующие действительные значения МИ: J_x =16, J_y = 12, J. = 11. Тогда J_x + J_у + J_ = 39, Д = 4, Д „. = 1 , Д _zx = -5 . Расчетные значения: /_Л=15, ^—12,5, Л =11,5, J_x + J_y + J, =39 . Уточненные значения: J_xR =^(39 + 4 + 5) = 16, ^=|(39 ₊ 1-4)=12, _Лд=1(з9-5-1) = 11.

Несмотря на достаточно грубый расчет моментов J_х, J_v, J,, «удачное» сочетание допущенных ошибок привело к их полной взаимной компенсации (2J_O = 2J₀ = 39). Это позволило получить уточненные значения моментов, J_xR, J_yR, J ,_R, равные их действительным значениям.

Степень уточнения зависит и от точности определения разностей моментов Д ,Д jA^ с помощью балансировочного станка [1,2]. Современные станки для динамической балансировки имеют высокую точность. Поэтому для сложных изделий в подавляющем большинстве случаев будет иметь место существенное уточнение исходных расчетных МИ J_x,J'_y,J_z.