Уточненное описание управляемого движения верхней конечности при активации скелетной мышцы

Эффективность управляемого движения тела человека во многом определяется текущим состоянием скелетных мышц. В настоящее время накоплен большой объем экспериментальных данных о биомеханических свойствах мышц и предложены модели для их структурно-функционального анализа. Реализация сократительной функции на микроуровне рассматривается как относительное скольжение актиновых и миозиновых нитей саркомера, обусловленное действием поперечных мостиков [16, 19, 24]. Упрощенный вариант описания данного процесса [3, 14], основанный на гипотезе

Шилько Сергей Викторович, к.т.н., заведующий лабораторией, Гомель Черноус Дмитрий Анатольевич, к.т.н., в.н.с., Гомель скользящих нитей, позволяет прогнозировать изменение зависимости текущей длины активированной мышцы, скорости сокращения и генерируемой силы во времени. В результате экспериментальных исследований препаратов мышечных тканей и частично извлеченных мышц [20], а также миометрических измерений в режиме in vivo [1, 17, 18] были определены диапазоны значений механических характеристик мышц в пассивном состоянии. Установлено, что скелетная мышца в пассивном состоянии при продольном удлинении деформируется как нелинейно-вязкоупругий объект, реономные свойства которого можно описать простым экспоненциальным ядром с одним временем релаксации [2]. Ранее авторами была предложена обобщенная модель скелетной мышцы [15], позволяющая по данным миометрии определить комплекс деформационных параметров мышцы, важных для описания процесса активации сократительной функции.

Учет биомеханических свойств скелетных мышц в формировании управляемых движений элементов опорно-двигательной системы возможен в рамках «веревочных» шарнирно-стержневых моделей [4, 8], в которых предполагается, что кости скелета являются жесткими массивными стержнями, соединенными в шарнирах (суставах). Скелетные мышцы моделируются нелинейно-вязкоупругими нитями (тягами). Вариант использования подобной модели был представлен в работе [15].

Вместе с тем для корректного описания работы активной тяги обобщенная модель скелетной мышцы нуждается в модификации, поскольку активная тяга является комбинированным объектом, образованным мышцей и системой соединительных тканей, в том числе сухожилиями. При моделировании процесса активации сухожилие можно считать нелинейно-вязкоупругим элементом, последовательно соединенным с мышцей. В ранее предложенной модели скелетной мышцы [17] этот элемент не учитывался. Отмеченная ограниченность модели существенно снижала точность расчетных оценок и не позволила сопоставить результаты моделирования с известными из литературных источников [6, 13] данными фотометрических исследований управляемых движений. В некоторых известных моделях скелетных мышц [9, 14] присутствуют упругие и вязкие элементы, которые могут быть поставлены в соответствие сухожилию, но при этом принимается допущение о линейной связи напряжений и деформаций упругого элемента.

Целью настоящей работы является описание движения элемента опорнодвигательной системы в процессе активации скелетной мышцы при комплексном учете вязкости и нелинейности деформирования соединительных тканей.

Модель эквивалентной тяги

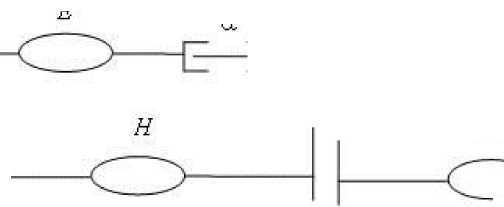
Ранее предложенная модель скелетной мышцы [15] образована тремя элементами (рис. 1, а). Нелинейно-вязкоупругий элемент Н описывает деформирование оболочки мышцы. Нелинейно-упругий элемент Е описывает деформирование актиновых и миозиновых нитей при сокращении мышцы. Сократительный элемент α вводится для формализации актомиозинового взаимодействия. При моделировании эквивалентной тяги, образованной мышцей и соединительными тканями, к трем перечисленным элементам последовательно присоединяется нелинейно вязкоупругий элемент S (рис. 1, б), описывающий деформирование сухожилия. Элемент Н характеризует деформирование мышцы в пассивном состоянии (при выключенном элементе α). Так как пассивная мышца не оказывает существенного влияния на механические свойства сухожилия [20], можно принять, что характеристики элементов S и Н совпадают. Ввиду того что жесткость соединительных тканей на порядок меньше жесткости нитей саркомера [3, 19], при последовательном соединении элементов Н и Е можно пренебречь деформацией последнего.

а

Рис. 1. Обобщенная вязкоупругая модель мышцы ( а ) и модель эквивалентной тяги ( б ): E – нелинейно-вязкоупругий элемент, характеризующий деформативность актиновых и миозиновых нитей саркомера; H – нелинейно-вязкоупругий элемент, характеризующий деформацию мышцы в пассивном состоянии; S – нелинейновязкоупругий элемент, характеризующий деформирование сухожилия;

a - сократительный элемент, характеризующий актомиозиновое взаимодействие

б

На рис. 2 показана модель эквивалентной тяги, где вышеуказанные допущения не являются принципиальными и введены для упрощения математической модели. Характеристики элемента H выбираются так, чтобы система из двух указанных элементов, соединенных последовательно, соответствовала деформированию сухожилия совместно с пассивной мышцей.

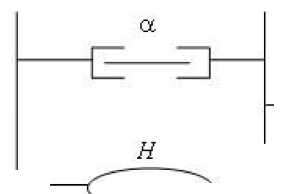
Рис. 2. Упрощенная модель эквивалентной тяги. Обозначения те же, что и на рис. 1

Работа сократительного элемента при максимальном уровне активации описывается системой дифференциальных уравнений [14, 17]

• ⁵    = k i [ z( £ ^- £ посл ) ^- 5 ^- n ^- m ^- p ] ^- k 4 5 , n = k 4 ^{5 -} d 8 n |^{£ - £} посл | , m = — k 2 m + d 8 n |^£ — ^£ посл | ,

  p = ^- к з p

  
  

при ^£ ^ ^£ посл и

• ⁵    = ^k 1 [ z^{( £-£} посл ) — ⁵ — n — m — P ] ^{- k} 4 ⁵ ,

n = ^k 4 ⁵ — d 8 n |^£-£ посл| , m =— ^k 2 m , p = — ^k 3 P + ^d 3 n |^£-£ посл |

(1а)

(1б)

при £ > £

Здесь s, n, m, p – число пассивных, тянущих, тормозящих и супертянущих поперечных мостиков соответственно, отнесенное к общему числу мостиков на половине длины саркомера a; k, k2, k3, k4 - временные константы образования и разрыва мостиков; ds = 137,5 - константа, равная отношению половины длины недеформированного саркомера к расстоянию между положениями равновесия тянущего и тормозящего мостика; г, £посл - продольная деформация эквивалентной тяги и последовательно соединенного с сократительным вязкоупругим элементом соответственно; z(еа) - кусочно-линейная функция деформации сократительного элемента (разность между £ и £п0сл), описывающая зависимость числа мостиков а от текущей длины саркомера.

0,   £  < - 0,375;

а

1,545 + 4,12г_а,   - 0,375 <£<- 0,167;

z ^{( £} а ) =

1 + 0,856 г а ,   - 0,167 <£ а < 0;

• 1,  0 <£ а < 0,125;

1,177 - 1,412 s ,  0,125 < г < 0,833;

а              а

^ 0,   £_а> 0,833.

Точка над символом в (1) и далее означает производную соответствующей величины по времени.

Система уравнений (1) описывает режим активации мышцы, соответствующий гладкому тетанусу [20]. Для анализа других режимов активации скелетной мышцы в первое уравнение системы вводится функция частоты и амплитуды стимулирующих импульсов [12]. В рамках настоящей работы будем рассматривать только тетаническое сокращение, описываемое уравнениями (1) без необходимости введения вышеуказанной функции.

Связь осевого напряжения о_я c продольной деформацией £^ для нелинейновязкоупругого элемента Н может быть выражена дифференциальным уравнением [17]

СТ H + - ^ H = Q а^ С2 £ H exp (С*2 £ H )+ ^(exp (С2 £ н )- 1)

т        1-yL                 т

Здесь о. - удельная мышечная сила (отношение максимальной силы, генерируемой мышцей в изометрических условиях, к площади физиологического поперечника); C , C – константы, которые с приемлемой точностью могут быть приняты равными 0,05 и 2,4 соответственно для всех скелетных мышц [5]; Y - параметр ядра релаксации мышечной ткани ( у = 0,681 [17]); т - время релаксации мышечной ткани.

Для элемента, параллельно соединенного с сократительным, соотношение (3) примет вид

1 C

G + "% = ^ а ~

С2 (£ - £посл ) еХР (С2 (£ - £посл )) + ^(exP (С2 (£ - £посл )) - 1)

где апар - осевое напряжение в параллельно соединенном вязкоупругом элементе.

Для последовательно соединенного элемента получим о+-о=оа т

С _.                х 1-V/

1          2 посл р\  2 посл /          \ р\  2 посл /    /  ,

• 1    - Y L                          т                     _

где σ – эффективное осевое напряжение в эквивалентной тяге, определяемое соотношением

о =

T a

S 0

= (i - kS )Опар + kS° a ( n — m + 2 Р ) .

Здесь k – коэффициент, равный отношению физиологического поперечника S мышцы к эффективной площади поперечного сечения S эквивалентной тяги; T – усилие натяжения в эквивалентной тяге.

Уравнения (1), (4)–(6) позволяют установить связь осевого напряжения и продольной деформации эквивалентной тяги при активации мышцы. Для пассивной тяги зависимость о(а) совпадает с он (ая) и определяется уравнением (3).

Описание движения элемента опорно-двигательной системы

Рассмотрим движение упрощенной двухстержневой модели верхней конечности человека (рис. 3) при активации эквивалентного сгибателя. Стержень 1 модели, имеющий длину l и массу m , моделирует плечевую кость. Стержень 2 длиной l и массой m моделирует кости предплечья. Шарнир A относится к плечевому, а шарнир B – локтевому суставу. На конце стержня 2 закреплена точечная масса m , соответствующая поднимаемому рукой грузу. Эквивалентная тяга 4 , моделирующая двухсуставную мышцу (бицепс), крепится на расстоянии b от шарнира B и к неподвижному шарниру A . Малый стержень длины b перпендикулярен стержню 2 и жестко связан с ним. Этот стержень не имеет собственной массы и моделирует «плечо» бицепса в локтевом суставе [13].

При активации тяги груз 3 будет подниматься. В качестве обобщенных координат системы выберем углы ^ и ф₂ отклонения стержней 1 и 2 от вертикального положения против хода часовой стрелки. В этих координатах уравнения Лагранжа второго рода [11] для рассматриваемой модели примут вид

..                                                       ..                                                     .

ф] l2 I - m + m ₂ + m ₃ I + ф₂ 2 lj_c cos ( ф 2 — ф1 ) — ф 2 2 Ус sin ( ф 2 — Ф1 ) =

— /m + m ₂ + m₃

g sin ф 1 ^{— l} T_a cos ( ф 2 ^— ф 1 ^— P _a ) ,

m + 3 m + 4 mm              .

ф 2 ¹ 2   2     3 -----⁺ Ф 1 ² l i l C cos № ^— Ф 1 ) ⁺ Ф 1 ² l i l C sin ( ф 2 -ф 1 ) =

3 (m2 + m3)

= ^- l C ( ^m 2 + m 3 ) g sin ф 2 + bT_a sin ( P a ) •

Здесь для краткости записи введены обозначения

1 ₂ ( m ₂ + 2 m ₃)

1c =      ------ \ , P_a = ar^csin

Ca

l i cos ⁽ф 2 ^-ф 1 )

_v V l i² + b ² - ² l i b sin ⁽ф 2 ^-ф 1 ) _v

.

Текущая длина активной тяги может быть выражена через углы ф, и ф2. Для относительного удлинения (продольной деформации) тяги получим

а =

l_x + b — 2 1дЬ sin ( ф₂ — ф| )

l + Ь

— i.

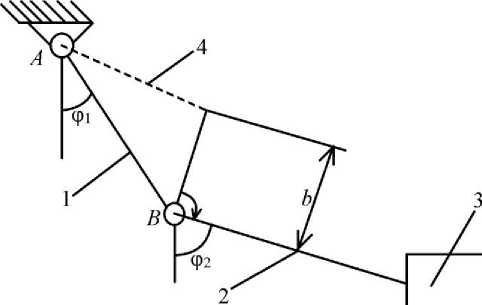
Рис. 3. Двухстержневая модель верхней конечности: стержень 1 моделирует плечевую кость; стержень 2 – кости предплечья; 3 – груз; тяга 4 – бицепс; шарнир A – плечевой сустав; шарнир B – локтевой сустав

Используя совместно соотношения (1), (4), (5), (7) с учетом (6), (8) и (9), получим систему восьми дифференциальных уравнений для определения временных зависимостей числа пассивных s , тянущих n , тормозящих m и супертянущих p поперечных мостиков, деформации £_посл и напряжения ст_па, углов отклонения ф₁ и ф₂. Явный вид данной системы не приводится в силу ее громоздкости. Численное решение системы дифференциальных уравнений при начальных условиях 5 (0) = 1 , n (0) = m (0) = p (0) = £_mra (0) =П пар (0) =ф 2 (0) = ф 1 (0) =^ 1 (0) = 0, <о ₂(0) = 0 реализовано в программном продукте MathCad .

В качестве примера использования разработанной математической модели рассмотрим подъем рукой груза массой т₃ = 30 кг, результаты анализа кинограммы которого приведены в работе [7]. Исходные данные для двухстержневой модели следующие [24]: т_х = 1,1 кг; m₂ = 0,83 кг; 1_г = 0,3 м; /₂ = 0,34 м; b = 0,02 м. Значения временных констант, определяющих актомиозиновое взаимодействие при активации мышцы, заимствованы из работы [17]: к = 85,513 c^-1; k₂ = 316,25 c^-1; k₃ = 32 е^-1; к₄ = 122,192 е^-1. В соответствии с работой [6], удельная мышечная сила бицепса принята равной с_а = 11,4 кг/см² = 1,12 МПа, а по результатам исследования [12] время релаксации для данной мышцы составляет т = 35 мс. Физиологический поперечник мышцы Sy = 20 см² и коэффициент k_s = 0,8 подобраны таким образом, чтобы результаты расчета относительного угла поворота стержней модели Дф = ф₂ — ф₃ совпали с данными кинометрии [7] при t = 1,5 е; значение 8^ оказалось близким к среднестатистическому значению (23 см²) для данной мышцы [6].

На рис. 4 представлено сопоставление расчетных временных зависимостей величины Дф с экспериментальной. Можно отметить, что учет последовательного и параллельного нелинейно-вязкоупругого элемента позволяет получить более точные расчетные оценки кинематических параметров управляемого движения. Кроме того, в рамках усовершенствованной методики удается описать такие явления, как задержка начала движения при активации мышцы и наличие затухающих колебаний звеньев опорно-двигательной системы около равновесного состояния. Под задержкой здесь подразумевается начальный промежуток времени, в течение которого движение системы практически отсутствует. В рассматриваемом примере величина задержки составила порядка 0,08 с. На расчетной временной зависимости (см. рис. 4) данному участку соответствует пренебрежимо малое возрастание угла Δϕ . Наличие задержки, которая не обнаруживается при отсутствии элемента S в модели эквивалентной тяги (см. рис. 1), обусловлено, по-видимому, вязкостью соединительных тканей. При этом в эквивалентной тяге реализуется амортизация резкого возрастания генерируемой мышцей силы.

На втором этапе движения (от 0,08 до 0,4 с) отмечается значительная скорость роста исследуемой кинематической характеристики. При t > 0,4 c система совершает затухающие колебания около положения равновесия. В рассматриваемом примере период угловых колебаний Δϕ составляет 0,55 с. При t > 1,5 c эти колебания практически прекращаются. Подобные колебания являются характерным режимом движения для рассматриваемой динамической системы, содержащей массивные тела и упругие связи. В рамках модели, описанной в работе [23], деформируемость сухожилия не учитывается, что ведет к существенно завышенной расчетной оценке жесткости эквивалентной тяги. Прогнозируемые значения амплитуд колебаний системы около равновесного состояния оказываются более чем на порядок меньше соответствующих значений, полученных с учетом деформирования соединительных тканей (см. рис. 2). На кривой 2 (рис. 4) колебательное движение не выявляется.

На рис. 5 представлены расчетные временные зависимости силы натяжения T a в эквивалентной тяге. Можно отметить, что на начальном этапе активации (порядка 0,05 с) происходит скачкообразное увеличение силы T a . В дальнейшем рост силы в тяге происходит линейно вплоть до достижения максимального значения. Изменение силы T a при t > 0,3 c можно охарактеризовать как затухающие колебания около значения, соответствующего статическому равновесию системы. Продолжительность начального участка диаграммы T a ( t ), скорость роста на втором участке и амплитуда колебаний силы при t > 0,3 c возрастают при увеличении времени релаксации τ материала сухожилия.

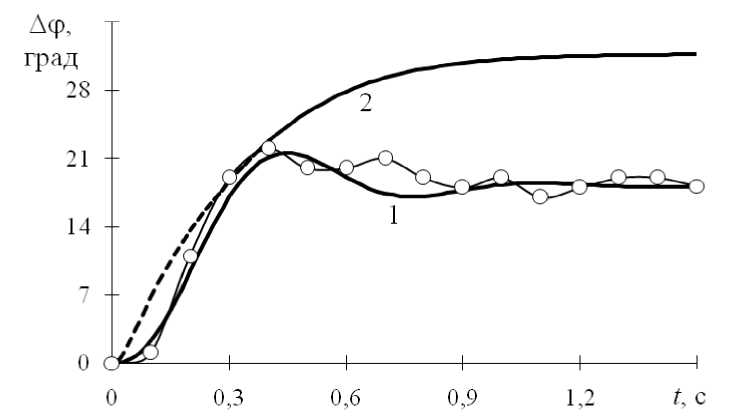
Рис. 4. Временная зависимость относительного угла поворота в локтевом суставе при подъеме груза: кривая 1 – расчет по разработанной методике; кривая 2 – расчет по методике работы [23], точками показаны результаты кинометрии из работы [6]

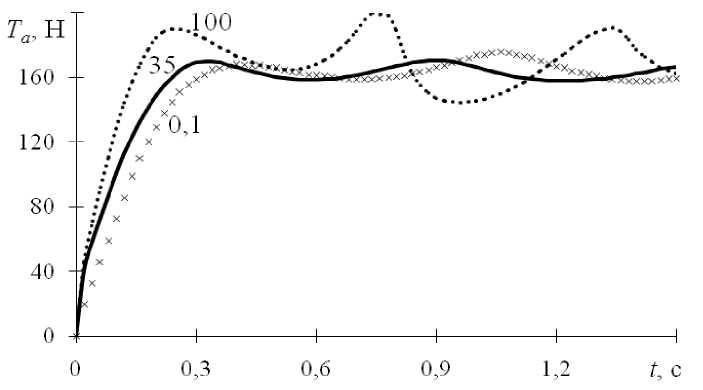
Рис. 5. Временные зависимости силы натяжения в эквивалентной тяге. Числа у кривых соответствуют значению времени релаксации τ , мс

Помимо очевидных биомеханических приложений (рационализация спортивных тренировок и трудовой активности [10]), разработанная модель представляет также интерес для воспроизведения мышечной активации в «умных» материалах высокомолекулярной природы, используемых, в частности, при создании интеллектуальных приводов машин и механизмов, а также конструкций управляемой конфигурации [21, 22].

Заключение

Показана возможность уточненного описания управляемого движения основных элементов опорно-двигательной системы с использованием модифицированных шарнирно-стержневых моделей, в которых мягкие биоткани (мышцы и сухожилия) представлены в виде нелинейно-деформируемых объектов. На примере подъема груза верхней конечностью показано, что предложенная формализация процесса актомиозинового взаимодействия и нелинейно-вязкоупругого деформирования сухожилий обеспечивает приемлемую точность расчета кинематических и силовых параметров. Модель может быть использована для рационализации спортивных тренировок и трудовой активности, а также при проектировании интеллектуальных приводов и конструкций управляемой конфигурации.

Б ЛАГОДАРНОСТИ

Исследование выполнено при финансовой поддержке государственной программы научных исследований «Конвергенция» (задание К3.06.13) и совместного белорусско-корейского проекта Т18КОРГ-004.