Вариационно-разностный метод решения трехмерных задач электропроводности в гиротропных средах

Исследование выполнено за счет гранта Российского научного фонда № 2227-00006,

Задача рассматриваемого вида возникает, например, при математическом моделировании квазистационарных электрических полей и токов в глобальном проводнике, состоящем из ионосферы и атмосферы Земли, при использовании декомпозиции области. При этом выделяется D-слой ионосферы Земли, лежащий на высотах 50 - 90 км над эллипсоидом, соответствующим среднему уровню моря. Верхняя и нижняя границы могут быть смещены на несколько километров для оптимизации декомпозиции. В D-слое неприменима двумерная модель, адекватная для более высоких слоев, и проводимость перестает быть скаляром, как в лежащей ниже атмосфере. Поэтому в этом слое необходимо решать трехмерную задачу электропроводности с гиротропным тензором проводимости. В рамках метода декомпозиции возникают смешанные граничные условия на границах D-слоя: условие идеальной проводимости на верхней границе и условие на идеальном изоляторе – на нижней. Оба условия – неоднородные. Отметим, что к аналогичным краевым задачам можно свести математические модели теплопроводности или диффузии в движущихся средах [2 , 12] .

Для такой задачи в [11] предложена новая формулировка краевой задачи с симметричным положительно определенным оператором. Новыми неизвестными функциями является пара специальных потенциалов, скалярного и векторного. Построен квадратичный функционал энергии, к минимизации которого сведено решение краевой задачи.

В настоящей работе строится метод численного решения этой краевой задачи.

• 1    Задача электропроводности

В занятой проводником трехмерной области напряженность электрического поля E = (E x , E y ,E z ) и плотность тока J в квазистационарном приближении удовлетворяют закону Фарадея, закону сохранения заряда и закону Ома:

div J = Q, rot E = G , J = E. (1)

где G = 0, если есть заданное магнитное поле, изменяющееся со временем, Q = 0, если есть сторонние токи, <г — проводимость. Проводимость некоторых веществ в магнитном поле, например, плазмы в ионосфере Земли, является гиротропным тензором. В декартовых координатах x, y, z с осью z , направленной вдоль вектора магнитной индукции B , тензор проводимости имеет вид:

(aP  -aH  0\ aH   aP    0    .(2)

о     о    ^k)

Его компоненты называются продольной (^k), Педерсеновской (aP) и Холловской (ан) проводимостями [13]. Будем также использовать Кау-линговскую проводимость ас = (aP + aH )/ар.

В статье [4] рассмотрены а более общего вида. Здесь, как и в [11] , мы используем вид (2) , чтобы получить более точные оценки, важные для численного решения задач. Поскольку прохождение электрического тока сопровождается диссипацией электрической энергии с плотностью J • E , симметричная часть а положительно определена. Для тензора вида (2) это означает положительность диагональных элементов. Исключив из рассмотрения идеальные проводники и изоляторы, мы предполагаем равномерную в области Q ограниченность всех коэффициентов а и равномерную положительную определенность. Удобно записать эти условия в виде:

σ 1 ≤ σ _C ≤ σ 2 ,     σ 1 ≤ σ _k ≤ σ 2 ,                    (3)

где σ 1 , σ 2 — положительные константы.

Мы называем параметром неоднородности отношение, которое характеризует неоднородность проводника:

H = ^а 2 ^/а 1 .                                ⁽⁴⁾

Предполагаем, что область Q — ограниченная и гомеоморфна шаровому слою. Ее внешняя Г и внутренняя y границы — гомеоморфные сфере дважды непрерывно дифференцируемые поверхности. Нормальную (положительное направление наружу) и касательные к границе компоненты векторов будем отмечать индексами n и τ , ∗ означает транспонирование.

Чтобы провести все доказательства простыми средствами, в статье [11] наложены дополнительные ограничения на форму области, которые по сути означают близость границ к двум концентрическим сферам. Форма D-слоя ионосферы этим ограничениям удовлетворяет.

Когда рассматриваемая область граничит с идеальным изолятором, на границе обращается в нуль нормальная компонента J . На границе с идеальным проводником обращаются в нуль касательные компоненты E . В методе декомпозиции эти условия неоднородны:

J n \ Y = q,      E T | г = g ,                           ⁽⁵⁾

где q, g — заданные функции.

Для разрешимости задачи (1, 5) правые части должны удовлетворять некоторым ограничениям. Во-первых, необходимо div G = 0,                              (6)

так как div от rot тождественно равна нулю, и без (6) не может быть выполнено первое уравнение (1) . Вычислим нормальные к границе компоненты rot от левой и правой частей второго граничного условия (5) :

rot n E t | r = rot n g | r .

Полученная левая часть также удовлетворяет первому уравнению (1) . Это налагает на заданные функции второе необходимое для разрешимости задачи условие

G n | r = rot n g | r .                               (7)

В следующем параграфе приведена формулировка новой задача с оператором, сопряженно факторизованным по определению [6] , решение которой является решением исходной задачи (1 , 5) . Из существования решения новой задачи следует существование решения исходной, а единственность в [11] доказана независимо.

• 2    Энергетический метод

Мы используем энергетический метод [7] . Приведем основные формулировки из работы [11] , в которой проведены все необходимые доказательства.

Будем рассматривать множество пар гладких функций F , P , удовлетворяющих условиям:

F | r = 0, P n | r = 0, P t I y = 0.                     (8)

Будем обозначать квадратными скобками симметричную билинейную форму:

1 ∗

σSσ - σS    grad F

σ ₀

• -Sa *    0 S s / V rot p /

+div v div P ) dQ, (9)

где u, v и F, P — пары гладких функций, удовлетворяющих условиям (8) , E) — симметричная положительно определенная матрица, которую мы выберем позднее, как и значение положительной константы σ ₀ .

Эта билинейная форма играет роль энергетического скалярного произведения, она симметрична и положительно определена.

Чтобы получить более точные оценки, использован специальный вид a (2) и ограничения (3) . Также выбраны

О о = V ^ 1 ^ 2 ,  S ¹ = (о + а )/2.

Получены неравенства, означающее положительную определенность билинейной формы (9)

[ ( P ) , ( P ) 1 >  сШ /(F 2 + | P | 2 ) d^,          (11)

а также оценки значений (9) снизу и сверху через сумму квадратов норм F и декартовых компонент P как элементов пространства W 2(1) (Q). Такие оценки означают эквивалентность введенной энергетической нормы норме пространства W 2(1) (Q). В частности, это позволяет при численном решении задачи использовать те же аппроксимирующие функции, что и для уравнения Пуассона.

В соответствии с энергетическим методом [7] определим функционал энергии:

W (F, P ) = ₂[( _P ),( _P )1 —

• - У FQdQ - У P * G dQ + У У FqdY + j P * g dr.     (12)

Линейные функционалы являются ограниченными в предположении, что функции Q, G x , G y , G z ограничены в норме L 2 (Q), q — в норме L 2 ( y ), g x ,g y ,g z — в норме L 2 (r). Поскольку квадратичная часть положительно определена и линейная — ограничена, в энергетическом пространстве существует, причем единственный, элемент F , P , доставляющий функционалу энергии минимальное значение.

Введем обозначения

E = - —Sa * grad F + S?rot P , J = 4 E .            (13)

σ 0

Элемент, доставляющий функционалу энергии минимальное значение, при дополнительном предположении гладкости, является решением следующей краевой задачи div ( ^oScFgrad F +--aS rot P ) = Q/ao,

σ02

rot (Sa*grad F + Srot P) = G,(14)

1                              I

--SS Sier grad F +-- er Si rot P ) σ ₀2                  σ _{0            n}

Sier * grad F + S rot P )

σ 0                        τ

= q^/s 0 ,

γ

= g .

Γ

Эти уравнения с учетом обозначений (13) совпадают с уравнениями и граничными условиями исходной краевой задачи (1, 5), с дополнительным уравнением div P = 0. (17)

Оно позволяет выделить единственную функцию P из множества эквивалентных с точки зрения формулы (13) , в которую входит лишь rot P . Действительно, J , E (13) не изменяются при добавлении к P градиента произвольной функции.

Граничные условия (8) являются главными, то есть им должны удовлетворять функции, на которых ищется минимум, а граничные условия (15 , 16) — естественные, то есть выполняются как следствие минимизации.

Доказано и обратное утверждение: решение задачи (14, 15, 16, 17, 8) доставляет функционалу энергии минимальное в энергетическом про- странстве значение.

Если предположение о гладкости не выполнено, пару функций F, P , доставляющую функционалу энергии минимальное значение, считаем обобщенным решением задачи (14 , 15 , 16 , 17 , 8) , а построенные по ним E и J — обобщенным решением исходной задачи (1 , 5) .

Поскольку доказаны существование и единственность обобщенного решения задачи (14 , 15 , 16 , 17, 8) , тем самым доказано существование обобщенного решения исходной краевой задачи (1, 5) , и для нее обоснован принцип минимума функционала энергии.

Поскольку в результате минимизации функционала энергии выполняется равенство (17), минимизацию можно проводить в подпространстве, выделенном условием

У (div P ) ² dQ = 0.

Тогда с учетом обозначений (13) при выбранном в соответствии с (10) тензоре S можно квадратичную форму, соответствующую энергетическо- му скалярному произведению (9), записать в терминах исходной задачи электропроводности (1, 5):

σ 0

У E * J dQ.

Произведение E∗J есть плотность джоулевой диссипации, то есть со- провождающее прохождение электрического тока выделение тепловой энергии. Равенство значения квадратичной формы (9) полной джоулевой диссипации в области Q оправдывает ее название «энергетическая».

• 3    Линейные функции в тетраэдре

Используя принцип минимума квадратичного функционала энергии, применим вариационно-разностный метод [8] , который можно рассматривать как одну из эффективных реализаций метода конечных элементов. Достаточно разделить область Q на тетраэдры и использовать кусочнолинейные аппроксимирующие функции для каждой из четырех неизвестных функций, которыми являются F и декартовы компоненты P . Тогда уравнения вариационно-разностной схемы получаются как условия минимальности функционала энергии, то есть равенство нулю его производных по значениям кусочно-линейных функций F, P _x , P y , P _z в узлах сетки.

Поскольку энергетическая норма эквивалентна сумме норм F и декартовых составляющих P как элементов W^ ¹)^ ), справедливы известные свойства кусочно-линейной аппроксимации [1] , в принципе позволяющие строить сколь угодно точные приближения к точному решению задачи.

Мы используем блочно-структурированные сетки, состоящие из криволинейных шестигранников. Мы строим сетку на нижней границе D-слоя ионосферы, проецируя равномерные прямоугольные сетки, построенные на гранях параллелепипеда, вершины которого лежат на уровне моря, то есть на эллипсоиде вращения. В объеме D-слоя мы получаем узлы сетки, деля на равные интервалы вертикальные отрезки, идущие от нижней до верхней границы.

Чтобы использовать кусочно-линейные функции, каждую ячейку «кубической» сетки следует разделить на тетраэдры. Мы делаем это, определяя некоторый центр ячейки и центры ее шести граней. Термин «куб» мы употребляем в смысле нумерации узлов сетки, в реальности это пространственная фигура с 8 вершинами. Затем каждая грань естественным образом делится на четыре треугольника, а ячейка делится на 24 тетраэдра так, что центр ячейки является одной из вершин каждого тетраэдра. Разумеется, должны быть соблюдены условия невырожденности получающихся тетраэдров [1] . Значения кусочно-линейной функции в этих центрах получаются путем некоторой интерполяции узловых значений, обычно, как их среднее арифметическое.

Прежде, чем строить уравнения вариационно-разностной схемы, запишем в векторной форме закон Ома, из которого получен тензор а вида (2) :

j k = а „ E k , j _± = a p E _± - а н [ E _± x B ] /B. (19)

Здесь индексами ||,^ отмечены компоненты вектора вдоль и поперек вектора магнитной индукции B . Обозначим через b = (b x ,b y ,b z ) единичный вектор B / | B | . Тогда тензор проводимости из (19) может быть записан в декартовых координатах в виде

^ = (^ k ^{- a} p )

b _x b _x b y b _x b z b x

b x b y b x b z \              /  0

by by  by bz I +aP I+aH    bz bzby  bzbz                    -by

- b z    b y \

0    - b x    , (20)

b x    0

который более удобен для вычислений. Здесь I — единичная матрица. Выражение (20) может быть также получено из (2) поворотом системы координат.

Рассмотрим отдельный тетраэдр с постоянной проводимостью и линейными функциями F, Px , Py , Pz . Две вершины каждого построенного тетраэдра совпадают с узлами кубической сетки. Присвоим им номера 1, 2 в таком порядке, что грань обходится по часовой стрелке, если смотреть из центра ячейки. Вершиной номер 3 считаем центр кубической ячейки. Вершиной номер 4 будет центр грани кубической ячейки. Обозначим че- рез r1 , r2, r3 векторы, соответствующие отрезкам, соединяющим вершину 4 с остальными тремя. Через e1 , e2 , e3 обозначим опущенные из этих вершин высоты, разделенные на квадраты их длин h1 , h2, h3. Несложно получить выражения для градиента, ротора и дивергенции через значения линейных функций F, Px , Py , Pz в четырех вершинах тетраэдра:

grad F = (F i - F 4 ) e i + (F 2 - F 4 ) e 2 + (F 3 - F 4 ) e 3

rot P = (P i,x - P 4,x ) a i + (P i ,y - P 4 ,y ) b i + (P i ,z - P 4 ,z ) c i

^{+ (P} 2 ,x ^- P 4,x ^{) a} 2 ^{+ (P} 2 ,y ^- P 4,y ^{) b} 2 ^{+ (P} 2 ,z ^{- P} 4,z ^{) c} 2

^{+ (P} 3 ,x ^{- P} 4,x ^{) a} 3 ^{+ ( P} 3,y ^{- P} 4,y ^{) b} 3 ^{+ ( P} 3,z ^{- P} 4,z ^{) c} 3

div P = ( P i - P 4 ) * e i + ( P 2 - P 4 ) * e 2 + ( P 3 - Р 4 ) * е з ,       (21)

где в соответствии с

правилом вычисления ротора векторной функции через производные ее компонент векторы an

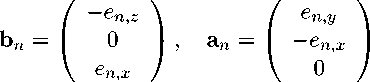
e n,z - e n,y

Теперь можно вычислить постоянные в тетраэдре E , J по формулам (13) и записать подынтегральное выражение квадратичной формы (9) , используя (21) . Мы приведем уже производные этой квадратичной формы (с множителем 1/2, с которым она входит в функционал энергии) по узловым значениям F, P _x , P y , P _z . Например, производные по значениям в первом узле:

e ^∗1 j , a ^∗1 E , b ^∗1 E , c ^∗1 E , (23)

где в последние три выражения не включены члены, получающиеся из квадрата дивергенции P. Они равны соответствующим компонентам вектора e1divP, (24)

где div P выражено через значения линейных функций P x ,P y ,P z в вершинах тетраэдра:

divP = e1(Pi - P4) + e2(P2 - P4) + е3(Рз - P4).(25)

Интегрирование по объему тетраэдра сводится к умножению на его объем, равный смешанному произведению

1 г*[г2 х гз] = h1 hie*[r2 х Г3] = shi,(26)

6               63

где h i — высота, s площадь треугольника со сторонами Г 2 , г з , который будем называть основным. Действительно, вектор [ г 2 х г з ]/2 направлен по нормали к этому треугольнику. Вектор h i e i имеет то же направление и единичный модуль.

• 4    Дискретная модель

Для наглядности полезно иметь дискретную модель, описываемую теми же уравнениями вариационно-разностной схемы. Например, для уравнения Пуассона это электрическая цепь из резисторов, соответствующих отрезкам сетки. Для нашего случая мы построим только аналог для закона сохранения заряда — первого из уравнений (1) .

Для этого продолжим рассмотрение тетраэдра. Построим поверхность, которая отделяет окрестность точки 1 от остальной части тетраэдра. Для этого на каждой боковой поверхности проведем три медианы, которые, как известно, делят эти треугольники на 6 частей с равными площадями. Возьмем какую-либо точку внутри тетраэдра и построим 6 треугольников, в которых она является вершиной, и основаниями – половины построенных медиан, ближайших к точке 1. Получилась искомая поверхность, она состоит из шести треугольников. Спроецируем эту поверхность на основной треугольник. Если проекция точки 1 лежит внутри этого треугольника, получаем фигуру из 6 треугольников. Площадь этой фигуры равны 1/3 площади основного треугольника, поскольку он состоит из трех треугольников — проекций боковых граней, и соотношение площадей при проецировании не изменяется. Если проекция точки 1 лежит вне основного треугольника, проекции одной или двух граней лежат вне него. Соответственно, снаружи оказываются и проекции их частей. Ниже приведем основания включать эти площади со знаком минус. Тогда площадь проекции тоже равна 1/3 площади основного треугольника.

Подставив последнее выражение объема (26) в первое выражение (23) , получаем поток вектора J через построенную поверхность, поскольку вектор e 1 перпендикулярен основному треугольнику и по модулю равен 1/h i . Таким образом, вклад тетраэдра в производную функционала энергии по значению F i есть ток из построенной окрестности вершины 1.

Сложив вклады всех тетраэдров, чьими вершинами является этот узел сетки, получаем полный ток из окрестности узла.

Такова была бы ситуация, если бы во всех узлах сетки значения кусочно-линейных функций F, P x , P y , P z были независимы. Например, если каждую «кубическую» ячейку сетки делить на 5 тетраэдров, 4 из которых отделяют окрестности четырех узлов, связанных диагоналями граней, и пятый — оставшаяся средняя часть ячейки. Мы этого не делаем, поскольку тогда получаются узлы двух видов: одни входят в 8 тетраэдров, другие — в 32. Это также неудобно при использовании блочно-структурированных сеток, поскольку на гранях появляются выделенные диагонали, что требует соседства блоков одинаковой ориентации.

В нашей сетке часть значений кусочно-линейных функций F, P x , P y , P z зависима: в центре «кубической» ячейки — 1/8 суммы значений в ее 8 вершинах, и в центре грани «кубической» ячейки — 1/4 суммы значений в принадлежащей этой грани 4 вершинах «куба». Поэтому токи, полученные при рассмотрении прилегающих тетраэдров в этих точках, распределяются в узлы «кубической» ячейки по правилам дифференцирования сложных функций, то есть из центра «кубической» ячейки с коэффициентами 1/8 во все 8 узлов, и из центров граней с коэффициентами 1/4 в 4 узла этой грани. Подчеркнем, что сами токи из окрестностей зависимых узлов в результате минимизации функционала энергии не определяются, они лишь входят частями в токи из окрестностей узлов «кубической» сетки, которые и получаются равными заданным значениям q j , описанным ниже.

Отметим, что возможен иной выбор как коэффициентов интерполяции, так и самих центров «кубических» ячеек и их граней. Это может быть полезно для сеток с ячейками, сильно отличающихся от параллелепипедов. Мы этот вопрос не рассматривали, поскольку используем довольно правильные сетки, а в параллелепипедах указанный простейший выбор диктуется соображениями симметрии. Заметим также, что описанное деление «кубической» ячейки на 24 тетраэдра, по-видимому, дает кусочно-линейные функции, наиболее близкие к трилинейным. Последние могут быть построены только в параллелепипедах, а наши — в достаточно произвольных ячейках с 8 вершинами.

К сожалению, нам пока не удалось предложить аналогичную дискретную интерпретацию для оставшихся трех выражений (23) в сумме с (24) . Можно только предположить, что это циркуляции вектора E по некоторым контурам в окрестности рассматриваемого узла сетки и поток вектора P через некоторую поверхность, отделяющую окрестность узла от остальной области. Может быть, это даже та же поверхность, через которую мы выше вычислили ток.

Отметим, что в двумерном случае это сделать удалось [3] . Упрощающим обстоятельством для задачи в координатах x, y явилось то, что вектор P имеет только z - компоненту. Поэтому его дивергенция тождественно равна нулю, вычисление x - , y - компонент ротора P не сложнее вычисления градиента F, и rot _z E аналогичен div J .

• 5    Уравнения вариационно-разностной схемы

Продолжим построение уравнений вариационно-разностной схемы, которые являются условиями минимальности функционала энергии, то есть равенством нулю его производных по значениям кусочно-линейных функций F, P _x , P y , P _z в узлах сетки. Вклад отдельного тетраэдра в левую часть уравнения имеет вид суммы (23) и (24) . Правые части уравнений получаются при дифференцировании линейных функционалов W(F, P ) (12) . Каждая из этих производных равна интегралу от одной из функций Q, G _x , G y , G _z с множителем, который в тетраэдре есть линейная функция, равная 1 в рассматриваемом узле и нулю в остальных. Если узел находится на границе, следует добавить интеграл по граничному треугольнику от соответствующей функции из q, g _x , g _y , g _z , тоже с множителем — линейной функцией. Можно считать, что функции изначально заданы значениями этих интегралов. Для гладких функций эти интегралы можно вычислять по простым формулам. Мы считаем функции постоянными в тетраэдрах, умножаем значение на объем тетраэдра и распределяем его поровну в 4 вершины. Аналогично вычисляем интегралы q, g _x , g _y , g _z по граничным треугольникам.

Теперь суммируем вклады всех тетраэдров, чьими вершинами является узел сетки. Среди полученных уравнений есть и уравнения для узлов, в которых F, P x , P y , P z являются линейными комбинациями значений в узлах «кубической» сетки. С этими уравнениями поступаем по правилам дифференцирования сложной функции W(F, P ), то есть добавляем такое уравнение с весами, равными коэффициентам интерполяции F, P _x , P y , P _z к уравнениям в узлах, по которым производится интерполяция. Само уравнение исключается, поскольку среди условий минимума W(F, P ) нет равенства нулю этих производных.

В результате таких вычислений получаем правые и левые части вариационно-разностных уравнений, то есть записываем условия минимума W(F, P ) в виде системы линейных алгебраических уравнений

E j A ij f j = q i , i = 1,...,J. (27)

Элемент Aij сам является матрицей 4*4 соответственно числу неизвестных и уравнений для каждого узла, fj — четверка значений F, Px , Py , Pz в j-том узле, J — полное число узлов сетки. Поскольку в каждое уравнение вовлечено не более 27 узлов, i-тый и его соседи, матрица A — разреженная. В граничных узлах два параметра fj заданы нулевыми в силу главных граничных условий (8). Если участок границы, которому принадлежит данный узел сетки, перпендикулярен одной из осей декартовых координат, то два из значений F, Px , Py , Pz заданы нулевыми в соответствии с (8), и в системе (27) остаются только два из четырех уравнений, полученных аналогично внутренним узлам. В общем случае требуется определить единичные нормальный и касательные к границе векторы и в fj задать нулевыми два коэффициента в разложении по этому базису. Два оставшихся вектора этого базиса используются для построения двух линейных комбинации уравнений, полученных аналогично внутренним узлам, с включением их в (27).

Матрица A, состоящая из блоков A ij , симметрична, так как представляет собой совокупность вторых производных квадратичной формы, ее блоки сопряжены A ij = A _j ^∗ _i , диагональные — симметричны.

Поскольку кусочно-линейные функции F, P принадлежат энергетическому пространству, для них справедливы оценки квадратичной формы (9) сверху и снизу, полученные в работе [11] . В частности, они означают положительную определенность симметричной матрицы A.

Важным параметром матрицы системы линейных алгебраических уравнений является ее число обусловленности, которое для симметричных матриц есть отношение максимального собственного числа к минимальному. В работе [11] доказано, что число обусловленности матрицы A отличается от числа обусловленности аналогичных матриц, возникающих при решении первой и второй краевых задач для уравнения Пуассона, множителем, приблизительно равным параметру неоднородности H (4) , который для D-слоя ионосферы ' 10 ⁶ . Для уравнения Пуассона в той же области минимальное собственное значение, соответствующее самой крупномасштабной гармонике в задаче Неймана, равно 2/R _E ² , где R E = 6400 км – радиус Земли, а наименьшее – 4/км ² , если в D-слое сделать 40 шагов сетки по вертикали. Поэтому число обусловленности порядка 10 ⁸ . Добавив 6 порядков множителя H, получаем 10 ¹⁴ как оценку числа обусловленности матрицы A.

Число обусловленности матрицы приближенно описывает возрастание относительной погрешности решения в сравнении с относительной погрешностью правых частей системы линейных алгебраических уравнений [9]. В частности, при использовании чисел двойной точности, точность которых порядка 10-16 , получаем оценку относительной погрешности решения 0.01. Это не означает, что реальная погрешность будет столь велика, но заставляет подумать об улучшении обусловленности за счет уменьшения горизонтальных размеров расчетной области. Этого можно достичь дополнительной декомпозицией D-слоя всей планеты на его фрагменты с горизонтальными размерами порядка 1000 км. В этом случае число обусловленности уменьшается на два порядка. Именно такая задача будет рассмотрена как пример в следующем параграфе.

В частном случае, когда проводимость σˆ является скаляром σ , функционал энергии W(F, P ) разбивается на независимые функционалы W 1 (F) и W 2 ( P ). Неизвестную функцию F можно сделать равной электрическому потенциалу V , если G = 0. Тогда можно взять P = 0 и минимизировать простой в сравнении с (12) функционал

W 1 (F) =

¹    σ(grad F) ² dΩ - ¹   FQdΩ.

2σ ₀                        σ ₀

Мы используем его для решения задачи электропроводности в атмосфере, то есть в подобласти под ионосферным D-слоем [5] .

• 6    Примеры численного решения

В качестве первого примера рассмотрим задачу Дирихле для системы уравнений (14) в кубе 0 < x < π, 0 < y < π, 0 < z < π. Пусть магнитное поле направлено по оси x и проводимость постоянна. Начнем с проводимости σ _P = 0.1, σ _k = 10, σ H = 0, когда нет гиротропии среды. Чтобы функции F = 0, P _x = sin x sin y sin z , P _y = P _z = 0 были точным решением, зададим правые части Q = 0, G _x = 21 sin x sin y sin z, G _y = 9 cos x cos y sin z, G _z = 9 cos x sin y cos z.

Используем равномерную прямоугольную сетку. В настоящей работе мы представляем только вариационно-разностную схему, не рассматривая способы решения построенной системы линейных алгебраических уравнений (27). Планируется применение многосеточного метода, известного как наиболее эффективный для эллиптических краевых задач. Здесь мы используем метод последовательной верхней релаксации в его блочном варианте, то есть последовательно обходим все узлы сетки, заменяя полученные ранее приближенные значения четверки неизвестных fi на f˜i=fi-τAi-i1(ΣjAijfj-qi).

В силу симметрии и положительной определенности матрицы A такие итерации сходятся при произвольном 0 < τ < 2. При τ = 1 эта итерационная процедура становится методом Зейделя, если к тому же заменить умножение на обратную матрицу A _i ^- _i ¹ делением на диагональные элементы самой A ii . В рассматриваемом случае на сетке с 32 шагами при τ = 1.85 итерации сходятся вшестеро быстрее, чем при τ = 1, и всего вдвое медленнее, чем при таком же решении одного уравнения Пуассона. На крупных сетках выигрыш от τ 6 = 1 существенно меньше.

На рис. 1а показаны разрезы вдоль отрезка y = z = π/2 разностей δPx между приближенными решениями, полученными на сетках с 8, 16 и 32 шагами по каждой переменной, и точным решением. Максимум модуля погрешности убывает в 4.8 и 3.6 раза при таком измельчении сетки, что близко к коэффициенту 4, соответствующего строго квадратичной сходимости приближенных решений к точному решению. Поскольку задача для функции F оказывается независимой, ее погрешность соответствует точности машинных чисел и не превосходит 10-14. Погрешности Py, Pz на сетке с 32 шагами впятеро меньше, чем погрешность Px . Для них тоже видна примерно квадратичная сходимость: убывание максимумов в 3.9 и 3.5 раз.

Рис. 1.

а — разности между приближенными решениями и точным решением задачи 1 δP _x . Число шагов сетки по каждой переменной указано около ломаных.

б — сходимость итерационного процесса на этих же трех сетках, k — номер итерации.

На рис. 1б показана сходимость итерационного процесса на этих же трех сетках. Использована норма невязки, равная сумме модулей невязок всех уравнений (27) :

D=Σ i^J=1 | Σ j A ij f j - q i | . (28)

Начальные значения D близки, поскольку они равны сумме интегралов модулей Gx , Gy , Gz на данной сетке. Уменьшение невязки прекращается по достижении точности машинных чисел. Используя данную в параграфе 3 интерпретацию первого из уравнений вариационно-разностной схемы как тока из окрестности узла сетки, можно пояснить различия уровней насыщения на рис. 1б. При вычислении градиента F и производных Px , Py , Pz погрешность машинного числа делится на шаг сетки h. Потом эти производные умножаются на некоторые геометрические факторы и проводимости, мало зависящие от h. После этого, при вычислении потока, происходит умножение на h2 , тоже с некоторыми геометрическими факторами. Поэтому образуется погрешность, в h раз отличающаяся от машинной точности. Поскольку число узлов возрастает как h-3 , получаем множитель h-2 в значении нормы (28), то есть предельная норма невязки D увеличивается вчетверо при мельчении сетки вдвое. Это и видно на рис. 1б с учетом того, что log 10 (4) ' 0.6. Здесь мы предположили возможность аналогичной интерпретации остальных трех уравнений вариационно-разностной схемы. Этой же интерпретацией объясняется выбор нормы (28): вклад невязок первого из уравнений вариационноразностной схемы в D – это ток, ошибочно перераспределенный между ячейками сетки из-за неточности решения системы (27).

Рассмотрим более сложную задачу в параллелепипеде 0 < x < п, 0 < у < п, 0 < z < п/10, который соответствует высотному интервалу 50-80 км и горизонтальным размерам 300 км. Проводимости зададим характерными для дневной ионосферы над геомагнитным экватором, где магнитное поле горизонтально:

Ст р = i0 ^-10+40z/n , ^ = i0 ^-io+⁶oz/ⁿ , ^ H = q^ - _CT p )_a p .

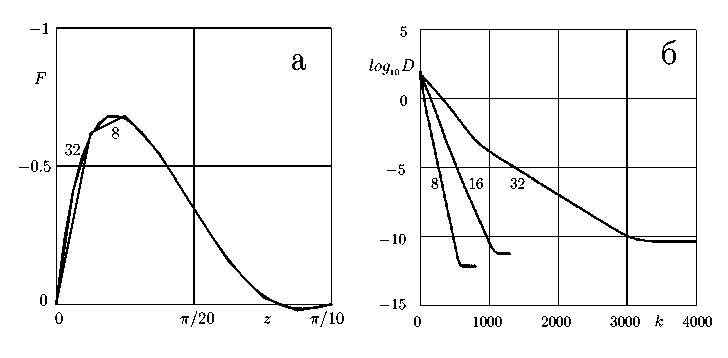
Рис. 2.

а – приближенные решения задачи 2 F . Число шагов сетки по каждой переменной указано около ломаных.

б – сходимость итерационного процесса на этих же трех сетках, k — номер итерации.

Среда гиротропна, и параметр неоднородности H = 106. Правые части зададим в прежнем виде, но сжав в 10 раз по вертикали. Поскольку точное решение не известно, в отличие от рис. 1а на рис. 2а показаны на отрезке x = у = п/2 сами приближенные решения F, полученные на сетках с 8, 16 и 32 шагами по каждой переменной. О квадратичной сходимости к точному решению при уменьшении шага сетки говорить не приходится, поскольку на самой крупной из этих сеток проводимость изменяется впятеро в соседних по высоте ячейках сетки. Тем не менее, видна близость решений в общих точках сетки. Это делает перспективным использование крупных сеток с дальнейшей гладкой интерполяцией, если сами решения гладкие. Сходимость итераций на порядок замедляется по сравнению с первой задачей, и число необходимых итераций стало возрастать как 1/h. Оптимальным оказалось увеличение т = 1.4,1.5,1.7 с мельчением сетки. Следует отметить, что нет необходимости вести итерации до выхода на насыщение. Так, такие же графики на рис. 2а получаются после уменьшения нормы невязки D всего в 1000 раз, то есть достаточно пятой части показанных на рис. 2б итераций.

Заключение

Таким образом, создан вариационно-разностный метод, то есть краевая задача электропроводности сведена к решению системы линейных алгебраических уравнений для узловых значений кусочно-линейных функций, аппроксимирующих решение. Матрица этой системы симметрична и положительно определена. Описан способ приближенной оценки ее числа обусловленности, и оно оценено для задачи электропроводности в D-слое ионосферы Земли. Выведены формулы, необходимые для построения коэффициентов этой матрицы, начиная с геометрических построений в сеточных тетраэдрах. Предложена дискретная модель, позволяющая интерпретировать одно из уравнений вариационно-разностной схемы как закон сохранения заряда, проинтегрированный по ячейкам сетки. На примерах показана сходимость получающихся приближенных решений при мельчении сетки.

Основным достоинством предложенного метода являются симметрия и положительная определенность матрицы полученной системы линейных алгебраических уравнений, что в дальнейшем позволит применить для решения этой системы наиболее эффективные методы. Целесообразно использовать многосеточный метод Федоренко [10] .