Вариационный принцип для сплошных сред, обладающих памятью формы

Сплавы типа нитинола, механическое поведение которых интенсивно изучается в последние десятилетия [1–6], отличаются от большинства металлов тем, что после пластического деформирования силами и последующего нагревания способны восстанавливать первоначальную форму. Термодинамический анализ напряженно-деформированного состояния сплавов с памятью формы требует решения системы дифференциальных уравнений с разрывными функциями, что затрудняет доказательство существования решений в связной задаче термопластичности. В то же время квазистатическое деформирование внешней нагрузкой сплавов типа нитинола при постоянной температуре хорошо описывается феноменологически классической моделью Прандтля–Рейсса с трансляционным упрочнением [2–4], для которой справедлив вариационный принцип типа Рейсснера и доказывается существование обобщенных решений.

По-видимому, нельзя предложить физически приемлемый вариационный принцип, справедливый при произвольных деформациях и температуре. Поэтому цель настоящей работы состоит в том, чтобы отдельно рассмотреть две стадии деформирования сплавов с памятью формы: деформирование силами при постоянной температуре и «обратную деформацию», сопровождающуюся затратами тепла. Каждый из этапов деформирования описывается своим вариационным принципом и для него доказывается существование обобщенных решений.

В разд. 1 приводятся эвристические соображения по формулировке вариационных принципов для материалов с памятью формы без точного определения пространств вводимых функций. Математические определения и доказательства принципов содержатся в разд. 2. Главные трудности при доказательстве теоремы существования на основе вариационного принципа отчетливо проявляются на идеализированной модели, когда отсутствует упрочнение, а гладкая поверхность нагружения заменяется поверхностью Мизеса. Учет указанных факторов не вызывает дополнительных осложнений, в связи с чем эта упрощенная идеально пластическая модель изучается в дальнейшем.

1. Формулировка вариационных принципов. При одноосном растяжении идеально пластических материалов с памятью формы кривые напряжение – деформация зависят от температуры и имеют вид, показанный на рис. 1, T 0 <  T 1 <  Т 2 _Е . Деформирование при «комнатных» температурах Т 0 , Т 1 соответствует поведению идеальных упругопластических материалов с пределами текучести а 0 , а 1 . Если же испытание производится при температуре Т 2 _Е , то наблюдаются две поверхности σ ₁ и σ _{2 ε} на которых прослеживаются большие деформации разных знаков. Остаточная деформация в последнем случае отсутствует. Если а 2 _Е ^ 0, то Т 2 _Е ^ Т 2 и число Т 2 называют температурой восстановления формы.

Кривые на рис. 1 допускают другое толкование. Рассмотрим две стадии деформирования среды. На первой стадии приложим напряжения а < а0 при температуре Т0 . Затем снимем нагрузку и измерим остаточную деформацию ε0 . На втором этапе поднимем температуру до зна- чения T2 без дополнительного нагружения. Образец должен вернуться в первоначальное состояние. Упругопластическое поведение на первом этапе было изучено [7, 8]. Видоизменим изложенное в [7, 8], чтобы результаты стали применимы и ко второму этапу температурных деформаций.

• а) б) в)

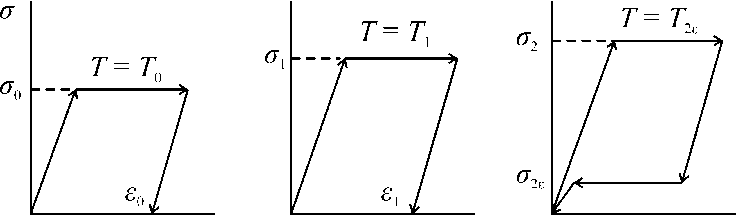
8                   £                     £

Рис. 1

Здесь k – предел текучести материала на сдвиг, s_ij – девиатор напряжений, σ _ij – тензор напряжений, δ _ij – символ Кронекера.

Следуя [9], будем называть тензор напряжений σ _ij допустимым, если его девиатор удовлетворяет соотношению s 2 <  2 k ². Если же девиатор s 0 удовлетворяет неравенству s 0 s 0 <  2 k 0 , k ₀ <  k , то отвечающий ему тензор & 0 назовем безопасным.

Выбираем в качестве определяющих параметров поведения континуума тензор напряжений σ _i и скаляр λ , связанный с тензором скоростей пластической деформации ε _i ^p зависимостью [10]

i zp = ^ - zi, ^e = e^ ki.(2)

Точкой обозначено дифференцирование по времени, ε _ij – тензор скоростей деформаций, E_ijkl – тензор модулей упругости. Тензор λ _{2 ij} возьмем по рекомендации Прагера [11, 12]

Плотность изменения внутренней энергии определим по формуле

U=Eijkl+i,(4)

Формальная свертка этого выражения с тензором σ _ij приводит к равенствам

^U = & j £ j ’ ^U = E ijkl & ij & kl + & ij ^z ij , а интеграл от последнего выражения по объему и времени равносилен первому началу термодинамики, если нет притока тепла ( q & = 0).

Таким образом, если принять закон Прандтля–Рейсса в качестве определяющего соотношения, то для внутренней энергии имеем выражение (4), где i = & j s Р .

Тот же результат получается, если формально потребовать выполнения соотношений (2)–(4) и вывести из законов термодинамики правило разделения деформации на упругую и пластическую части. Действительно, из первого начала термодинамики при q & = 0 следует

U = & ij ^£ ij = ^{E -} kl & ij & kl ⁺ j ,                               ⁽⁵⁾

что равносильно разделению деформации на упругую и пластическую части:

e gpp-

^ε ij ^ε ij ^ε ijijkl ^σ kl ^ε ij ^.

Наконец, примем постулат Друкера о нормальности вектора ε _i ^p _j к поверхности нагружения (1) и найдем [13]

tf = ^psij , 4 = 0-

Подставляя выражения (7) в условие (1), определим параметр λ _p и девиатор s_ij

AP= sjsj/2k2, stJ = k 2^ (sjsjГ1/2.(8)

Выражение для скорости изменения плотности внутренней энергии преобразуется к виду

U = f + h, f = E-^k, h = k ^(sj sj )12.(9)

Таким образом, постулируя соотношения (3), (4), обнаруживаем не только разделение деформации на обратимую и необратимую части, но и автоматическое выполнение первого начала термодинамики при изотермической деформации сплошной среды без притока тепла. Второе начало термодинамики также выполняется автоматически, поскольку выражение f можно отождествить со скоростью изменения свободной энергии Гельмгольца, а отсутствие подводимого тепла ( q & = 0) и выражение (9) дают соотношение

0 = q & <  Ts & = h , где T – температура, а s & – скорость изменения энтропии, объединяющее в одной формуле два основных закона термодинамики при изотермическом нагружении, как это отражено в формулах (29), (30) работы [10].

В итоге получается, что постановка задачи изотермического деформирования упругопластических тел в окончательном виде не содержит ни температуры, ни законов термодинамики. Остается невыясненным, как преобразуется «скрытая теплота пластического плавления» h . Подразумевается, что эта часть энергии рассеивается в окружающую среду. Последний процесс протекает столь быстро (или деформация настолько медленная), что основные параметры течения не меняются. Именно такие процессы изучаются далее.

Аналогия между пластическим течением при постоянной температуре и плавлением была замечена Борном и Фюртом [14] – оба явления сопровождаются рассеянием внутренней (скрытой) энергии в окружающую среду. Формула (4), так же как уравнения Прандля–Рейсса, обеспечивает конкретный механизм рассеяния: вначале при постоянной температуре работа внешних сил преобразуется во внутреннюю энергию образца; последняя затем рассеивается во внешнее пространство с коэффициентом теплопроводности, равным бесконечности.

Пусть на упругопластическое тело, занимающее область D с границей д D = д D u + д D_p , действует система объемных сил X i , причем на поверхности д D u равны нулю скорости, а на д D_p -поверхностные силы. Интервал времени, в течение которого происходит деформирование, обозначим [0, t ]. Предположим, что в любой момент времени найдется безопасное статически допустимое распределение напряжений σ _i ⁰ _j , когда при любых скоростях v_i имеет место равенство

J jj dx - J Xvdx = 0.                           ⁽¹⁰⁾

DD

Задача об упругопластическом поведении среды состоит в нахождении таких тензора σij и вектора vi , чтобы для функции состояния U (σij,εijp ) (9) при любых σij выполнялись соотноше- ние (5) и уравнения (1), (7). Внутренний параметр λ определяется из равенств (2), (3), а вектор нагрузки Xi удовлетворяет равенству (10).

Было показано [7, 8], что сформулированная задача равносильна нахождению седловой точки функции Лагранжа

L ( P j , ^v i ) = ¹ J E -^ ij ^ kl d^{V +} J ^{( P 0}

s ij - P & j S j ) dV , dV = dx 1 dx ₂ dx₃dt ,

² D x [0, t ]                        D x [0, t ]

на множестве произвольных скоростей v i и девиаторов s² <  2 k ².

Если справедливо соотношение (10), то обобщенное решение (11) существует. Из этого факта вытекает выполнение равенства (6) и первого начала термодинамики в форме (5). Поскольку Л > 0, то справедливо второе начало термодинамики в форме неравенства Клаузиуса-Дюгема q < ts ,                                                   (12)

так как в отсутствие внешнего теплового потока ( q & = 0) скорость изменения внутренней энергии может быть представлена в виде

Механический смысл существования седловой точки в сплошной среде состоит в следующем. До тех пор пока нагрузка такова, что можно указать в любой точке тела допустимый тензор 0

σ _ij , решение существует.

Снизим нагрузку σ _i ⁰ _j до значения ε ₀ σ _i ⁰ _j , где ε ₀ – малое число. Пусть напряженному состоянию в точке x_i , испытывающей при нагрузке σ _i ⁰ _j пластические деформации, отвечает в пространстве напряжений тензор A, а при нагрузке ε ₀ σ _i ⁰ _j – тензор B (рис. 2). Нагреем тело до температуры T _{2 ε} (рис. 1,в).

Рассмотрим девятимерное многообразие R , ограниченное поверхностями { S : si = 2 k 2} и { S _s : s i = 2 s²k 2}. Поверхность S _ε – это результат подобного преобразования поверхности S с малым числом ε . Назовем тензор σ _ij допустимым, если выполнено включение C j с R (рис. 3). Тензор у будем считать безопасным, если имеет место включение с- с R 0 . Многообразие R 0 с R , ограничено поверхностями { S ⁰ : s i = 2 к 02 } и { S 0 : s i = 2 s 1 k 2 }, а входящие в определения поверхностей постоянные удовлетворяют неравенствам ^к 02 <  ^к2 , ^S 1 >  ^S •

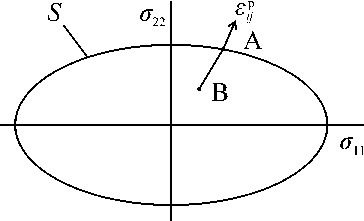
Рис. 2

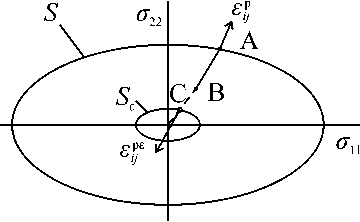
Рис. 3

возможна пластическая деформация sjs = -s j в силу подобия поверхностей S и Ss . Ясно, что приведенное рассуждение справедливо при отказе от постулата Друкера в первоначальной форме ((aj - су i*• )s j > 0 , где сj - действительное, ст J - любое возможное поле напряжений) и исполь зовании его локального следствия стjS j = 0 (либо условия Циглера об ортогональности термодинамических сил и потоков). Такой подход часто применяют в задачах термопластичности [15].

В качестве внутренних параметров среды выбираем тензор напряжений σij и работу χ , необходимую для «обратного» превращения [1, 2]. В соотношении (2) примем по аналогии с рис. 1,в тензор Л2j = у , где у - тензор напряжений в точке A (рис. 3). На поверхности Ss будем иметь равенство (9) при замене h на h 2 = к2^(8^ sip )1/2,                                      (13)

Выражения (10) и (12) записываются в прежней форме.

Таким образом, имеем следующую аналогию: различие процессов деформирования материала с памятью формы (когда q & = 0) и «обратного теплового деформирования» в отсутствие сил в рамках механики сплошной среды заключается лишь в знаке ε _ii ^p . Поскольку в обоих случаях внутренняя энергия зависит только от σ _ij и ε _i ^p _i , в формуле для внутренней энергии (9) или (13) изменяется только коэффициент k . Роль «скрытой теплоты пластического плавления» h при обратной тепловой деформации выполняет «скрытая теплота обратного превращения» h ₂ , а в первом начале термодинамики («при обратной деформации в отсутствие сил») скорость работы внешних сил σ _ij ε _ij заменяется скоростью подвода тепла q & .

Поэтому на этапе теплового деформирования надо найти тензор скоростей изменения напряжений σ & _ij и вектор скоростей v_i , такие, чтобы на допустимом множестве девиаторов s_ij выполнялось равенство (14) и существовала седловая точка функции Лагранжа (11), в которой ве-личина σ _i ⁰ _j заменена на ε ₀ σ _i ⁰ _j .

В такой форме вариационный принцип будет доказан в следующем разделе. Затем устанавливается возможность перехода к пределу, когда е ^ 0.

По сути, метод доказательства существования решений эквивалентен введению малой вязкости в задачи жесткопластического течения, а вариационный принцип является видоизменением общих теорем в теории упругопластичности [16, 17].

• 2.    Доказательство вариационного принципа. Переходим к математически строгой формулировке задачи. Пусть среда занимает трехмерную область D с границей д D = д D u + д D p . На части границы д D u задан вектор скоростей v i , а на д D p известен тензор скоростей напряжений с т ij . Будем изучать задачу на интервале времени [0, t ]. Определим четырехмерную область M = D х [0, t ] с границей

д M = дM_u +дМ_п , д M_u = д D_u х [0, t ], дМ_п =д D_n х [0, t ]. upuu   pp

Введем гильбертово пространство функций H как пополнение дифференцируемых по времени тензоров σ _ij в норме, определяемой скалярным произведением

M и пространство возможных скоростей как множество мер с нормой

IIvilU(M) = miax{ j £ij(vi,dm) + J I £ij(vi,dm) I},

’j M+ где принято M = M+ + M- , причем подобласти M+ и M- разбивают область M так, что внутри M+ знак eij положителен, а внутри M- отрицателен.

Пространство ограниченных деформаций BD ( M ) получается пополнением множества функций

2sij (vi, dm) = (д vi /XXj + д Vj /дxi) dm по норме (16). Это пространство не является рефлексивным, оно изучалось в связи с задачами вязкопластичности [7, 18]. В частности, доказано, что функции из BD(M) имеют след на кусочно-гладкой поверхности дDu , принадлежащий пространству интегрируемых функций [18]. Это позволяет записать следующее условие неподвижности границы дMu :

II <,( M ) = ⁰ .                                           < ¹⁷⁾

Отсутствие напряжений на ∂ M_p запишем в виде

I σ ij ( ∂ M p ) _L ∞ _{( M )} = 0.                                           (18)

Здесь L ^∞ ( M ) – пространство ограниченных измеримых функций на множестве M .

Выделим в пространствах H и BD ( M ) множества σ _ij и v_i так, чтобы выполнялись условия (17), (18) и следующие соотношения (всюду далее, если не оговорено иное, интегрирование ведется по области M ) :

R={σij:σij∈L∞(M),2ε2k22≤si2j≤2k22,sij=σij-σkkδij/3,(19)

Условие (19) означает, что рассматриваются лишь допустимые напряженные состояния (рис. 3), а соотношения (20) и (21) – это первый и второй законы термодинамики.

Пусть, наконец, к телу приложена нагрузка, которая может быть уравновешена безопасным тензором напряжений σ _i ⁰ _j , и

2 ε ₁ k ₂ < s_ijs_ij <  2 k ₀₂ , s_ij = σ _ij - σ _kk δ _ij /3, k ₀₂ < k ₂, ε ₁ >  ε .

и докажем, что на множестве R × BD ( M ) с условиями (17)–(21) существуют σ _ij , v_i , которые соответствуют седловой точке функции Лагранжа L ( σ _ij , v_i ).

Доказательство состоит в проверке выполнения условий приводимой ниже теоремы [19]: если для множеств с ограничениями (15)–(22) существует элемент v ₀ ∈ BD ( M ), такой, что

и выполняется соотношение liminfL(σij,vi)=-∞, vi ∈ BD(M), σij ∈ R, II vi IIBD(M)→∞,(25)

то функционал L ( σ _ij , v_i ) имеет на R × BD ( M ) седловую точку

L(σij,vi)=minsupL(σi′j,vi′)=maxinfL(σi′j,vi′)=m0 ,(26)

σi′j∈R vi′∈BD(M)               vi′∈BD(M) σi′j∈R и среди σi′j, vi′ можно выбрать подпоследовательность, такую, что σi′j →σij слабо в H , а vi′ →vi слабо* в BD(M).

^σ ij ^{∈ R}

Здесь c , c ₁ – некоторые постоянные. Неравенство (27) влечет выполнение соотношения (25), и смешанный вариационный принцип обоснован.

Если σ _ij и v_i – дифференцируемые по координатам и времени функции, то в равенстве (23) можно заменить область M на D и убедиться в справедливости закона Прандтля–Рейсса. В самом деле, вариацию L ( σ _ij , v_i ) представим в форме

D

Вследствие произвольности ( σ _ij - σ _i ′ _j ) везде, кроме точек поверхности

Φ = si2j -2k22ε2=0,(29)

можно записать равенство

представляющее собой закон Прандтля–Рейсса, из которого следует, что для гладких функций, отвечающих течению на поверхности (29), соотношение (20) принимает вид

∫ q & dm = ∫ ((1 - ε ) k ₂V2( ε ij ^p ε i ^p j )^1/2) dm .

Интеграл в правой части написанной формулы неотрицателен, поэтому приток тепла имеет направленный характер, и второе начало термодинамики становится следствием первого.

Равенство (30) указывает также на возможность замены в условии текучести (1) поверхности (29) любой другой гладкой поверхностью Φ ( s_ij ) = 0. В формулах (8) нужно заменить s_ij на 1

∂Φ ∂ s_ij , а вместо выражения ( ε _i ^p _j ε _i ^p _j )² подставить диссипативный потенциал, являющийся преобразованием Лежандра функции Φ .

Рассмотрим последовательность σ _i ^ε _j , v_i ^ε , когда ε → 0 в условии (19). Так как величина max I ^σ i ^ε j II в силу условия (19) ограничена, то при любом ε ограничен интеграл

U_p = ∫ ( ε _ij ^p ε _ij ^p )^1/2 dm .

Следовательно, при ε → 0 [20] из последовательности v_i ^ε можно выбрать подпоследовательность, которая слабо* стремится к некоторому пределу в BD ( M ), его можно принять за решение задачи об «обратном течении» сплавов с памятью формы при температуре T ₂ .

Разумеется, в предельном состоянии не справедлив вариационный принцип, так как в наиболее важном частном случае σ _ij → 0 «пропадают» два первых члена подынтегрального выражения в правой части соотношения (20). Первый закон термодинамики превращается в очевидное равенство, которое описывает одномерное течение, поскольку «запоминается» лишь второй инвариант тензора ε _i ^p _j .

Отметим также, что для преобразования условия экстремальности функции Лагранжа к форме (28) требуется доказательство регулярности тензора σ _ij и вектора v_i . Эта задача исследовалась многими авторами, но еще далека от решения [21].