Variations of structure modeling methods and Raman spectral characteristics for the iodine crystal

Structure-forming non-covalent interactions of halogens Hal…Hal in crystals and solid states in many ways determine thermodynamic, thermophysical, spectral and other properties [1, 2]. It is known that because of anisotropy of electrostatic potential on the Van der Waals surfaces of a molecule, the halogen atom, bound in the molecule, can form two types of non-covalent interactions [3, 4]. The Type I interactions are purely Van der Waals interactions in their nature; they are characterized by random positioning of two covalent bonds of halogens, belonging to different molecules. The Type II interactions are strongly directed. They are noted for mutual orientation of molecules, in which two covalent bonds of halogens are situated at the right angle to each other. In this case the area of electron density accumulation in one halogen atom is directed to the area of electron density depletion in the other atom. This area of electron density depletion is always formed on the extension of the covalent bond of a halogen atom; it is called σ-hole [5]. In this area the nucleus is shielded by valence electrons to a lesser degree, and the area of generally positive values of electrostatic potential is formed [6, 7]. This type of non-covalent interactions is called halogen bonds [8, 9].

Halogen bond properties can be successfully studied from the perspective of QTAIMC – Quantum Theory of Atoms in Molecules and Crystals [10], because this theory is aimed at searching for binding interactions, including those which occur among non-covalent ones. Such interactions are characterized by bond paths: two lines, each point of which is different from other neighboring points of space by larger values of electron density. These lines connect atomic nuclei, which are separated by the general interatomic surface, where through the vector gradient of electron density equals zero. The QTAIMC approach includes the topological analysis of electron density ρ( r ), obtained by quantum-chemical calculations, or within precise X-ray diffraction experiment. In its turn the topological analysis allows us to identify critical points of electron density. The electron density and its properties in the bond critical points are important characteristic values describing chemical bond properties in molecules and crystals.

Halogen bonds in a chlorine crystal were first described from the perspective of electron density distribution properties, obtained through high-resolution X-ray diffraction experiment [11]. The paper

Физическая химия presents the visual presentation of mutually consistent orientation of the exhaustion area on to the area of electron accumulation with the Laplacian of electron density ∇2ρ(r). The Laplacian of electron density characterizes three-dimensional curvature of its dropping with increase of distance from the atom nucleus. Depending on the ratio of radial positive curvature of electron density and the curvature in the orthogonal directions, the Laplacian will alternate in signs. Alternating minimums and maximums of ∇2ρ(r) correspond to areas of accumulation ∇2ρ(r)<0 and depletion ∇2ρ(r)>0 of the electron density around the nucleus, so they show atom electron shells. However, ranges of the Laplacian negative values, which should correspond to outermost electron shells, do not appear at atomic numbers Z > 29, as it is specified in the paper [12]. That is why, as a rule, other functions of electron density, for instance, one-electron potential, are used for the Br and I compounds for the sake of outermost electron shells localization [9, 13].

Another important feature at reproduction of some experimentally observed properties of halogens with high atomic numbers, such as I or Аt, is the importance of relativistic effect, this is particularly manifested when analyzing properties, connected with outermost electron shells [14, 15]. Together with structural information, obtained from the electron density distribution analysis in the iodine crystal, the special attention shall be paid to its vibrational properties. The most informative method in studying I–I covalent bonds in crystals and solids is Raman spectroscopy [16, 17]. A great number of works deal with the theoretical frequency rates, obtained for structures of isolated polyiodide anions or cationanions systems [18, 19]. However, this approach does not allow us to take into consideration the influence of crystal environment, effects of intermolecular interactions in solids, that makes it difficult to compare with the experimental spectral data. Such differences can be partly due to significant disturbance of isolated structure geometry of a molecular complex or a cluster in comparison with the crystal structure. The dynamic approach to crystal lattice with consideration of atomic vibrations around equilibrium positions allows us to explain physicochemical crystal properties, connected with thermal effects, phase transitions, conduction properties. Theoretical calculations allow us to deduce vibrational spectra, to forecast crystal structure stability and to obtain thermodynamic properties, such as heat of formation and sublimation, entropy, and others [20].

The purpose of this paper is to select basis sets, allowing to provide the accurate modeling of covalent and halogen bonds and their characteristics in the iodine crystal, as well as to calculate wavenumbers for vibrations, that are active in Raman spectra. The method should provide data, suitable for the topological analysis of electron density in conditions of periodic quantum-chemical calculations, and should reproduce experimental data as accurately as possible. For this purpose several of basis sets for the iodine atom available in literature have been tested in this paper, and possibilities and advantages of the two approaches to relativistic effect consideration have been compared. These two approaches are: usage of Effective Core Pseudopotentials and the Gaussian-type basis set, constructed according to Douglas-Kroll-Hess approach [21, 22]. We make the comparison of calculated geometric characteristics of the iodine crystal structure and of electron density properties, calculated for covalent and halogen bonds, with the data obtained on the basis of the high resolution X-ray diffraction experiment [23]. Theoretical vibrational characteristics are compared to the experimental polarized Raman spectra for the single crystal of iodine [24].

Calculations

As a part of the study the periodic calculations of the wave function in the iodine crystal were made using the program CRYSTAL14, by the Kohn-Sham method (B3LYP) and various basis sets, shown in Table 1. Two groups of basis sets were tested. One group included Stuttgart fully-relativistic energy-consistent pseudopotentials ECP-mdf28 and ECP-mdf46 including 28 and 46 core electrons, respectively [25]. The pseudopotential ECP-mdf28 could be attributed to the group of potentials with the small core, and ECP-mdf46 had the member of the group with the large core. When using the pseudopotential ECP-mdf46 only outer-shell electrons 5s2 и 5p5 were included into the valence part. The valence part in both cases was described by the three-time split basis sets of the VTZ type. The other group was represented by the DZVP basis set, including 14 shells [26] and its analogue DZVPmod including 11 shells [27]. In the DZVPmod basis set the sp-type hybrid shells were used to describe internal electron levels, so that up to 8 electrons that could be situated existed in that shell. Accounting of relativistic effect was implemented with the help of the DZPDKH basis set in terms of the Douglas-Kroll-Hess ap- proach [21, 22]. The basis set was obtained through optimization of standard Gaussian function coefficients [28, 29], approximating equations, obtained from the electronic part of Dirac Hamiltonian [30].

Iodine crystal structure optimization was made for all atoms of the irreducible cell part with fixed cell parameters. Allowed atom coordinate variations were only those, which did not cause changes in the crystal symmetry. The Hessian matrix was calculated for the found optimal atom configuration at the Γ point in the center of the Brillouin zone. Vibration frequencies were calculated at the Γ point in the harmonic approximation. On the basis of the obtained data the total Raman intensities were calculated for the single crystal of iodine.

Results and Discussion

Mutual arrangement of molecules with halogen bonds in the iodine crystal and with the interatomic distances, stated in the paper [23], is shown in Fig. 1. It has been found that in the case of using fully-relativistic core pseudopotentials ECP-mdf28 and the valence part, described by the VTZ basis set, such geometric characteristics, as the covalent and halogen bond lengths, are reproduced most accurately: Δ R I-I = 0.04 Å, Δ R I…I = -0.03 Å, where Δ R= R ^calculated – R ^experimental. According to the data, represented in Table 1, other basis sets also show satisfactory results when localizing equilibrium geometry in the crystal. In all considered cases the positive values of Δ R I-I have been observed, besides, the I…I halogen bond lengths have been underestimated in most of the cases.

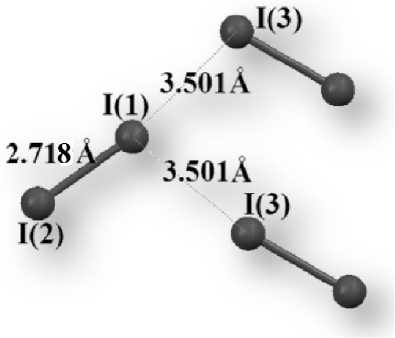
Fig. 1. Mutual arrangement of molecules with halogen bonds in the iodine crystal

Table 1

Distances (Å), the values of the electron density in the bond critical point (a.u.) in the crystal structure of iodine, optimized in different basis sets

Basis set	I(1)–I(2) Covalent bond		I(1)…I(3) Halogen bond		I(1)…I(1) Van der Waals interactions
	R calculation	ρ( r b )	R calculation	ρ( r b )	R calculation	ρ( r b )
ECP-mdf46 VTZ	2.876	0.045	3.709	0.011	-	-
ECP-mdf28 VTZ	2.755	0.059	3.474	0.018	3.977	0.008
DZVPmod	2.791	0.062	3.473	0.018	3.940	0.009
DZVP	2.802	0.061	3.467	0.019	3.939	0.009
DZPDKH	2.812	0.060	3.414	0.022	4.060	0.007
Experimental [23]	Rexp =2.718 ρ( r b )exp=0.050		Rexp =3.501 ρ( r b )exp =0.015		Rexp =3.980 ρ( r b )exp =0.009

The results of the theoretical topological analysis of electron density have been compared to the data from the paper [23]. There the adjusted values of electron density restored on the basis of the extended multipole modeling Hansen and Coppens approach [31] have been analyzed for I-I covalent bonds and the strongest I…I noncovalent interactions. The application of basis sets with core pseudopo-

Физическая химия tentials leads to underestimation (ECP-mdf46 VTZ) and overestimation (ECP-mdf28 VTZ) of electron density in the I-I covalent bond critical points. The DZPDKH basis set provides a significantly underestimated halogen bond length and, consequently, an overestimated electron density in the halogen bond critical points Δρ(rb) = 0.007 atomic units. However, the observed range of Δρ(rb) values both for covalent and halogen bonds may be considered to be reasonable.

The following characteristic features have been observed while analyzing the Laplacian of electron density distribution in the crystal plane, containing halogen bonds between diiodine molecules. When using the DZVP basis sets with core pseudopotentials, the covalent bond area and the space between neighbouring molecules are described in the similar way. In both cases the covalent bond areas have similar level of observed details. However, the Laplacian of electron density in Fig. 2a,b does not show the electron density accumulation in the outermost electron shell area of iodine. This fact evidences low informative value of the ∇ ² ρ ( r ) function when describing iodine ability to form halogen bonds. On the contrary, the outline map of the electron density Laplacian, obtained through the DZPDKH basis set and indicated in Figure 2c demonstrates the electron density accumulation in the iodine atom equatorial area and exhaustion formed on the continuation of the covalent bond. Consequently, the DZPDKH basis set appears to be the only one of the studied sets, which demonstrates the principle of halogen bond formation: orientation of the area of electron density accumulation of one atom up on the area of electron density exhaustion of the other. Figure 2c shows the I-I covalent bond area in greater details (contour lines of 0.002, 0.004 and 0.008 atomic units) and it also has the contour line of 0.002 atomic units in the halogen bond area unlike Fig. 2a and 2b.

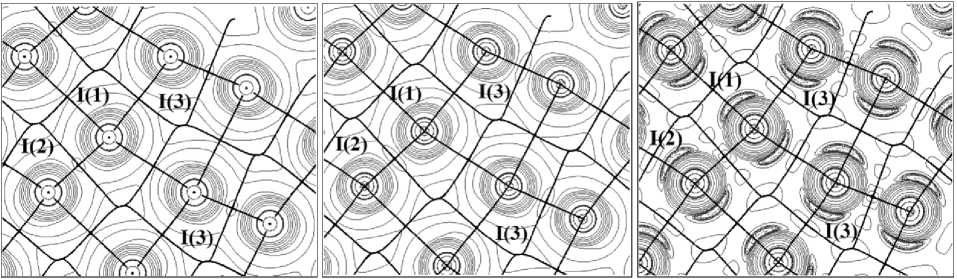
а)                                            b)                                         c)

Fig. 2. The contour lines of the Laplacian of the electron density, accompanied by bond paths in iodine crystal in a variety of basis sets: in fully-relativistic pseudopotential basis set type ECP-28mdf VTZ (a), in the DZVP basis set (b) and DZPDKH (c)

According to the data of experimental polarized spectra [24], two lines are observed for the iodine crystal. These lines correspond to the in-phase and out-of-phase valence symmetrical vibrations. In the first case, the change of lengths of neighboring molecules is in coordination, while in the second case, it is out of phase: the stretch of the covalent bond in one molecule corresponds to the contraction in the neighboring molecule. Symmetry of obtained in-phase A g and out-of-phase B 2g vibrations corresponds to the experimental data from the polarized spectra [24] (Table 2).

Table 2

The wavenumbers of valence vibrations in the crystal of iodine calculated using a variety of basis sets

Basis set	υ (A g ) I–I, cm-1	υ (B 2g ) I–I, cm-1
ECP-mdf46 VTZ	166.5	177.5
ECP-mdf28 VTZ	196.5	202.2
DZVPmod	178.6	187.4
DZVP	180.7	188.5
DZPDKH	180.5	188.8
Experimental [25]	180	189

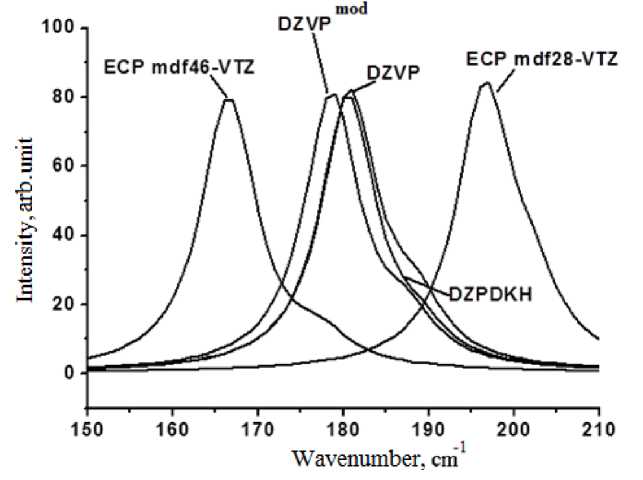
Fig. 3. Calculated unpolarized Raman spectra of iodine crystal optimized in various basis sets

On the basis of obtained theoretical wavenumbers for stretching vibrations in the iodine crystal it is possible to select a group of preferable basis sets, reproducing the data of experimental polarized spectra within the error of 2 cm-1. They are DZVPmod, DZVP and DZPDKH. The application of the core pseudopotential with a big core ECP-mdf46 leads to substantial decrease of obtained wavenumbers, and application of the pseudopotential with a small core ECP-mdf28 leads to underestimation, where deviations from the experimental value in these cases are comparable.

Display of the calculated integrated Raman spectra (Fig. 3) allows us to visually assess the ratio of in-phase and out-of-phase vibrations and overlapping of the lines, corresponding to them. Maximum resolution of lines is attained through the use of the basis set ECP-mdf46 VTZ, the difference between stretching peaks equals 13 cm-1. The greatest overlapping of lines is observed in the basis set ECP-mdf28 VTZ, where the difference between stretching peaks equals 6 cm-1. Basis sets of the DZVP group demonstrate roughly the same difference between wavenumbers of in-phase and out-of-phase vibrations; however, in case of the DZPDKH basis the out-of-phase vibration is characterized by relatively lower intensity.

Conclusion

As can be seen from the above, basis sets with fully-relativistic core pseudopotentials slightly underestimate electron density in the critical point of the covalent bond. However, lack of overlapping in grade lines in the area linking to the core makes it vulnerable to apply basis sets with core pseudopotentials in the electron density topological analysis tasks.

Calculated wavenumbers of iodine vibrations in the crystal, which have been obtained when analyzing the basis sets, show that the application of core pseudopotentials ECP-mdf46 and ECP-mdf28 leads to significant deviations from experimentally observed values. Other basis sets reproduce experimentally observed wavenumbers within the accuracy up to ±2 cm–1, only underestimating the difference between in-phase and out-of-phase vibrations a little.

The Laplacian of electron density, obtained with the use of the DZPDKH basis set, demonstrates accumulation of electron density in the area of the outermost valence shell of iodine atoms. That is why the DZPDKH basis set, where the relativistic effect on the basis of the Douglas-Kroll-Hess approach is taken into consideration, is the most suitable for modeling and analyzing electron density topological properties in crystals of iodine containing compounds with halogen bonds.

The work was supported by the Russian Ministry for Education and Science GZ729, and was carried out on a supercomputer "TORNADO" SUSU.

Физическая химия