Various Approaches of Community Detection in Complex Networks: A Glance

Published Online April 2016 in MECS

Real graphs are not same as homogenous random graphs. Both very high and very low degrees exist in these networks. In these networks, the nodes differ in their degree distribution globally and the edges differ in their distribution locally. It has been seen that in a particular group of nodes the local distribution of edges is more than network’s global distribution [2]. Most of world networks that exist are represented with vertices and edges in which vertices represent the systems and edges represent the relationship between the vertices. Some examples of the networks that exist are Facebook, Google, twitter and LinkedIn etc [4]. The communities that exist in different networks show the existence of networks structure. These communities are the nodes groups in which different nodes are found constituting different community structures.

Communities have an important role in understanding a network. Communities are basically those that form group of nodes that are strongly interconnected sharing many common features. Communities mostly arises in the social networks where different individual with common properties based on different kinds of relationship like family, school, friends, works and sports etc. form random groups [9]. The determination of communities in different networks has various advantages. It can disclose surprising behaviors. For example India is divided into various regions on the basis of different languages. Community detection problem has applications beyond the analysis of social behaviors e.g. in metabolic networks, in image processing and criminal networks etc.

In graph theory and computer science, community detection is closely related to graph partitioning and in sociology, it is related to hierarchical clustering. Graph partitioning basically determines the group of nodes that on average are more similar to each other than the rest of network [7]. The main formulation of the problem of partitioning is to define a cut like minimum cut- the cut identifying the minimal set of edges that bisects the graph and the maximum cut- the cut identifying the maximal set of edges that bisects the graph. Different techniques have been used for clustering. In data clustering, instead of grouping items on the basis of relationship, grouping is done on the basis of their attributes [12]. Two types of concepts are used in data clustering with one as similarity and another as distance. In distance based clustering technique like K-means clustering, the clustering of data points is done on the basis of minimization of intracluster sum of squared distances.

Community structures in real world are mostly having nested structure. Therefore these structures can be modelled as a dendrogram. The hierarchical clustering technique is that which discover natural divisions of different networks into groups by producing dendrogram as an output. The dendrogram is basically a chain of partitions in which each partition is finer than the next [5]. Hierarchical clustering has been further categorized into two techniques. One is Agglomerative in which all the nodes are represented as different clusters and the two clusters are merged on similarity basis [3]. Other one is Divisive clustering in which clustering starts with representing all nodes as a one big cluster and the cluster is divided into two divisions on the basis of similarity. The process continues till every node is in a cluster by itself. In spectral graph clustering, partitioning of data points is done on the basis of similarity of eigenvectors of matrix [6]. The eigenvectors are clustered either by K- means clustering or hierarchical clustering technique. In correlation clustering problem, the real valued edge weights are considered that are positive values. These edge weights determine the level of confidence of clustering two end points [7]. Correlation clustering can be done either by maximizing or minimizing the sum of intra-cluster edge weights.

• II.    Literature Survey

In recent years, many authors have given their contributions in the field of community detection to detect communities in complex networks. The literature survey has been divided into two categories i.e. community detection on the basis of analytical and evolutionary approaches.

• A.    Analytical Approaches

Ester et al. [1] proposed a method based on the clustering in large spatial databases with noise named as DBSCAN. The input parameter requirement in this method is only one. Authors had tested their method on synthetic as well as real data. The results showed the effectiveness and accuracy of DBSCAN.

Girvan and Newman [2] proposed Edge-betweenness based divisive algorithms for detecting communities in large networks. The authors used the concept of edgebetweenness determining the edge importance in connecting the nodes via shortest paths. The algorithm first computes the betweenness of all edges and then removes the edge with high edge-betweenness, one at a time until the graph disconnected. The whole process is repeated until there are no more edges.

Arenas et al. [3] proposed multiple resolution modular structure screening method which is based on modularity optimization. Authors tested their method on synthetic as well as real social networks and succeeded in finding the exact splitting of real social networks.

Blondel et al. [4] proposed a greedy hierarchical clustering algorithm named as Louvain method. The objective function considered in this algorithm was modularity. The algorithm is divided into two phases, with one as optimization phase and other one as aggregation phase. In optimization phase, the individual nodes are treated as individual communities and on the basis of modularity optimal partitioning is done i.e. the individual nodes which are considered as individual communities are removed from their current and placed into their neighbour communities with highest modularity value. This phase is considered till there is no community with non-negative value. In aggregation phase, the communities formed after optimization phase is considered as input i.e. the communities formed after optimization is considered as individual communities and again the optimization is applied on these communities thus by improving the modularity function by making the community of group of nodes instead of individual nodes.

Lancichinetti et al. [5] proposed the first algorithm that detects both overlapping communities as well as hierarchical structure based on the local fitness measure objective function. Authors tested their algorithm on both real and artificial world networks and produces excellent results.

Huang et al. [6] proposed a greedy algorithm based on criterion named as similarity based tightness and they named the algorithm as LTE (Local Tightness Expansion). The authors used this algorithm on both overlapping as well as non-overlapping communities and also showed that the algorithm is efficient in speed and has scalability when used for detection in large scale networks. Authors had also performed experiments on real world and synthetic data sets and produces good results.

Saha et al. [7] proposed an approach based on fuzzy clustering. They applied the approach for detection of communities on weighted graphs. So, the authors named their approach as FCWG (Fuzzy Clustering for Weighted Graphs). Authors used their approach for both social as well as biological networks.

• E. Griechisch and A. Pluhar [8] proposed a method based on extension of modularity and fuzzy partitioning. They also applied their method for detection of overlapping communities and produces better results but their method takes some time in determination of optimal modularity value.

Erwan Le Martelot and Chris Hankin [9] [10] proposed a new method which is based on two criteria one is global and other is local. Global criterion algorithm is almost similar to Louvain method but it has one advantage over latter that it can be applied for multiscale detection of communities. Like Louvain this algorithm also have two phases. In first phase, the individual nodes are treated as individual communities and on the basis of modularity grouping of one with its respective neighbor community is done. In second merging phase, the communities formed in first phase are taken as input and merging of those communities further takes place in order to improving the modularity value. Local criteria algorithm is used in overlapping communities. The first phase is similar to global criteria but the second phase is not compulsory in this criterion until the overlapping of communities is more than half i.e. merging of communities is done only if communities significantly overlap.

• B.    Evolutionary Approaches

Handl and Knowles [11] proposed an evolutionary approach based on Multiobjective clustering of a network with automatic cluster determination and named it as MOCK (Multiobjective Optimization of Clusters with automatic K determination). Authors compared their approach with single objective clustering problem and observed that MOCK is more efficient in optimizing the individual objectives.

Xiadong et al. [12] proposed a model for detecting communities in web with the help of Particle Swarm Optimization (PSO). Authors showed that the performance of algorithm can be better if the inertia weight and swarm size is appropriately selected.

Clara Pizzuti [13] presented a genetic algorithm for uncovering communities in large networks named GA-Net. They introduced the concept named community score. The underlying objective of the algorithm is to maximize the value of community score for obtaining optimal partitioning of the network. The author also introduced the Safe individual criteria in genetic algorithm to avoid the useless computation thus by making the algorithm efficient.

Clara Pizzuti [14] further modified his work by presenting a new genetic algorithm to discover optimal communities in complex networks named MOGA-Net i.e. multiobjective genetic algorithm basically a Nondominated Sorting Genetic Algorithm (NSGA-II) that builds and ranks the competing individuals population on nondominance basis. The approach uses hierarchal clustering technique producing network communities at different level of hierarchies and automatically resolute communities formed.

Gong et al. [15] proposed a Nondominated Neighbor multiobjective immune algorithm based on Local Search for Dynamic Network and named it as DYN-LSNNIA. The algorithm uses modularity as optimization function, is tested on four synthetic and two real world networks and observed that algorithm not only detect accurate community structure but also more stable than the state of the art algorithms.

Amiri et al. [16] proposed a new multi-objective optimization algorithm based on enhanced firefly algorithm (EFA) using Fuzzy- based grouping and mutation techniques for the detection of network communities. The proposed approach was strengthened with a smart population method. The algorithm also detected network communities where the number of communities was not initially known. The results were compared with other algorithms like MOGA-Net, Bondel, RN, CNM, Infomod and original firefly algorithms.

Ma et al. [17] proposed fast multi-level memetic algorithm for community detection named MLCD that uses genetic algorithm (GA) with multi-level learning strategies. The proposed hybrid global-local search algorithm used Label propagation method for updation of community identifier of each vertex at each procedure. The results showed a lesser computation time in comparison with original memetic algorithm.

Honghao et al. [18] proposed an Ant Colony Optimization (ACO) method for detecting communities in networks using max-min ant system method for community detection. The two important points of their method are one solution is in the form of locus-based adjacency in which communities are taken as linked components of networks and second the structural information was included in the algorithm and thus a new heuristic was proposed, based on association between nodes.

Shang et al. [19] proposed a community detection method based on modularity and an improved genetic algorithm named as MIGA. The authors also used prior information regarding the number of detecting communities. MIGA used simulated annealing algorithm for local searching.

Hafez et al. [20] used Artificial bee colony (ABC) optimization technique to solve the community detection problem. The objective functions used in this algorithm were divided into two categories. The first category of objectives consisted of Conductance, Internal Density, Normalized Cut, Cut Ratio, Expansion, Average-ODF, Flake-ODF and Maximum-ODF. The second category of objectives consisted of Modularity, Community Fitness and Community Score. The solution of the community detection problem was obtained by minimizing the first category and maximizing the second category. The method used is locus-based adjacency for representation of communities in ABC algorithm

B.Orgaz, Gema, and D. Camacho [21] applied graph clustering algorithms based on a genetic algorithm. They designed a new fitness function to guide the clustering process based on different measures of network topology (Density, Heterogeneity, Centralization, Clustering Coefficient, Neighbourhood). The proposed approach was experimentally tested using a real-world social network (Eurovision dataset).). The authors did a comparative assessment of network measures to choose the better measures for the fitness function. The experimental results obtained are compared to other clustering algorithms (CPM methods and GCF algorithm). The results depicted better results using new approach than the other approaches studied.

The authors Gong, Maoguo, et al. [22] proposed a new community detection algorithm, MOEA/D-Net, to simultaneously optimize two contradictory objective functions, Negative Ratio Association and Ratio Cut. Optimization of Negative Ratio Association inclined to divide a network into small communities, while the optimization of Ratio Cut used to divide a network into large communities the proposed algorithm maximizes the density of internal degrees, and minimizes the density of external degrees simultaneously. It can produce a set of solutions which can represent various divisions to the networks at different hierarchical levels. The number of communities is automatically determined by the nondominated individuals resulting from our algorithm. Experiments on both synthetic and real-world network datasets verify that our algorithm is highly efficient at discovering quality community structure

• III.    Comparative Analysis of Various Approaches

Two functions have been used for the comparison of various approaches one being modularity and the other as normalized mutual information.

• A.    Four real world networks

The four real world networks which are mostly used as a benchmark networks for community detection in networks are Zachary’s Karate Club, Bottlenose Dolphins, Books about US politics and American college football network [18].

Zachary’s karate club as stated is mostly used as a community detection networks. This club consists of 34

members that are represented as 34 nodes and the relationships between the club members is represented as edges [20].

Dolphins network is proposed by Lusseau after observing the behavior of dolphins [20]. The 62 dolphins in this network are represented as nodes and the connections between these dolphins are represented as edges.

Girvan and Newman proposed a network that represented different football teams as nodes and the matches between any two teams as edges which was named as American college football club [3].

The book about US politics is a network published in 2004. Newman divided this network in three communities on the basis of reviews and descriptions [4].

• B.    Modularity

The Modularity evaluates the quality of cluster which signify the extent to which a given community partition is distinguished by high number of intra-community connectivity in comparison to inter-community ones [3].

The Modularity (Q) [3, 4, 18] value can be mathematically stated as in (1).

Q ^{= ∑1}, i^AU ^- s»^{(1 ,} i ) (1)

Where, A , is the adjacency matrix, m is the number of edges in network, d1,dj are the degree (or strength) of nodes i,j and δ(i, j) is the function which return 1 when both i, j are in same community, 0 otherwise. Table 1 and Table 2 shows the summarisation of both analytical and evolutionary approaches involved in solving the problem of community detection

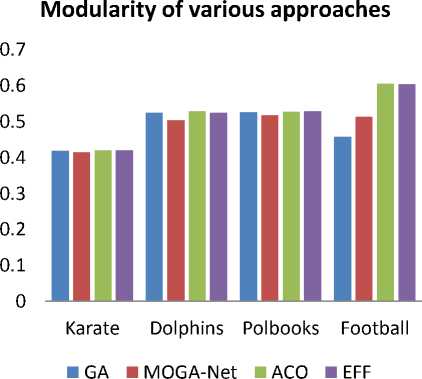
Fig.1. Comparison of Various Approaches on the Basis of Modularity Values for four Real World Networks

Fig.1 represents the graph obtained by plotting the modularity values obtained in GA [13], MOGA-Net [14], ACO [18] and EFF [16] when tested on four real world networks i.e. Zachary karate, Bottle nose dolphins, Books about US politics and American football club.

As shown in Fig. 2, ACO and EFF has high modularity value for karate network, ACO has highest modularity value for dolphins, EFF has highest modularity for polbooks and ACO has highest modularity value for football.

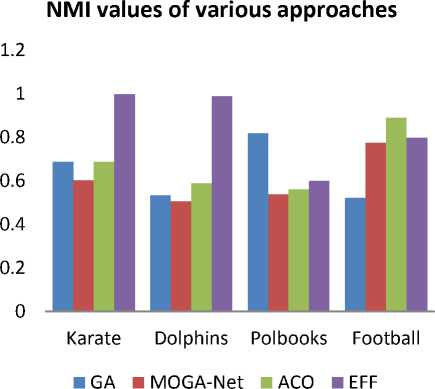
Fig.2. Comparison of Various Approaches on the Basis of NMI Values for four Real World Networks

• C.    Normalized Mutual Information (NMI)

Normalized mutual information (NMI) is the performance measure [6] that quantifies the similarity between the detected and true community structure.

NMI denoted as I (X, Y) [4] is calculated using the following formula as shown in (2).

I (X, Y) =

___2^∑1^∑ ^cij i°9 ( ^C< ^․ 2 )

^∑ i2i^ci ^․ log ( Ci / N )+ ∑    ^C . jiog ( c . i / N )

Where X and Y denotes two network structures, C - the confusion matrix . Cij - the number of nodes present in community i of X as well as in community j of Y , CX (CY) - the number of classes in part X and Y, Ci.C . -the number of elements in row i (column j) of C, N -the total number of nodes in networks.

The greater the value of NMI, the more similar the true and detected communities are i.e. better the solution quality [3]. For both communities being same, the NMI value equals 1 and NMI=0 signifies different communities.

Table 1. Shows the Summarization of Various Analytical Approaches