Вейвлет-преобразования в задачах контроля и диагностики автоколебаний стана холодной прокатки

Автоколебания стана холодной прокатки – реально существующее явление, для борьбы с которым разрабатываются и внедряются различные контрольные и диагностические системы. При возникновении автоколебаний амплитуда возрастает скачком более чем в сто раз: от 2–3 м/с2 до 200–250 м/с2. Частоты колебаний составляют от 100 до 500 Гц, т. е. число циклов нагружения даже за несколько секунд может достигать нескольких тысяч. Причинами могут быть крутильные колебания [1, 2], параметрические возбуждения [3, 4], фрикционные автоколебания [5, 6] – при прокатке трение между полосой и рабочими валками на больших скоростях могут появляться неконсервативные силы, приводящие к возникновению автоколебаний. По характеру колебаний они (автоколебания) могут быть различными, например, с очень низкими амплитудами, приводящими к дефектам поверхности [7], но не приводящими к разрывам полосы и не угрожающими разрушением стана. Могут быть и с очень высоким уровнем амплитуд колебаний и в этом случае приводящие к непосредственным разрушениям, так и, при длительном воздействии, к появлению трещин элементов и узлов стана. Причина малоцикловая или многоцикловая усталость. Как правило, автоколебания на станах холодной прокатки возникают на тонких полосах, с тол- щиной менее 1 мм [8] и высоких скоростях прокатки [9]. Основным мероприятием по устранению автоколебаний является раннее предупреждение и снижение скорости прокатки при возникновении автоколебаний. Для контроля станы оснащаются виброаппаратурой с аналоговым либо цифровым контролем [10, 11]. Соответствующее программное обеспечение позволяет контролировать спектральный состав и выделять опасные составляющие. Аналоговые системы предупреждают о повышении уровня вибрации, превышении допустимых норм и выдают команду о снижении скорости прокатки. Цифровые системы, позволяющие контролировать не только амплитуду, но и спектральный состав, даже при низких уровнях вибрации могут диагностировать и предупреждать возникновение дефектов, связанных с неравнотолщинностью полосы. Стандартно используемое при анализе и диагностике технического состояния быстрое преобразование Фурье [12] определяет структуру спектрального состава в случае стационарного процесса и плохо справляется в случае нестационарного процесса. Не позволяет определить время возникновения автоколебаний. С целью определения момента возникновения автоколебаний могут использоваться новые методы контроля, например преобразование Фурье на коротком временном интервале (Short-time Fourier transform) [13, 14]. В этом случае интервал дискретизации разбивается на несколько равных промежутков времени, в каждом из которых производится быстрое преобразование Фурье. Еще одним эффективным способом контроля является вейвлет-преобразование [15, 16]. Впервые в металлургии в прокатном производстве использование методов вейвлет-преобразований предложено в работах Маслова Е.А., Харахнина К.А. [17]. Использование вейв-лет-преобразования представлено в работах [18–20].

С развитием информационных технологий появились новые возможности и, как следствие, новые термины. К таким в первую очередь можно отнести «цифровой двойник», «цифровая тень». Цифровая тень, цифровой след или электронный след – это данные, которые остаются при использовании Интернета [21]. Пассивный цифровой след пользователь оставляет ненамеренно, он получается автоматически из данных, которые получают и сохраняют автоматически. Активный цифровой след – это информация, которой пользователь делится по собственному желанию.

Одно из определений «цифровой тени» дано в работе [22]: «Цифровая тень» – отдельные факты о действиях анализируемого субъекта, отраженные и сохраненные внешней по отношению к нему информационной средой».

При проведении промышленного эксперимента, как правило, используются данные, технологические параметры или диагностические данные, отраженные и сохраненные во внешней по отношению к промышленному объекту среде, т. е. используется «цифровая тень». Фирмой «СИГМА» разработана и внедрена система контроля, сбора и длительного хранения технологических параметров стана холодной прокатки 2000. Система хранения представляет собой гибридную базу данных, включающую в себя, кроме технологических параметров, данные виброконтроля. Вибропараметры собираются и хранятся в отдельной базе данных. Частота опроса 8000 измерений в секунду (0,125 миллисекунд на одно измерение). Технологические параметры собираются с частотой опроса 100 или 200 измерений в секунду. Базы данных технологических и вибрационных параметров объединены графической оболочкой. По вибрационным параметрам определяется момент возникновения автоколебаний стана. Технологические параметры позволяют связать возникновение автоколебаний с процессом прокатки на стане.

Промышленный эксперимент

При ручном контроле набора скорости прокатки появление автоколебаний происходит при наборе скорости прокатки. В ручном режиме формируется сигнал АСУ ТП на снижение скорости прокатки. При высоких уровнях вибрации стан останавливается полностью. Затем, после непродолжительного останова, запускается снова. Если уровень вибрации ниже определенного предела, скорость прокатки снижается, например, с 22 до 10 м/с, затем, после стабилизации вибрационного состояния, продолжается набор скорости прокатки. На рис. 1 приведены два случая автоколебаний с различным уровнем пиковых значений виброускорения. В 8 часов 50 минут амплитуда виброускорений составляет 225 м/с ² с полным остановом стана, в 9 часов 30 минут – 130 м/с ² с частичным снижением скорости прокатки до 10 м/с.

Исследование автоколебаний с уровнем вибраций 225 м/с ²

Уровни высокие, примерно в 100 раз выше по сравнению с уровнем вибрации при нормальной прокатке полосы. Вибрация скачком увеличивается от 2–3 м/с2 до 150–250 м/с2 . И хотя время про- должения режима автоколебаний всего 2 секунды, этого достаточно, чтобы получить порядка тысячи циклов нагружения. Десять случаев автоколебаний – это уже 10 000 циклов нагружения. При высоких уровнях вибрации и, как следствие, высоких уровнях напряжений 10 000 циклов достаточно для возникновения трещин, например, плит CVC. Хотя это только пример, есть ли связь между появлением трещин на плитах CVC и автоколебаниями клети стана – неизвестно.

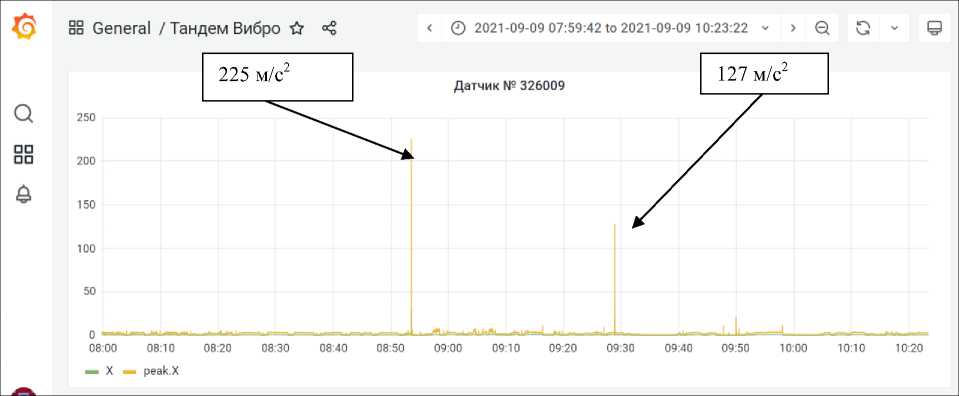
Рис. 1. Автоколебания клети стана холодной прокатки 2000

Fig. 1. Self-oscillation of the rolling cage of the cold rolling mill 2000

На рис. 2 представлены пиковые значения виброускорений в трех взаимно перпендикулярных направлениях в режиме автоколебаний. Максимальные значения продольной составляющей – 225 м/с ² , совпадающей по направлению с прокаткой в поперечном направлении – 163 м/с ² и в вертикальном направлении – 57 м/с ² .

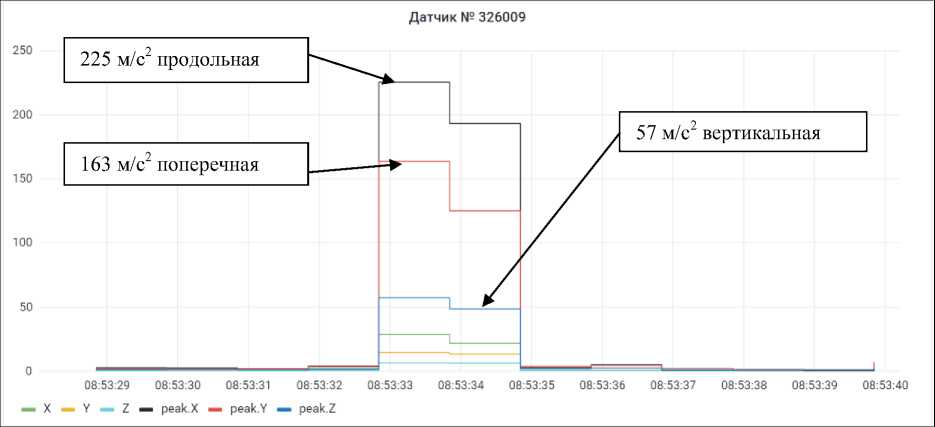
Рис. 2. Пиковые значения виброускорения 4 клети в момент возникновения автоколебаний (м/с2) Fig. 2. Peak values of vibration acceleration of the rolling cage 4 at the time of occurrence of self-oscillations (m/s2)

Измерение вибрации производилось с частотой опроса 8000 измерений в секунду, при этом частота Найквиста, в соответствии с теоремой Котельникова, составляет 4000 Гц. В качестве результата измерений получаем реализацию виброускорений на каждую отдельную секунду все 8000 точек измерения (рис. 3) и спектральную характеристику (рис. 4).

Как видно из реализаций (см. рис. 3), автоколебания развиваются не сразу. Вначале всплеск вибрации с малой амплитудой, затем в течение 0,3 с вибрация равна нулю и, наконец, развитое состояние автоколебаний. По внешнему виду колебания релаксационные, разрывные, характер- ные для фрикционных автоколебаний. Частотный состав очень широкий (рис. 5), первая гармоника – 120 Гц, вторая, третья, четвертая – до 600 Гц.

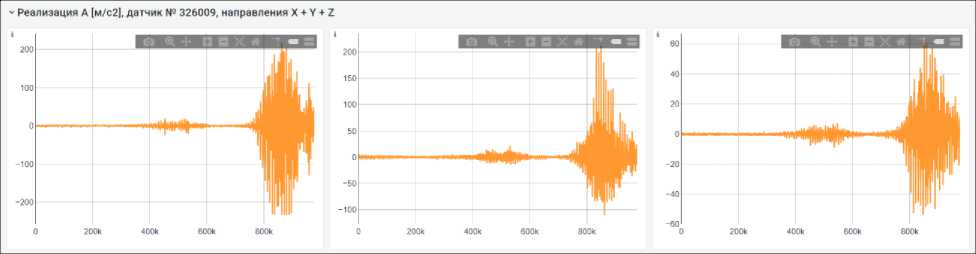
а                                     b                                     с

Рис. 3. Реализации виброускорений в продольном (а), поперечном (b) и вертикальном (с) направлениях, первая секунда

Fig. 3. Realization of vibration accelerations in the longitudinal (a), transverse (b) and vertical (с) directions

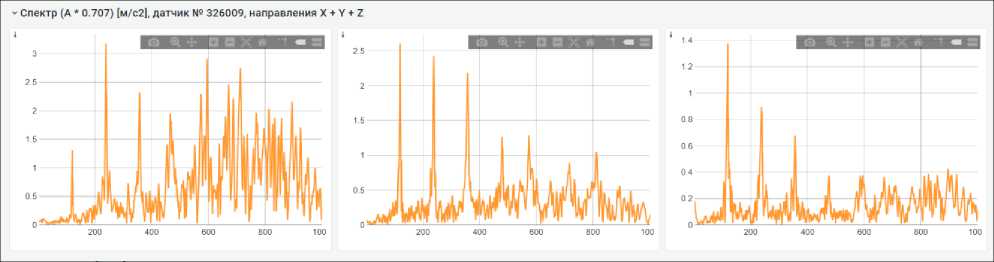
а                                        b                                        с

Рис. 4. Спектральный состав виброускорений в продольном (а), поперечном (b) и вертикальном (с) направлениях Fig. 4. Spectral composition of vibration accelerations in the longitudinal (a), transverse (b) and vertical (c) directions

Возникновение автоколебаний происходит на скоростях проката в районе 21–22 м/с. При максимальном уровне вибрации на скорости 21,5 м/с происходит отключение стана (см. рис. 5). При скорости прокатки 17,5 м/с вибрационное состояние нормализуется, уровень виброускорений становится равным 3 м/с ² . Полный останов стана происходит в течение 5 секунд с ускорением 4,5 м/с ² .

Важно, что переход из состояния автоколебаний в нормальное вибрационное состояние происходит за 1 с, т. е. если мы сможем определить момент зарождения автоколебаний хотя бы на секунду раньше, сможем работать без автоколебаний.

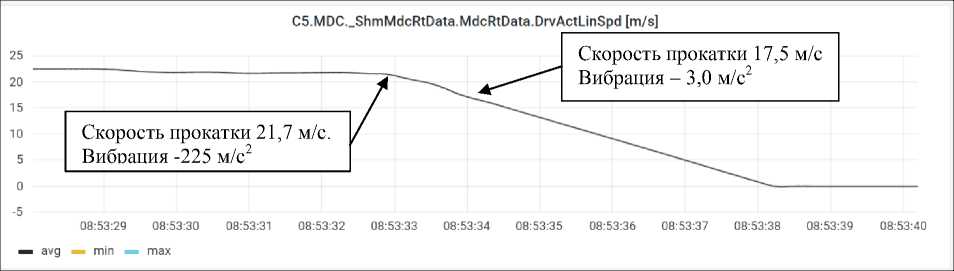
Рис. 5. Скорость прокатки 5 клети в момент возникновения автоколебаний (м/с)

Fig. 5. Rolling speed of the 5 rolling cage at the moment of occurrence of self-oscillations (m/s)

На рис. 6 приведены автоколебания гидравлического натяжного устройства (ГНУ). Максимальный уровень виброперемещений 100–120 мкм. Колебания гидравлического натяжного устройства происходят в вертикальном направлении синхронно с колебаниями клети стана и про- должаются в течение 2 с. Отключение стана происходит вручную в момент максимальных виброперемещений ГНУ.

0.950

0.900

0.850

0.800

0.750

0.700

08:53:29    08:53:30    08:53:31    08:53:32    08:53:33    08:53:34    08:53:35    08:53:36    08:53:37    08:53:38    08:53:39    08:53:40

■ avg ■ min ■ max

Рис. 6. Виброперемещения гидравлического натяжного устройства (ГНУ) клети стана

Fig. 6. Vibration displacement of the hydraulic tensioner (GNU) of the mill stand

Примерно за полторы секунды до начала автоколебаний клети стана и ГНУ начинают формироваться автоколебания прокатываемой полосы, фиксируются по натяжению полосы (рис. 7). Зарождение автоколебаний, происходит на скорости прокатки 22 м/с в течение 2–3 с. Максимальные уровни колебаний натяжения 140–150 кН. Колебания натяжения прокатываемой полосы не совпадают по фазе с виброперемещениями ГНУ. Частота опроса при измерениях перемещений ГНУ – 5 мс, натяжения полосы – 10 мс. Режим автоколебаний в увеличенном масштабе приведен на рис. 8.

Скорость прокатки 22 м/с                          Скорость прокатки 17,5 м/с

Начало развития автоколебаний                    Амплитуда колебаний натяжения 10 КН

Момент останова стана

Скорость прокатки 22 м/с

Момент останова стана

08:53:29    08:53:30    08:53:31    08:53:32    08:53:33    08:53:34    08:53:35    08:53:36    08:53:37    08:53:38    08:53:39    08:53:40

— avg — min — max

Рис. 7. Натяжение прокатываемой полосы в режиме автоколебаний Fig. 7. Tension of the rolled strip in the self-oscillation mode

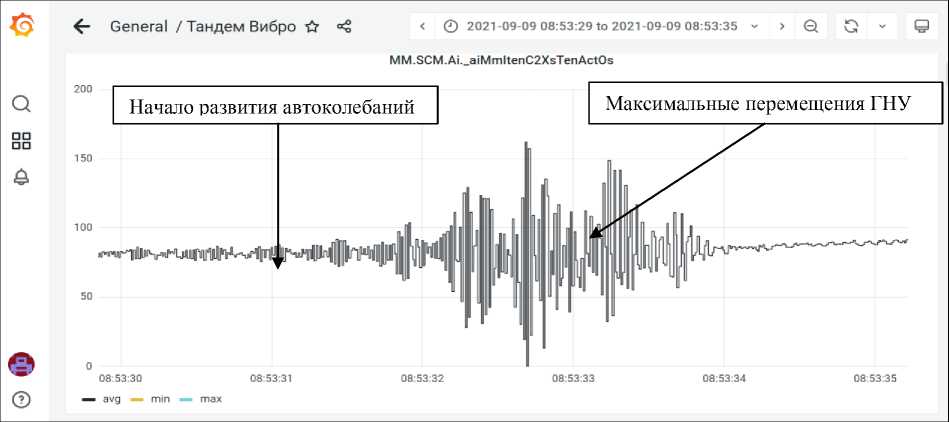
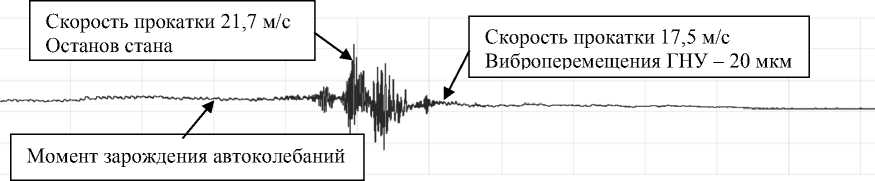
Рис. 8. Натяжение прокатываемой полосы в режиме автоколебаний в увеличенном масштабе Fig. 8. Tension of the rolled strip in the self-oscillation mode on an enlarged scale

Исследование автоколебаний с уровнем вибраций 127 м/с 2

На рис. 9 представлены пиковые значения виброускорений в трех взаимно перпендикулярных направлениях в режиме автоколебаний при снижении скорости прокатки с 22 до 10 м/с.

На скорости 10 м/с уровень вибрации становится нормальным, в пределах требований стандарта. Максимальные значения продольной составляющей – 127 м/с ² , совпадающей по направлению с прокаткой в поперечном направлении – 83 м/с ² и в вертикальном направлении – 26 м/с ² .

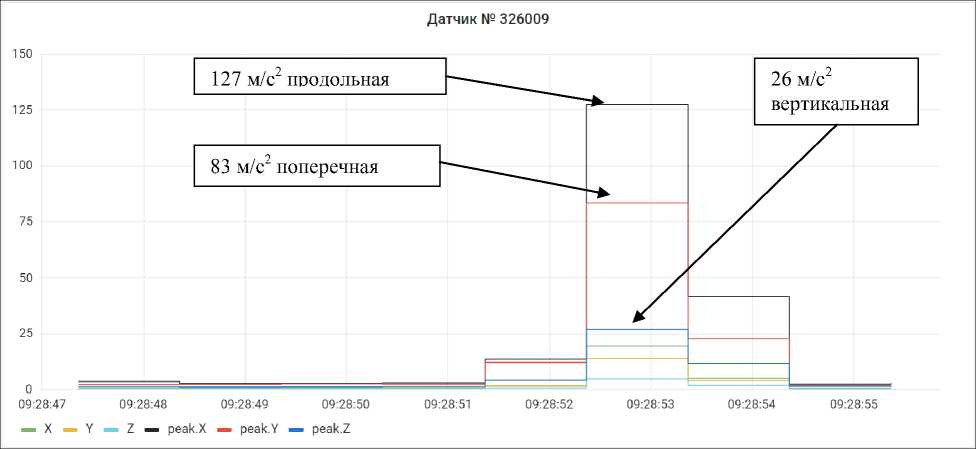
Рис. 9. Пиковые значения виброускорения 4 клети в момент возникновения автоколебаний (м/с2)

Fig. 9. Peak values of vibration acceleration of the 4 rolling cage at the time of occurrence of self-oscillations (m/s2)

Возникновение автоколебаний происходит на скоростях проката в районе 21–22 м/с. При максимальном уровне вибрации на скорости 21,5 м/с происходит резкое снижение скорости стана до 10 м/с с ускорением примерно 3,0–3,5 м/с ² (рис. 10). При скорости прокатки 17,5 м/с вибрационное состояние нормализуется, уровень виброускорений становится равным 3 м/с ² . Полный останов стана происходит в течение 5 секунд с ускорением 4,5 м/с ² .

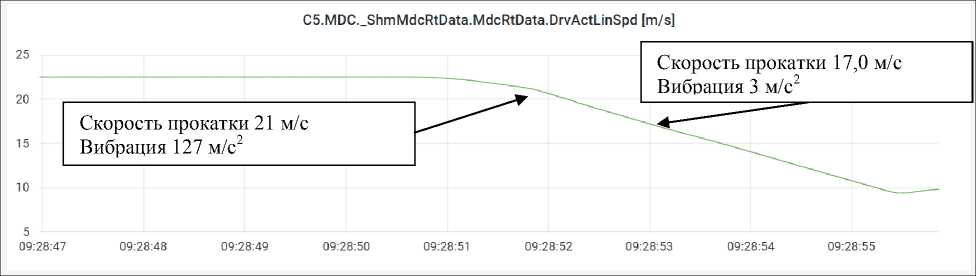
Рис. 10. Скорость прокатки 5 клети в момент возникновения автоколебаний (м/с)

Fig. 10. Rolling speed of the 5 rolling cage at the moment of occurrence of self-oscillations (m/s)

На рис. 11 приведены автоколебания гидравлического натяжного устройства (ГНУ). Максимальный уровень виброперемещений 100–120 мкм. Колебания гидравлического натяжного устройства происходят синхронно с колебаниями клети стана и также продолжаются в течение 2 с. Отключение стана происходит вручную в момент максимальных виброперемещений ГНУ.

Примерно за полторы секунды до начала автоколебаний клети стана и ГНУ начинают формироваться автоколебания прокатываемой полосы, фиксируются по натяжению полосы (рис. 12). Зарождение автоколебаний происходит на скорости прокатки 22 м/с в течение 2–3 с. Максимальные уровни колебаний натяжения 140–150 кН. Колебания натяжения прокатываемой полосы не совпадают по фазе с виброперемещениями ГНУ.

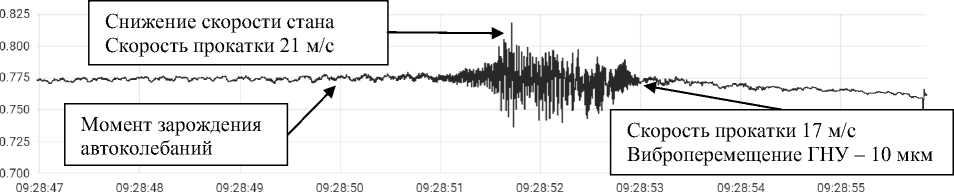
■ avg — min — max

Рис. 11. Виброперемещения гидравлического натяжного устройства (ГНУ) клети стана

Fig. 11. Vibration displacement of the hydraulic tensioner (GNU) of the mill stand

На рис. 13 показано натяжение прокатываемой полосы в режиме автоколебаний в увеличенном масштабе. В момент зарождения автоколебаний уровень вибрации составляет примерно 15– 20 кН, что достаточно для численного определения момента возникновения автоколебаний и выработки сигнала АСУ ТП.

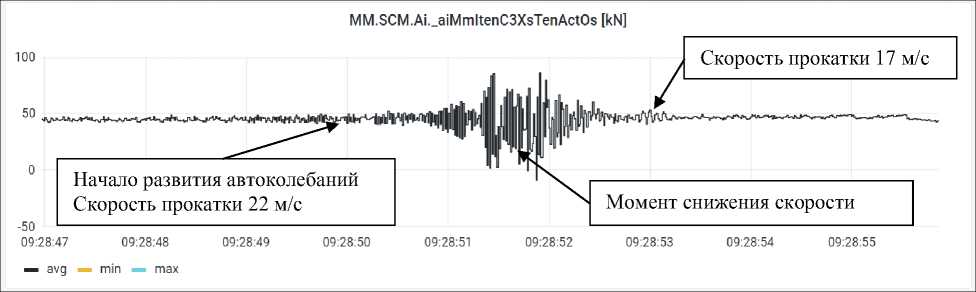
Рис. 12. Натяжение прокатываемой полосы в режиме автоколебаний Fig. 12. Tension of the rolled strip in the self-oscillation mode

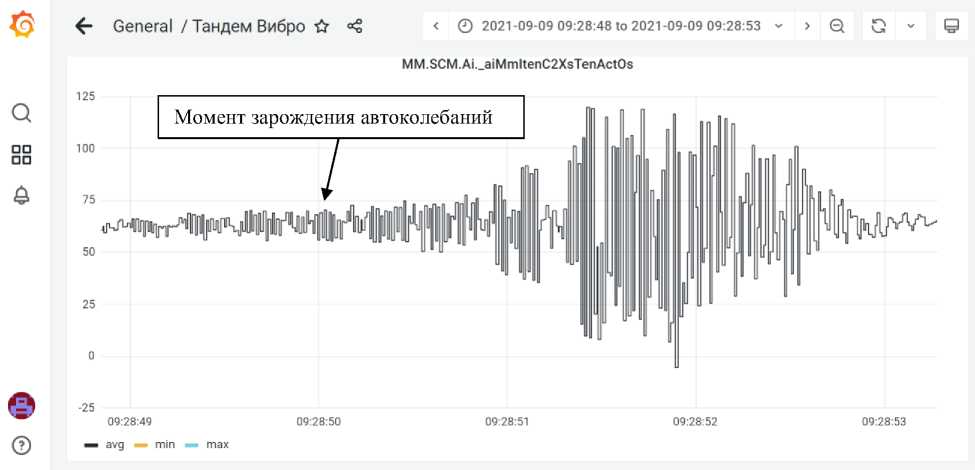
Рис. 13. Натяжение прокатываемой полосы в режиме автоколебаний в увеличенном масштабе Fig. 13. Tension of the rolled strip in the mode of self-oscillations on an enlarged scale

Численные методы контроля момента возникновения автоколебаний

Природа возникновения автоколебаний клетей стана – это фрикционные колебания прокатываемой полосы. Причем автоколебания полосы зарождаются за 2–3 с до развитых автоколебаний клетей. Как показывает промышленный эксперимент, при снижении скорости прокатки с ускорением 4–5 м/с ² достаточно одной секунды для стабилизации вибрационного состояния. За две 2 с необходимо определить момент зарождения, выработать сигнал АСУ ТП и снизить скорость прокатки до 17,5 м/с.

Собственная частота автоколебаний первой гармоники, полученная экспериментально, равна 115 Гц. Момент появления частоты 115 Гц можно определить, используя быстрое преобразование Фурье, быстрое преобразование Фурье за короткий момент времени или вейвлет-преобразование. Тригонометрический ряд Фурье, который используется при вычислении БПФ, можно записать в виде [23]:

f ( X )=у^{+∑ ∞} ₌ ^(й_п cos TLX + bn sin nx )․                                             (1)

Для стационарных систем ряд Фурье функции f ( X ) сходится точно. Для нестационарных систем автоколебания клетей не стационарные, разрывные, релаксационные, ряд Фурье функции f ( X ), вообще говоря, не обязан сходиться к ней точно. Кроме того, для определения спектральной характеристики с точностью от 1 до 2 Гц необходимо не менее 0,5–1,0 с. Сократить время обработки сигнала с достаточной степенью точности можно используя, например, преобразование Фурье на коротком временном интервале (Short-time Fourier transform) [13, 14].

Существует еще один метод определения момента возникновения автоколебаний прокатываемой полосы. Это вейвлет-преобразование [18, 24], которое достаточно часто используют в системах вибродигностики. Простейшим примером ортогонального вейвлета является HAAR вейвлет, определяемый соотношением:

1,0≤ t _<1

V" ⁽ t ⁾⁼ -1,¹  ≤ t <²1                                                        (2)

• 0, t <0, t ≥1․

Наиболее часто используется вейвлет Морле:

V ( t )= exp ( i (Oq t ) exp ^ -Э ․                                                        (3)

Вейвлет Морле эффективен на гладких тригонометрических функциях, но существенно медленнее вейвлета Хаара [25, 26].

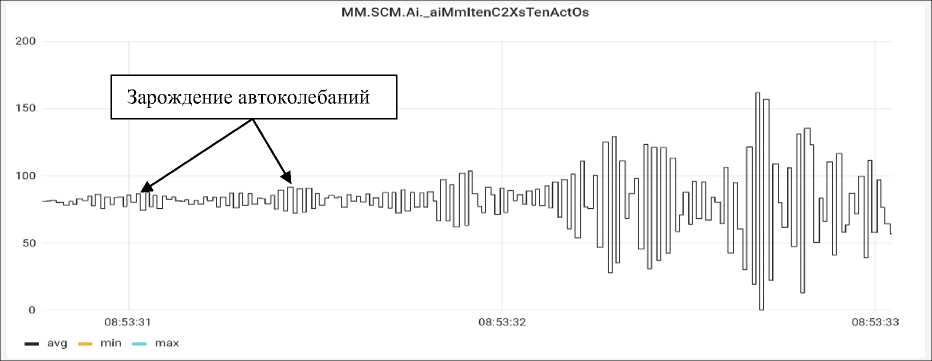
Рис. 14. Натяжение. Не гладкая функция Fig. 14. Tension. Not a smooth function

Выводы

• 1.    Автоколебания клетей стана являются следствием фрикционных автоколебаний прокатываемой полосы. Между автоколебаниями полосы и автоколебаниями клетей стана запаздывание примерно 2–3 с.

• 2.    Используя современные методы анализа спектрального состава вибрационного сигнала возможно оперативно и надежно определять момент зарождения автоколебаний.