Векторные аддитивные схемы для некоторых классов уравнений гиперболического типа

Для численного решения многомерных задач математической физики используются различные классы аддитивных схем (схем расщепления [1–2]). В работах [3–4] для решения многомерных задач предложен новый класс безусловно устойчивых схем переменных направлений полной аппроксимации. Устойчивость и сходимость таких схем исследуется на основе получения соответствующих априорных оценок. В работе [5] основные принципы построения векторных аддитивных схем на основе операторно-разностных подходов применены к абстрактной задаче Коши. В работе [6] на основе общей теории устойчивости разностных схем [1, 7] проводится исследование векторно-аддитивных схем с самосопряженными операторами. В работе [8] на основе общей теории устойчивости операторно-разностных схем А. А. Самарского проводится исследование векторных аддитивных схем для общих эволюционных уравнений первого порядка с несамосопряженными операторами. В [9] на основе принципа регуляризации построены новые аддитивные операторно-разностные схемы полной аппроксимации. В [10] исследуется устойчивость в произвольных нормах векторной аддитивной схемы. Показано, что устойчивость имеет место при условии, что устойчивыми являются чисто неявные схемы для отдельных компонент.

В [11] построены регуляризованные аддитивные операторно-разностные схемы для эволюционных задач без предположения о перестановочности регуляризующего оператора и оператора задачи, отмечены возможности обобщения предложенных регуляризованных аддитивных схем на задачи с несамосопряженными операторами и уравнения второго порядка.

В данной работе проводится исследование векторных аддитивных схем для псевдопа-раболических уравнений (уравнение влагопереноса Аллера [12, с. 137]), волнового уравнения в релаксирующих средах (см. [13, с. 84]) и волнового уравнения с учетом вязкости и теплопроводности (см. [13, с. 22]).

Существование и единственность решений, рассматриваемых здесь краевых задач, были исследованы в работах одного из авторов [14, 15].

В уравнениях, рассматриваемых в этой работе, содержатся смешанные производные u x _a x _a t , u x _a x _{a tt} , a = 1,p. В этом случае не удается построить разностные схемы на основе понятия суммарной аппроксимации. Например, доказательство сходимости локальноодномерной схемы проводится (см. [1, с. 528]) с помощью введения П (_а) в задачу для погрешности z (_а) = V ( _a ) + П ( _а ) - В нашем случае в правую часть уравнения для v ( _а ) = v j+ p , ^ а вмешиваются слагаемые Л а n _at = O(1), Л а у = У х а Х а , ^т- е ^ а = Л а П (а) + Л а П _а 1 + ^ а , где Л _а П ( _а ) = О(т ), < = O(h а + т ). При p = 2 можно получить априорную оценку не вводя П ( _а ) (см. [7, с. 336]), но только для уравнений, не содержащих смешанные производные. Аддитивные схемы полной аппроксимации [3–10] оказываются более приемлемыми для численного решения рассматриваемых здесь задач.

1.    Волновое уравнение в неидеальной среде с учетом вязкости и теплопроводности

В цилиндре Qt = G х (0, T], основанием которого является p-мерный параллелепипед G = {x = (xi,X2,..., xp) : 0 < xа < 1а, a = 1,p}, рассмотрим задачу d2uvp-'

dt^ + Lu = f (x,t), Lu = ^2Lаu, (x,t) € Qt,(1.1)

а=1

u|sT = 0, u(x, 0) = uo(x), ut(x, 0) = u1(x),(1.2)

где Ь а u = - [ дд а ( к а (x) du ) + ддд а (Mx) dU )] , G = G +Г. S t = Г х [0,T] — боковая поверхность цилиндра Q t , 0 < c i 6 к _а (x) 6 C 2 , a = 1,p, к _а (x), f (x,t) таковы, что решение задачи (1.1)–(1.2) существует, единственно и обладает требуемой гладкостью.

Уравнение вида (1.1) возникает в теории волн (см. [12, с. 85]). Оно учитывает потери энергии, связанные с вязкостью и теплопроводностью. Третий член в левой части уравнения (1.1) описывает затухание звука из-за вязкости и теплопроводности, обычно перед ним стоит диссипативный коэффициент. Ради простоты мы положим его равным единице.

Задачу (1.1)–(1.2) перепишем в виде абстрактной задачи Коши d2u + Au + Adu = f (t), A = XX Аа, Аа = - ^-каа (x)            (1.3)

dt ²            dt               ^z—‘              дx _а V       дx_а )

=

u(0) = u o , u t (0) = u i ,

(1.4)

с линейным самосопряженным положительно-определенным оператором А : H ^ H , действующим в некотором гильбертовом пространстве H со скалярным произведением (u, v) = Jg uv dx, А _а — положительно-определенные операторы в H.

Краевые условия учитываются включением u(t) € D(A), где D(A) — область определения оператора А. Вместо одного скалярного решения u(t) вводится вектор решений

U(t) = (u i (t), u 2 (t),..., u p (t)) (см. [3-10]). Вместо исходной задачи (1.3)-(1.4) запишем систему однотипных подзадач:

d ² u _a dt ²

pp

⁺ X A e u e ⁺ X A e u et = f ^{( t )} , e=i        e=i

(1.5)

U a (0) = u o , U at (0) = U i ,  a = 1,p.

(1.6)

2.    Устойчивость по правой части и начальным данным решения вспомогательной системы

Заметим, что дифференциальные операторы A _a , a = 1,p, порожденные дифференциальными выражениями L a u = — d^- ( k _a (x) д^т") и условиями

u(xi,..., xa-i, 0, xa+i,..., xp, t) = u(xi,..., xa-i, la,xa+i,..., xp, t) = 0, t E [0, T], ka (x) > ci > 0, a = 1,p, являются постоянными (не зависят от t), самосопряженными и положительно определенными.

Утверждение. Задача (1.5) - (1.6) , полученная в результате перехода от скалярного решения задачи (1.3) - (1.4) к вектор-решению, поставлена корректно, причем u _a (t) = u(t), a = 1,p, для t E [0, T] и справедлива оценка

p kuαxαt

p k2 + Va.

2 ^p

6 M k f «Эд. + k AU o k ² + £ « U i. . k ² , =i

(2.1)

t kf k2,Qt = I kf k2 dT, kf k2 = I f2(x) dx. 0

<1 Пусть za = ua — u. Подставляя ua = za + u в уравнение (1.5), находим d2z^    p           p                    ___

^t2a +12 Aeze+ 52 Aezet = 0, a = 1,p, e=i

(2.2)

Za (0) = Zat (0) = 0.(2.3)

Каждое из уравнений (2.2) умножим скалярно на A _a ^d Z a и просуммируем их по a = 1,p. Тогда получим

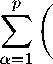
д ² Z a dt ²

. dza\   1 д

Aa^f +о^7 dt /   2 dt

p

A α z α

(2.4)

С помощ ью интегрирования по частям, с учетом граничных условий и вида оператора A _a , a = 1,p, из (2.4) находим

^{1 д} X (k _г2   \ ,1 £

2 dt    v^{a ,Z ax} “ t) ⁺ 2 dt

p

A α z α

p

+ EAa t

= 0.

(2.5)

Проинтегрируем (2.5) по т от 0 до t с учетом условий (2.3). Тогда получим

p

1Х(ь z2 .

2 / у v^o^t

p

) +1 EA > Z a

⁺ AX Aa^

0   ^a =

dT = 0.

Откуда с помощью (2.2) получаем

"

dt ^{2      0 ,}

Z a (0) = Z at (0) = 0, a = 1,p.

(2.6)

Из (2.6) находим, что z _a (t) = 0 или U _a (t) = u(t), a = 1,p.

Для получения априорной оценки (2.1) умнож им уравнение (1.5) скалярно на A _α ^∂ _∂ ^u _t ^α и просуммируем полученное равенство по a, a = 1,p:

/ d ² U a . dU a M dt ² ’ ^{A a} dt

p

1 d v-^ л

⁺ 2 dt 2^A ^{a u}

α

p

+ XA a U at

2 P V я \

XA

I ^f,2^^{A a} dt .

\ a=i        /

(2.7)

Так как

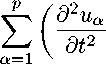
∂u α , A α _∂t

2 at X ( k ^a '“ ^ax.^t

f' ^X Aa X 6 2 1 1 f 11 2 +2

, ^du a

A α _∂t

то из (2.7) имеем

p ci X Huaxct a=i

k ² + XA a U a

откуда следует неравенство (2.1). B

2 ^p

^{6 k f k} 2,Q _t ⁺ k Au o k ² + c 2 X llu lx a II² ' a=1

3. Устойчивость разностной схемы

Для приближенного решения задачи (1.5)–(1.6) будем использовать трехслойную векторную аддитивную схему

αpαp yatt + X Aheye + X AheУв + X Aheyet + X Aheyet = f'

e=i         e=a+i         e=i

ya(0) = Uo, yat(0) = Ui, a = 1, 2,... ,p,(3.2)

где

(a+i+i)yio+l-yia _ a(ia)yia - yia-i A hayia = (aayXa )ХоХа = 7 I aa          r          aar hα            hα               hα

^{a ( i a )} = k a ⁽ x i ^,...^,x a ^{a - i / 2} ' . . . '^x p ⁾ '    y t = ^{( y -} y ^{) /T},   y att = ^{( y} i a ^- 2y i a ⁺ y i a ^{) /т 2} ,    ^a = 1,P,

— разностные операторы, аппроксимирующие на сетке

^ hT = Ш h X Ш т

p

^Ш h = П^Ш h a , a=i

^■^ h — ^x a    — ia h a * ^a — ^{1 ,p} ; i a — ⁰, ¹ '...' N a , h a — l a / N a ^ ,

Шт = {tj = jT * j = 0, 1,... ,jo} дифференциальные операторы AaU = - d|a (ka (x)dxu;) , ^jtu, у = yj+i, у = yj, у = yj i

Введем, как обычно, скалярные произведения и нормы

N 1 - 1 N - 1   N a - 1   N p - 1

p

H = Y h a , k y k ² = (y,y), a =1

N 1 - 1 N 2 - 1     N a     N p - 1

i 1 =1 i 2 =1     i _a =1     i p =1

Из контекста будет ясно о какой норме идет речь, поэтому, чтобы не загромождать изложение, индекс а при написании нормы будем опускать, например, k y _{aX a t}]| = ||y _{aX a t}]|_a .

Вычитая из уравнения (3.1) уравнение для нахождения ya-1, получим yatt + TAa yat + TAayatt = Уа-1#, а = 2,Р.

(3.3)

Здесь и далее в обозначении A _hα будем опускать h . Рассматривая уравнение для определения У 1 и y _p , из (3.1) находим

У1й ^{+ T}A 1 y 1t ^{+ T}A 1 У1й = f t ⁺ y ptt .

(3.4)

Умножим уравнение (3.3) скалярно на y _αtt :

kyatt II + т (Aa yat ,yatt) + T (Aa yatt, yatt)    (ya-1,tt, yatt) .

Так как

^{( A} a ^y at ^, y att ) — ^{( a} a y ax a t ^,

yaxatt] = ^ (aa,yaXat] t + 2 (aa,yaXatt] , то из (3.5) в силу положительности операторов Aa, а = 1,p, имеем

Wtiatt k2 + (aa,ya Xat] 6 (aa,ya Xat] + ^ya-1,ft^2 , aa = ka(x1,.

x a - 1 , x a

— 0.5 h a , X a+1 , . . . , X p ).

После умножения на τ просуммируем сначала (3.6) по j ⁰ от 2 до j:

jj

X kya^tk2 т 6 c2 kyaxattT+X Wa-1,й|2т, j 0=2j а затем по α0 от 2 до α:

jαj

E ky^t к2т 6 C2E kya ox at ]2t +e ky^ к2т.(3.7)

j0=2                 a0=2j

Умножив равенство (3.4) скалярно на y 1t_t , получим

0.5 k y 1tt k ² + т (A 1 y 1t ,y 1tt ) 6 0.5 к т f t + y ptt k ² .

(3.8)

Пользуясь формулой суммирования по частям и определением оператора A 1 , второе слагаемое в (3.8) запишем в виде

ТТ

Умножим (3.8) на т и просуммируем полученное неравенство по j 0 от 2 до j :

jj

X кУ1йк2т + (°1> (У1Х11)2] Т 6 (al, (yixit)2] Т + Т X Wf + ypttk2 10=2

или

X k j к ² Т 6 C 2 k y 1. 1 t к ² + Т X И + ■    ' , 0 < С 1 6 “ 2 6 C 2 .

j0=2

Так как

И + »рй\2 6 (тliftк + tall)2 = Т2kftII2 + 2Vtliftк • VTkypttk + \\ypttII2 6 Т2kftк2 + Тkftк2 + Тkypttk2 + kypttk2 = (1 + Т)Tkftk2 + (1+ Т)kypttk2, то из (3.8) после суммирования по j0 от 2 до j получаем jj

X ку1йк2т 6 cM^t ]i2 т+(1+т)т Xkfj'-1н2т j0=2

• (3.9)

• (3.10)

• (3.11)

1-1

⁺⁽ 1 ^{+ т ) т} Wp tt k ^{2 + (1+ т} ) 52 ^k y pPtt ^к 2 ^т-

1 ⁰ =2

Оценим последнее слагаемое (3.9) с помощью неравенства (3.7):

• 1                     p1

X WiPiX т 6 c2 X к»а xat]2 т+X ь»112 т-j^=2                а=2p

Из (3.9) с помощью (3.10) находим j0

52 курйк2т 6(1+т ) c2 52 к»а xat]i 2т 10=2

+ (1 + Т)т X kftP'-1112т + (1 + Т)тky-pitk2 + (1 + Т) X kyjitк2Т-0=2

Продолжая неравенство (3.11) вправо с помощью аналогичной процедуры, найдем jjp

L k y jt И ² Т 6 M l (T)( k y li, к ² + k y ps k ² + E k f P ^{0 - 1} k ² Т + E k » a...t l²),      (3.12)

P0=2                                              p0=2               а=1У где Mi(T) = сзТет, C3 = max(1,C2).

Из (3.7) и (3.12) следует j      jp

E k y a« к ² т 6 M 2 (t )( k y^ k ² + k y ptt k ² + e k f j ' ^{- 1} k ² т+ e k y ax aJ ²).      (3.13)

j ⁰ =2                                              j ⁰ =2               a=1          '

Так как из (3.6) при j = 1 следует

p

Htt II^{2 6} ^Х ^Et II^{2 +} Mtt II², a =2

то для получения необходимой оценки достаточно оценить Ну^ к и k y ax _{a t} ]l , а = 1,p. Для чего положим в уравнении (3.1) а = 1, j = 1. Тогда получим

Уш(т ) + TA i (y it (т) + y i_ft (T)) + Au i + A(u o + ти 1 ) = f (т).           (3.14)

Умножая (3.14) скалярно на yitt(т), находим lysll2 6 c2lluixi]|2 + Ilf(т) — Au1II2, U1 = uo + (1+ т)u1.            (3-15)

Из (3.6) с учетом (3.15) имеем pp

X k y a x a j ² 6 С ² E k y a _$<j ² +1     i^i k ² + k f (t ) - м n ²).      (3.16)

c 1                     c 1

a=2             a=2

Аналогично c помощью (3.14) оценивается и Hy^ t]\2. С помощью (3.15), (3.16) из (3.13) получаем j   jp

E k y a« k ² т 6 M (T)( E k f j ^{0 - 1} k ² т + E k u ix a k ² + k f (t ) - Au i k ²), а = 1^. (3.17)

j ⁰ =2                     j ⁰ =2              a=1

Из оценки (3.17) следует устойчивость разностной схемы (3.1)–(3.2) по правой части и начальным данным.

• 3.1.    Погрешность аппроксимации. Обозначим через z _a = y _a — u _a , а = 1,p, и

• подставим ya = za + ua в (3.1)-(3.2). Тогда для погрешности получим задачу αpα p

Z att + EA he Z e + Е A he Z e + E A he z et + E A he Z et = ^ a ,     (3.18)

в=1         e=a+1         в=1          e=a+1

Z a (0) = 0, Z at (0)= V 1 , а = 1, 2,...,p,                     (3.19)

где

αpα p

U att + E A he и в + E A he и в + E A he U et + E A he U et + f e=1         e=a+1         e=1          e=a+1       /

+ O( I h \ ² + т)+ f = O( I h \ ² + т),

• V 1 = ddtu (£) T = O(t ), 0 < £ < т , | h | = h l + h 2 + ... + h p O( | h | ² ) — погрешность аппроксимации оператора A. Кроме того, если u _a G C ⁴ [0, T], f(t) G C ² [0,T], то

• 3.2.    Сходимость разностной схемы. Для погрешности z _a = y _a — u _a оценка (3.17) принимает вид

(d^u            du e         л dueX    2x/\i\ⁱ2    x

t = —tda+ EAheit-+ EAheit^)+ O(|h| + т) +ft

\ в=1            в=1          /                               (3.20)

= — dt ⁺ f t ^{+ O ( | h | 2 + T} ) = ^{O ( | h | 2 + T} ),

C n [0,T] — класс функций, имеющий n производных, непрерывных по t на [0, T].

j   jp

X k j k ^{2 т} 6 M ( X k jr ^{т +} X k ^v ix a k ^{2 +}1Ш^т ) ⁺⁽ i ^{+ т ) Av} i k ²).     ( ³ -2i)

j 0=2               \^v=2           a=1                                   ²

Из оценки (3.21) с учетом (3.20) следует

Теорема. Пусть задача (1.1)-(1.2) имеет единственное непрерывное в QT реше-4      4        8       ∂2f ∂2f ние u(x,t) и существуют производные d-^, д4’ иди Г-’ df, df, a = 1,p, непрерывные в QT. Тогда схема (1.1)-(1.2) сходится со скоростью O(|h|2 + т) в норме kzk1 = (PP kjtt II2т

^X j 0 =2

1/2

4.    Волновое уравнение в релаксирующих средах

В цилиндре Q T рассмотрим задачу для волнового уравнения в релаксирующих средах

• d ² u

dtp + Lu = f (x,t), Lu = 22 L a U, (x,t) G Q t ,                (4.1)

a =1

u | s = 0, u(x, 0) = u o (x), u t (x, 0) = u 1 (x), X 1 ,X 2 = const > 0,         (4.2)

т _ Г d ²u । d d ²u । d ² d ² u 1

^где L a u = ^— ^dx a ^{+ X} 1 attax a ^{+ x} 2 dt p dx a] •

Структура третьего члена слева уравнения (4.1) такая же как у диссипативного члена в (1.1), описывающего затухания звука из-за вязкости и теплопроводности, четвертый член описывает слабые дисперсионные эффекты (см. [13, с. 87]).

Задачу (4.1)–(4.2) перепишем в виде абстрактной задачи Коши d2u               ,>du       ,>d2ud dtp + Au + x1Adt + x2Adt2 = f (t),  A = ^2Aa, Aa = — dx2 , a=1

u(0) = uo, ut (0) = u1.(4.4)

Вместо исходной задачи (4.3)–(4.4) запишем систему подзадач d2ua dt2

ppp

+ 52 Aeup + X1£ Aeupt + X2 ^Apuptt = f, a = ^p, в=1           в=1

u a (0) = u o ,   u at (0) = u 1 .

(4.6)

Как и выше, обозначим через z _a = u _a — и. Подставляя u _a = z _a + и в уравнение (4.5), получим

2p               pp

.,' + £ Aeze + XI £ Aezet + X2 £ Aezett = 0,(4.7)

β=1           β=1

Za(0) = Zat (0) = 0, a = 1,p.(4.8)

Умножив каждое из уравнений (4.7) скалярно на AadZa и просуммировав их по a = 1,p, получим p 2      pp         pp

∂ z _α     ∂z _α                      ∂z _α                         ∂z _α

(dt², A^a dt)⁺ 52 (52 A^e z^e, A^a dt )^{+ X} 1 52 ( 52 A^ez^e t , A^a dt )

a=1v            / a=1                  /     a=1 ^=1             / p / p                Я \                                          ( .

∂z _α

( £ Ae z ett , Aa "dt- ) = 0.

α =1 β =1

После интегрирования по частям в первом интеграле равенства (4.9) находим

p kzαxαt

α =1

p k2 + £Aa Za

2 ^t

+ 2X 1 / k A a z at II ²d^T +

p

χ 2      A α z αt

= 0.

pp  p

Откуда следует, что ^ A a Z a = Z A a Z at = IL A a Z att = 0, т. е. задача (4.7)-(4.8) α =1          α =1          α =1

принимает вид

∂ ² z

—a = 0, Z a (0) = Z at (0) = 0.                        (4.10)

Из (4.10) имеем, что для любого t Е [0,T], z _a (t) = 0 или, что тоже самое, u _a (t) = u(t), t Е [0,T], a = 1,p.

Покажем, что каждая из компонент вектор-решения непрерывно зависит от входных данных. Умножим уравнение (4.5) скалярно на A _a u _at , затем просуммируем их по a = 1,p. В результате получим

1 — XX II

2 dt ^k

II2     1 д uaxat 11 +2 dt

p

A α u α α =1

p

+ X 1     A a u at

χ 2 ∂

⁺ 2 dt

p

A α u αt  6

L k f k ^{2 +} =

p 2

A α u αt

α =1

(4.11)

Положив e = X21, затем проинтегрировав (4.11) по т от 0 до t, получим pp

£ kU ax _a t k ² + £Aa U a

+ X 2

p 2

A α u αt

α =1

6 ^X k f k 2,Q t + « u ix k ² + k Au o k ² + « AU 1 k ² ,

(4.12)

t kf k2,Qt = j kf k2 dT.

Из оценки (4.12) следует непрерывная зависимость решения задачи (4.5)–(4.6) от правой части и начальных данных.

5.    Разностные схемы

Для решения задачи (4.1)–(4.2) будем использовать векторную аддитивную схему

αp   α   p

• y a±t + ^A e y e ⁺ 52 A e y e ⁺ x i 52 A e y et +x i 52 A e y et

в=1         в=а+1           в=1            в=а+1

(5.1)

αp

+X2 52 Ae yett+X2 52 Ae yett = f, в=1            в=а+1

У а (0) = U 0 ,   y at (0) = U 1 .                                 (5.2)

Задача (5.1)–(5.2) недоопределена. Для применения этой схемы требуется задать еще одно условие, например, значение y _a (t) на втором слое у _а (2т ).

Будем искать у _а (2т ) из соотношения

и(2т ) — 2и(т ) + u(0) т ²

= du ^{( т ) + О ( т 2 )} -

Определим ddtu (т) из уравнения (4.1), положив t = т . Тогда получим задачу для определения v = du (x,T)

Av--v = F, v | r = 0,                               (5.3)

X 2

^{d 2} u/          ^d2^й/             ^du

X 2

f 1 дЦ   ) + A dxj

Так как X2 > 0, то задача Дирихле (5.3) однозначно разрешима.

Итак, будем считать, что задача (5.1)–(5.2) дополнена еще одним условием yatt = U2 или Уа(2т )= U2, U2 = U0 + 2U1T + U2 T2.

Умножим (5.4) скалярно на y_αtt:

kyatt k ^{+ т(}Aa^yat, ^yatt) ^{+ X}1^T(Aayatt, yatt)^{+ X}2^T(Aayattt'yatt)   ^(ya—1.tt, yatt^).

Откуда с учетом вида операторов Aα находим kyattk2 + kyaxat ]|2 + x2kyaXatt]|2 6 kyaXa t]|2 + x2 kyaXatt ]I2 + ||ya-1,tt^ .

Просуммировав (5.5) сначала по j0 от 3 до j, а затем по s от 2 до а, получим jα    αj

X l|yaftk2T 6 X kysXst(2T)]l2T + Х2 X ||ysxst"t(2T)]12т + X kyjttk2T.

j0=3             s=2 s=2

Рассматривая уравнения для определения y1 и yp из (5.1), получаем равенство yut + TA1 y1t + X1TA1y1it + X2TA1y1ttt = Tft + yptt.(5.7)

Из (5.7), как и выше, с помощью (5.6) получаем послойную оценку

^X 16 (1 + T) X kyaxat(2T)12T + (1 + T)X2 X Цу»»(2т)]|2т 10=3                    a=1                             a=1

+ (1 + т) X Hilak²T + (1 + T)т X 1 Vт + (1 + т)т |У1_Й(2т)k². 10=3                          10=3

(5.8)

Продолжая неравенство (5.8) вправо, находим

^Xllj-к²т 6 M(T) Н|У1й(2т)k²+ ||у_рй(2т)||² l⁰=3

j0p                           p

⁺X Ilf-¹'-^{1|2т +}X 11УаХа-^(2т)]|^{2 +}Х2 X ||УаХа-"-^(2т)]|²

10=3              a=1                    a=1

(5.9)

Из (5.6) и (5.9) получаем оценку

1₂                                                              1

E kyat-k2т 6 M(T)(кУ1«(2т)k2 + kyp«(2т)k2 + £ kf1'-1k2т f=3                                                1=3                   (5.10)

pp

■ X ||Уох а-^(2т)]|^{2 +}X baxай^(2т)]П .

a=1               a=1

Так как из (5.5) следует

pp

^||УрЙ^(2т)l|^{2 6}X WyaSa-^(т)]l^{2 +}X2 X ^kyaXat-⁽T^)]l2 ⁺||У1Й^(2т)k2 ,         (5-¹¹)

a=2                a=2

то для получения необходимой оценки достаточно оценить |У1й(2т)k, l|y_ax_a-(2т)]|, ^кУай_а^й(2т)]|, ^а    1,p.

Для этого положим в (5.1) а = 1, j =2:

p

У1й^(2т) ^{+ А}1У1^(3т) ■ X Ae У в^(2т) ⁺Х1^А1У1-^(2т)

в=2

pp

+Х1 X AeУв-^(т) ⁺X2A1У1Й^(2т) ⁺Х2 X AeУвй^(т) = ^{f (2т}).

в=2                              в=2

(5.12)

Из (5.11) следует

У1Й (2т) + тА1 У1-(2т) + тх1 A1 У1й (2т) + тх2 A1 У1й-"(2т) = F (2т),        (5.13)

где F(2т) = f (2т) - AU2 - X1A(u1 + ти2) - Х2AU2.

Из (5.12) следует

1У1й(2т)k²6 |У1Х1-(т)]²+ X2ky1xiй(т)]²+ kFk².

(5.14)

Аналогично из (5.5) получаем оценки ppp

52 llyaXat(^2T)]|^{2 6} 52 kyaXat^(т)]|^{2 +}X2 52 kyaXatt(^T)k^{2 +}1|У1й(^2т)k²,          (5.15)

a=2               a=2

P                          1 P                       P1

52 kyax_ait^(2T)]l^{2 6}— X l|yax_at^(T)]|^{2 +}X hal^t^(t)k2 ⁺ —bitt^(2т)k2•      ⁽⁵-¹⁶⁾

ααα a=2                X2 a=2              a=2

Нормы kyix1t(2т)]|, ||У1Х1й]| оцениваются с помощью равенства (5.7). С помощью оценок (5.11), (5.14)–(5.16) из (5.10) окончательно получим jjp

X kyattk2т 6 M( X kft'-1k2т + X kuixa + u2Xaтk2 j 0=3                 ^j0=3

(5.17)

p

+ X ku2xaH ²+ kf (2т) - Au2 - X1 A(u1 + TU2) - X2AU2 k² a=1

Из (5.17) следует устойчивость схемы (5.1)–(5.2) по правой части и начальным условиям, а при достаточной гладкости решения исходной дифференциальной задачи сходимость схемы (5.1)-(5.2) со скоростью O(|h|²+ т). Условия гладкости на u(x,t) здесь те же самые, что и в теореме из пункта 3.2.

6.    Модифицированное уравнение влагопереноса

В цилиндре QT рассмотрим уравнение влагопереноса Аллера

∂u dt = Lu + f (x, t), Lu = 52 Lau, x ^ G, t ^ (0, T],

(6.1)

u|sT = 0, u(x, 0) = uo(x),(6.2)

где Lau = dl2 (ka^(x)dXa) ⁺Itdl- (ka^(x)?£) ’ ^a = ^1,P, ⁰< c1 ⁶ka^{(x) 6}c2•

Задачу (6.1)–(6.2) перепишем в виде абстрактной задачи Коши

• — + Au + A-Д" = f (t), A = ^2 Aa, Aa = - д  fka(x)    ^ ,

dt          dt                               ∂xα a=1

u(0) = Uo.(6.4)

Введенный Аллером (см. [8]) дополнительный член χ _∂^∂_t^∂_∂²_x^u₂призван объяснить опытный факт движения влаги против градиента влажности. Коэффициент Аллера χ мал при впитывании влаги и велик при испарении (см. [12, с. 159]). Мы включаем это слагаемое в уравнение в виде (k_a(x)ux)_lt, a = 1,p.

Вместо задачи (6.3)–(6.4) запишем систему подзадач:

du_α dt

pp

+ 52 Ae ue + E Ae uet = f (t), e=1        e=1

u_a(0) = uo, a = 1,p.

• (6.5)

• (6.6)

Очевидно, что U_a(t) = u(t), и поэтому в качестве решения исходной задачи (6.5)-(6.6) можно взять любую компоненту вектора U(t) = (ui(t),..., up(t)).

Для решения задачи (6.5)–(6.6) справедлива оценка p              p

£ kUatk²+ £Aa

uα

a=1

6 M(kfII²+ kAuok²).

(6.7)

Из (6.7) следует непрерывная зависимость решения задачи (6.5)–(6.6) от входных данных в норме, стоящей в левой части оценки (6.7).

Каждую задачу (6.5)–(6.6) заменим разностной схемой

αpαp yat + EAye + E Aeye + E Aeyet + E Ae= f,(6.8)

в=1        в=а+1        в=1

ya (0) = Uo, a = 1,p.(6.9)

Следует заметить, что задача (6.8)–(6.9) недоопределена. Для применения этой схемы требуется задать еще одно условие, например, значение y_a(t) на первом слое y_a(T). Будем искать y(x, т) из соотношения

'          = du (x, 0)+O(T).

τ∂t

Значение du|t=o ищем исходя из дифференциального уравнения (6.1)

ди             д Д . . du0(x)\   х д . д ,.

TT? = £ я  ka (x)^--- + £ я  ka (x) д U- (x, 0) + f(x, 0), dt          dxa V       dx )       dxa V     dxa/ t=o a=1

или

p

- £ (ka(x)U1xa)xa + U1(x) = F(x), U1 (x)|r = 0,                (6.10)

a=1

где

p

F(x) = f (x, 0) + £ (kaUOxa)xa, U1(x) = Ut(x, 0).

a=1

Итак, будем считать, что задача (6.8)–(6.9) дополнена еще одним условием yat(0) = U1 (ya(T )= Uo + TU1 = U1), a = 1,p.                (6.11)

Применяя тот же прием, что и выше, получаем априорную оценку для решения разностной задачи (6.8)–(6.9), (6.11):

j   jp

E kyatk²T 6 M ( E kfj^0-1k²+ E I"1-al²+ kyOtf (T) - AU11² ),      (6.12)

j⁰=2                 j⁰=2             a=1

где U1 = (1 + t) U1 + Uo, M — положительная постоянная, не зависящая от hi, i = 1,p, t.

Из оценки (6.12) следует устойчивость разностной схемы (6.8)–(6.9), (6.11) по правой части и начальным данным. Из этой же оценки следует сходимость решения разностной задачи (6.8)–(6.9), (6.11) к решению дифференциальной задачи (6.1)–(6.2) со скоростью O(|h|²+ т) при тех же условиях гладкости на U(x,t), что и в теореме пункта 3.2.

Завышение гладкости u(x, t) в рассматриваемых задачах объясняется присутствием в априорных оценках для погрешности z_a= y_a— U_a, a = 1,p, разностной производной от погрешности аппроксимации ^(j.