Векторные поля с нулевым потоком через сферы фиксированного радиуса
Автор: Волчков Виталий Владимирович, Волчкова Наталья Петровна
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 4 т.20, 2018 года.
Бесплатный доступ
Классическим свойством периодической функции на вещественной оси является возможность ее представления тригонометрическим рядом Фурье. Естественным аналогом условия периодичности в евклидовом пространстве Rn является постоянство интегралов от функции по всем шарам (или сферам) фиксированного радиуса. Функции с указанным свойством можно разложить в ряд по собственным функциям оператора Лапласа специального вида. Этот факт допускает обобщение на векторные поля в Rn, имеющие нулевой поток через сферы фиксированного радиуса. При этом для них возникает представление Смита в виде суммы соленоидального векторного поля и бесконечного числа потенциальных векторных полей. Потенциальные векторные поля удовлетворяют уравнению Гельмгольца, связанному с нулями функции Бесселя Jn/2. Целью данной работы является получение локальных аналогов теоремы Смита. Изучаются векторные поля A с нулевым потоком через сферы фиксированного радиуса на областях O в евклидовом пространстве, инвариантных относительно вращений...
Векторное поле, нулевое сферическое среднее, сферическая гармоника, функция ломмеля
Короткий адрес: https://sciup.org/143168778
IDR: 143168778 | УДК: 517.444 | DOI: 10.23671/VNC.2018.4.23384
Текст научной статьи Векторные поля с нулевым потоком через сферы фиксированного радиуса
Естественным аналогом условия (1) в многомерном случае является постоянство интегралов от функции по всем шарам фиксированного радиуса. Близкий класс функций получается, если здесв заменить шары на сферы фиксированного радиуса.
Согласно теории рядов Фурье всякую T-периодическую функцию f G C 1 (R) можно разложить в абсолютно и равномерно сходящийся тригонометрический ряд
„ ч ao , /2пт 2пт f (x) у ■ zL am cos I ^Tx x + bm sin I ^Tx x , (2)
m =1
a0
-
t. e. представить f в виде суммьi константы — и последовательности периодических функций {fm}^=i, удовлетворяющих дифференциальным уравнениям
fm (x) + —^fm(x) = 0.
m T2
Существенно более трудной задачей является описание функций с постоянными интегралами по шарам (или сферам) фиксированного радиуса. Для эффективной характеризации указанных классов требуется привлекать соответствующие специальные функции. Например, в двумерном случае имеет место следующий результат.
Теорема А. Пусть f G C “(R2). Тогда функция f имеет нулевые интегралы по всем кругам в R2 рад нуса r в том и только том случае, когда имеет место разложение
∞∞ m f (х,У)= ^ ^ cq,mJm (^ V Х2 + У2) I , 2 ) , m=-^ q=1 Vr x + У2
гДе Jm ~ функция Бесселя порядка m, {vq}q=i — последовательность всех положительных нулей функции Ji, занумерованных в порядке возрастания, и коэффициенты cq,m G C удовлетворяют условию cq,m
-о (У
при q — то
для любого фиксированного a > 0. Отметим, что функции
—) - Jm ( ^ VX2+72 ЯдА Г k r ; 7x2 + y2
являются собственными функциями оператора Лапласа Ав R2. Подобные результаты были получены и для функций меньшей гладкости, заданных на ограниченных множествах в Rn, n > 2, инвариантных относительно вращений (см. [1, теорема 3], [2, теорема 3], а также [3-5], где содержатся существенно более общие результаты, касающиеся структуры решений уравнений в свертках).
Гораздо менее изученным в этой области является случай векторных полей. Если рассматривать f G C 1(R) как векто}:шое поле в R. то условие
f(x - У - f(x+т)=0
означает, что f имеет нулевой поток через любую нульмерную сферу радиуса T/2. Таким образом, равенство (2) дает представление для полей с нулевым потоком через все сферы радиуса T/2 в R1. Этот факт допускает нетривиальное обобщение на векторные поля в Rn. При этом константа 00 интерпретируется как соленоидальное векторное поле, a {fm} заменяются на потенциальные векторные поля, удовлетворяющие уравнению для собственных функций оператора Лапласа. Указанное утверждение является частным случаем следующего локального результата Д. Смита [6, теорема 3].
Теорема В. Пусть A : Br+i ^ Rn (1 < R ^ то) — вектор ное поле в Rn класса C n+a (0 < а < 1), имеющее нулевой поток через любую сферу единичного радиуса, лежащую в Br+i. Тогд а для x Е Br имеет место равенство
∞
A (x) = As (x) + ^ Am(x), (з)
m=1
в котором ряд сходится равномерно на компактах из Br, A s — соленоидальное векторное поле класса Cn+a и Am — потенциальные векторные поля, удовлетворяющие уравнению
(А + vm ) A m = 0 , (4)
где {vm}m=i — последовательность всех п<)ложителы1ых нулей функции Jn/^. занумеро ванных в порядке возрастания.
Символ Br в теореме В н ниже обоз!тачает открытый шар it; Rn рад:iyca R с центром в нуле. Класс Cn+a определяется как класс таких функций f Е Cn, у которых частные производные порядка n удовлетворяют условию Гёльдера с показателем а. Напомним также, что векторное поле A = (Ai,...,An) класса C1 в области D С Rn называется соленоидалъннм, если
л- а \Г dAj div A := ) —— ∂x j=i j
=0
во всех точках области D, и потенциальным, если существует скалярное поле u в D такое, что
∂u ∂u
A = gradu := -—,..., -— . dxi dxn
Одним из существенных недостатков теоремы В является отсутствие разложения (3) во всем шаре Br+i. Это создает серьезные препятствия для изучения свойств векторного поля A на всей области определения. Кроме того, метод доказательства теоремы В не позволяет получить подобное описание для областей вида
Ва,ь = {x Е Rn : a < |x| < b} •
В данной работе предложен иной подход, позволяющий преодолеть перечисленные выше трудности. В теоремах 1, 2 ниже получено полное описание векторных полей в шаре и шаровом слое пространства Rn, имеющих нулевой поток через границу любого шара фиксированного радиуса, лежащего в этих областях. Отметим, что при этом возникают новые специальные функции (гипергеометрическая функция порядка (1, 2) и функции Ломмеля), которые не появлялись ранее в подобных задачах для евклидова пространства.
-
2. Формулировки основных результатов
Пусть r > 0 фиксщюваио. x Е Rn.
Br(x) = {у Е Rn : |x - y| < r},
Br (x) 11 dBr (x) — соответственно замьшаппе ii тратта шара. Br (x).
Для области O С Rn. содержалщй шары B r (x) при шлкоторых x. обозначим через: V r (O ) совокупность всех iienpeiзывных векторных полей A : O ^ Rn с условием
У A • nd£ = 0 (Vx e Rn : Br(x) С O), dBr (x)
где n — единичный вектор вне шпей нормали к Гранине dB r (x) d^ — элемент пл отпади на. dB r (x).
Далее, как обычно, Sn-1 — единична я сфера из Rn с центром в нуле, Hk — пространство сферических гармоник степени k на S n-1. Пространство L2(S n-1) является прямой суммой попарно ортогональных пространств Hk, k = 0,1,... (см., например, [7, гл. 4, § 2]). Пусть d k — размерность Hk, {Y^k)}^i — фиксированный ортонормированный базис в Hk- Для тонки x e Rn положим
Р = Ixl, a = |x|, x = 0-
(k)
Функция Yv 7 продолжается до однородного гармонического многочлена степени k в Rn по формуле
Y/k)(x) = pk Y/k)(x).
Если область O инвариантна отпосителыто вращений пространства Rn. то всякой локально суммируемой в O функции f соответствует ряд Фурье вида
∞ dk f (x) = E Efk,i(P)Y(k)(a), k=0l=i где _______ fk,l(p) = j f (pa)Yl(k)(a) da
Sn-1
Разложение функции Бесселя порядка v e R в степенной ряд имеет вид
J v (t) =
(И
=
(-1)m m!r(v + m + 1)
r-
где Г — гамма-функция. Функция Неймана порядка v e R выражается через функцию
Бесселя по формуле
Nv (t) = lim
µ→ν
J^(t) cos(n^) - J-^(t) sin(n^)
Пара {Jv, Nv} является фундаментальной системой решений дифференциального уравнения Бесселя t2d2U + tdu + (t2 - v2P = 0. dt2 dt
Обозначим через iF2(ai; bi,b2; t) пшергеометрическую (функцию порядка (1, 2). определяемую равенством iF2(ai;bi,b2; t) = E (b^k, № где
(а) о = 1, (a)k = a(a + 1)... (a + k — 1), k = 1, 2,...
(см., например, [8, гл. 4]). Присоединенная функция Ломмеля с индексами ц, v G R определяется равенством
dt2 dt
Следующие результаты дают описание гладких векторных полей A, принадлежащих классам Vr (Br) и Vr(Ba,b) соответственно.
Теорема 1. Пусть r > 0, r < R С +то, A : Br ^ Rn — векторное поле класса C“. Тогда A принадлежит Vr (Br) в том и только том случае, когда
A(x) = As(x) + B(x)x, x G Br,(8)
где As — соленоидальное векторное поле класса C^. B — скалярное поле, коэффициенты Фурье которого представимы рядами
BkM = £ Ym,k,i Pk 1 F 2 (n+^; n+k +1, n + k; — (^A 0 c p < R,
2 2 22r m=1 x7
в которых константы ym k i убывают быстрее любой фиксированной степени vm при m ^ то.
Здесь и далее B(x)x — векторное поле, определяемое равенством
B(x)x = (B(x)x i , . . . , B(x)xn).
Теорема 2. Пусть r > 0,0 С a < b С +то, b — a > 2r, A : Ba,b ^ Rn — векторное поле класса C“. Toгда A принадлежит Vr(Bab) в том и только том случае, когда
A(x) = As(x) + B(x)x, x G Ba,b, где As — соленоидальное векторное поле класса C^. B — скалярное поле, коэффициенты Фурье которого представимы рядами
∞
Bk,l(p) = £ -m-T [( n + k — 2)J2 + k- 1 (“ p) S2- 1 ,n + k-2 (-mp) — m =1
—
J2 + k-2 (vp) Sn,2 + k- (t p) ] +
+
βm,k,l pn-1
[ ( n+k—2)N n + k- i v m 1 p) S n - i , 2 + k- 2 (-rmp) —
—
N2 + k-2 (^mp) SП,П + k-1 (^mp) ] +
γm,k,l ρn ,
a < ρ < b,
в которых константы am^j, em,k,h Ym,k,l убывают быстрее любой фиксированной степени vm щ )п m ^ то.
В отличие от теоремы В теоремы 1, 2 дают разложение для полей A из рассматриваемых классов на всей области определения. Отметим также, что теоремы 1, 2 являются развитием результатов В. В. Волчкова об описании функций с нулевыми интегралами по сферам фиксированного радиуса на случай векторных полей (см. [1, 2], а также [3-5]).
-
§ 3. Вспомогательные утверждения
Прежде всего напомним некоторые свойства встречающихся выше специальных функций.
Для функций Бесселя и Неймана справедливы следующие формулы дифференцирования [8, гл. 7]
|
dt (tv J v (t))— tv Jv-1(t), |
ddt (tv N v (t)) |
— tv N v -1(t), |
(9) |
|
d ( J v (t) A — — Jv+1(t) d / N v (t) \ — — Nv+1(t) dt V tv ) tv ’ dt\ tv ) tv • Отметим следующие свойства функций Ломмеля [9, приложение II, § 11.12]: |
(10) |
||
S^,-v (t) — S^,v (t),1Д1)
S^(t) — t^-1 + (v2 - (p - 1)2) S^—2,v(t),(12)
2vS^,v(t) — (p + v — 1)tS^-1,v-1(t) — (P — v — l)tS^-1,v+1(t),(13)
dtS^v (t) — "tS^,v (t) + (p — v — l)S^-1,v+1(t)-(14)
Из (14) имеем dt (tvS^,v(t)) — v tv 1S^,v (t) + tv ( tS^^V (t) + (p — v — l)S^-1,v+1(t))
— tv 1 (2vS^,v(t) + (P — v — 1)tS^- 1 ,v +1 (t)) •
Отсюда и из (13) получаем dd (tvS,,v(t)) — (p + v — 1)tvS^-1,v-1(t).
Лемма 1. Для функции h(t) — 1F2(a; a + 1,в; Yt) имеет место соотношение th’(t) + ah(t) — аГ(в)
Je- 1 ^V—Tt)
/----7 e- 1
-γt
<1 Из (6) ii on ределеиия h имеем
ДД (a)ka (Yt)k ah(t) — Ю (a + 1)k(e)k ,
‘ v^ (a)k k(Yt)k
.
() k = 0 (a + 1)k(в)к k!
Складывая эти равенства и учитывая, что получаем
(a)k
(a + l)k
(a + k) = a,
th‘(t)+ ah(t) = a £ k=0
1 (Yt)k (в) к k!
Теперь используя разложение
J v (t) =
r(v + 1)
t v V 1 (-t2/4)k
2 k =0 (v + 1)k k!
(cm. (5)), приходим к требуемому утверждению. >
Лемма 2. Имеют место равенства
((р + V - 1)tJ v (t)S ^ -1 ,v -1(t) — tJ v -1(t)S ^,v (t) ' = J (t), ( (p + V - 1)tN v (t)S ^ -i ,v -i(t) - tN v -i(t)S ^,v (< = t ^ N v (t).
<1 Используя (9), (11) и (15), находим ddt(J(t)S^—1,v—i(t)) = ddt (tvJvW"-S,—i,i—v(t))
= tJ v -1(t)S ^ -i ,v -1(t) + (p - v - 1)tJ v (t)S^- 2 ,v (t).
Далее, с помощью (10) и (15) получаем ddt(tJ„-1(t)S„.„(t)) = dt (t1-vJv-1(t)tvS^(t))
= -t J v (t') S p,,v (t) + (P + v - 1)tJ v -1 (t)S^- 1 ,v- 1 (t)-
Исключая из правых частей этих соотношений функцию tJv-1(t)Sp,— 1 , v-1(t), имеем
4 ( tJv- 1 (t)SM,v(t) ) = -tJ v (t)S ^,v (t) + (p + V - 1) -d (tJ v (t)S^- 1 ,v- 1 (t) ) dt dt
+ ( v2 - (p - 1)2 ) tJv(t)S^- 2 ,v(t).
Отсюда и из соотношения (12) следует формула (16). Равенство (17) доказывается аналогично. >
Лемма 3. Пусть скаля]люе поле B Е C 1 (0) имеет вид
B (x) = y(p)Y(k)(a). (18)
Тогда.
div(B(x)x) = ( р^‘(р) + ny(p) ) Y(k)(.y).
< Для любого ока.тяриого поля B Е C 1(0) имеем n ∂ n ∂B n ∂B div(B(x)x) = У^ ——(xjB (x)) = y^B(x) + Xj = nB (x) + ^^Xj .
∂xj ∂xj ∂xj j=1 j=1 j=1
Пусть теперь выполнено условие (18). Запишем B в виде
B(x) = ^(p)Yi(k)(x), ^(р) = ^^.
Тогда дв /(p) (k) dY (k)(x)
— =----xjY/ 'xc) + ф(р).
∂xj ρ lxj
Следовательно, div(B(x)x) = n^(p)Yl(k\x) + ^ ^-^xjY^k(x) + ^(p) ^Xj9 l (X j=i p j=i
" dY (k)(x)
= (n^(P) + ^ (р)р) Y1 (x) + W ^ Xj^7T• ∂x j=1
Поэтому по теореме Эйлера об однородных функциях div(B(x)x) = ((n + k)^(p) + ^‘(p)p) Y(k)(x).
Поскольку
^(p = Уф - t*>, pk pk +1
отсюда вытекает требуемое равенство. >
Из леммы 3 непосредственно получаем следующее утверждение.
Следствие 1. Имеет место равенство
Y (k)(Y div l—— x = 0.
ρn
Следствие 2. Пусть n + k n + k ri vmp\2X
*W = p k i F2 (2; — + 1, ^ + k;- (^) ) .
Тогда div ^^(p)Yl(k)(ct)x^ = (n + к)Г (n2 + k) 2n +k-1
X ^-rm )1-k-n p1-n Jn +k-i ^rmp) y <1 Полагая n + k n + k n ,v2 a(t) = 1F-(—; —+ 1,2 + k;- 4m t). получаем ^(p) = pk ^(p2) 11 p^‘(p) + n^p) = pk (2p2^‘(p2) + (n + k)^(p2)).(22) По лемме 1 имеем t-W) + (Ц^ W) = (n^ Г (n + k) 22+k-1 J m. (23, 2 2 42 7 vmpp) 2 +k 1 Комбинируя (22), (23) и (19), приходим к (21). > Следствие 3. Пусть рМ = [(n + k - 2)Ji+k-i (pmp) Si-1,i+k-2 (pmp) vm vm 1 — Ji +k-2 -p S 2,2 +k-l -p pn-1 - Тогда. n div (y(p)Yl(k)(a)x) = (^m) i p1-iJi+k-i (^mp) Yl(k)(CT). <1 Используя формулу p^'M + np(p) = pn-r (p^WW и лемму 2 при v = П + k — 1, д = 2, находим p^(p)+ np(p) = pn-1 [(n + k — 2)--pJn+k-1 r2 νm νm ( Vp7 Sn-1n+k-2 (Tp7 vm vm vm ‘ r vm i 1- n vm -—pJn+k-2(—p)Sn,n+k-i(vdJ vm = 1 v) p iJn+k-1(Tp)- Отсюда и из леммы 3 получаем требуемое утверждение. > Аналогично доказывается Следствие 4. Пусть p(p) = [(n + k — 2)Nn+k-1 (^mp) Sn-1,n+k-2 (m1 p) — Nn+k-2 (Vmp) Sn,n+k-1 (vmp)] pn^. Тогда. n div (p(p)Yi(k)(^)x) = (pm) 2 p1-iNn+k-1 (pmp) Yi(k)(CT-. Лемма 4. Пусть A E C 1(Ba-ib), po — фиксированное 1шсло из интервала (a, b), и A (tx)~tn 1dt, a < |x| < b. Тогда. div (B(x)x) = A(x). <1 Прежде всего отметим, что определение функции B является корректным. Действительно, если a < |x| С ро, то 1 С рО и при 1 С t С р)0 выполнены неравенства a < |x| С t|x| С ро < b. Аналогично, если ро < |x| < b. то РО < 1 и и ри РО С t С 1 имеем |x| |x| a < Ро С t|x| С |x| < b. Далее, по формуле Лейбница находим ∂B ∂xj ∂ ∂xj A(tx1,... ,txn)tn 1dt ро(Д + -+Д)-1/2 = -A(tx>tn-1U/Hdx; (я)+ / dxj(A(tx)) tn-1 dt ρ0/|x| n-1 1 = -A (РтНп) Р0Mxj + TT (A(tx)) tn-1dt |x| 7 \|x| |x|3 dxj ρ0/|x| = A (lx") №+2xj + i dj(A(tx)) tn 1 dt‘ ρ0/|x| Отсюда (см. (20)) div(B(x)x) = nB(x) + 5 xjdB = n j A(txr1 dt + 5 A (pxx) |xpР+ xj j-1 ро!\х\j + / ρ0/|x| d ^xj—— (A(tx)) tn1 dt = n A(tx)-t1dt ∂xj j-1 Po/\x\ n 1 / n +A (Txr) (Я) + / tn (? xj dxj(tx)) dt‘ P0/\x\ V-1/ Преобразуем последний интеграл с помощью формулы интегрирования по частям. Тогда 1n I tn (5 P0/\x\ м 1 xj lAj(tx) dt = [ -d (A(tx)) tn dt dt ρ0/|x| tnA (tx) ρ0/|x| -n j A (Wn-1 dt. ρ0/|x| Используя это соотношение и (25), получаем равенство (24). > Лемма 5. Пусть A Е C 1(Br) и B(x)=/ Aw-1 dt, 0 |x| < R. 4. Доказательства теорем 1 и 2 Тогда. div (B(x)x) = A(x). <1 Утверждение леммы 5 получается теми же рассуждениями, что и в доказательстве леммы 4. > Приведем два известных результата (см. [1, 2]), которые потребуются ниже. Лемма 6. Пусть r > 0. r < R С +to. f Е C^(Br). Тогда (}>упкцпя f имеет нулевые интегралы по всем замкнутым шарам радиуса г, лежащим в Br в том и только том случае, когда при всех целых k ^ 0, 1 С l С dk имеют место равенства ∞ fk,l(P) = Р1-n ^ cm,k,l Jn+k-i (mpp) , 0 С P < R, m=1 где Cm,k,i Е C II k = O Cm) при m ^ to для любого фиксированного a > 0. Лемма 7. Пусть r > 0,0 С a < b С +to, b — a > 2r, f Е Cю(Ва,ь). Тогда функция f имеет нулевые интегралы по всем замкнутым шарам радиуса г, лежащим в Ва ь в том и только том случае, когда при всех целых k ^ 0, 1 С l С dk имеют место равенства ∞ fk,l(p) = Р1-2 УС am,k,l Jn +k-1 m=1 (VmP) + вт,к,1 Nn+k-1 (^P) , a < ρ < b, где am,k,i Е C вт,к,1 Е C ii |am,k,l| + |em,k,l| — O νmα при m ^ TO для любого фиксированного a > 0. < Доказательство tеорем 1 и 2. Пусть A Е Vr(Br) n C^(Br). По (формуле Гаусса — Остроградского имеем J Br (x) div A (y) dy -J dBr (x) A • n d^ = 0 (Vx Е Br-г), где n — eoiiiiirnibni вектор виешиoil нормали к грашще шара Br(x). Это означает, что (рункпня div A имеет иулеввю шгтегралв! по в<-ем 'замкнутым шарам радиуса г. лежащим в Br. Отсюда по лемме 6 ∞ νmρ , (div A)k,l(P) = Р1-n УС cm,k,lJn +k-1 m=1 где константы cm,k,i убывают быстрее любой степени vm пр и m ^ то. Рассмотрим векторное поле C(x) = B(x)x. где B(x) = У о div A(tx)tn-1 dt. Тогда Bk,i(p)= j Sn-1 В^рФ^^Ф) da S 1 / о div A(tpa)tn 1 YfkH^ da div A^payY^k(a) da tn-1 dt = j (div A)k,i(tp)tn-1dt. о Теперь в соответствии с (27) Bk,i(p) = / р12: cm,k,iJn+k—1 (t^m- ) t n dt-=1 r о Используя формулу x , av A + v + 1 A + v + 3 a2 A / Jv(at)t dt = 2-. ■ 1F2 ( 2 ; 2 ’v +1; — z) ’ о Re(A + v) > —1 (cm. [11, n. 1.9.1, формула 1]), получаем »Ыр) = E YmAl Pk 1F (n^; n^ + 1, n + k; — (^)2) , 22 22r m=1 x7 где = __________cm,k,l__________ / vm) 2 +k-1 Ymkl - (n + к)Г (2 + k) 22+k-1 Кроме того, по лемме 5 divC = div A. Полагая As = A — C, из (28) и (29) получаем представление (8). Обратное утверждение теоремы следует из соотношений (21), (26) и леммы 6. Таким образом, теорема 1 доказана. Повторяя теперь рассуждения выше с использованием следствий 1, 3, 4 и лемм 4, 7, получаем утверждение теоремы 2. > В заключение выпишем явное разложение полей bmkAx) = P1F2 (ni^k; ni^k + 1,2 + k; — (vr-)2) YlW(a)x. возникающих в теореме 1, в виде суммы соленоидальной и потенциальной части, удовлетворяющей уравнению вида (4) из теоремы В. В силу равенства (21) и [3, ч. 1, гл. 5, формула (5.27)] имеем A div bm, k^(x) = - (т) div bm,k,l(x). Отсюда и из равенства A = div grad находим div (grad divbm,k,i(x) + ^уbm,k,i(x)^ = 0. Кроме того, A grad div bm,k,i(x) = grad A div bm,k,i(x) = - ( Vm ) grad div bm,k,i(x). Поэтому искомые соленоидальная и потенциальная части равны И bm,k,i (x) + r Vm) grad div bm,k,i(x) - r Vm) grad div bm,k,i (x) соответственно.
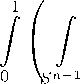
Список литературы Векторные поля с нулевым потоком через сферы фиксированного радиуса
- Волчков В. В. Окончательный вариант локальной теоремы о двух радиусах//Мат. сб. 1995. Т. 186, № 6. С. 1534.
- Волчков В. В. Решение проблемы носителя для некоторых классов функций//Мат. сб. 1997. Т. 188, № 9. С. 13-30 DOI: 10.4213/sm255
- Volchkov V. V. Integral Geometry and Convolution Equations. Dordrecht: Kluwer Acad. Publ., 2003. 454 p.
- Volchkov V. V., Volchkov V. V. Harmonic Analysis of Mean Periodic Functions on Symmetric Spaces and the Heisenberg Group. London: Springer-Verlag, 2009. 671 p.
- Volchkov V. V., Volchkov V. V. Offbeat Integral Geometry on Symmetric Spaces. Basel: Birkhauser., 2013. 592 p.
- Smith J. Harmonic analysis of scalar and vector fields in Rn//Math. Proc. Cambridge Philos. Soc. 1972. Vol. 72, № 3. P. 403-416 DOI: 10.1017/S0305004100047241
- Стейн И., Вейс Г. Введение в гармонический анализ на евклидовых пространствах. М.: Мир, 1974. 332 с.
- Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. Т. 1, 2. М.: Наука, 1973, 1974. 296 с.
- Прудников А. П., Брычков Ю. А., Маричев О. И. Интегралы и ряды. Дополнительные главы. М.: Наука, 1986. 800 с.
- Коренев Б. Г. Введение в теорию бесселевых функций. М.: Наука, 1971. 287 с.
- Прудников А. П., Брычков Ю. А., Маричев О. И. Интегралы и ряды. Специальные функции. М.: Наука, 1983. 750 с.


