Верхние оценки сложности дополнительных пространств некоторых кружевных узлов

Пусть M - компактное трехмерное многообразие с непустым краем. Напомним [1], что подполиэдр P ( M ) называется спайном многообразия M , если многообразие M \ P гомеоморфно ( M х (0,1]). Спайн P называется почти простым, если линк каждой его точки вкладывается в полный граф K 4 с четырьмя вершинами. Точки, линки которых гомеоморфны графу K 4 , называются истинными вершинами спайна P . Сложность c ( M ) многообразия M определяется как минимальное возможное число истинных вершин почти простого спайна многообразия.

Табулирование трехмерных многообразий заданной сложности и получение точных значений сложности для больших классов многообразий дают естественный подход к проблеме их классификации. Задача вычисления сложности многообразий является весьма трудной. К настоящему времени точные значения сложности известны только для конечного числа табулированных многообразий [2, 3], для нескольких бесконечных семейств многообразий с краем [4-7] и замкнутых многообразий [8, 9]. Оценки сложности дополнительных пространств торических узлов получены в [10].

В работе находятся точные значения и верхние оценки сложности дополнительных пространств некоторых кружевных узлов с тремя нитями.

2.    Основной результат

Кружевное зацепление (pretzel link) с тремя нитями K(p, q, r) (см. рисунок), лежащее в трехмерной сфере, определяется тройкой (p, q, r) целых ненулевых чисел. Зацепление K(p, q, r) не изменится при любой перестановке чисел p, q, r местами. Поэтому можно считать, что p < q < r . Хорошо известно, что зацепление K(p, q, r) является узлом тогда и только тогда, когда среди чисел p, q, r как минимум два нечетны.

Следующая теорема устанавливает точные значения и верхние оценки сложности дополнительных пространств некоторых кружевных узлов с тремя нитями вида K(1, q, r). Здесь под до полнительным пространством узла понимается компактное подмногообразие трехмерной сферы

S ³, получающееся вырезанием из S ³ открытой трубчатой окрестности узла. Для каждой пары натуральных чисел q , r , где q <  r , определим целое число f ( q , r ) следующим образом:

0, если q = r = 1,

2, если q = 1, r = 2,

f ⁽ q , ^r ) = -

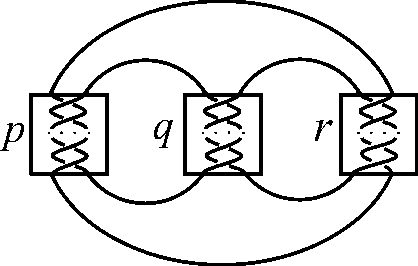
Кружевное зацепление с тремя нитями

[ r /2] + 2,       если q = 1, r >  2,

[ ( q + r )/2 ] + 3, если q >  1, r >  q .

Таркаев В.В., Фоминых Е.А.

Верхние оценки сложности дополнительных пространств некоторых кружевных узлов

Теорема. Пусть 1 <  q <  r <  15 и зацепление K (1, q , r ) является узлом. Тогда сложность c ( q , r ) дополнительного пространства узла K (1, q , r ) удовлетворяет условию c ( q , r ) <  f ( q , r ). Более того, если f ( q , r ) <  8, то c ( q , r ) = f ( q , r ).

3.    Доказательство теоремы

Опираясь на метод, описанный в доказательстве предложения 2.1.11 из [1], строим почти специальный спайн P (1, q , r ) дополнительного пространства узла K (1, q , r ). При помощи преобразований из [1, параграф 7.2] упрощаем спайн P (1, q , r ) до тех пор пока это возможно. Число истинных вершин полученного почти простого спайна Q (1, q , r ) и дает нам искомую верхнюю оценку сложности f ( q , r ) дополнительного пространства узла.

Поскольку узел K (1,1,1) является трилистником, то сложность его дополнительного пространства равна 0 (см. [10]). Если спайн Q (1, q , r ) имеет не более 8 истинных вершин, то дополнительное пространство узла K (1, q , r ) содержится в списке многообразий из [11, 12], сложность которых известна.