Верификация конечно-элементного решения трехмерных нестационарных задач упругопластического деформирования, устойчивости и закритического поведения оболочек

Несмотря на накопленный положительный опыт [1-4], границы применимости метода конечных элементов (МКЭ) для исследования геометрически и физически нелинейных задач динамики и устойчивости оболочечных конструкций еще недостаточно изучены. Серьезной проблемой, с которой приходиться сталкиваться при построении конечных элементов (КЭ), является эффект так называемого «запирания». Суть его заключается в том, что в процессе деформирования КЭ демонстрирует сильно завышенную жесткость, в результате чего невозможно получить необходимую точность решения при измельчении сетки. В ряде случаев развиваются моды нулевой энергии (неустойчивость типа «песочные часы»). В силу отмеченных недостатков численных схем представляются актуальными экспериментальные и теоретические исследования, позволяющие верифицировать существующие и разрабатываемые методы решения рассматриваемого класса задач. Ниже приводится конечно-элементная методика анализа трехмерных нелинейных задач динамики конструкций, включающих тонкостенные оболочки, и верификационные тесты для оценки ее достоверности.

2.    Определяющая система уравнений

Для описания движения деформируемой среды применяется текущая лагранжева формулировка [5,6]. Уравнение движения выводится из баланса виртуальных мощностей:

J о j 5е ij dV + J p U i 5 U i dV = J P i 5 U d у + J P i⁴ 5 U i d у ( i , j = 1, 3), ΩΩ    Γ p Γ q

где U i — компоненты вектора скорости перемещения в общей декартовой системе координат Х ; o j , s j — компоненты тензоров напряжений Коши и скоростей деформаций

(симметричной части градиента скорости перемещений); p — плотность; Pq — контактное давление; Pi — распределенная нагрузка; Q — исследуемая область; Гq — поверхность контакта; Гp — зона действия внешнего давления; 5s,, 5 Ui — вариации s,, Ui (на поверхности с заданными кинематическими граничными условиями 5Ui = 0); точка над символом означает частную производную по времени t; по повторяющимся индексам ведется суммирование. Компоненты тензора скорости деформаций определяются в метрике текущего состояния:

S j = ( U i , j + U ji )/2     ( i , j = 1,3),

U,,j = d Ui /dХу ,

t

X = X I   + [ u dt .

i            i I t = 0 J i

Компоненты тензора напряжений находятся из соотношений теории течения с изотропным упрочнением:

v (J.. — СУ • t СУ O -. 1j          ij               ij ’	(j V =- 3 K S V ,            s v =s ii /3,
•re     •       • v e        • d ′ evp ij          ij              ij ij ,	S P = 0,                 Dj o’ j = 2 G ^e ,                        (3)
• s ip = Xo‘ j ,	^j^j = 2/3 о Т ( x ) ,      X = V2/3 J ^y^P dt . 0

Здесь O j , s j , о ^v , s v — девиаторные и шаровые компоненты тензоров напряжения и скоростей деформаций; s p — скорости пластических деформаций; G, K — модули сдвига и объемного сжатия; 5 j — символы Кронекера; D J — производная Яуманна: ^D j ° j =° j -O k ^-O W , где W y = ( ^Um^{- U} jj) /2; ^о т ^— динамический предел текучести; X — параметр, тождественно равный нулю при упругом деформировании и определяемый при упругопластическом деформировании из условия прохождения мгновенной поверхности текучести через конец вектора догрузки. На контактной поверхности формулируются условия непроникания по нормали и свободного скольжения вдоль касательной к поверхности контакта:

Связь контактирующих подобластей полагается односторонней, то есть, возможен отрыв поверхностей друг от друга и повторное вступление в контакт. Система уравнений (1)–(4) дополняется начальными условиями и кинематическими граничными условиями.

3.    Метод решения

Для дискретизации определяющей системы уравнений по пространственным переменным применяется метод конечных элементов, а дискретизация по времени базируется на явной конечно-разностной схеме типа «крест» [7]. Деформируемая конструкция заменяется лагранжевой сеткой, состоящей из 8-узловых конечных элементов. В узлах сетки определяются ускорения { U } , скорости { U } и перемещения { U } в общей системе координат { X } = { X 1 X 2 X 3 } T . Конечный элемент с помощью полилинейного изопараметрического преобразования отображается на куб - 1 <5 , < 1 ( i = И) :

• X , = £ XN №1УУ . N = (1 ¹ й, / 5 k )(1 +У 5 2 )(1 + 5 3 / 5 ₃ * )/8 ,                  (5)

= 1

где X¹ . . 5 ^k — координаты узлов в базисах { X } . { 5 } ; N_k — функции формы. Компоненты скорости деформаций L j аппроксимируются в КЭ линейными функциями:

• 8 ^=8 “^j +a2L 252 +a3L j^                                       (6)

По аналогии с теорией оболочек 8 ° — значения компонент скорости деформаций в центре КЭ, далее будут называться безмоментными составляющими, а их градиенты 8 k = м': / д5 _k = const — моментными составляющими. Чтобы не завышать сдвиговую жесткость элемента. в (6) учитываются только компоненты 8 . . соответствующие изгибающим и крутящим моментам в теории оболочек типа Тимошенко [8]. Весовые коэффициенты a _k вводятся для регулирования влияния моментных составляющих скорости деформаций 8 k на численное решение (0 _k <  1. k = 1.3). На основе (6) разработано семейство конечных элементов для моделирования сложных составных конструкций.

Тип А — конечный элемент сплошной среды. Наиболее простой вариант КЭ получается при a _k <<  1. k = 1. 3. В этом случае пластические свойства материала учитываются при вычислении напряжений в центре КЭ. а связь 8 k и соответствующих им моментных составляющих скоростей напряжений полагается линейно упругой. Как показали тестовые расчеты. при a _k * 0.01 введение 8 к в численную схему позволяет подавить моды с нулевой энергией и сохранить точность методов [9, 10]. Элементы типа «А» можно применять для исследования динамики массивных тел и тонкостенных конструкций. Однако в пластинах и оболочках для достижения приемлемой точности решения сетка расчетной области должна иметь не менее четырех элементов по толщине, что многократно повышает затраты вычислительных ресурсов и оправдано только при интенсивных локальных воздействиях.

Тип В — конечный элемент оболочки. Предполагается, что в тонкостенных элементах конструкций поперечные сдвиговые и изгибные деформации малы, а смещения и углы поворота поперечного сечения произвольны. В каждом конечном элементе вводится локальный базис { x } = { x 1 x 2 x 3 } T (ось x 3 направлена по нормали к срединной поверхности), отслеживающий вращение КЭ как жесткого целого [1, 11]. При этих условиях можно считать, что ось 5 3 совпадает с x ₃ и а ₃ = 1, а 1 , а 2 <<  1 . Конечный элемент разбивается вдоль 5 ₃ на ряд подслоев. Напряжения в подслоях определяются в точках 5 1 = 5 2 = 0 из уравнений состояния, исходя из линейного распределения скорости деформаций по толщине оболочки: ё ij = ё ° +ё 3 5 3 . Для улучшения сходимости численного решения при дискретизации тонкостенных конструкций трехмерными конечными элементами вводится дополнительная гипотеза [12]: компонента тензора напряжений, направленная по нормали к срединной поверхности, не меняется по толщине оболочки. Моментные составляющие &V , ё j , описывающие изменение скорости деформаций в срединной поверхности КЭ оболочки, применяются для регуляризации численного решения (подавления мод нулевой энергии) и определяются как в КЭ сплошной среды.

Тип С — конечный элемент оболочки. Там, где в процессе деформирования возможны большие локальные формоизменения, целесообразно все коэффициенты а k в (6) положить равными единице. В направлении нормали к срединной поверхности (ось 5 3 ) конечный элемент разбивается на ряд подслоев. В отличие от предыдущего КЭ, вычисление скоростей деформаций и напряжений осуществляется не в центрах подслоев, где 5 1 = 5 2 = 0, а в квадратурных точках Гаусса. Для численного интегрирования в уравнении баланса виртуальных мощностей (1) применяются формулы, используемые в работе [3].

Мощность виртуальной работы в каждом конечном элементе выражается через матрицу масс, узловые ускорения и статически эквивалентные узловые силы. После замены интегрирования по области О суммированием по элементам получается дискретный аналог уравнений движения (1):

[ M №} = { F } . (7)

где [M] — диагональная матрица масс; {{7}, {F} — векторы, составленные из ускорений узлов КЭ-сетки и результирующих узловых сил в общей системе координат. Система обыкновенных дифференциальных уравнений (7) интегрируется по явной конечно-разностной схеме типа «крест».

Изложенная методика реализована в рамках вычислительного комплекса «Динамика-3» [13]. Далее проводится ее верификация на ряде тестовых задач.

4.    Верификационные расчеты

Задача 1 . Численно и экспериментально исследован процесс неосесимметричного выпучивания стальной цилиндрической оболочки ( h = 10^-3 м, L/h = 92, R/h = 14,5) с массивными оголовками (Рис. 1, а ) при осевом сжатии в квазистатическом режиме нагружения. Материал образца — сталь Х18Н10Т (модуль упругости Е = 210 ГПа, коэффициент Пуассона Ц = 0,3, плотность р = 7800 кг/м³), диаграмма деформирования которой приведена на рисунке 1, б .

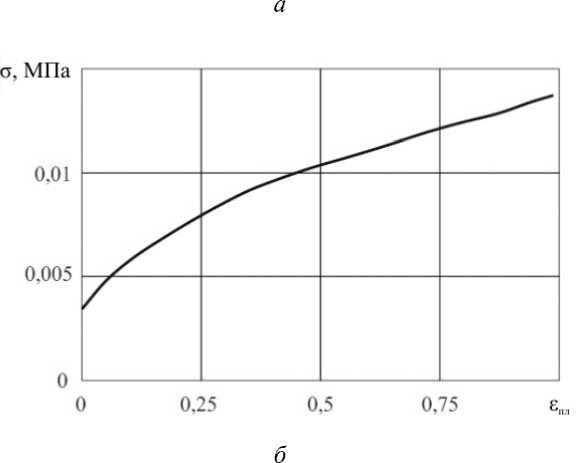
Рис. 1. Исследуемый образец ( а ) и диаграмма деформирования стали Х18Н10Т ( б )

Известно [14-16], что выпучивание металлических цилиндрических оболочек при осевом квазистатическом и динамическом сжатии происходит по осесимметричным или неосесимметричным формам. Реализация той или иной формы волнообразования зависит от скорости удара, соотношения масс ударяющего тела и оболочки, геометрии и материала оболочки. Одним из главных параметров, определяющих форму потери устойчивости оболочек средней длины, является отношение радиуса кривизны срединной поверхности к толщине оболочки R/h . Выпучивание достаточно толстых оболочек происходит с образованием складок вблизи торцов и сопровождается пластическим течением. Ниже приводятся результаты верификационных расчетов, позволяющие оценить применимость разработанных конечных элементов в этом классе задач.

В силу симметрии в расчетах рассматривалась четвертая часть оболочки, которая покрывалась сеткой из 920 конечных оболочечных элементов типа «В» или «С» (92 КЭ вдоль образующей и 10 КЭ в направлении угла поворота). Массивные оголовки моделировались конечными элементами типа «А». Результаты численного решения сравнивались с экспериментальными данными, полученными Казаковым Д.А. (НИИ механики Нижегородского университета, Н. Новгород) на установке УМЭ-10-ТМ. Процесс выпучивания происходил следующим образом. Сначала оболочка, за исключением краев, равномерно расширялась. Затем у ее торцов намечались осесимметричные складки, а прогибы в средней части фиксировались. Дальнейший рост нагрузки вызывал вначале одновременное увеличение амплитуды обеих складок. Затем рост одной из них прекращался, нагрузка достигала своего предельного значения, и наблюдалась несимметрия прогибов на растущей складке и рядом с ней. После начала трансформации осевые усилия на торце начинали уменьшаться. За складкой образовывалась вмятина, и поперечное сечение оболочки в этой области приобретало эллиптическую форму.

При исследовании устойчивости оболочки по неосесимметричной форме в расчетах задавались несовершенства в виде начальной погиби: w = A cos ( р ) sin ( 2 nx/ Z ) . Здесь A = 0,1 h , h — толщина оболочки, 0

90 ° — координата по углу поворота, 0 <  x < ( Z /2) — координата вдоль образующей, Z — длина выпучины, определяемая из осесимметричного расчета. Сжатие оболочки проводилось до величины осадки A L = 8 h .

На закритической стадии процесса выпучивания учитывалось контактное взаимодействие при замыкании гофров. В конечных элементах оболочки типа «В» при а 1 = а ₂ = 0,01 в случае больших изгибных деформаций в зоне гофров развиваются моды нулевой энергии. На рисунке 2 изображена остаточная форма трубчатого образца, полученная в эксперименте (Рис. 2, а ) и при численном решении задачи (Рис. 2, б ) с использованием конечного элемента оболочки типа «С», который обеспечивает устойчивость счета и приемлемую точность расчетов.

Как показали исследования, в процессе выпучивания оболочки имеют место упругая разгрузка и сложное нагружение. Момент начала разгрузки и ее продолжительность на срединном слое заметно отличаются от соответствующих величин на лицевых поверхностях оболочек. Сложное нагружение наиболее существенно проявляется в наружных волокнах. Анализ траекторий деформирования позволяет классифицировать их как траектории малой и средней кривизны. Большая кривизна наблюдается только на участках упругих разгрузок.

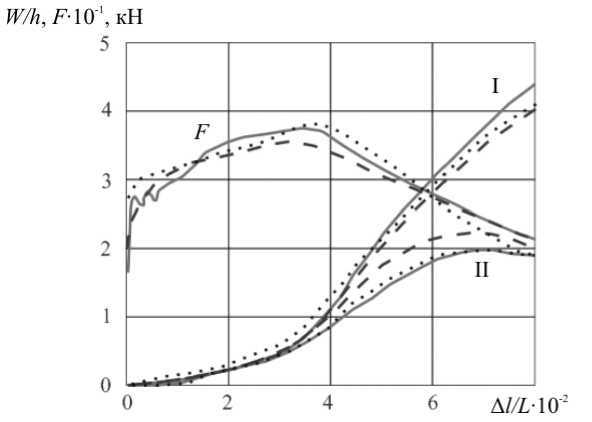
На рисунке 3 приведены графики изменения радиальных перемещений W в точках, отмеченных на рисунке 2, б цифрами I, II, а также осевых усилий F в зоне закрепления

а

б

Рис. 2. Остаточная форма образца, полученная в эксперименте ( а ), в расчете ( б )

Рис. 3. Графики изменения радиальных перемещений и осевых усилий F в зависимости от сближения торцов оболочки оболочки в зависимости от сближения торцов. Пунктирные линии отвечают экспериментальным данным, сплошные — расчету по изложенной методике с применением КЭ типа «С», штриховые — расчету с помощью пакета программ ANSYS). Расчетные и экспериментальные значения интегральных параметров процесса (прогибов и усилий) хорошо согласуются между собой. Как следует из графиков, неосесимметричная форма потери устойчивости развивается с момента, когда осесимметричная выпучина начинает превышать толщину оболочки.

Для рассмотренного выше цилиндрического образца также моделировалась задача ударного сжатия. Результаты расчета сравнивались с данными натурного эксперимента, полученными Деменко П.В. и Лаптевым П.В (НИИ механики Нижегородского университета, Н. Новгород) на установке РСГ–60 [17]. Одним из торцов образец свободно опирался на мерный стержень, по другому торцу бил ударник массой 5,4 кг с начальной скоростью V 0 = 11,93 м/с. Ударник и мерный стержень были выполнены из стали и в расчетах предполагались упругими.

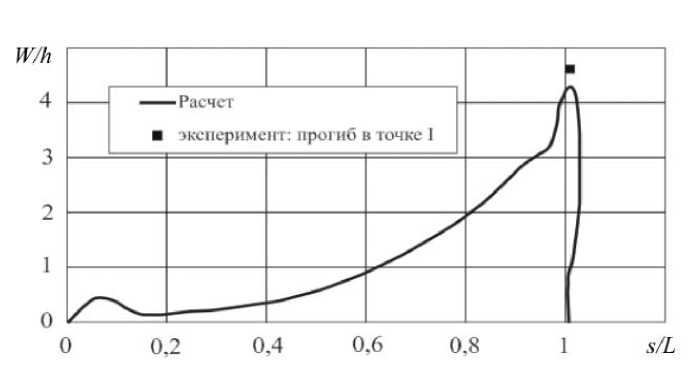
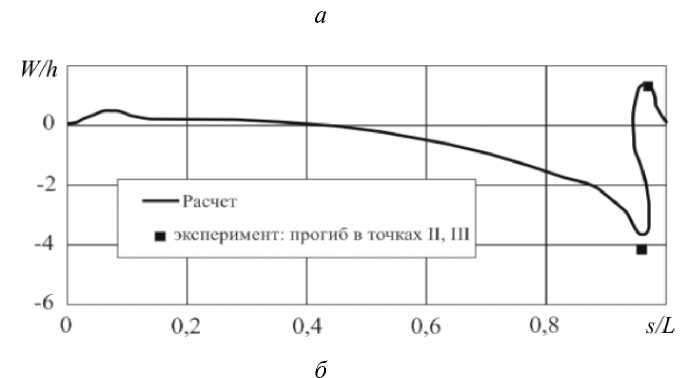
На рисунке 4, а и б представлены остаточные прогибы вдоль образующей рабочей части. Точками обозначены экспериментальные значения амплитуд выпучин. Величина осадки образца составляла: в расчете — 11,5 h , в эксперименте — 12 h . Результаты численного моделирования хорошо согласуются с экспериментальными данными, несмотря на большие формоизменения и сложный характер нагружения.

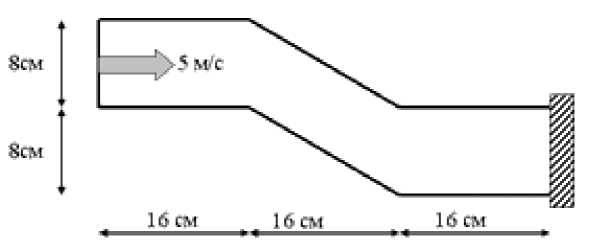
Задача 2 . Составная стальная оболочка коробчатого профиля ( h = 1,5 ⋅ 10^-3 м), изображенная на рисунке 5, деформировалась при соударении с плитой, имеющей массу 500 кг и начальную скорость 5 м/с. На правом торце конструкции задавались условия неподвижного защемления, на левом торце — условия контактного взаимодействия с плитой. Механические характеристики материала равнялись: модуль упругости — 1,99355 ГПа; коэффициент Пуассона — 0,3; плотность — 7800 кг/м³; предел текучести — 185,4 МПа; модуль линейного изотропного упрочнения — 540 МПа. При решении задачи конструкция разбивалась на 1536 конечных элементов. Результаты решения представлены на рисунках 6, 7 в виде графика зависимости сжимающей силы F от продольного смещения левого торца оболочки и формы оболочки на момент времени 16 мс.

Рис. 4. Остаточные прогибы вдоль образующей цилиндрической оболочки в сечении, проходящем через точки I ( а) и II, III ( б ) ( s – длина дуги вдоль образующей цилиндрической оболочки 0 ≤ s ≤ L )

а

б

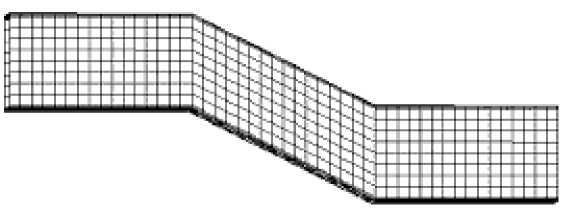
Рис. 5. Расчетная область ( а ) и конечно-элементная сетка ( б ) для задачи 2

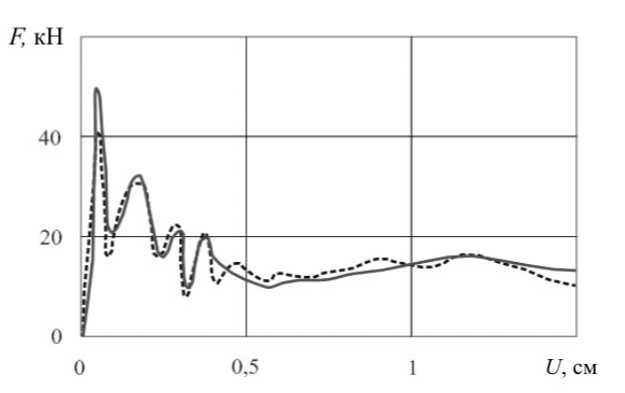
Рис. 6. Зависимость контактной силы от продольного смещения левого торца оболочки

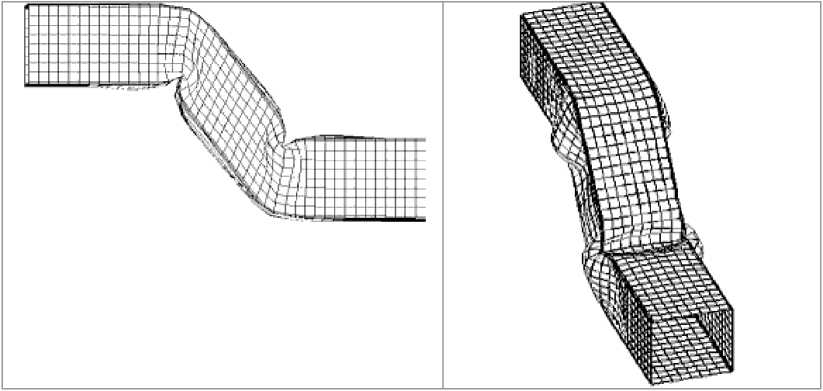
Рис. 7. Форма оболочки на момент времени 16 мс

Сплошной и пунктирной линиями на рисунке 6 отмечены результаты, полученные на основе оболочечного конечного элемента типа «С» и 4-узлового конечного элемента оболочки [18] соответственно. Расхождение этих графиков незначительно.

5.    Заключение

Результаты верификационных расчетов подтвердили эффективность разработанных моментных конечных элементов, предназначенных для математического моделирования нестационарных задач динамического деформирования тонкостенных конструкций при больших формоизменениях в условиях сложного нагружения, характерного для упругопластического выпучивания оболочек.

Работа выполнена при частичной финансовой поддержке Российского фонда фундаментальных исследований (проекты № 08-08-00560_а, 08-01-00500_а, 09-08-97034_р_Поволжье_а) и Совета по грантам Президента РФ для ведущих научных школ (грант НШ-3367.2008.8).