Верификация криптографических протоколов распределения ключей с использованием раскрашенных сетей Петри
Автор: Могилевская Надежда Сергеевна, Колчанов Сергей Сергеевич
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Физико-математические науки
Статья в выпуске: 9 (60) т.11, 2011 года.
Бесплатный доступ
Рассмотрена и оценена возможность применения раскрашенных сетей Петри для анализа криптографических протоколов распределения ключей на примере симметричного протокола Нидхема - Шрёдера.
Верификация протокола, формальный анализ, распределение ключей, протокол нидхема - шрёдера, раскрашенные сети петри
Короткий адрес: https://sciup.org/14249709
IDR: 14249709 | УДК: 004.414.023
Текст научной статьи Верификация криптографических протоколов распределения ключей с использованием раскрашенных сетей Петри
Введение. Одной из наиболее важных задач, которые необходимо решать при организации защиты информационной системы с помощью криптографических алгоритмов, является задача управления ключами. Очевидно, что как бы ни была сложна и разумно устроена криптосистема, некорректное обращение с ключами может значительно понизить уровень её защищённости. Под управлением ключами принято понимать информационный процесс, включающий в себя четыре основных элемента: генерацию ключей, накопление ключей, распределение ключей, процедуру их ввода и синхронизации [1, 2]. Наиболее распространённым решением задачи распределения ключей является использование специализированных криптографических протоколов.
Фактически криптографический протокол — это распределённый алгоритм, определяющий последовательность шагов, точно специфицирующих действия, которые требуются от участников для решения некоторой криптографической задачи, например, обеспечение целостности, секретности, аутентичности информации [2, 3, 4]. При анализе качества протокола необходимо обратить внимание не только на достижение желаемого результата всеми участниками протокола, но и на недопустимость проведения атак на протокол злоумышленниками. Отметим, что при анализе протокола используемые в нём криптографические алгоритмы и примитивы считаются надёжными, а анализу подвергаются сообщения, которыми обмениваются участники протокола, а именно их содержимое и порядок следования. Формальный анализ и выявление недостатков криптографических протоколов на деле оказывается весьма затруднительным. Известны факты, когда протоколы даже с небольшим количеством сообщений долгое время скрывали свои уязвимости [2, 4, 5].
Существует ряд математических аппаратов, используемых для решения задачи формального анализа протокола, например, модальные логики, конечные автоматы, спецификационные языки [2, 4, 6]. Эти подходы достаточно новые, каждый из них имеет как достоинства, так и недостатки. В обзорных работах по формальным методам анализа протоколов часто упоминается возможность верификации протоколов на основе моделирования сетями Петри, однако, исследований, посвящённых именно этому вопросу, достаточно мало, например [4, 6, 7, 8]. Цель работы. Рассмотреть и оценить возможность применения сетей Петри к верификации криптографических протоколов распределения ключей. Для достижения цели в работе с помощью раскрашенных сетей Петри для ряда криптографических протоколов построены модели. По итогам исследования моделей сделаны выводы о возможности верификации криптографических протоколов распределения ключей с использованием раскрашенных сетей Петри. В работе исследован ряд протоколов, однако наиболее подробно рассмотрена модель выработки сеансового ключа симметричного протокола Нидхема — Шрёдера.
Протокол Нидхема — Шредера. Этот протокол хорошо изучен. Он получил широкую известность, так как долгое время скрывал свою уязвимость в обеспечении безопасности [2, 5]. Целью данного протокола является выработка общего сеансового ключа АдвДля участников протокола А и Вс использованием доверенного посредника 8. Говоря о доверенном посреднике для выработки ключей, мы считаем, что участники А и Буже имеют долговременные ключи для общения с ним, а кроме этого, доверяют 8 вырабатывать ключ для связи между участниками. Запишем протокол в виде схемы обмена сообщениями.
1. А^8:А, В, NA. 2. S^AANa,B,KabAKab,A>Kbs>k3. а^вакдв,а>к.4. B^AANAk .
I и Кду
5. A^BANb-1>k
Здесь А, В, 8 — участники протокола; NA, NB — уникальные числовые вставки (нонсы), используемые только в одном сеансе связи; KAS, Kbs, Кав — ключи для обмена сообщениями между участниками А и 8, В и 8, А и В, соответственно; запись типа {^означает шифрограмму от X на ключе К; запись типа >4 —> S: Xi, Х2 означает, что участник А отправляет 8 сообщения Xi, Х2. Считается, что до начала протокола у участников есть договорённость об используемых криптографических алгоритмах и о порядке следования элементов в сообщениях.
Прокомментируем шаги протокола. На первом шаге пользователь А сообщает доверенному серверу 8, что он намерен получить ключ для переписки с В. Во втором сообщении 5 генерирует ключ КАВ и посылает его А, в сообщении содержится также цифровая вставка МА, по которой А узнаёт, что он получил сообщение сервера на свой запрос. На следующем шаге А отправляет Б ключ КАВ, зашифрованный на ключе KBs. Участник Б доверяет этому посланию, так как оно зашифровано на ключе доверенного сервера 8, а имя А, указанное в этом сообщении, говорит В, что ключ КАВ предназначен для общения с А. Участник В на 4-м шаге должен проверить, что отправитель сообщения {^,>4}^ действительно является А и этот участник намерен установить защищённый обмен сообщениями. Для этого он отправляет А свой ноне в зашифрованном виде. В последнем сообщении, чтобы убедить партнёра В в своей дееспособности, инициатор переговоров шифрует простое выражение, зависящее от NB, и отправляет его А. Если все шаги протокола выполнены, то участники считают, что у них есть надёжный сеансовый ключ КАВ.
Процедура с использованием нонсов NA, NBv\ NB- 1 служит для подтверждения участниками факта новизны, или, как принято говорить, свежести сеансового ключа КАВ, т. е. для подтверждения того, что указанный ключ был впервые использован в данном сеансе связи и не использовался ранее для связи этих двух участников. Основным недостатком рассмотренного протокола является то, что В не уверен в свежести ключа КАВ, полученного на третьем шаге. Таким образом, злоумышленник М может записать сообщения прошлых сеансов протокола и впоследствии использовать их для атаки на протокол [5].
Опишем схему протокола Нидхема — Шрёдера с атакующим злоумышленником.
1. A^S\A,B,Na.2. 8 ^A\{Na,B,KabAKab,A}k }, .
А' * AD AD ^BS AS
3. м^в\^кАВ,д>к 4. B^AANbX„.5. M^AANb>k, 6. a^banb-i}^ 7. M ^ВАМЛК, .
L В J К AR
На третьем шаге М отправляет старое сообщение от имени А, на четвёртом перехватывает сообщение и заменяет его на пятом шаге. Таким образом, М подменяет сообщения, адресованные В, а В верит в то, что он совместно с А в реальном времени вырабатывает новый сессионный ключ КАВ.
Раскрашенные сети Петри. Сети Петри — это весьма востребованный математический аппарат для моделирования динамических дискретных систем. Сеть Петри может быть задана как алгебраически, так и графически. С точки зрения алгебры, сеть Петри задаётся кортежем следующего вида С = (Р, Т, I, О, ц), где Р, Т— конечные множества позиций (состояний сети) и переходов (событий сети), I, О — множества входных и выходных функций, ц — вектор натуральных чисел, определяющий маркировку сети. Графически сеть Петри представляет собой двудольный ориентированный граф, в котором позициям соответствуют вершины, изображаемые кружками, а переходам — вершины, изображаемые чёрточками или прямоугольниками; функциям I соответствуют дуги, направленные от позиций к переходам, а функциям О —дуги, направленные от переходов к позициям. Дугами могут соединяться только вершины различных типов. Для описания динамики процессов, реализуемых в сети Петри, дополнительно вводится понятие фишки. Размещение фишек по позициям сети называется маркировкой ц. Перемещения фишек по сети представляют собой совокупность срабатываний переходов и отображают смену дискретных состояний моделируемой системы. Срабатывание перехода возможно, если имеется соответствующее переходу событие (т. н. предусловие). Выполнение события представляется фишкой в позиции, соответствующей этому условию. При запуске (срабатывании) перехода из входных позиций (предусловий) фишки удаляются, а в выходных позициях (постусловиях) — появляются. В раскрашенных сетях фишки являются элементами некоторого абстрактного типа данных, традиционно называемого цветом. Подробное описание сетей Петри хорошо представлено, например, в [9].
Идея построения моделей криптографических протоколов на основе раскрашенной сети Петри. Для построения сети Петри, отражающей работу протокола, выделим два типа объектов в моделируемом протоколе, а именно состояния и события. Под состояниями будем понимать такие сущности, как ключ, ноне, сообщение, т. е. объекты, состояние которых можно охарактеризовать одним из двух значений, например, 1 — состояние реализуется, 0 — нет. Под событиями в модели будем понимать нечто, происходящее практически мгновенно, например, отправка или получение, зашифровывание или расшифровывание сообщения. Выделенные состояния используем в качестве позиций сети, а события в модели будут представлены переходами.
Каждому участнику протокола соответствует часть построенной сети, содержащая позиции и переходы, связанные с ключами этого участника и сообщениями, которые он отправляет другим участникам. Части сети, соответствующие различным участникам протокола, между собой не пересекаются. Отметим также, что одной сущности в протоколе может соответствовать несколько позиций в сети. Как правило, эти позиции относятся к разным участникам протокола. Например, секретный ключ двух участников протокола представлен позицией у каждого из уча- стников, а также, в зависимости от протокола, он может быть представлен дополнительно в канале связи.
Как и во всех моделях, построенных на основе сетей Петри, наличие и значение сущности в позиции определяется фишкой, а движение фишек по сети является предметом анализа сети. Для движения фишек необходимо срабатывание переходов, которое, как и наступление событий в реальной системе, определяет ход работы протокола.
В сеть может быть добавлена позиция, обозначающая успешное завершение работы протокола. Фишка в эту позицию попадает, например, если легальные участники протокола получают общий сессионный ключ. Тогда, анализируя свойство достижимости сети, при которой в этой позиции окажется нужная фишка, можно определить, приведёт ли протокол к заданной цели, а также выяснить, наступление каких событий может этому помешать.
Для проведения анализа модели криптографического протокола необходимо либо построить дерево достижимости; либо многократно запускать работу сети с различным порядком срабатывания переходов, перебирая все возможные варианты, и при этом отслеживать основ-
-
▼ Declarations
-
► Standard priorities
-
▼ Standard declarations
-
► colset UNIT
-
▼ colset INT = int;
-
► colset BOOL
-
► colset STRING
-
▼ User declarations
-
▼ colset PS=string with "a".."z" and 3..3;
-
▼ var Kab: PS;
-
▼ varNb_Kab, Nbl_Kab: STRING;
▼fun F(a)=aA"-l";
-
▼ var i: INT;
-
▼ var М2: STRING;
-
▼ var Kas, Kbs, Kab_Kbs: STRING;
-
▼ var Na, Nb, Nbl, Nb2: STRING;
Рис. 1. Описание переменных в терминах языка программирования CRN ML
ные характеристики сети; либо использовать матричную теорию сетей Петри для отслеживания возможных маркировок сети [9]. Далее в работе будем использовать многократный запуск сети с помощью автоматизированных инструментов.
Программный комплекс CRN Tools. Чем больше позиций и переходов содержит сеть Петри, тем сложнее её корректное построение и анализ. Для анализа моделей криптографических протоколов распределения ключей в работе использован программный комплекс CRN Tools [10], разрабатываемый группой AIS Эйндховен-ского университета технологий (Нидерланды) (Eindhoven University of Technology, The Netherlands). Раскрашенные сети Петри моделирующей системы CRN Tools представляют собой комбинацию графа сети Петри и языка программирования CRN ML, используемого для описания
типов элементов сети. CRN Tools обладает средствами для наглядного и удобного построения и исполнения сетей Петри, обеспечивает проверку структуры конструируемых сетей, быстрое их исполнение, проведение полного или частичного анализа пространственных состояний, автоматическую проверку живости и связности. Важными характеристиками CRN Tools являются его свободное распространение, мультиплатформенность, качественная техническая поддержка и доступность документации справочного характера.
Модель протокола Нидхема — Шредера на основе раскрашенной сети Петри. Опишем разработанную модель подробнее. На рисунке 1 с использование языка CRN ML представлена часть описания модели, построенной в системе CRN Tools. Специальный тип данных PS был задан для описания ключей. Далее в переменных этого типа методом гап() языка CRN ML будут генерироваться случайные значения — аналоги случайных ключей. Строки описания, начинающиеся со служебного слова var, задают переменные. Описание назначения, начального значения, а также указание участников, к которым относятся эти переменные, представлены в таблице 1.
Описание переходов, используемых в построенной модели, находится в таблице 2. В левом столбце указаны названия переходов, а в правом — описания связанных с каждым из них событий. Отметим, что, так как средствами CRN ML нельзя описать алгоритм шифрования, то для имитации шифрования в работе использована конкатенация строк сообщения и ключа.
Таблица 1
Описание фишек-переменных построенной модели
|
Переменная |
Нач. значение |
Назначение |
Переменная |
Нач. значение |
Назначение |
|
Участник А |
Участник В |
||||
|
Na |
«1» |
НонсЛ |
Kbs |
«kbs» |
Общий ключ Ви S |
|
Kas |
«kas» |
Общий ключ А и S |
Кав |
— |
Сеансовый ключ |
|
КаВ |
— |
Сеансовый ключ |
Ng |
«2» |
Ноне В |
|
Nb |
— |
Ноне В |
Na |
— |
Ноне, полученный от А, после обратной операции |
|
Nbi |
— |
Обработанный ноне В |
Na |
— |
Ноне, полученный от А |
|
Участник В |
Дополнительные переменные |
||||
|
Kbs |
«kbs» |
Общий ключ 8 и S |
Л6 |
Канал связи между А и S |
|
|
Kas |
«kas» |
Общий ключ А и S |
Kab_Kbs, Nb_Kab, Nbi_Kab |
Канал связи между А и В. Имя переменной совпадает с именем фишки, для которой она предназначена. |
|
|
Кав |
— |
Сеансовый ключ |
Final! |
Конечная позиция. Содержит true в случае успешного выполнения протокола, иначе — false. |
|
|
Na |
— |
Ноне 4 |
|||
Таблица 2
Описание переходов построенной модели
|
Название перехода |
Описание действия |
|
Т1 |
При появлении фишки-нонса Na у участника А генерирует новый сеансовый ключ ^дкак случайное значение типа РВи сохраняет ноне для дальнейшего использования. |
|
Т2 |
Используя Kbs, шифрует сеансовый ключ Кав- |
|
ТЗ |
Собирает в одно сообщение Na, ^Кав }^ , Кав, шифрует это сообщение ключом Kas и отправляет сообщение в канал связи. |
|
Т4 |
Отправляет Na к участнику S(инициирует работу всего протокола). |
|
Т5 |
Расшифровывает сообщение, извлекает из него Na, Кав, сеансовый ключ, зашифрованный ключом участника В, Kab_Kbs. Сохраняет Кавв позиции Кав, относящейся кА Kab_Kbs отправляет в канал связи с В. |
|
Тб |
Срабатывает при получении от Внонса, зашифрованного сеансовым ключом. Используя сеансовый ключ из позиции А, расшифровывает ноне участника Ви сохраняет его для дальнейшего использования. |
|
Т7 |
Получает обработанный ноне Л/а участника Bv сеансовый ключ Кав. Шифрует Na ключом Кав и передаёт в канал связи. |
|
Т8 |
Принимает переменную-нонс Nb, сохраняет результат вычисления функции F(cm. рис. 1) от значения нонса. |
|
T9 |
Срабатывает при появлении в канале связи сообщения от А Расшифровывает сообщение с помощью общего ключа Ви Ви сохраняет сеансовый ключ. |
|
Т10 |
Выполняет действия, обратные действиям перехода Т8 с входящей фишкой и сохраняет результат. |
|
Т11 |
Финальный переход. Получает исходный ноне участника В, и ноне, полученный после обработки А. Отправляет в позицию Final! фишку true, если нонсы равны, иначе отправляет фишку false. |
|
Т12 |
Расшифровывает сообщение от А сеансовым ключом Кави сохраняет результат. |
|
ИЗ |
Шифрует ноне участника В сеансовым ключом и отправляет его в канал связи. |
Граф модели Петри рассматриваемого протокола, построенной в системе CRN Tools, представлен на рисунке 2. Из теории известно, что граф сети Петри задаёт алгебраическую структуру сети однозначно и наоборот, поэтому выписывать алгебраическую структуру в явном
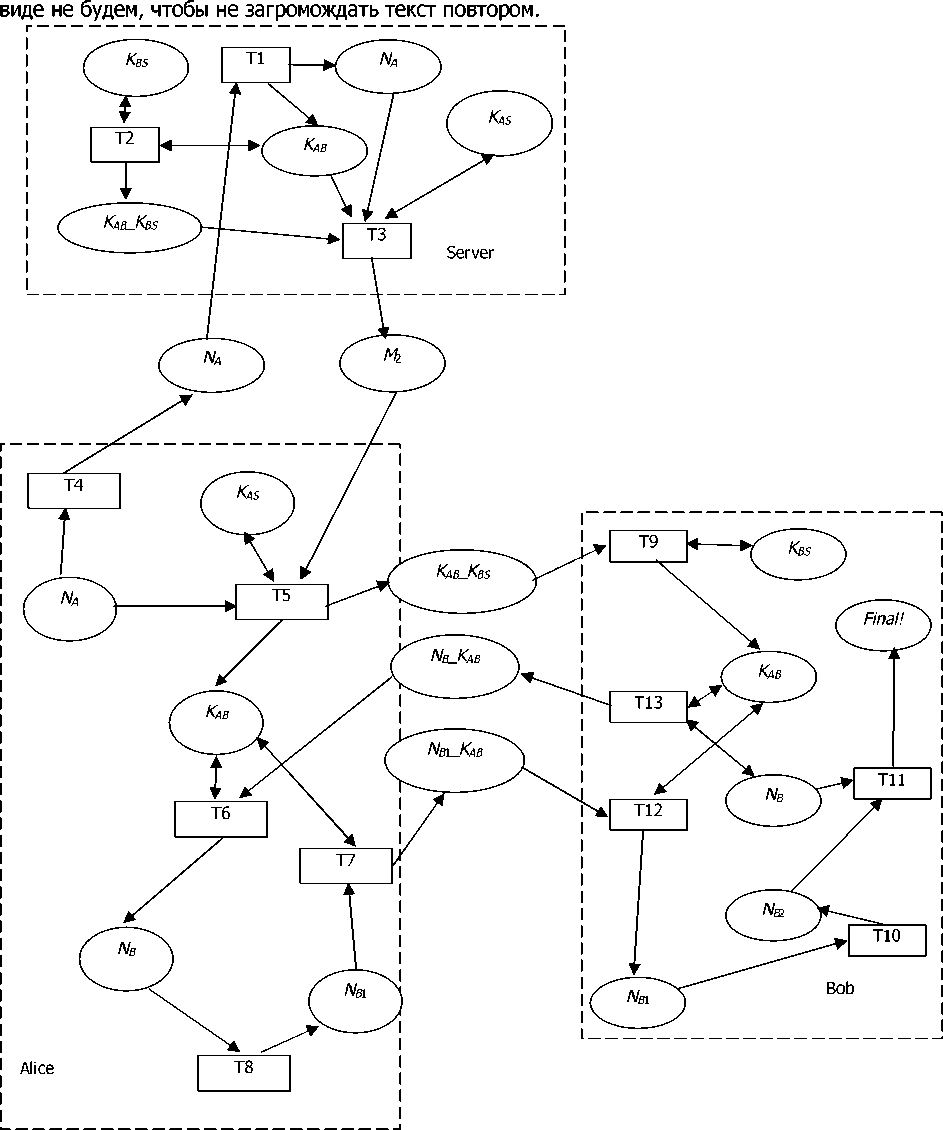
Рис. 2. Сеть Петри, моделирующая работу протокола Нидхема — Шрёдера
На графе пунктиром выделены части сети, относящиеся к различным участникам. Позиции, не вошедшие ни в какое выделение, относятся к каналу связи. Очевидно, что для построения модели злоумышленника, действующего в канале связи, необходимо «привязывать» его работу именно к этим позициям.
Результаты анализа работы модели протокола Нидхема — Шредера. Желаемая конечная разметка с фишкой true в позиции Final! и одинаковыми фишками — сеансовыми ключами в позициях КАв n Алисы и Боба достигается при всех возможных вариантах последовательности срабатывания переходов, следовательно, цели протокола по результатам его исполнения достигаются. Сеть не имеет тупиковых разметок и неустойчивых переходов, следовательно, в реальной информационной системе протокол будет работать устойчиво. Во время выполнения протокола не возникает зацикливаний, количество фишек ни в одной из позиций не разрастается, следовательно, в технической реализации протокола могут быть наложены ограничения на объём памяти. Однако известная слабость протокола, связанная с возможностью использования старых сеансовых ключей, в данной модели никак себя не обнаруживает.
Результаты исследования моделей для других протоколов. В ходе данного исследования кроме модели протокола Нидхема — Шрёдера были построены модели протоколов Диффи — Хеллмана, Station-to-station и широкоротой лягушки. Модель протоколов Диффи — Хеллмана и Station-to-station выработки общего ключа, как и модель протокола Нидхема — Шрёдера, не показывает возможность реализации атаки типа «человек посередине». Однако, зная о возможности этой атаки, авторы сумели построить модели этих протоколов с учётом работы злоумышленника в сети. Полученные модели подтвердили возможность реализации такой атаки. Модель протокола широкоротой лягушки показала слабость протокола, связанную с отсутствием подтверждения получения ключа вторым участником протокола. Таким образом, в результате случайного или преднамеренного искажения ключа в канале связи между участником А и доверенным сервером 5 или между 5 и В возможна ситуация, когда участники А и В пользуются различными ключами и, как следствие, не могут читать сообщения друг друга.
Выводы по проведённым модельным экспериментам. Подведём итоги анализа моделей криптографических протоколов распространения ключей на основе сетей Петри.
К несомненным достоинствам использования сетей Петри относится их широкая распространённость. В связи с этим существует много работ, посвящённых развитию и анализу сетей, а также существуют легко доступные качественные программные средства, часто свободно распространяемые, позволяющие анализировать сети Петри в автоматическом режиме, например использованный в работе комплекс CRN Tools.
Анализ модели протокола, построенной в виде сети Петри, позволяет сделать ряд выводов, касающихся технической стороны реализации протокола. Так, достижимость финальной разметки показывает возможность достижения сетью желаемых результатов. Анализ безопасности и консервативности сети позволяет сделать вывод о возможности введения ограничений на технические средства в реальной информационной системе, например на ёмкость памяти. Рассмотрение уровня активности переходов сети позволяет выявить избыточные переходы, ситуацию взаимной блокировки в моделируемой системе, а также переходы, срабатывание которых ничем не ограничено, а, следовательно, они могут отправлять необоснованно большое количество данных в канал связи.
Сети Петри позволяют оценить возможности мошенничества легальных пользователей или работы злоумышленников в случае, когда модель криптографического протокола соединяется с моделью злоумышленника. Эта проблема исследуется в [7].
Часто исследователи к достоинствам моделей на основе сетей Петри относят их наглядность. Однако, на наш взгляд, это весьма спорное мнение, и чем больше элементов в протоколе, тем более объёмным и запутанным становится граф сети Петри.
Укажем недостатки верификации протоколов с помощью сетей. Так, при использовании сетей Петри строго не определён процесс специфицирования, то есть процесс построения графа сети по протоколу. Фактически сеть, моделирующую работу протокола и действующего в ней злоумышленника, исследователю протокола необходимо создать вручную, что не позволяет полностью автоматизировать процесс и чревато ошибками реализации. Однако отметим, что это замечание справедливо для всех известных авторам методов математического исследования криптографических протоколов.
Модель криптографического протокола, построенная с помощью сети Петри, сама по себе малоинформативна с точки зрения возможностей злоумышленников, а также знаний и доверий легальных участников протокола и не обнаруживает многих уязвимостей. Таким образом, формальный анализ уязвимостей невозможен, допустимо лишь проверить на модели степень опасности уязвимости, найденной другим способом.
Заключение. В работе построены модели симметричных протоколов распределения ключей Нидхема — Шрёдера, Диффи — Хеллмана и широкоротой лягушки.
Результаты работы показали, что сети Петри не могут быть основным или единственным инструментом для проведения верификации криптографических протоколов. Они могут быть использованы лишь во вспомогательных целях. Во-первых, сети Петри можно применять для доказательства возможных атак и их демонстрации, во-вторых, для определения достижимости конечной маркировки, т. е. подтверждения, достигает ли протокол своей цели, в-третьих, для оценки возможности введения ограничений на технические средства в реальной информационной системе, где используется исследуемый протокол. И, наконец, для исследования возможности возникновения в протоколе «тупиков», т. е. ситуаций, когда действия участников недостаточно полно специфицированы.
Однако представляется целесообразным построение сетями Петри моделей узкого класса криптографических протоколов, в которых для подтверждения свежести ключа кроме нонсов используются и метки времени. Такая техника используется, например, в протоколах Керберос, DASS, Ньюмана — Стабблбайна [2]. Метка времени может указывать либо на время действия сеансового ключа, либо на время жизни нонса. В таком случае для моделирования нужно использовать временные сети Петри, которые отличаются от простых сетей Петри учётом времени, что позволяет моделировать не только последовательность событий, но и их привязку ко времени. Это осуществляется приданием переходам веса — продолжительности (задержки) срабатывания. Модели протоколов распределения ключей, построенные таким образом, позволят оценить безопасный диапазон времени действия ключей и нонсов.
Список литературы Верификация криптографических протоколов распределения ключей с использованием раскрашенных сетей Петри
- Основы криптографии/А. П. Алфёров [и др.]. -Москва: Гелиос АРВ, 2005. -480 с.
- Denning, D. E. Time stamps in Key Distribution Protocols/D. E. Denning, M. Smid//Communications of the ACM. -1981. -V. 24. -P. 533-536.
- Котенко, И. В. Верификация протоколов безопасности на основе комбинированного использования существующих методов и средств/И. В. Котенко, С. А. Резник, А. В. Шоров//Труды СПИИРАН. -2009. -Вып. 8. -С. 292-310.
- Могилевская, Н. С. Сравнение возможностей сетей Петри и BAN-логики в анализе криптографических протоколов проверки подлинности и обмена ключами/Н. С. Могилевская, С. С. Колчанов//Системный анализ, управление и обработка информации. -Ростов-на-Дону: Изд. центр ДГТУ, 2011. С. 98-101.
- Смарт, Н. Криптография/Н. Смарт. -Москва: Техносфера, 2006. -528 с.
- Lin, H. Algorithms for Cryptographic Protocol Verification in Presence of Algebraic Properties: diss. for the degree of Doctor of Philosophy (Mathematics). -Clarkson University, 2009.
- Nieh, B. Modeling and analyzing cryptographic protocols using Petri nets/B. Nieh, S. Tavares//Auscrypt'92, 1992.
- Salah, A. Protocol verification and analysis using colored Petri nets/A. Salah, M. Khaled. -Cairo University, 2003. -P. 3-7.
- Котов, В. Е. Сети Петри/В. Е. Котов. -Москва: Наука, 1984. -160 с.
- CPN Tools Homepage. Documentation. Electronic resource. Access mode: http://cpntools.org/documentation/start/(date of access: 11.04.2011).


