Верификация пакетов для расчета течений жидкости в канале при действии внешнего магнитного поля

Физические процессы магнитной гидродинамики присутствуют во многих промышленных отраслях, например, в атомной электроэнергетике, металлургии, в измерительной технике и другом. Эти процессы описываются дифференциальными уравнениями в частных производных, аналитическое решение которых

найти невозможно без значительных допущений. Современная тенденция в области магнитогидродинмики — это использование численных моделей [1–4]. Основная цель этой статьи состоит в том, чтобы, во-первых, представить научному и инженерному сообществу результаты верификации и оценки производительности разработанного авторами решателя, предназначенного для задач течения жидкости в канале при воздействии магнитного поля, а во-вторых, помочь исследователям в выборе адекватных вычислительных средств.

Задача течения жидкости при воздействии магнитного поля изучается для понимания процессов, происходящих в термоядерных реакторах [5], измерения силы Лоренца [6] и скорости потока в канале [7], кристаллизации металла [8] и во множестве других приложений. Магнитное поле может вести себя подобно твердому препятствию [9] или, наоборот, придать потоку жидкости ламинарный характер [10]. Эти явления часто рассматривают как модификации задачи Гартмана, как, например, в работах [11, 12], где магнитное поле считается постоянным во времени. Для ряда технических приложений выводы, сделанные в этих работах, не приемлемы, например, для случаев переменного и бегущего магнитных полей, описанных, соответственно, в [8] и [13]. Одна из задач связана с проектированием рабочей конструкции индукционного насоса для режимов работы при расходе 3 м3/с и давлении выше 8 бар [14]. При таких условиях в рабочем канале возникают сильные турбулентные течения, обратные потоки и сильные механические воздействия на его стенки, что делает работу насоса невозможной. При этом линейная теория устойчивости не позволяет с достаточной точностью предсказывать переход от ламинарного режима к турбулентному, а проведение эксперимента осложняется агрессивностью металла, его непрозрачностью и высокими температурами. Поэтому возникает необходимость в разработке численной модели, которая способна с достаточной точностью прогнозировать поведение подобных систем.

Такие задачи решались с использованием коммерческих программ ANSYS [15], Comsol Multiphysics [16]. В работах [15, 17] с помощью ANSYS CFX 18.2 исследовалось поведение потока жидкости в устройствах сложной формы с тонкими стенками, обладающими различной электропроводностью, для чисел Гартмана выше 1000. Пакет Comsol Multiphysics успешно применен при расчетах термоядерного синтеза в [16] и работы индукционных насосов в [18, 19]. Некоторые из авторов названных публикаций параллельно развивали свои коды применительно к задачам магнитной гидродинамики [10, 20, 21]. Большой вклад в развитие вычислительной магнитной гидродинамики внесла работа [22]. Ее авторы разработали собственный код для расчетов течения жидкости при воздействии постоянного магнитного поля. Эти же авторы в работе [10] провели анализ корректности использования различных моделей турбулентности для различных типов задач магнитной гидродинамики. Интерес для задач магнитной гидродинамики представляет работа [13], где на основе HERACLES кода [23] исследовались потоки жидкости в неидеализированных магнитных системах. В [24] авторы предлагают ряд подходов к учету конечности и вихревой природы магнитного поля на основе граничных условий, что позволяет снизить вычислительные ресурсы. Прямое моделирование провели авторы работ [20, 21, 25], в которых рассмотрели влияние магнитных эффектов на поведение потока жидкости.

Преимуществом коммерческих численных пакетов является возможность реализации широкого спектра задач, но в то же время это достоинство является недостатком при решении задач, требующих особенных настроек, однако эти задачи можно решать с помощью программ с открытым кодом, как в [26]. Программы с открытым кодом для численного моделирования, как правило, создаются под конкретную задачу и тестируются на ней, что вызывает сложности использования этого инструмента для других случаев и требует дополнительной валидации.

В данной работе предлагается код для расчета течений жидкости в каналах, находящихся под воздействием магнитного поля, и проводится его верификация. Рассматриваемый код позволяет объединить преимущества метода конечных элементов в задачах электродинамики и метода конечных объемов в задачах течения жидкостей посредством программ с открытым кодом. Одним из известных способов верификации моделей является упрощение исходной постановки до такой степени, для которой существует аналитическое решение, как сделано в работе [27]. Это позволяет масштабировать результаты верификации для большого спектра задач и принимать в качестве эталона аналитические выражения, полученные в работах [28, 29]. Поэтому в настоящей работе на первом этапе сравниваются численные и аналитические решения для двумерного случая. Сопоставляется эффективность применения встроенных решателей OpenFOAM и решателя, предлагаемого авторами в двухмерном и трехмерном случаях, оценивается производительность этих решателей и коммерческих пакетов Comsol и ANSYS.

2.    Описание математической модели

Явления магнитной гидродинамики в несжимаемой жидкости можно описать уравнениями сохранения момента и массы:

— + ( V- U ) U -W² U = -v p + J ^ B , d t   ^V     ’                  p p

∇⋅U=0, где t — текущее время процесса, U — вектор скорости потока, ∇ — оператор набла, ν — кинематическая вязкость, p — давление; ρ — плотность, J и B — векторы плотности тока и магнитной индукции соответственно. Плотность тока в уравнении (1) можно определить из закона Ома в дифференциальной форме:

J=σ⋅(-∇ϕ+U×B).(2)

Если в (2) пренебречь токами смещения и использовать факт неразрывности линий тока ∇ ⋅ J = 0 , то получим уравнение:

∇2ϕ = ∇⋅(U×B),(3)

а вектор магнитной индукции рассчитаем согласно закону об электромагнитной индукции:

∂B = 1 ∇2B+∇×(U×B).(4)

∂ t   µ ₀ σ

В уравнениях (2)–(4) приняты обозначения: ϕ — скалярный электрический потенциал; σ — электропроводность; µ — магнитная проницаемость.

Уравнение (4) можно переписать в виде:

∆ A -µσ∇ϕ+µσ ( U ×∇× A ) = -µ J ,                          (5)

где использовано выражение для векторного магнитного потенциала A :

B =∇× A .

Представленные уравнения должны быть дополнены граничными условиями, учитывающими свойства стенок (поверхностей Γ ) канала, по которому перемещается поток жидкости:

– для изолированных стенок

B ( Γ ) = B либо J ⋅ n = 0 ;

– для сверхпроводящих стенок

^{∂ B} = 0 либо ϕ (γ)=0. ∂ n

Решение уравнений (1) и (4) можно осуществить с помощью программы с открытым кодом OpenFOAM посредством встроенного решателя «mhdFoam» [30]. Недостатком такого подхода является использование для расчета магнитного поля метода конечных объемов. В реальных задачах магнитные системы часто имеют сложную конфигурацию, которую необходимо учитывать. При этом процесс численной реализации таких задач методом конечных элементов является более устойчивым по сравнению с методом конечных объемов. Кроме того, возникают проблемы со сходимостью решения вследствие негладкости функционала магнитной индукции (4) в зонах больших токов или изменения магнитной проницаемости.

В настоящей работе рассматриваются возможности применения модернизированного решателя программы OpenFOAM для расчета гидродинамического поля U согласно (1) с помощью метода конечных объемов и проведения расчетов распределения магнитной индукции, плотности тока и силы Лоренца в открытом пакете Elmer методом конечных элементов. Обмен данными между этими программами будет осуществляться по технологии MPI (Message Passing Interface) с использованием библиотеки EOF-library [31]. Такая процедура позволяет запускать программы параллельно и производить между ними быстрый обмен информацией. Эти особенности являются важными для задач со сложной геометрией расчетных областей и неравномерным распределением искомых полей в пространстве и во времени.

На рисунке 1 приведена блок-схема модернизированного решателя. На первом шаге библиотека EOF устанавливает взаимосвязь между сетками из OpenFOAM и Elmer. Затем производится расчет магнитного поля в пакете Elmer, найденные значения усилий, магнитной индукции и тока снова с помощью библиотеки EOF передаются в уравнение гидродинамики (1). После передачи данных выполняется расчет поля скоростей в пакете OpenFOAM. Здесь на каждом временном шаге осуществляется корректировка решения по давлению

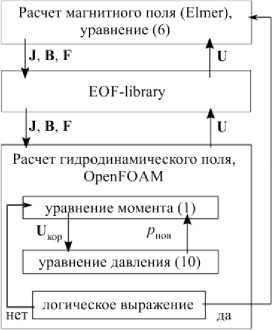
Рис. 1. Блок-схема предлагаемого решателя

V2 p = f (U, и проверяется логическое выражение. Если оно является истиной, магнитная задача пересчитывается с текущими значениями скоростей. Логическое выражение можно задавать любым, например, при определенном значении относительной разности значений максимальной скорости с предыдущего и текущего временных шагов оно может считаться истинным. В данном исследовании пересчет магнитной задачи производится на каждом временном шаге решателя.

Стоит отметить, что на данном этапе разработки решателя реализованы возможности использования усредненных и мгновенных значений усилий, а именно: магнитную задачу можно решать не только на каждом временном шаге, но и на каждой N -й итерации решателя в заданном пользователем временном интервале или в соответствии с определенным логическим выражением.

3.    Результаты

Решается задача течения жидкости в прямоугольном канале длиной L = 20 м и поперечным сечением шириной 2 a и высотой 2 b (Рис. 2). На входе в канал зададим скорость, для повышения сходимости процесса счета и снижения времени вычислений представим ее в виде параболической функции. Таким способом, по Гартману, быстрее достигается развитое распределение скорости потока. Магнитное поле проходит через две горизонтальных стенки канала, равномерно распределяется в пространстве перпендикулярно потоку жидкости и со временем не изменяется.

Рассмотрим канал квадратного сечения ( a = Ь ). В численных расчетах воспользуемся неравномерной ортогональной сеткой с числом элементов nx х ny х nz = 100 х 60 х 60. Слои сетки имеют размер 2 Ь] Ha . Здесь Ha — число Гартмана:

н. = B . bц .

У стенок, перпендикулярных магнитному полю, толщину сеточного слоя уменьшим до 2a Ha 0,5 ; у стенок, параллельных магнитному полю, возьмем 10 элементов. Для упрощения вычислений числа Гартмана (6) физические свойства — электропроводность с , плотность р , кинематическую вязкость v, половину высоты канала b зададим равными 1, а магнитную индукцию B будем варьировать в зависимости от требуемой

величины числа Гартмана. Это

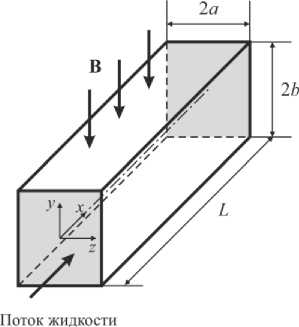
Рис. 2. Схема к решению задачи

допущение также позволяет снизить постоянную дифференцирования по времени уравнения (1) и производить меньше временных шагов. На всех стенках канала выполним условия прилипания жидкости, а на выходе будем считать давление нулевым и предположим возможным учет обратных потоков.

Полученные в вычислительных экспериментах результаты можно разделить на три группы: сравнение двумерных моделей, трехмерных моделей, времени счета в стандартных программных пакетах численного моделирования. Далее представлены данные, установленные с использованием: – предлагаемого решателя;

– стандартного решателя «mhdFoam», реализованного в OpenFOAM;

– аналитического решения для двухмерного случая согласно уравнению cosh (Ha ) - cosh (Ha- y/2Ь)

x ⁰ cosh ( Ha ) - sinh ( Ha/2 Ь ) ’

– коммерческих пакетов Comsol и ANSYS.

В выражение (7) входят величины: 2 b — высота сечения канала; y — координата вдоль направления магнитного поля; U и U — скорость в направлении распространения потока и ее характеристическое значение. Для всех случаев принято: число Рейнольдса Re = U^bj v = 1; магнитное Рейнольдса Re_m = стц_o ub <<  1; магнитное число Прандтля P_m = Re_m/Re <<  1.

• 3.1.    Сравнение двумерных моделей

Далее сравниваются результаты, полученные на основе двумерных моделей в предположении, что канал имеет бесконечную ширину. Такой подход позволяет верифицировать модель с помощью аналитического выражения (7), приведенного в работе [28]. На рисунке 3 а показаны распределения скорости между стенками, перпендикулярными магнитному полю, для чисел Гартмана 1 и 20, которые рассчитаны с использованием: встроенного решателя «mhdFoam» в программе OpenFOAM (на графиках обозначаются аббревиатурой OF); предлагаемого авторами решателя с использованием библиотеки EOF (на графиках EOF) и аналитического выражения (7). Численно установленные результаты демонстрируют хорошее совпадение с аналитическим решением.

Стоит отметить, что приложенное магнитное поле имеет однородное распределение по объему канала и слабо выраженную вихревую природу. В реальных задачах профиль скорости будет иметь другой характер, а аналитические решения, как правило, отсутствуют вследствие множества физических явлений, которые должна учитывать математическая модель. Эти выводы подтверждаются данными расчетов, показанными на рисунке 3 б , где, помимо двумерной задачи, представлена информация о решении на основе трехмерной постановки при различных граничных условиях на стенках канала:

• 1)    все стенки изолированы;

• 2)    стенки, перпендикулярные направлению магнитного поля, обладают бесконечной проводимостью, а стенки, параллельные магнитному полю, изолированы;

• 3)    все стенки обладают бесконечной проводимостью.

Поэтому для достижения цели верификации предлагаемого кода и оценки его точности важно осуществить расчеты при трехмерной формулировке задачи и разных граничных условиях.

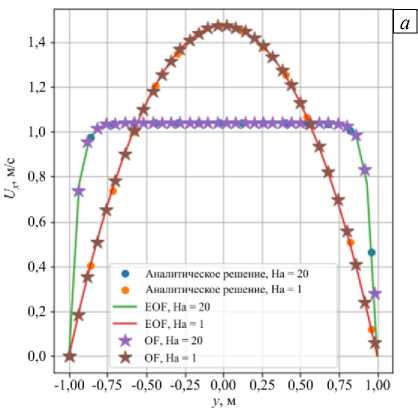
Рис. 3. К сравнению распределений скорости между стенками канала, перпендикулярными направлению магнитного поля при числах Гартмана 1 и 20: расчет с помощью стандартного решателя «mhdFoam» (кривые OF) и авторского решателя (EOF) в случае двумерной (2D) постановки задачи ( а ); расчет EOF при двухмерной и трехмерной постановках (для последней рассмотрены случаи граничных условий 1, 2, 3) ( б )

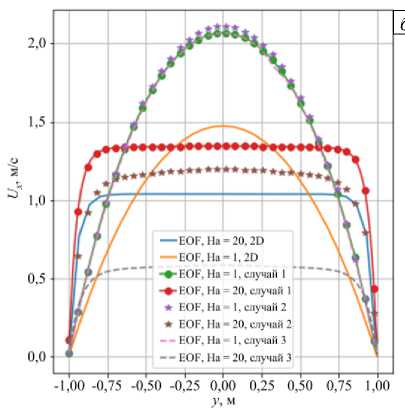
—EOF, На-20,2D

—EOF, На- 1,2D

-♦-EOF, На = 1, случай I

-♦- EOF, На = 20, случай 1

* EOF, На = 1, случай 2

* EOF. На = 20, случай 2

--EOF, На = 1, случай 3

— EOF, На = 20, случай 3

-1,00 -0,75 -0,50 -0,25 0,00 0,25 0,50 0,75 1,00 У» м

• 3.2.    Сравнение трехмерных моделей

Следующим шагом является верификация авторского решателя на трехмерной модели, которая позволяет учесть прилипание жидкости не только на стенках, перпендикулярных магнитному полю, но и на параллельных ему. Включение в модель условия прилипания является важным, потому что основным механизмом нестабильности течений в каналах является резкий рост сдвигового напряжения в пристеночных областях, который обусловлен именно прилипанием. Кроме этого, в трехмерной модели становится возможным учет вихревой природы поля скорости во всех пространственных направлениях, что является также важным для анализа течений в системах, на которые воздействует постоянное магнитное поле, а значит, для ответа на вопрос, как магнитное поле влияет на возникающие усилия.

А сравнение результатов расчетов в различных программных пакетах, в том числе с помощью предлагаемого кода, позволит оценить степень их точности. Распределения скорости между сверхпроводящими стенками показаны на рисунке 4. Отличие между кривыми, полученными стандартным решателем (OF) и с помощью библиотеки EOF менее 1% для чисел Гартмана 1 и 20. Данное расхождение может быть вызвано, с одной стороны, недостаточно точной расчетной сеткой в пристеночной области, где наблюдается наибольший градиент скорости, а с другой — методом интерполяции данных, участвующих в обмене между программами OpenFOAM и Elmer. Наибольшее отличие имеют результаты, вычисленные в ANSYS. Это можно объяснить спецификой модуля в ANSYS Fluent, предназначенного для решения задач магнитной гидродинамики. В данном модуле граничное условие необходимо разрешать конечными элементами, что приводит к уменьшению сечения канала с жидкостью на размер толщины стенки, заданный в настройках программы. В задачах, где эффект толщины стенки является важным, этот факт может помочь описать математическую модель более простым способом.

б

ьЧо

ANSYS, На ANSYS, На Comsol, На =

EOF, На = 1

аЧо

ANSYS. Ha

ANSYS, Ha

ANSYS, Ha

Comsol, Ha =

EOF, Ha = I

OF, На = 1

ANSYS, На

EOF, Ha= It

OF, Ha= 10

EOF Ha = 20

EOF, Ha

EOF, Ha

OF. На

EOF. Ha OF, Ha = OF, Ha = OF. Ha = OF. Ha =

-1,00 -0,75 -0,50 -0,25 0,00 0,25 0,50 0,75 1,00

j, м

Рис. 4. К сравнению распределений скорости в канале

с

и параллельны ( б ) магнитному полю

-1,00 -0,75 -0,50 -0,25 0,00 0,25 0,50 0,75 1,00 z, м изолированными станками: стенки перпендикулярны (а)

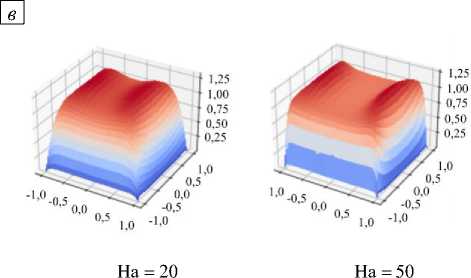
Пристеночный сдвиг слоев, как сказано ранее, вносит в течение нестабильность. В ряде задач магнитной гидродинамики, особенно при неидеализированных постоянных магнитных полях, где важную роль играет путь замыкания тока в пространстве и во времени, эти траектории могут иметь сложный характер, особенно на участках со значительным градиентом магнитного поля. Важным параметром в этих случаях является распределение плотности тока в канале, потому что его значение непосредственно влияет на распределение усилий. Один из способов оценки данной переменной — это построение для скорости линий одинакового уровня. На рисунке 5 представлены изолинии скорости в поперечном сечении канала при числе Гартмана, равном 10. Аналогичные результаты получены в работе [32], где изолинии имеют идентичный вид в обоих случаях условий на границах. На рисунке 6 изображены изолинии скорости для числа Ha = 50 , рассчитанные разными способами: с привлечением библиотеки EOF; стандартным решателем OpenFOAM; коммерческим пакетом ANSYS Fluent; аналитически [32]. Можно сделать вывод, что предлагаемый решатель на основе библиотеки EOF обеспечивает хорошую сходимость в сравнении с другими данными.

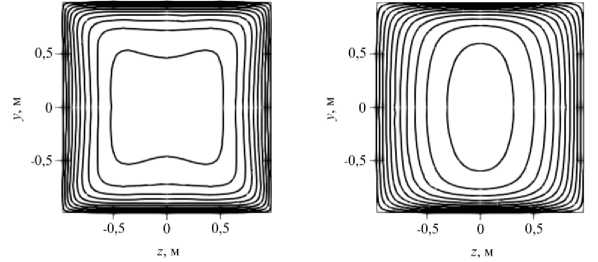
Рис. 5. Картины изолиний скорости в поперечном сечении канала: расчет с помощью библиотеки EOF ( а , б ), аналитическое решение [32] ( в , г ); стенки имеют бесконечную электрическую проводимость ( а, в ), изолированные стенки ( б, г )

Рис. 5. Продолжение

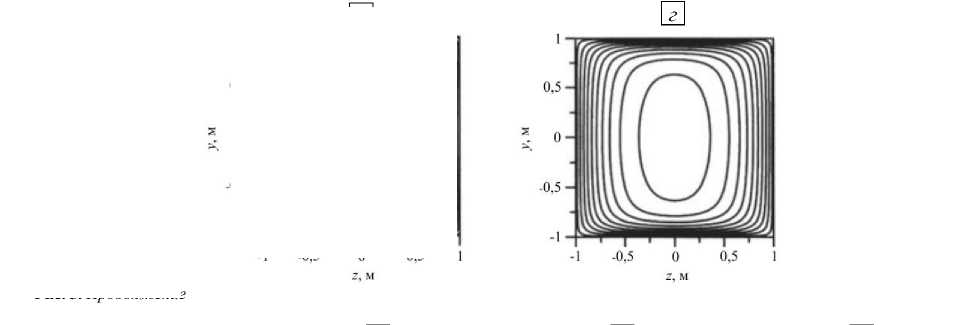
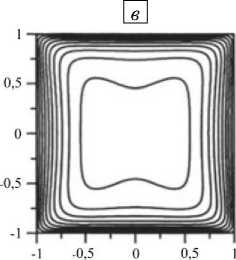
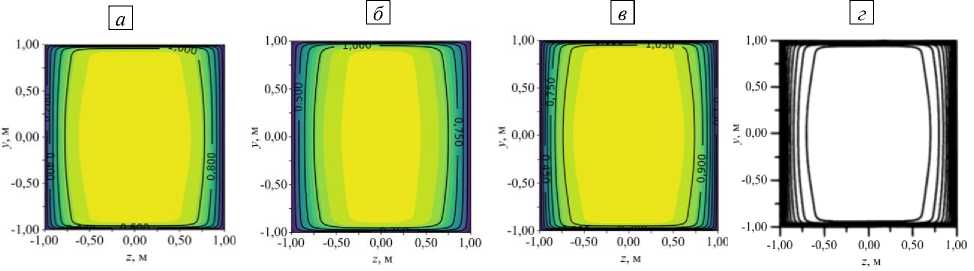
Рис. 6. Картины изолиний скорости в поперечном сечении канала для числа Гартмана, равного 50, полученные различными способами: авторским решателем с библиотекой EOF ( а ); OpenFOAM ( б ); ANSYS ( в ); аналитически [32] ( г )

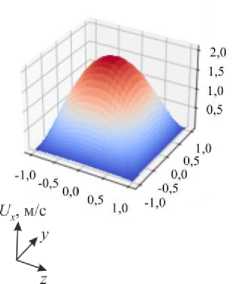
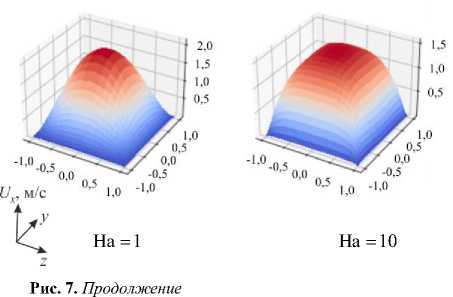
Последним этапом верификации предлагаемого кода является проведение качественного сравнения течения жидкости в постоянном магнитном поле для перечисленных выше трех основных случаев граничных условий [32]. На рисунке 7 представлены картины распределения скорости в поперечном сечении канала, которые качественно повторяют результаты хорошо известных в магнитной гидродинамике численных экспериментов, описанных, например, в [27] или [32].

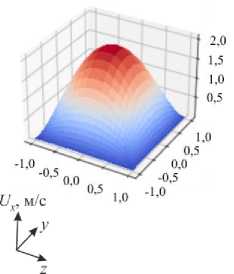
Ha = 1

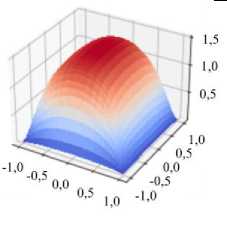
Ha = 10

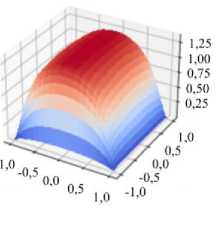
Ha = 20

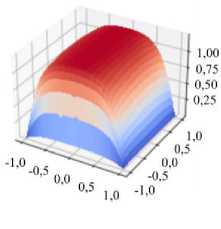
Ha = 50

Ha = 1

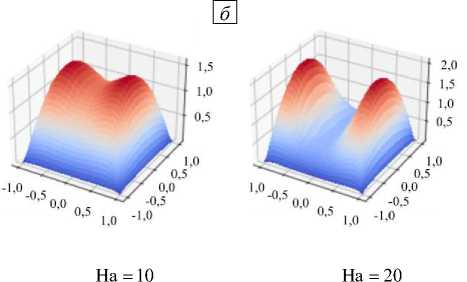
Рис. 7. Картины поверхностей равного уровня для скорости в канале при разных граничных условиях: все стенки выполнены из изоляционного материала ( а ); стенки, перпендикулярные направлению магнитного поля, обладают бесконечной проводимостью, а стенки, параллельные магнитному полю, изолированы ( б ); все стенки имеют бесконечную проводимость ( в )

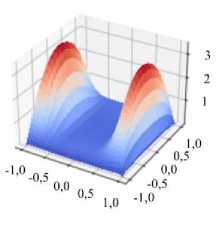
Ha = 50

• 3.3.    Сравнение времени счета

Продолжительность счета является важным критерием оценки производительности выбранного при моделировании математического представления задачи и метода решения. Приведем сравнительный анализ времени решения задачи Гартмана с помощью библиотеки EOF, встроенного решателя OpenFOAM и коммерческого пакета Comsol Multiphisics. Все три рассматриваемых варианта расчетов отличаются по используемым методам. Стандартный решать OpenFOAM — это чистый метод конечных объемов, библиотека EOF сочетает метод конечных элементов и метод конечных объемов, а Comsol Multiphysics — это чистый метод конечных элементов. Во всех случаях решение систем линейных уравнений, выбор схем дискретизации по пространству и времени осуществлялись согласно настройкам, установленным в перечисленных программных средствах по умолчанию.

Для расчета использовался канал с изолированными стенками, течение характеризовалось числом Гартмана, равным 10. Данные вычислений сведены в таблицу. Из таблицы видно:

– наилучший результат показывает стандартный решатель OpenFOAM. Но стоит отметить, что требующееся для расчетов время значительно повышается при рассмотрении неравномерных полей в пространстве, а также сокращение времени расчета при распараллеливании задачи. Однако решатель предназначен только для анализа постоянных полей и не имеет инструментов для моделирования неидеализированных систем, в которых необходимо учитывать конструкционные особенности источника поля, то есть к исследованиям течений жидкости в бегущем магнитном поле;

– производительность Comsol Multiphysics ограничена тем, что инструмент распараллеливания вычислений не представлен в явном виде и возможно применять только метод конечных элементов. Достоинством данного пакета является интуитивно понятный интерфейс, позволяющий создавать сложные мультифизические модели;

– предлагаемый авторами решатель устойчив и имеет хорошую сходимость результатов как при решении классических задач физики, так и при анализе реальных установок. Основной недостаток — это необходимость работы с двумя открытыми пакетами Elmer и OpenFOAM, которые используют разный программный синтаксис, а также может потребоваться знание языка программирования C++, если возникнет необходимость в изменении условий сочетания магнитной и гидродинамической задач.

Таблица. Время решения задачи течения жидкости в канале квадратного сечения в присутствии постоянного равномерного магнитного поля, перпендикулярного потоку жидкости

Программный пакет	Архитектура
	2 ядра	4 ядра	8 ядер	12 ядер
OpenFOAM	4 мин	2 мин	1,5 мин	1,5 мин
Библиотека EOF	33 мин	18 мин	12,5 мин	10,5 мин
Comsol	250 мин	–	48 мин	–
ANSYS	40 мин	–	30 мин	–

4.    Заключение

Осуществлена верификация, а также количественная и качественная оценка предложенного авторами кода для решения задач течения жидкости в присутствии постоянного магнитного поля в каналах прямоугольного сечения. Проведенные исследования показали, что отклонение между результатами, полученными с помощью авторского кода, и аналитическим решением [32] составляет не более 1%. Также проведено количественное сравнение распределений скорости между стенками канала с найденными другими способами: с использованием численных пакетов с открытой лицензией для расчета магнитного поля (Elmer), механики сплошных сред (OpenFOAM), библиотеки-связки этих пакетов (EOF-library) и коммерческих пакетов ANSYS и Comsol. Качественная оценка распределения скорости в поперечном сечении при различных граничных условиях на стенках канала произведена на примере трехмерной постановки задачи течения жидкости. Она также показала адекватность авторских результатов.

Оценка производительности различных численных пакетов выявила, что самую высокую скорость вычислений имеет стандартный решатель OpenFOAM, но он, в отличие от библиотеки EOF не позволяет производить сложные вычисления для электромагнитной задачи. Возможность осуществлять на основе библиотеки EOF квазистационарные вычисления электромагнитного поля являются еще одним ее преимуществом перед стандартным решателем OpenFOAM, который не работает с комплексными числами. Из слабых сторон предлагаемого кода можно выделить отсутствие встроенных модулей для расчета протекания тока в катушках со сложной замкнутой формой. Эти опции присутствуют в коммерческих программах Comsol Multiphysics и ANSYS. Исследована эффективность кода при распараллеливании вычислений с использованием библиотеки EOF в сравнении с другими программными пакетами. Обнаружено, что увеличение числа ядер при одинаковом объеме оперативной памяти приводит к сокращению времени счета более чем в 3 раза. Также открывается возможность настраивать отдельно распараллеливание магнитной и гидродинамической задач, а это может способствовать в будущем повышению производительности данного кода и расширению круга решаемых задач.

Резюмируя описанные выше результаты, можно утверждать:

• 1.    Проведенная верификация предлагаемого кода показала адекватность получаемых с его помощью решений.

• 2.    Самая высокая устойчивость решения при одинаковых сетках демонстрирует код в совокупности с библиотекой EOF.

• 3.    При использовании EOF-library и языков программирования C++ и Fortran можно создавать уникальные граничные условия.

• 4.    На абсолютные значения скорости в канале значительное влияние оказывают электромагнитные граничные условия.

• 5.    Предлагаемый код не ограничивается возможностью решения ламинарных течений под действием постоянного магнитного поля, а имеет более широкий круг применений, ряд из них можно найти в работах [20, 21, 31].

Также стоит отметить, что дальнейшие работы будут посвящены исследованию влияния бегущего магнитного поля на распределение скорости в индукционном насосе.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 20-38-90237.