Вероятность безотказной работы зубчатых цилиндрических передач: глубинная контактная выносливость

Безотказность является составным критерием оценки надежности зубчатых передач. Безотказность зубчатой передачи подразумевает способность непрерывно сохранять свою работоспособность за установленный срок службы. Для количественного определения безотказности передач выполняется расчет вероятности безотказной работы, основанный на вероятностатистических методах. Ввиду того, что существуют различные виды отказов зубчатых передач, вероятность безотказной работы можно определить по различным критериям. К отказам зубчатых передач и критериям безотказной работы относятся: поломка зубьев - изгибная выносливость; выкрашивание рабочих поверхностей зуба - контактная выносливость; глубинное выкрашивание рабочих поверхностей зуба - глубинная контактная выносливость; абразивный износ -износостойкость; заедание - противозадирная стойкость.

Первые три критерия являются наиболее важными критериями безотказной работы поверхностно-упрочненных зубчатых передач. Расчет вероятности безотказной работы по критерию изгибной и контактной выносливости разработан с достаточной глубиной и при корректном определении погрешности взаимного положения зубьев позволяет получить расчетные данные, согласующиеся с экспериментальными данными [1].

Глубинная контактная выносливость - это способность материала зуба сопротивляться циклическим напряжениям (глубинным контактным напряжениям) внутри зуба. Напряжения внутри зуба являются следствием напряжения на площадке контакта, сил трения между зубьями и остаточных напряжений в теле зуба. Расчет глубинных контактных напряжений у инженеров и исследователей строится на положениях теории сопротивления материала.

В основе методики расчета на предотвращение глубинного контактного разрушения, представленной в ГОСТ 21354-87 [2], лежит гипотеза Геста-Мора: определение касательных напряжений с учетом положительного влияния нормальных напряжений. Гипотеза также используется в методиках расчета на определение минимального коэффициента запаса прочности по глубине упрочненного слоя зуба в [1, 3, 4].

Влияние остаточных напряжений в упрочненном слое зуба учитывается в [5]. Методика использует подход, предложенный Финдли [6], суть которого заключается в том, что существует плоскость в теле зуба, на которой при максимальном нормальном напряжении амплитуда касательных напряжений максимальна. В этой критической плоскости определяется эффективное напряжение. В расчетах используется параметр материала зуба, который именуется критерием Финдли. Критерий в [7–9] имеет другие расчетные формулы и носит наименования: критерий Данг Вана или критерий Матаке. В основном расчет сводится к определению точки по глубине упрочненного слоя зуба с минимальным коэффициентом запаса прочности [10], с последующим определением в этой точке усталостного ресурса передачи [11].

В [12] расчет действующих эффективных напряжений по глубине упрочненного слоя основан на обобщенном критерии предельного состояния Лебедева-Писаренко [13] для структурно неоднородного материала.

В исследовании [14] распределение напряжений и зоны пластической деформации оценивались с помощью упругопластической модели для пластически градиентных материалов. Модель подробно описана в [15]. Эквивалентная пластическая деформация при расчете определяется по Мизесу путем численного моделирования (методом конечных элементов) напряжений по глубине упрочненного слоя.

Также существуют методики [16, 17], определяющие лишь глубину опасной зоны, соответствующей максимальному значения отношению эквивалентных напряжений (по принятому критерию) к твердости по Виккерсу, при этом не пытаясь определить какие-либо качественные значения (коэффициент запаса прочности, ресурс передачи и др.).

В рассмотренных выше методиках расчета, а также [18-20] не было обнаружено создания методики расчета вероятности безотказной работы по критерию глубинной контактной выносливости.

Цель статьи - разработать методику расчета вероятности безотказной работы поверхностно-упрочненных зубчатых цилиндрических передач по критерию глубинной контактной выносливости.

Методика расчета вероятности безотказной работы по критерию глубинной контактной выносливости

В общем виде вероятность безотказной работы зубчатых передач, при известных функциях плотности распределения фактических напряжений и допускаемых, сводится к определению интеграла:

P =

Р_а ⁽ а + otm) • Р_аit^ot_lm)dot_im

d о,

где o , o _tt_m - фактические и допускаемые напряжения; o _m - максимальное допускаемое напряжения; Р_а, Р_{с t}t_m - функции плотности фактических и допускаемых напряжений.

Для определения фактических и допускаемых напряжений используем расчетные формулы из методики [21], основанной на критерии предельного состояния Лебедева-Писаренко. Выбор формул основан на проведенном анализе и валидации существующих методик расчета глубинной контактной выносливости цилиндрических передач [22].

Действующее эффективное напряжение а рассчитывается по формуле, МПа:

I о'1 + а'2+а'з| o = /Ot + (1- z)O!л1     ci   I,                                                         (2)

где X – параметр пластичности материала; (J_t – интенсивность октаэдрических напряжений, МПа; °"1 , 0*2 , 0"₃ – главные напряжения, МПа; A – статистический параметр дефектности для закаленных сталей = 0,7 ÷ 0,8.

Пластичность материала X имеет функциональную зависимость от твердости материала и вида ХТО:

– цементация

X = -0,89 Hrv ∙10 ~³ + 1,356, Xmtn = 0,6,                                               (3)

– нитроцементация

X = -0,71 Hhv ∙10 ~³ + 1,284, Xmin = 0,68,                                             (4)

где H_Hy – твердость стали по Виккерсу (при H_hv ≤400 X =1 ).

Напряжения Oi , ^2 , (7g определяются через компоненты O_x , °y , °z , ^Txy , Ty_Z , T-ZX контактного напряжения °H , связанные кубическим уравнением:

o3 - I-vO2 + 12° - I3 =0, (5) где 1-^ , ^2 , /3 – коэффициенты уравнения, рассчитываемые по формулам: II =   + Oy + Oz , I2 =      + ^y^z + OzOx - txy - Tyz - T-zx, I3 =        +2 ^xy^-yz^-zx - Ox^-yz - Oy^zx - Oz^-xy․ Индексация главных напряжений – корней уравнения (5) – определяется через условие: (6) (7) (8) o'! ≥ °1 ≥ o3 .

Компоненты °x , Oy , O_z , ^Txy , Tyz , ^ZX контактного напряжения °H для случая первоначального контакта двух цилиндров по линии рассчитываются по формулам [23]:

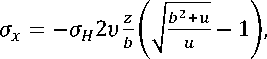
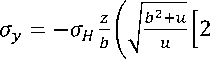
i r2 h2  1 -2

ii2 + b2z2\

bz3 b2+u

^Z =- z        n ll2 + b2z2 Aj U

Ty_Z=- °H

byz2 u2+b2z2

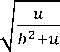
где X,Z – координаты точки на площадке касания (рис. 1), мм; b – полуширина эллиптической площадки касания (см. рис. 1), мм; V – коэффициент Пуассона; и – корень уравнения    +=

1 . Напряжения T_xy , ^zx принимаются равными нулю.

Интенсивность октаэдрических напряжений определяются по формуле, МПа:

=√   ( O1 - 2 ) ~2 +( °2 - O3 )2 +(O3 - O1 )2․

Допускаемые эффективные напряжения определяются по формуле, МПа:

О Um = (X - 0,11128)^HV^LK ∏1=1 ^i, где ^LK – коэффициент долговечности; ^1 – коэффициент, зависящий от характера контактирования (для линейного контакта ^1 = 2,05 ÷ 2,15); ^2 – коэффициент, зависящий от числа «зон риска» в пределах упрочненного слоя (при наличии одной зоны ^2 =1, двух зон –^2 =0,90÷ 0,95); ^3 – коэффициент, учитывающий влияние внешней касательной нагрузки; /С4 – коэффициент, учитывающий качество материала и ХТО (для углеродистых и низколегированных сталей, не содержащих никеля /С4 =0,90÷0,95, для легированных сталей с содержанием никеля до 1 % /С4 =0,95÷1,05, для никельсодержащих сталей/С4 = 1,05 ÷ 1,10).

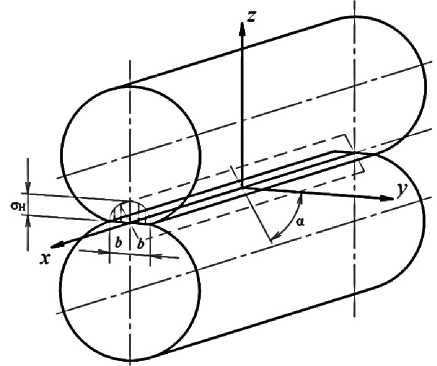
Рис. 1. Расчетная схема контактных напряжений двух параллельных цилиндров

Коэффициент долговечности ^■LK вычисляется по формуле:

Zlk ₌        ,                                                                                (15)

где Nek – эквивалентное число циклов перемены напряжений.

Коэффициент ^3 имеет функциональную зависимость координаты :

=                               , l+^l+60C8,i5f2T,s-i](l+z°)"8 , ,

где Cap – отношение профильного радиуса к продольному, Cap =0 (линейный контакт); f – коэффициент трения; Z° – относительная координата z ( Z° =/ b ) .

При выполнении расчетов на сопротивление глубинной контактной усталости используется функция распределения твердости по глубине упрочненного слоя. Существует множество различных функций распределения твердости [24–26], используемых инженерами и исследователями, при расчетах зубчатых передач. Авторами данной статьи была оценена точность существующих функций распределения твердости по глубине упрочненного слоя рабочих поверхностей зубчатых передач на основе известных экспериментальных данных. В результате оценки точности были выбраны следующие уравнения, используемые в описываемой методике:

– при цементации

HV ( Z )= н_од ( z )+ h_c( 1- g ( z )), где

g ^(z)=1-3&+2 V5 ;

– при нитроцементации л           HV (z)(Hmax Hp)(8c-z)

⎧                  ⁼         ,       ⁺

⎪ ₊ Hq при 0< Z ^≤ Z-max

⎨ HV ( z )=( H_c - H_o ) [ 8_C ехр 1- 5c ^] + ^,

⎩+ Hq при Z-max ^< Z ^≤ 8c где

В =ln(^)fln f^exp^^^)] ․

V H_c-H₀ J V \ 8_C^p 8_C /J

В (17)–(20) приняты следующие обозначения: ^0 – твердость поверхности зуба; Нщах – максимальная твердость упрочненного слоя; ^eff – эффективная твердость упрочненного слоя; He – твердость сердцевины; Zmax – глубина максимальной твердости упрочненного слоя; ^zeff – эффективная толщина упрочненного слоя; ẟ_c – толщина упрочненного слоя (расстояние от поверхности до сердцевины).

Для расчета вероятности безотказной работы по критерию контактной или изгибной прочности функция фактических напряжения будет зависеть только от переменной величины крутящего момента. Однако в случае расчета глубинной контактной выносливости фактические напряжения зависят от контактных напряжений н_н и изменяются по глубине упрочненного слоя. При этом с изменением контактных напряжений н_н меняется и координата минимального коэффициента запаса прочности SH = lт/ н , так как компоненты объемного напряженного состояния внутри тела зуба зависят от величины площадки контакта (9)–(12), размер которой коррелирует с контактными напряжениями н_н . Предел выносливости также будет изменяться по глубине упрочненного слоя из-за изменения его твердости. На рис. 2 представлен график изменения координаты расположения точки s_HHmin с минимальным коэффициентом запаса прочности SH в зависимости от изменения контактных напряжений н. .

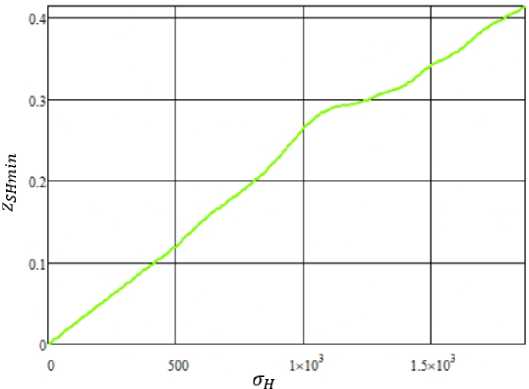
Рис. 2. График изменения координаты расположения точки z_SHmln с минимальным коэффициентом запаса прочности в зависимости от изменения контактных напряжений н_н

В результате для создания методики расчета вероятности безотказной работы зубчатых передач по критерию глубинной контактной выносливости был взят за основу подход, предложенный в [27], для расчета вероятности безотказной работы корпуса трубопроводной арматуры по критерию прочности. Суть подхода в том, что с помощью численного моделирования определяется набор опасных (по критерию прочности) точек корпуса, далее для каждой точки получают функцию напряжений и рассчитывают вероятность безотказной работы. Вероятность безотказной работы корпуса оценивается точкой с минимальным значением.

Стоит отметить, что есть и другой вариант решения поставленной задачи: нужно решить задачу оптимизации для функции двух переменных SH(z,н_H) ^ тIn, используя методы нелинейного программирования. Затем рассчитать вероятность безотказной работы для z_SHmin , полученного на предыдущем этапе. Это вариант расчета был отклонен по причине того, что, велика вероятность возникновения овражных, седловых зон на функции SH(z, н_н) , потребуется постоянный контроль при расчетах (вывод отображения функции SH(z, н_н) ) и применение громоздких алгоритмов при реализации методов оптимизации.

На рис. 3 представлен алгоритм расчета для определения вероятности безотказной работы по критерию глубинной контактной выносливости.

Основные блоки алгоритма на рис. 3 пронумерованы. Остановимся подробнее на каждом из них.

Блок 1 (см. рис. 3) предназначен для ввода исходных данных. Выборка контактных напряжений, необходимая в исходных данных, либо передается из расчета вероятности безотказной работы по критерию контактной выносливости, либо генерируется датчиком случайных чисел с указанием типа функции плотности распределения контактных напряжений и ее параметров. Также в исходных данных необходимо указать параметры поверхностного упрочнения зубьев, модуль упругости, коэффициент Пуассона и приведенный радиус кривизны в полюсе зацепления.

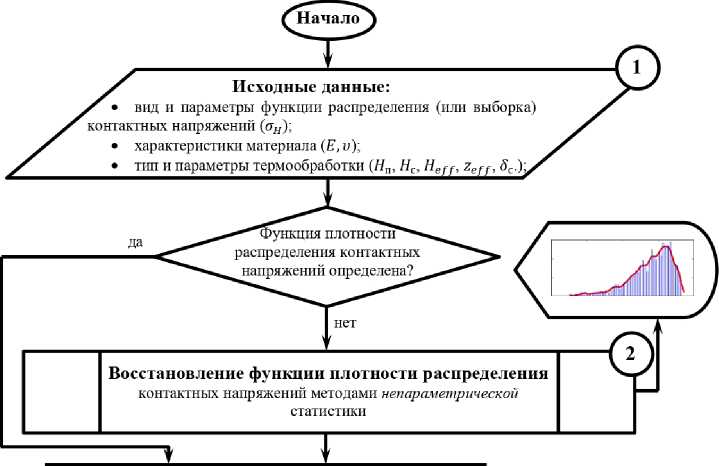
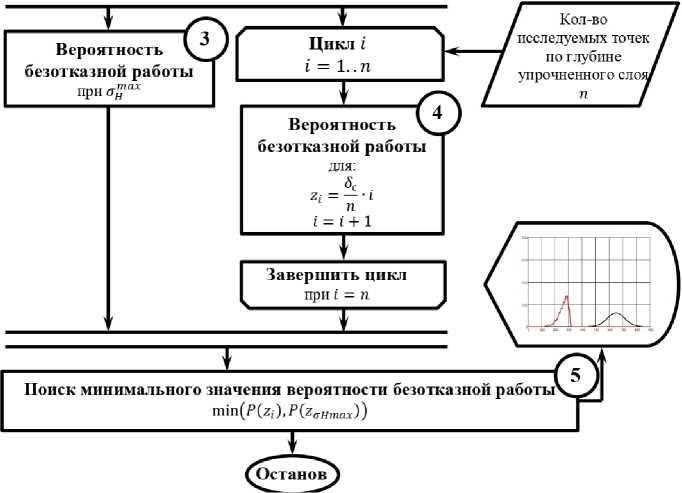
Рис. 3. Алгоритм расчета для определения вероятности безотказной работы по критерию глубинной контактной выносливости

На основе полученной выборки контактных напряжений в блоке 2 (см. рис. 3) нужно определить закон распределения контактных напряжений, используя методы непараметрической статистики [28]. Блок 2 представляет собой отдельную программу, если функция плотности распределения известна, то блок 2 пропускается в расчете.

Блоки 3 и 4 выполняют расчеты параллельно, используя формулы (1)–(20). Блок 3 рассчитывает вероятность безотказной работы при максимальном значении контактного напряжения из полученной выборки, при этом координату z_{SHm in} для расчета определяют как координату, для которой функция коэффициента запаса прочности ( )→ . В блоке 4 выполняется расчет вероятности безотказной работы для всех координат z_t ( I = 1.. и ), равномерно распределенных по глубине упрочненного слоя, количество и которых задается пользователем. Разброс значений (коэффициент вариации) допускаемого глубинного напряжения на глубине меньше эффективной толщины упрочненного слоя принимается равным 5 %, на большей - 10 % [12].

В блоке 5 (см. рис. 3) определяется минимальное значение вероятности безотказной работы, из полученных в блоках 3 и 4 и выводится график плотностей распределения фактических и допускаемых контактных напряжений.

Результаты расчетов

Используя представленный алгоритм, выполним расчет вероятности безотказной работы для зубчатой цилиндрической передачи, параметры которой представлены в таблице.

Таблица

Параметры зубчатой передачи

Параметр	Значение
Модуль, мм	10,5
Число зубьев: – шестерни – колеса	12 53
Приведенный радиус кривизны в полюсе зацепления, мм	94,605
Угол наклона зубьев, град	0
Эквивалентное число циклов нагружения	1,13238 ∙ 10 8
Материал	12ХН3А
Поверхностное упрочнение	цементация
Твердость поверхности зуба, HV	600
Твердость сердцевины, HV	320
Эффективная твердость, HV	550
Общая толщина упрочненного слоя, мм	2
Эффективная толщина упрочненного слоя (по ГОСТ 21354-87), мм	1,007
Модуль упругости, МПа	2,15 ∙ 10 5
Коэффициент Пуассона	0,3

Выборка контактных напряжений (рис. 4) получена в результате расчета контактной выносливости по методике [29]. Напряжения получены для выборки крутящего момента при номинальном значении 5 кН ∙ м и функции плотности β-распределения ( a = 6, b = 2 ), что соответствует тяжелому режиму работы зубчатой передачи [29].

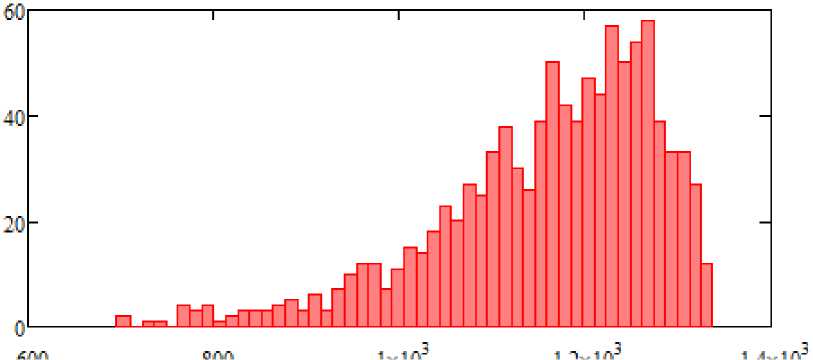
Рис. 4. Выборка контактных напряжений

На рис. 5 представлены результаты вычислений вероятности безотказной работы для заданных координат z.

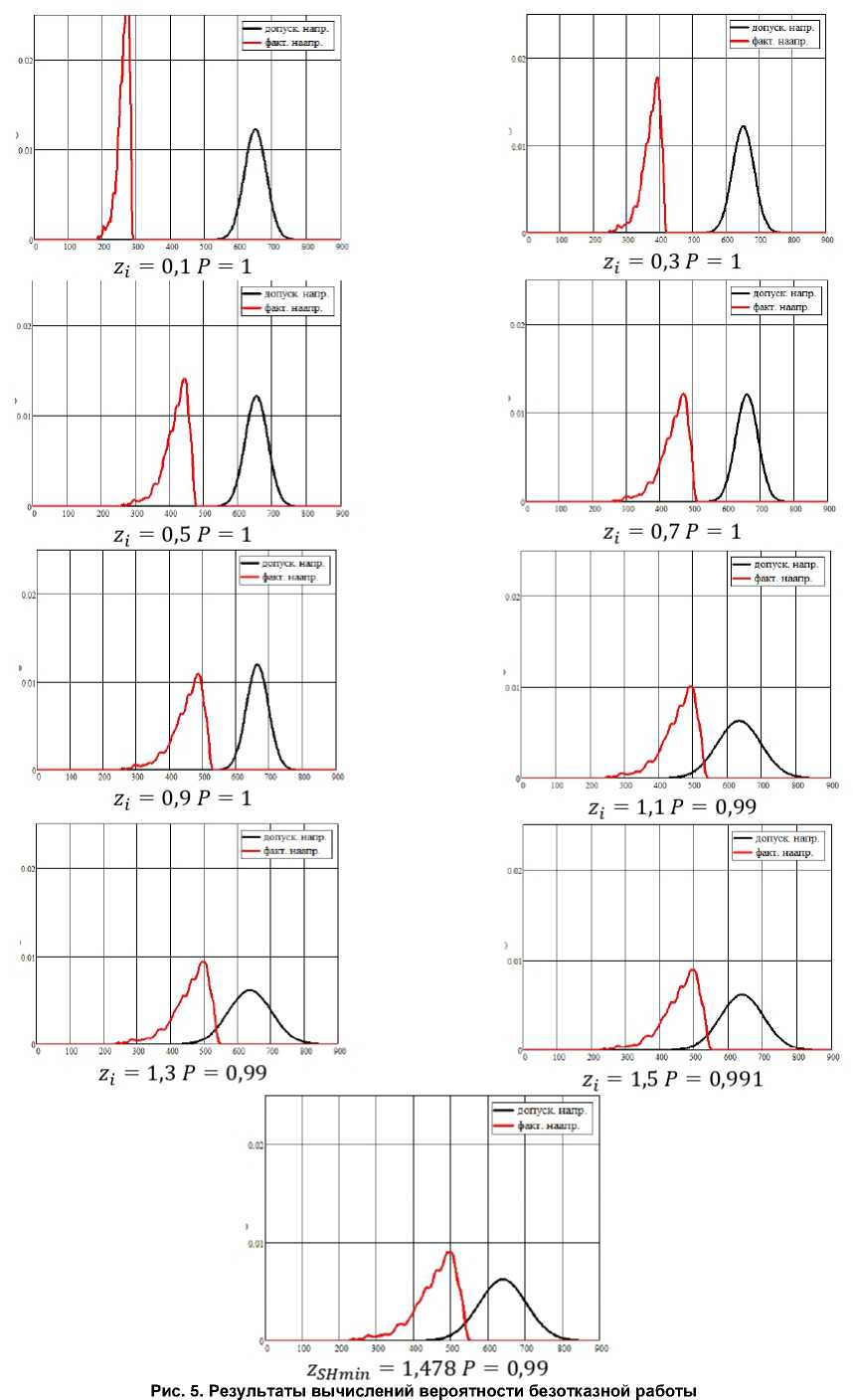
по критерию глубинной контактной выносливости

В результате расчета вероятность безотказной работы по критерию глубинной контактной выносливости принимается Р=0,99 .

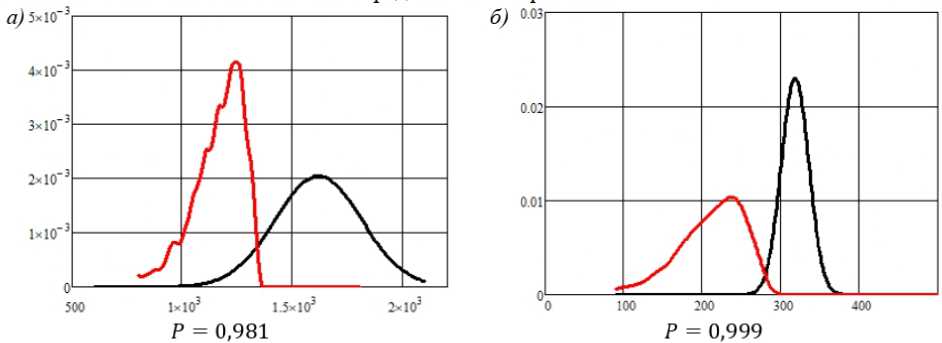
Рис. 6. Вероятность безотказной работы зубчатой передачи при 5 кН ∙ м по критерию: а) контактной выносливости; б) изгибной выносливости

Сравним вероятность безотказной работы по всем трем критериям (рис. 6), можно заключить, что лимитирующим фактором работоспособности передачи является контактная выносливость. Однако при увеличении номинального крутящего момента до 6 кН ∙ м характер влияния критериев на работоспособность зубчатой передачи изменяется (рис. 7).

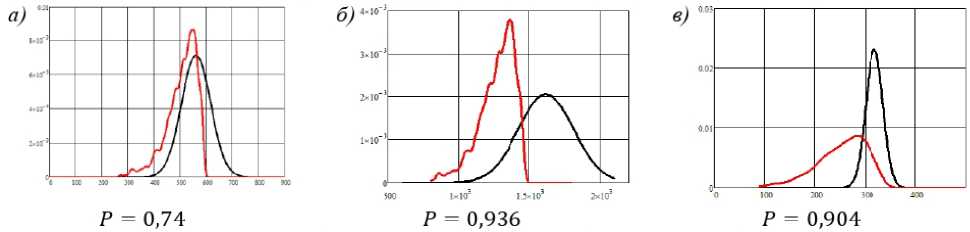
Рис. 7. Вероятность безотказной работы зубчатой передачи при 5 кН ∙ м по критерию: а) глубинной контактной выносливости;

б) контактной выносливости; в) изгибной выносливости

С увеличением крутящего момента вероятность безотказной работы по критерию контактной выносливости показало наименьшее снижение, по критерию изгибной выносливости значение снизилось до удовлетворительного. Вероятность безотказной работы по глубинной контактной выносливости стала значительно ниже, что делает ее лимитирующим фактором работоспособности для рассчитываемой зубчатой передачи.

Выводы

• 1.    Разработана методика расчета вероятности безотказной работы зубчатой цилиндрической передачи по критерию глубинной контактной выносливости с применением методов непараметрической статистики.

• 2.    На основе разработанной методики был выполнен расчет вероятности безотказной работы зубчатой цилиндрической передачи при номинальных крутящих моментах в 5 кН ∙ м и 6 кН ∙ м .

• 3.    Сравнение результатов расчета со значениями вероятности безотказной работы рассчитываемой передачи по критериям контактной и изгибной выносливости показало, что при увеличении крутящего момента лимитирующим фактором работоспособности передачи становится глубинная контактная выносливость.

• 4.    Разработанная методика может служить частью методологии проверочного расчета зубчатых цилиндрических передач численными методами моделирования (метод Монте-Карло).

• 5.    Взаимосвязь значений вероятности безотказной работы по различным критериям, а также основные факторы влияния на их значение, требует дальнейшего исследования.