Вероятность сноса оценок параметров межкадровых геометрических деформаций изображений при псевдоградиентном измерении
Автор: Ташлинский Александр Григорьевич, Воронов Илья Васильевич
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Статья в выпуске: 6-2 т.16, 2014 года.
Бесплатный доступ
В работе рассмотрена методика расчета вероятности сноса оценок параметров межкадровых деформаций, формируемых псевдоградиентными процедурами при оценивании одного и нескольких параметров.
Цифровое изображение, межкадровые деформации, вероятность, снос, псевдоградиентная процедура
Короткий адрес: https://sciup.org/148203595
IDR: 148203595 | УДК: 004.932.4
Текст научной статьи Вероятность сноса оценок параметров межкадровых геометрических деформаций изображений при псевдоградиентном измерении
Под псевдоградиентным измерением вектора a неизвестных параметров в работе понимается использование для получения оценки a рекуррентной процедуры вида [1]:
"a -1 + 1 =a t - Л t + 1 P t + 1 ( q ( z , <a t )) , (1)
Для вектора a = ( a 1 , a 2,
. ...
T
, a m ) парамет-
где Р t + 1 ( q ( z , a t )) - псевдоградиент (ПГ) целевой функции (ЦФ) Q , Z - наблюдаемые изображения, для которых требуется оценить параметры a ; Л t + 1 - матрица усиления. В общем случае Р t + 1 ( q ( z , a t )) — это случайное направление в пространстве параметров, определяемое значениями a t и номером итерации t . Это направление будет считаться ПГ ЦФ в точке a пространства параметров, если будет выполнено условие:
[ V Q ( a ) ] T M{ p ( Q ( z , a )) > 0 ,
ров межкадровых геометрических деформаций изображений (МГДИ) соотношение (1) можно представить в виде:
(^ t + 1 =(a t - Л t + 1 ф t + 1 ( v q ( z (1) , z (2) , (^ t ))=a t +^a t + 1
,
где ф t + 1 - некоторая векторная функция от градиента на t -й итерации; Z (1) , Z (2) - наблюдаемые изображения. Для уменьшения вычислительных затрат в выражении (2) допустимо использование вместо V Q ( z (1) , Z (2) , a t ) его усе-
чение
‒
v q ( z t + 1 , а. ) ,
где
то есть, если направление ₽ ( Q ( * ■, a )) в среднем составляет острый угол с направлением вектора градиента V Q (а) функционала Q ( a ) . Применение ПГ алгоритмов в современных системах весьма обоснованно их хорошими точностными характеристиками и устойчивостью к широкому классу помех наряду с вычислительной простотой и отсутствием требования к предварительной оценке параметров исследуемых изображений.
Воронов Илья Васильевич, аспирант
7 — L(1) 7(1) 7(2) ,= y(2) I
z t + 1 = 1 ? ^ e Z , z j e Z } - двумерная локальная выборка ЦФ на t -й итерации. При выборе знаковой функции sgn( ° ) в качестве векторной функции от градиента ф получаем простые и хорошо сходящиеся алгоритмы релейного типа [2, 3] Р t + 1 = sgn (v q ( z t + 1 , a t )) , где sgn( x ) = ( sgn( x 1),...,sgn( X m ) ) T .
Вероятность сноса оценок при измерении одного параметра. Асимптотические вероятностные свойства оценок, сформированных псевдоградиентными процедурами, хорошо изучены. Возможности же анализа вероятностных свойств оценок (X t при конечном числе итераций исследованы недостаточно. Объясняется это большим числом факторов, влиянием которых нельзя пренебречь. К таким факторам можно отнести характер плотности распределения вероятностей (ПРВ) и ковариационную функцию (КФ) изображений, мешающий шум, вид ЦФ Q,
выбор функции ф t преобразования градиента и матрицы усиления Λ t , определяющей величину t -го шага, общее число итераций T и начальное приближение а о вектора а . Эти факторы можно условно разделить на две группы [4]. Первую группу сформируют факторы, которые заданы априорно и не зависят от вида ПГ процедуры. К ним относятся ПРВ и КФ изображений, мешающий шум, а также ЦФ оценивания Q . Во вторую группу войдут факторы, на которые можно воздействовать при использовании ПГ процедур. Сюда можно отнести вид функции ф t , матрицу усиления Л t , начальное приближение а о вектора а и число общее число итераций T . Большой набор влияющих факторов в обеих группах создает сложности анализа эффективности ПГ процедур при конечном числе итераций.
Учитывая то, что в (2) для получения текущей оценки а i , t + 1 предполагается дискретное изменение предыдущей оценки а i , t , в качестве величин, комплексно характеризующих влияние факторов первой группы, предлагается использовать вероятности изменения оценки исследуемых параметров на каждой итерации. Данные вероятности характеризуют переход состояния вектора а параметров из t -го состояния в ( t +1)-е состояние. При этом из-за дискретного изменения оценки а i , t на ( t +1)-й итерации для ПГ процедуры возможны только три события:
- Изменение оценки направлено в сторону истинного значения параметра, тогда:
sgn( S i, t) = sgn Аа i, t+1 , где S i,t = а iu -аi,t, i = 1, m - рассогласование истинного значения параметра аi и его оценки на t-й итерации. При этом направление проекции псевдоградиента на ось параметров а i совпадает с истинным направлением проекции градиента. Вероятность такого события обозначим Р + ( St ) .
̶ Изменение оценки имеет направление от истинного значения:
Sgn( Si,t) = - Sgn Ааi,t+1 .
Вероятность такого события обозначим р i ( S t ) . При этом событии направление проекции псевдоградиента на ось параметров а i противоположно истинному направлению проекции градиента.
̶ Нулевое изменение оценки. Не происходит никакого изменения оценки, при этом Аа i , t = 0. Вероятность такого события обозначим р 0 ( S t ). Очевидно, что вероятности р + ( S t ) , р 0( S t ) и р i ( S t ) составляют полную группу событий:
Р + (St ) + Р - (St ) + Р0(St ) =1
Таким образом, при максимизации ЦФ ПГ процедуры для случая S i , t > 0 , p + ( S t ) - это вероятность того, что на ( t +1)-й итерации проекция псевдоградиента р i на ось параметров а z будет отрицательной:
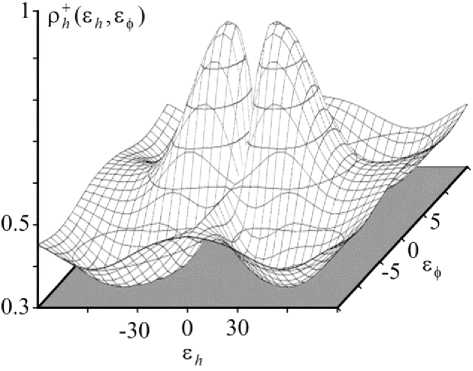
Р +(S,) = P{Pi<0}= 0 w(p,(z -^ где w(вi (Z(1), Z(2), аi,t-1)) - ПРВ проекции рi на ось параметров а i. Для случая минимизации ЦФ р+ (St ) - характеризует вероятность того, что на (t+1)-й итерации проекция псевдоградиента Pz на ось параметров а i окажется положительной: Вероятности р+ (St ) и рi(St ) будем называть вероятностями сноса оценки (ВСО) i параметра аi. Используя плотность распределения вероятности р+ (S) = {Р + ( St ),рi(St ),р0 (St)}несложно получить явные выражения для ПРВ оценок параметров а . В частности, при оценивании параметров изображений для этого удается использовать свойство нормализуемости проекции градиента ЦФ на ось исследуемого параметра при объеме двумерной локальной выборки ЦФ больше двух [5]. В качестве примера на рис. 1 приведены графики функции Рz+ (|St ) для параллельного сдвига при объеме локальной выборки ЦФ ц=1, 3, 5, 10 и 20. Там же показаны экспериментальные результаты, полученные статистическим моделированием по 500 реализациям на имитированных гауссовских изображениях с аналогичными параметрами. Пример имитированного гауссовского изображения, используемого при моделировании, приведен на рис. 2. Анализ показывает хорошее соответствие теоретических и экспериментальных результатов при ц>3. Рис. 1. Вероятность сноса оценки для параллельного сдвига Рис. 2. Пример имитированного изображения Рис. 3. Вероятность сноса оценки сдвига при оценивании двух параметров Если оценки искомых параметров зависимы, например, при оценке сдвига h и угла поворота ф, то величина рh (£h, £ф) при определенном сочетании значений ε может быть и меньше 0,5. Оценки некоторых отдельных параметров в ходе работы ПГ процедуры могут ухудшаться при улучшающихся оценках ЦФ. Пример такого случая приведен на рис. 3. Полученная с помощью ПГ процедуры (2) последовательность оценок a0,al,..., at,..., aT вектора параметров α , является m-мерной марковской цепью. Для релейных алгоритмов элементы матрицы условных вероятностей переходов из состояния l в состояние t легко могут быть выражены через переходные вероятности р+(£t), р 0( £t ) и рi( £t ). В [6] получены выражения для одношаговых ПРВ переходов оценок. Однако при большой размерности вектора параметров α резко возрастает требование к вычислительным ресурсам. Основными факторами, определяющими требования к вычислительным затратам, являются число возможных значений оценки каждого параметра и размерность вектора оцениваемых параметров. Проанализируем возможности уменьшения объемов вычислений для данных факторов. Вероятность сноса оценок при измерении набора параметров. Разобьем область определения Ωα возможных значений параметра a i вектора a на подобласти ®i,k , к = 1, Ki , поставив в соответствие каждой юi,к фиксированное значение ai,к е гоi,к . При этом ai внутри каждой подобласти гоi,к будем считать неизменным. Такой переход от непрерывной области определения Ωα к дискретной позволяет априорно выбрать размеры kπ×kπ, kπ =∑mKi, мат-i=1 рицы пi(t) = ||п(i)к,j(t)| одношаговых переходов, обеспечивающие реализуемость вычислений при заданном классе вычислительных средств. Далее воспользуемся тем обстоятельством, что на t-й итерации из состояния ai,j оценки параметра αi вне зависимости от состояния других оценок, можно перейти только к состояниям ai, к, где к e{j+vi, t + 1, j+vi, t,j,j - vi, t, j - vi, t-1}, vi,t = int (^i,t / ^ i), ^ i - шаг дискретизации области определения параметров αi . Вероятности указанных переходов определяются состоянием оценок других параметров и являются матричными функциями. Каждая подобласть гоi,к, i = 1, m, k = 1, Ki , пространства оценок параметров имеет свои вероятности переходов. Суммируясь, они дают общую вероятность перехода оценки аi из состояния ai, j в состояние ai,к . Так для двух параметров а1 и a 2 общую вероятность улучшения оценки ai = a 1, j на t-м шаге можно выразить как: K1 7 X Р+ = 1 — Z Р2к (t — 1)Р — (^17,82к ) = к=1 , = pT (t - 1)p (8I j , 82 ) где p2к (t-1) = P(а2 = a2к ), к = 1, K2 - вероятность того, что на (t- 1)-й итерации величина а2 имеет значения a 2к; £ i,j = ai, j —a - погрешности оценки. Аналогичные соотношения возможно записать и для большего числа m параметров. Соответственно будет модифицирована матрица одношаговых переходов пi(t) для параметра mm ai, размер которой сократится с 2 Ki х Z Ki i=1 i=1 до Ki х Ki. Однако, указанное сокращение размерности достигается ценой потери информации о вероятности нахождения оценки вектора параметров а на t-й итерации в каждой из подобластей юi. Сохраняются только проекции этого пространственного распределения на оси параметров. Но этого достаточно для решения по- ставленной задачи. Невозможно только однозначно восстановить распределение вероятностей в пространстве параметров. Исследование выполнено при финансовой поддержке государственного задания Минобрнауки России № 2014/232 и гранта РФФИ № 15-41-02087.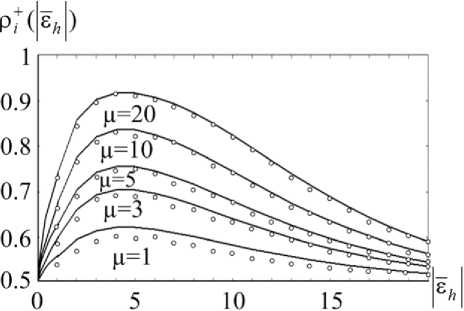

Список литературы Вероятность сноса оценок параметров межкадровых геометрических деформаций изображений при псевдоградиентном измерении
- Цыпкин, Я.З. Информационная теория идентификации. -М.: Наука, Физматлит, 1995. 336 с.
- Ташлинский, А.Г. Псевдоградиентное оценивание пространственных деформаций последовательности изображений//Наукоемкие технологии.2002. Т. 3, № 3. С. 32-43.
- Tashlinskii, A.G. Computational expenditure reduction in pseudo-gradient image parameter estimation//Lecture Notes in Computer Science. 2003. Vol. 2658. P. 456-462.
- Ташлинский, А.Г. Возможности сокращения вычислительных затрат при вероятностном моделировании процесса псевдоградиентного измерения параметров изображений/А.Г. Ташлинский, М.Ю. Самойлов, А.В. Кочкадаев//Вестник Ульяновского государственного технического университета. 2005. № 1 (29). С. 52-53.
- Ташлинский, А.Г. Методика анализа погрешности псевдоградиентного измерения параметров многомерных процессов/А.Г. Ташлинский, В.О. Тихонов//Известия вузов. Радиоэлектроника. 2001. Т. 44, № 9. С. 75-80.
- Ташлинский, А.Г. Методика анализа точности псевдоградиентного оценивания геометрических деформаций последовательности изображений/А.Г. Ташлинский, Г.Л. Минкина, Г.В. Дикарина, В.И. Синицын//Наукоемкие технологии. 2007. Т. 8, № 9. С. 14-23.


