Вероятностная модель клеточных преобразований при регенерации костной ткани
Автор: Митрофанов А.В., Маслов Л.Б., Мизонов В.Е.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 1 (91) т.25, 2021 года.
Бесплатный доступ
В последнее время возрос интерес к моделированию биохимических явлений, сопровождающих регенерацию костной ткани. К этим явлениям относят диффузию, пролиферацию, дифференциацию и апоптоз основных типов клеток. Традиционно в рассматриваемый набор клеток включают четыре их типа (мезенхимальные стволовые клетки, фибробласты, хондроциты и остеобласты). При этом пространство повреждения рассматривается как «клеточный бассейн», в котором все указанные элементы одновременно существуют. В соответствии с таким подходом процессы в «клеточном бассейне» могут быть описаны системой четырех дифференциальных уравнений с соответствующими граничными и начальными условиями. Однако параметры процесса, включающие диффузию, пролиферацию, дифференциацию и апоптоз основных типов клеток, не могут быть описаны детерминированно, и, следовательно, необходимы те или иные упрощения. По этой причине различные математические инструменты привлекаются для численного решения уравнений. В настоящей работе для моделирования процесса клеточных преобразований впервые используется стохастический подход, основанный на теории цепей Маркова. Метод предполагает декомпозицию исследуемого пространства на ячейки малого конечного размера, а изменение состояния процесса рассматривается в дискретные моменты времени. В рамках принятой одномерной модели зона повреждения кости рассматривается как цилиндр с постоянным поперечным сечением. Численная реализация позволяет получить достаточно полное описание изменений пространственно-временных характеристик «клеточного бассейна» на основе начального распределения клеток. Идентификация параметров модели выполнена с использованием заимствованных из литературных источников экспериментальных данных.
Костная ткань, клетки, диффузия, дифференциация, регенерация, математическое моделирование
Короткий адрес: https://sciup.org/146282192
IDR: 146282192 | УДК: 616.314-08 | DOI: 10.15593/RZhBiomeh/2021.1.04
Текст научной статьи Вероятностная модель клеточных преобразований при регенерации костной ткани
Биологические процессы, которые реализуются при репаративном остеогенезе, сложны и многокомпонентны. Кинетика их протекания определяется как местными реактивными изменениями в области перелома, так и системными функциональными характеристиками организма в целом [4, 11, 12]. Однако сложность описания и тем более прогнозирования остеосинтеза состоит не только в том, что недостаточно © Митрофанов А.В., Маслов Л.Б., Мизонов В.Е., 2021 Митрофанов Андрей Васильевич, д.т.н., профессор кафедры прикладной математики, Иваново Маслов Леонид Борисович, д.ф.-м.н., заведующий кафедрой теоретической и прикладной механики, Иваново; в.н.с. центра национальной технологической инициативы Института передовых производственных технологий, Санкт-Петербург
Мизонов Вадим Евгеньевич, д.т.н., профессор кафедры прикладной математики, Иваново изучены местные и системные факторы, влияющие на процесс. В значительной мере сложности связаны с тем, что остеосинтез развивается одновременно в пространстве и во времени, поэтому для адекватного его формализованного представления нельзя ограничиться рассмотрением локальной (точечной) области, предполагая, что процессы во всех точках области остеогенеза протекают одинаково.
Несомненно, динамику системы можно описывать только во времени, что часто делается, например, при клинических исследованиях значимости влияния различных факторов на репаративный процесс [3, 14]. Такие исследования, безусловно, важны для накопления банка данных параметров процесса заживления, в то же время их статистическая обработка позволяет судить только о качественном уровне происходящих процессов, а переход к прогнозированию на таком феноменологическом уровне остается сомнительным. В результате подобные клинические исследования могут рассматриваться как основа описательной и феноменологической науки.
Вместе с тем в медико-биологической науке широк фронт исследований, в которых строятся достаточно детализированные математические модели изменения временных и пространственных параметров репаративного процесса [5, 11, 12, 21, 23]. Несмотря на то, что детализация значительно увеличивает количество материальных констант, которые необходимо задать для получения количественно правдоподобного результата, современный механобиологический подход позволяет проводить всесторонний теоретический анализ процессов регенерации ткани в различных условиях. Подобные модели, детализируя микроструктурные преобразования в области перелома, вносят значительный вклад в решение проблемы выбора подходящих математических инструментов для адекватного описания и прогнозирования.
Структурная перестройка неразвитой мягкой субстанции в плотную костную ткань происходит в результате дифференциации костных клеток, например, во время восстановления целостности кости после перелома и вживления скелетных имплантатов в твердое вещество костной ткани, что приводит к запуску процесса репаративной регенерации кости в зоне соприкосновения с поверхностью инородного предмета [15, 21] или между костными отломками [16]. Восстановление физикомеханических свойств костной ткани после перелома или в области имплантата обусловлено законами преобразования клеток и действием внешней механической нагрузки. Для создания адекватной математической модели регенерации кости необходимо формализовать клеточные процессы миграции, пролиферации и дифференциации основных фенотипов клеток: мезенхемальных стволовых, фибробластов, хондроцитов и остеобластов, а также временного и пространственного распределения фиброзной, хрящевой и костной тканей, создаваемых соответствующими клетками.
Теме моделирования процесса восстановления кости посвящены многочисленные работы. Особое внимание в таких работах уделяется исследованию отношений между механической стимуляцией и преобразованием клеток и клеточных структур в процессе регенерации кости. Наиболее полноценной и адекватной для достижения целей управления механической стимуляцией процессов заживления костных тканей авторы считают модель, впервые предложенную в [11]. Теоретическое исследование восстановления механических свойств ткани в зоне перелома с использованием осесимметричной конечно-элементной модели фрагмента кости было проведено с помощью уравнения диффузии, описывающего пространственновременное распределение концентрации мезенхимальных стволовых клеток.
В работе [11] указывается на необходимость исследовать процессы миграции, пролиферации и дифференциации клеток различных типов. Предложенная в [11] модель была разработана для описания изменения концентраций фибробластов, хондроцитов и остеобластов, а также временного и пространственного распределения фиброзной (соединительной), хрящевой и костной тканей. Деятельность четырех типов клеток: мезенхимальных стволовых клеток, фибробластов, хондроцитов и остеобластов, взаимодействующих в зависимости от механической стимуляции, характеризовалась преобразованием друг в друга и в структуры тканей.
Можно сказать, что пространственно-временное моделирование клеточных процессов, происходящих при восстановлении костной ткани, представляет собой научную проблему, обусловленную отсутствием разработанной методологии построения математических моделей клеточных преобразований при репаративном остеосинтезе. Частично известные трудности связаны с вопросом обоснования размера представительного объема моделируемого объекта. Если для механики однородных сред этот вопрос можно считать в известной степени решенным, то для процессов с гетерогенными неоднородными, в частности, пороупругими средами вопрос о приемлемом с теоретической и практической точек зрения уровне декомпозиции моделируемого объекта является существенным [6, 17, 19].
Целью настоящего исследования является продуктивное использование математического аппарата теории цепей Маркова для пространственно-временного моделирования процесса репаративного остеосинтеза. В конкретные задачи работы входит построение одномерной математической модели миграции клеточных элементов в области повреждения, формирования тканевых структур, идентификация основных параметров этой модели (по литературным источникам), проверка прогнозирующих возможностей модели путем сравнения расчетных данных с данными независимых экспериментов.
Формализованное представление процесса в локальном объеме и основные ЕГО ПАРАМЕТРЫ
Спектр научных исследований восстановления характеристик тканей в зоне перелома весьма широк, достаточно подробный обзор современного состояния вопроса, на наш взгляд, представлен в работах [1, 11, 12, 21]. Здесь мы не ставим цели более или менее всестороннего анализа всех процессов, которые могут быть учтены при моделировании, ограничиваясь только теми, что будут непосредственно использоваться нами при построении модели.
Построение вероятностной модели остеосинтеза должно отталкиваться от физико-химических представлений биологических процессов, обусловливающих остеосинтез, а также от математического их представления. Традиционно процесс репаративного остеосинтеза описывается системой из семи дифференциальных уравнений типа реакция–диффузия. Число уравнений соответствует числу клеточных компонентов, участвующих в остеосинтезе [1, 11, 12, 21]. Также принято считать, что пространство, где происходит остеосинтез, можно рассматривать в виде некоторого «клеточного бассейна» ( cell pool [21]), в котором одновременно существуют семь типов клеточных структур. К ним относятся четыре типа клеток: мезенхимальные стволовые клетки, фибробласты, хондроциты и остеобласты. В зависимости от ряда не вполне изученных факторов формируются три типа тканей: фиброзная (соединительная), хрящевая и костная.
С точки зрения построения модели «клеточный бассейн» представляет собой неравновесную пространственно-временную систему, описание которой включает разработку локальной схемы эволюции компонентов и установление связей, существующих между отдельными представительными объемами пространства. Процессы в локальных объемах включают: катаболизм тканевых структур, миграции клеток «бассейна», их дифференцировку и пролиферацию, апоптоз клеточных элементов, перестройку первичного костного регенерата [1, 11, 12, 21]. Формирующиеся тканевые структуры не меняют своего пространственного положения, а скорость их формирования зависит от присутствия указанных выше клеточных элементов, а также механических стимулов. Присутствие клеточных элементов в зоне формирования тканевых структур определяется комплексом процессов, включающим миграции клеточных элементов, а также их дифференциацию и апоптоз [1, 11, 12].
Способность клеточных элементов к миграции оценивается в моделях остеосинтеза не вполне однозначно. В основном принято считать, что хондроциты обладают пренебрежимо малой активностью перемещений [11, 12]. Остеобласты, как правило, рассматриваются в моделях процесса репаративного остеосинтеза как подвижные элементы, которые (согласно исследованиям [13, 21]) особенно активно распространяются вдоль поверхностей кальцинированных структур. При моделировании большинство авторов (например, [1, 11, 12]) представляют их миграции в терминах диффузии. Однако в некоторых моделях (например, [21]) остеобласты считаются неподвижными, соответственно, в зоне роста тканевых структур их присутствие объясняется только дифференциацией из других клеточных элементов. Мезенхимальные стволовые клетки и фибробласты в моделях традиционно рассматриваются как элементы, способные к активным миграциям [11, 12, 21]. Принятая схема локальной модели клеточных преобразований показана на рис. 1.
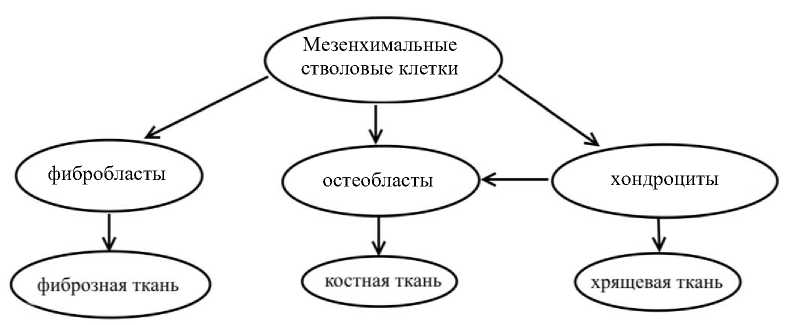
Рис. 1. Схема локальной модели клеточных преобразований при остеосинтезе
Метод исследования
В настоящей работе процессы в локальных объемах области регенерации костной ткани рассматриваются в соответствии со схемой, представленной на рис. 1, при этом формальные связи между соседними локальными объемами («ячейками») вводятся на базе математического аппарата теории цепей Маркова, который достаточно широко используется в прикладных исследованиях [10, 18–20]. При построении дискретной модели пространство области репаративного процесса подлежит декомпозиции на локальные объемы – ячейки малого, но конечного размера. Модельные представления схематично проиллюстрированы на рис. 2 и относятся к случаю цепей с конечным числом состояний и дискретным временем. Предлагаемая модель является одномерной, и в ее рамках зона повреждения кости рассматривается как набор из n цилиндров с постоянным поперечным сечением, однако при описании формальных связей между ячейками (см. рис. 2) последние изображаются условно – без учета реальной геометрии (равными кубами).
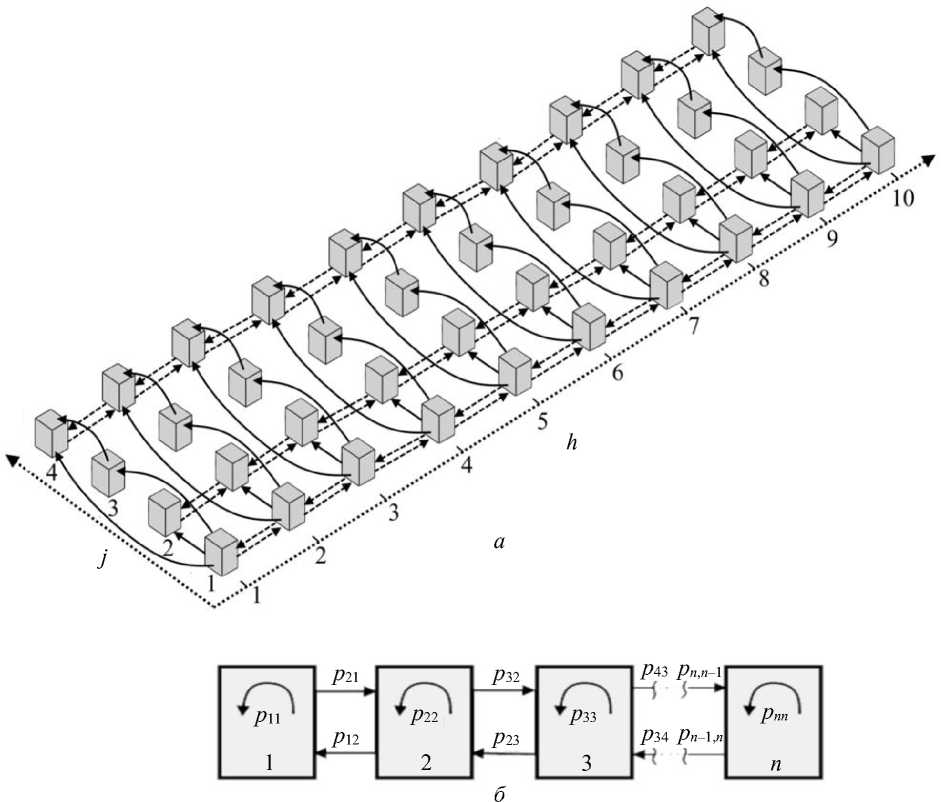
Рис. 2. К описанию расчетной схемы модели: а – ячеечная модель эволюции клеточных элементов; б – расчетная схема миграции клеточных элементов вдоль цепи ячеек
Состояние процесса в любой рассматриваемый момент времени представляется набором его характеристик, организованных в вектор-столбец (матрица 1× n ). В результате протекания случайных по своей природе клеточных преобразований рассматриваемая система (и вектор-столбец) претерпевает изменения, которые фиксируются в дискретные моменты времени t k = ( k – 1) Δ t , где Δ t – продолжительность временного перехода; k = 1, 2, ... , N – номер временного перехода (целочисленный аналог времени процесса) [18–20].
В предлагаемой модели вводятся векторы состояния не для всего ансамбля клеточных элементов, а отдельно для каждого их типа. Соответственно, несмотря на то что область повреждения кости в пространственном отношении разделена на n элементарных объемов («ячеек»), каждая ячейка характеризуется содержанием в ней четырех типов клеточных элементов, и в рассмотрение вводятся четыре вектора состояния (каждый с размерностью 1×n). На схемах удобней изображать каждый вектор состояния в виде отдельного набора ячеек, а возможные связи – в виде стрелок. Так, на рис. 2, а отдельно представлены наборы ячеек, характеризуемые соответствующими векторами состояния Sj, каждый из которых позволяет представить распределение в пространстве репаративного процесса соответствующих клеточных элементов: j = 1 – мезенхимальных стволовых клеток; j = 2 – фибробластов, j = 3 – хондроцитов; j = 4 – остеобластов. Как видно из рис. 2, а, дифференциация клеток (показана стрелками со сплошным начертанием) рассматривается в модели как «поперечный» перенос между соответственными ячейками параллельных цепей. При этом из S1 возможен перенос в любые другие цепи ячеек (S2, S3 и S4), что полностью соответствует возможным вариантам дифференциации мезенхимальных стволовых клеток (см. рис. 1). Также возможным является преобразование хондроцитов в остеобласты (допускается перенос из S3 в S4).
Продольный перенос клеточных компонентов в осевом направлении области репаративного процесса рассматривается как явление диффузии клеточных элементов в направлении соответствующих цепей (показано стрелками с пунктирным начертанием) и описывается на основе математического аппарата теории цепей Маркова. Состояние любой цепи можно считать описанным, если на каждом шаге будет задано распределение вероятностей на пространстве исходов, определяющее состояния, в которые может перейти система в результате следующего шага. Переходные вероятности принято записывать в так называемую матрицу переходных вероятностей (переходную матрицу) [10, 18–20]. При таком (матричном) способе исследования, каждый последующий вектор состояния получается путем умножения переходной матрицы на текущий вектор состояния. В дополнение к указанной рекуррентной процедуре к вектору состояния прибавляются источниковые и стоковые слагаемые, позволяющие описать гибель (апоптоз) и порождение (пролиферацию) клеток в ячейках цепи.
Построение вероятностной модели остеосинтеза в конечном счете должно отталкиваться от физико-химических представлений биологических процессов, входящих в состав остеосинтеза, а также от математического их представления. Традиционно процесс остеосинтеза описывается системой из семи дифференциальных уравнений типа реакция–диффузия. Число уравнений соответствует числу клеточных компонентов, участвующих в остеосинтезе.
Если принять допущение, что для описания остеосинтеза достаточно наблюдать за присутствием в области заживления четырех типов элементов, то расчетная схема при математической формализации включает в себя четыре совместно решаемые дифференциальные уравнения [1, 11, 12, 21], которые описывают эволюцию клеточных элементов и записываются в общем виде как д c.
= Di д t j
д 2 c дx2
+ ffc,
1 -
„ A c j max cj )
- rap e. ±У f , c.
^ j j ^^ i ^ j ^ i i
1 -
c j max
Cj )
,
где j = 1 (мезенхимальные стволовые клетки); j = 2 (фибробласты); j = 3 (хондроциты); j = 4 (остеобласты); t – время процесса; с j – нормальная концентрация клеток j -го типа; с j max – максимальная концентрация клеток j -го типа; D j – коэффициент диффузии для j -го клеточного элемента; f jpr – коэффициент, определяющий интенсивность пролиферации клеток j -го типа; f jар – коэффициент, определяющий интенсивность гибели клеток j -го типа; f ijD – параметр, определяющий интенсивность дифференциации i -го типа клеток в j -й.
При переходе к ячеечным цепным моделям на основе теории цепей Маркова уравнение вида (1) заменяется рекуррентным матричным соотношением вида
S k + 1
= P7 k • S k + f/r • S k .* 1
max
• S k A t - f ap • S k A t + F, D , j jj j
где P – матрица переходных вероятностей, которая является основным оператором модели; F D – вектор источников и стоков, связанных с процессами дифференциации;
S jk – вектор, соответствующий текущему значению концентрации клеточных элементов j -го типа; S j max – допустимое количество клеток j -го типа в ячейке, соответствующее максимально возможной их концентрации с j max; символ «.*» означает поэлементное выполнение математических операций.
Здесь важно отметить, что уравнения вида (1) традиционно записывают через концентрации элементов, а в моделях, построенных на основе теории цепей Маркова, принято оперировать аддитивными переменными (в данном случае – количеством клеточных элементов в ячейках). Таким образом, решением (1) является функция распределения концентрации частиц, а решением (2) является распределение числа клеточных элементов по ячейкам. Так как при решении задач исследования предполагается, что представительный объем V (размеры ячейки) системы «клеточный бассейн» не изменяется в течение всего времени наблюдения, то переход от концентраций к аддитивным характеристикам (количеству клеточных элементов) в любой момент времени выполняется через соотношение S j = c j · V .
Если объект (пространство «клеточного бассейна») представлен как набор из конечного числа (1, 2, ..., n ) ячеек (представительных объемов малого, но конечного размера), то переходная матрица будет иметь размерность n × n и следующий вид (направления возможных переходов проиллюстрированы рис. 2, б ):
При математической формализации регенеративного процесса через уравнение (2) матрица P берет на себя функцию «перемешивающего» фактора и отвечает за все диффузионные процессы в системе, остальные слагаемые являются источниковыми или стоковыми. В соответствии с этим переходные вероятности будут связаны с размерными коэффициентами диффузии j -го компонента D j через соотношения вида
D - A t d =
,
J Ax x где Δt – продолжительность одного рекуррентного перехода для (2); Δx – размер ячейки.
Переходная матрица P в общем случае может и не содержать нулевых элементов [10, 19]. Однако в настоящей работе предполагается, что за время Δ t одного рекуррентного перехода клеточный элемент не может переместиться далее соседней ячейки, поэтому переходная матрица является трехдиагональной (на главной диагонали ее содержатся вероятности остаться в наблюдаемой ячейке, а на диагоналях под и над главной – вероятности миграций в соседнюю ячейку вперед и назад соответственно) и имеет следующий вид:
|
"1 - d |
d . |
.. 0 " |
|
|
d |
1 - 2 d,. |
.. 0 |
|
|
P = |
0 |
d . |
.. 0 |
|
0 |
0. |
.. 1 — dj |
Источниковые и стоковые слагаемые в уравнениях (1)–(2) формируются обычным для моделей [11, 12, 21] образом. Так, слагаемые, отвечающие за дифференциацию клеток, рассчитываются особым образом для каждого типа клеточных элементов [11, 12]:
j = 1 (мезенхимальные стволовые клетки):
Г ,7 Г ,7 „,<1,7
F D = - f D . s k .* 1-- —. S k a t - f D . S k .* 1-- —. S k a t - f D . S k .* 1--— S k A t ; (6)
1 1 1 max 2 1 1 max 3 1 1max 4
V ° 2 7 V 3 3 7 V ° 4
j = 2 (фибробласты):
r
FD = fD . S,k .* 1---Sk At;(7)
2 1 1 max2
-
V ° 2
j = 3 (хондроциты):
riar
FD = f D . Sk .* 1--Sk At - fD . Sk .* 1--Sk At;(8)
3 1 1 max 3 3 3max 4
V ° 3 7 V ° 4
j = 4 (остеобласты):
r ,7r
FD = f D .Sk.* 1Sk At + fD .Sk.* 1Sk At.(9)
4 1 1 max 4 3 3 max4
V ° 4 7 V ° 4
Использование основного модельного уравнения (2) и совместно с независимыми от него соотношениями (6)–(9) и эмпирическими параметрами, позволяет экстраполировать пространственно-временные характеристики клеточных элементов на время Δ t рекуррентного шага. Эволюция состояния системы, таким образом, наблюдается в дискретные моменты времени t k = ( k – 1)Δ t , где Δ t – промежуток времени между соседними фиксируемыми состояниями системы (шаг по времени); k – номер временного рекуррентного шага.
Сформулированная математическая модель, основанная на соотношениях (2)–(9), принципиально не зависит от материальных констант (хотя их значения, естественно, определяют прогностические возможности модели), т.е. разрабатываемая модель не является следствием эмпирических данных, что позволяет рассматривать ее в качестве достоверной научной основы для расчета и прогнозирования протекания репаративного процесса регенерации костной ткани при условии, что прогностические возможности модели будут в известной мере обоснованы. Указанное обоснование требует по крайней мере проверки того, что получаемые при помощи предложенной модели решения хотя бы в качественном отношении не противоречат известным результатам и априорным знаниям о процессе.
Результаты численного моделирования
Предложенная в настоящей работе математическая модель, дополненная заимствованными эмпирическими коэффициентами, потенциально должна позволять прогнозировать распределение клеточных элементов в зоне репаративного остеосинтеза. В то же время качество прогноза, очевидно, будет зависеть и от качества банка данных материальных констант процесса. Поэтому на данном этапе представляется более целесообразным качественный анализ получаемых численных решений, начиная с наиболее простых сценариев процесса.
Так, в работе [5] показано, что пространственно-временное распределение концентрации активных клеток в зоне репарации может быть аппроксимировано зависимостью, полученной разложением функции с1max в ряд Фурье. При условии, что коэффициент диффузии клеток D1 не зависит от времени и концентрации клеточных элементов, данная зависимость может быть представлена как
, С max_ 4c ™ax V ( - 1) ' — 1 С OS f (2 1 — IL X ln f _ Г) (2 1 — 1) 2 П " ^ )
C 1 ( x , t ) c l c l / , cos I I exp D 1 2 . (10)
П i = 1 21 —1 у 21 у ^ 4 1 ^
Поскольку на окончательный результат влияют не абсолютные значения концентрации клеток, а относительные, то получаемые результаты удобно представить в виде зависимости c 1 ( x , t )/ c 1 max [5]. Предлагаемая математическая модель, основанная на рекуррентном соотношении (2), должна, очевидно, давать близкие результаты, если принять равными нулю материальные константы, определяющие пролиферацию, дифференциацию и апоптоз клеток (т.е. f 1 pr = 0; f 1 D = 0; f 1 ap = 0). На рис. 3 представлены расчетные распределения относительной концентрации клеток c 1 ( x , t )/ c 1 max в области длиной 10 мм, рассчитанные по формуле (10) при различных значениях коэффициента диффузии и в различные моменты времени (показаны маркерами), а также соответствующие распределения, полученные по предлагаемой в настоящем исследовании модели (показаны линиями). Как видно, наблюдается хорошее совпадение расчетных данных, полученных по зависимости (2) и по предлагаемой модели, что подтверждает работоспособность предлагаемой математической модели, по крайней мере для описания диффузионного переноса клеточных элементов.
Для рассмотрения с помощью предлагаемой в настоящей работе модели других сценарных вариантов развития процессов в указанной области требуется идентификация ее параметров. Параметры модели (значения коэффициентов диффузии, скоростей процессов дифференциации, пролиферации и апоптоза клеток и соответствующих тканей, максимальные значения концентраций клеток и тканей), полученные на основе анализа реферативных данных [12, 21], представлены в таблице.
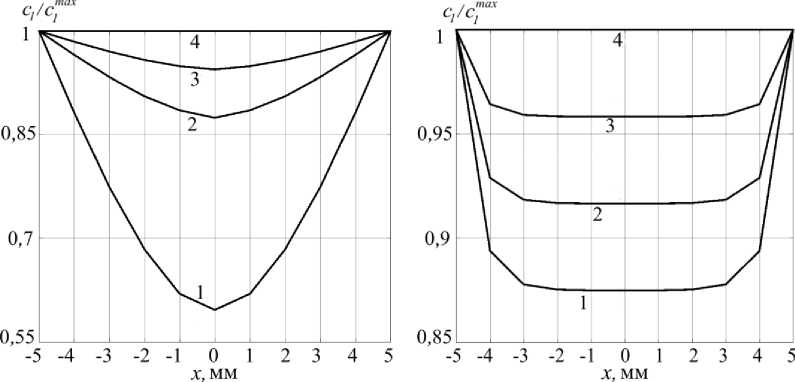
Следующим вариантом развития процесса в указанной области длиной 10 мм был сценарий, когда на процесс диффузии клеточных элементов накладывается их пролиферация, соответственно f 1 pr ≠ 0, а остальные материальные константы по-прежнему принимаются равными нулю ( f 1 D = 0 и f 1 ap = 0). На рис. 4, а представлены результаты численных экспериментов влияния, характеризующих влияние величины коэффициента f 1 pr на распределение относительной концентрации активных клеток вдоль продольной оси x зоны репарации в конечный момент времени t = 120 сут (дней) при D 1 =0,1 мм2/день. Для большей наглядности на рис. 4, а приведено также распределение, полученное для случая чистой диффузии (при D 1 = 0,1 мм2/день и f 1 pr = 0; f 1 D = 0; f 1 ap = 0). Как видно из рис. 4, а , результаты в качественном отношении являются достаточно ожидаемыми: так как численный эксперимент не предполагает гибели клеток или дифференциации, то введение в рассмотрение пролиферации значительно интенсифицирует процесс накопления активных клеток в области
Параметры модели движения клеточных элементов
|
Тип элемента |
c max , мм –2 |
f pr , мин–1 |
D , мкм2/мин |
f D , мин–1 |
f ap , мин–1 |
|
Мезенхимальные стволовые клетки |
106 |
4,1667·10–4 |
0,06 |
2,0833·10–4 |
3,4722·10–5 |
|
Фибробласты |
108 |
1,3889·10–4 |
0,04 |
— |
3,4722·10–5 |
|
Хондроциты |
2·105 |
1,3889·10–4 |
6,9444·10–5 |
6,9444·10–5 |
|
|
Остеобласты |
2,7·104 |
2,0833·10–4 |
0,01 |
– |
1,0417·10–4 |
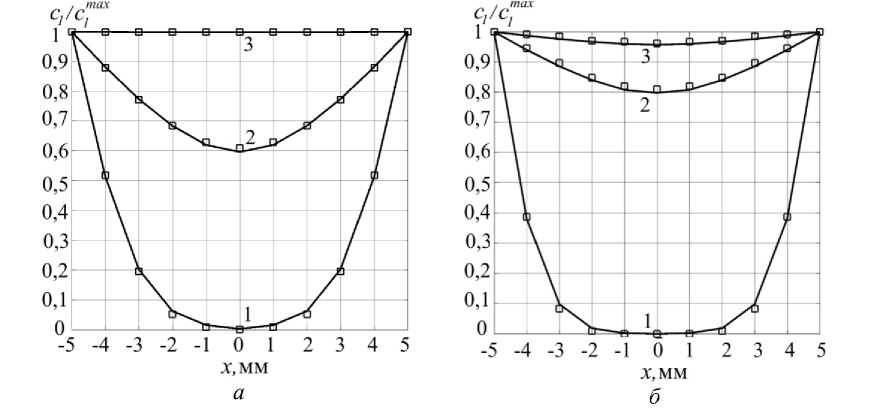
Рис. 3. Распределение относительной концентрации активных клеток вдоль продольной оси x зоны репарации: а – в конечный момент времени t = 120 сут (дней) при различных значениях коэффициента диффузии: 1 – при D 1 = 0,01 мм2/день; 2 – при D 1 = 0,1 мм2/день; 3 – при D 1 = 0,67 мм2/день; б – в различные моменты времени при фиксированном значении коэффициента диффузии D 1 = 0,67 мм2/день: 1 – к моменту времени t = 1 день; 2 – к моменту времени t = 30 дней; 3 – к моменту времени t = 60 дней
а б
Рис. 4. Распределение относительной концентрации активных клеток вдоль продольной оси x зоны репарации: а – в конечный момент времени t = 120 сут (дней) при фиксированном значении коэффициента диффузии
D1 = 0,1 мм2/день: 1 – при f1pr = 0; 2 – при f1pr = 2,0833·10–3; 3 – при f1pr = 1,3889·10–3; 4 – при f1pr= 4,1667·10–4; б – в конечный момент времени t = 120 сут (дней) при прификсированных значениях D1= 0,1 мм2/день и f1pr = 4,1667·10–4: 1 – при f1ap = 6,9444·10–5; 2 – при f1ap = 3,4722·10–5 (табличное значение); 3 – при f1ap = 1,7361·10–5; 4 – при f1ap = 0
репарации. Это тем более очевидно, что значение коэффициента было принято в 20 раз меньше табличного ( f 1 pr = 2,0833·10–3) и в 30 раз меньше табличного ( f 1 pr = 1,3889·10–3), так как при табличном значении ( f 1 pr = 4,1667·10–4) во всей области достигается максимально возможная концентрация стволовых клеток.
Необходимо отметить, что включение в рассмотрение пролиферации без процесса гибели клеток, очевидно, не вполне корректно не только с биологической точки зрения, но и с точки зрения модельных представлений. Включение в численный анализ процесса апоптоза ( f 1 ap ≠ 0) позволяет сразу вернуться к табличным значениям материальных констант для получения качественно-непротиворечивых результатов. Анализ этого сценария представлен на рис. 4, б : чем более интенсивна гибель клеток, тем к заданному моменту времени меньше активных клеток наблюдается в любом локальном объеме.
Введение в численный эксперимент процесса дифференциации ( f 1 D ≠ 0) также приводит к получению качественно-непротиворечивого результата (рис. 5, а ). Результаты, представленные на рис 5, а , получены при использовании табличных значений других материальных констант, определяющих процесс ( f 1 ap = 3,4722·10–5; f 1 pr = 4,1667·10–4), и коэффициента диффузии D 1 = 0,1 мм2/день, а также введении дифференциации стволовых клеток ( f 1 D ≠ 0). В общем случае концентрация активных клеток уменьшается по сравнению со случаем, когда f 1 D = 0 (этот случай также приведен на рис. 5, а – линия 4 ), так как дифференциация подразумевает «затраты» этих клеток на производство других клеток. Соответственно, уменьшение или увеличение коэффициента f 1 D приводит к повышению или снижению концентрации оставшихся активных клеток.
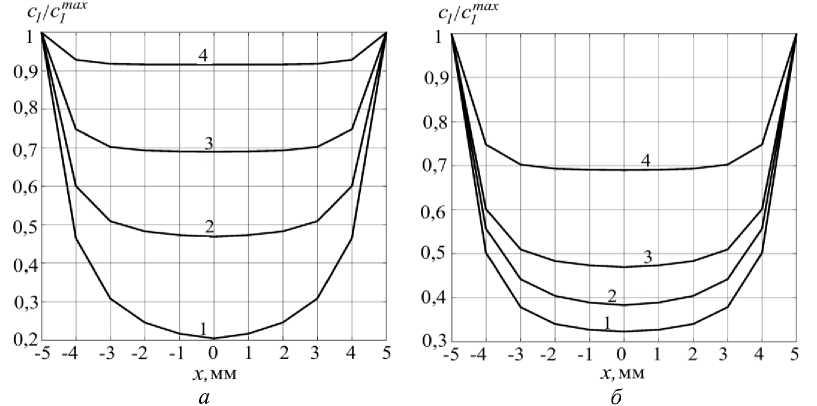
Рис. 5. Распределение относительной концентрации активных клеток вдоль продольной оси x зоны репарации при фиксированных значениях следующих параметров: D 1 = 0,1 мм2/день, f 1 pr = 4,1667·10-4, f 1 ap = 3,4722·10–5: а – в конечный момент времени t = 120 сут (дней): 1 – при f 1 D = 3,1250·10–4; 2 – при f 1 D = 2,0833·10–4; 3 – при f 1 D = 1,0417·10–4; 4 – при f 1 D = 0; б – в конечный момент времени t = 120 сут (дней): 1 – при f 1 D = 2,0833·10–4; f 3 D = 6,9444·10–5 и f 2 ap = 3,4722·10–5, f 3 ap = 6,9444·10–5, f 4 ap = 1,0417·10–4; 2 – при f 3 D = 6,9444·10–5 и f 3 ap = 6,9444·10–5, но при отсутствии гибели других клеток ( f 2 ap = 0; f 4 ap = 0); 3 – при f 3 D = 6,9444·10–5 и отсутствии гибели других клеток ( f 2 ap = 0; f 3 ap = 0, f 4 ap = 0);
4 – при f 3 D = 0 и отсутствии апоптоза других клеток ( f 2 ap = 0; f 3 ap = 0, f 4 ap = 0)
Заметный эффект на профиль распределения активных клеток оказывают не только значения материальных констант, непосредственно связанных с миграцией, дифференциацией, гибелью и пролиферацией стволовых клеток. На рис. 5, б показано влияние на указанный профиль факторов, которые определяют интенсивность дифференциации хондроцитов (линия 3 на рис. 5, б), дифференциации и гибели хондроцитов (линия 2 на рис. 5, б), а также дифференциации хондроцитов при включении в рассмотрение апоптоза всех клеточных элементов (линия 1 на рис. 5, б).
Результаты численных экспериментов, показанные на рис. 3, 4, представляют собой, по существу, попытку анализа изолированных процессов (диффузии, пролиферации, дифференциации и т.д.), что интересно с точки зрения функционирования модели. В то же время указанные результаты достаточно очевидно обнаруживают, что экспериментально установленные материальные константы процессов позволяют получать правдоподобные распределения только в сочетании друг с другом, в противном случае результаты получаются качественно противоречивыми. На рис. 5 приводятся результаты моделирования, когда протекание процессов уже рассматривается относительно комплексно (распределение стволовых клеток при наибольшем числе процессов, включенных в модель, представлено на рис. 5, б , линией 1 ), однако в то же время не приведены соответствующие этому сценарию распределения других клеток (фибробластов, остеобластов и хондроцитов). Соответствующие относительные распределения представлены на рис. 6, а .
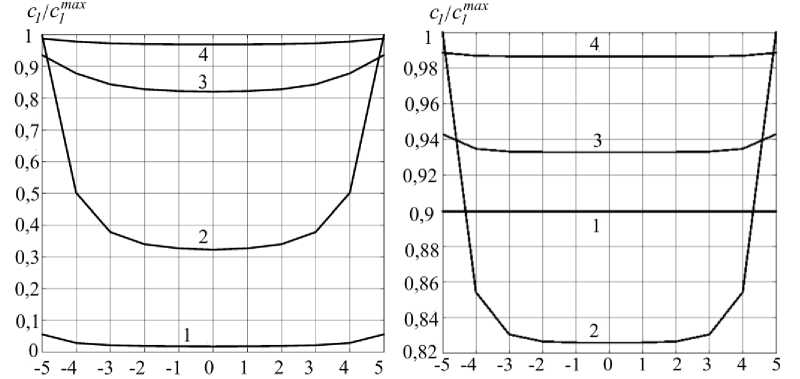
.X, MM X, мм а б
Рис. 6. Распределение относительной концентрации различных клеточных элементов в конечный момент времени t = 120 сут (дней) вдоль продольной оси x зоны репарации при фиксированных ненулевых значениях следующих параметров: а – при D 1 = 0,1 мм2/день, f 1 pr = 4,1667·10–4, f 1 D = 2,0833·10–4; f 3 D = 6,9444·10–5 и f 1 ap = 3,4722·10–5, f 2 ap = 3,4722·10–5, f 3 ap = 6,9444·10–5, f 4 ap = 1,0417·10–4 ( 1 – фибробласты, 2 – стволовые клетки, 3 – хондроциты, 4 – остеобласты); б – при табличных значениях (таблица) всех переменных ( 1 – фибробласты, 2 – стволовые клетки, 3 – хондроциты, 4 – остеобласты)
Как видно (см. рис. 6, а ), относительные распределения всех клеточных элементов неравномерны в зоне репарации, относительные концентрации фибробластов, хондроцитов и остеобластов (линии 1 , 2 и 4 ) не достигают единицы, хотя и увеличиваются с ростом концентрации стволовых клеток. На рис. 6, б показаны соответствующие распределения, но для случая, когда в рассмотрение включены все процессы, параметры которых представлены в таблице.
Здесь обращает на себя внимание заметное увеличение концентрации фибробластов, причем распределение их концентрации близко к равномерному. Вместе с тем выросли концентрации (по сравнению со случаем, представленным на рис. 6, а) всех остальных клеточных элементов. Наблюдаемая ситуация объясняется комплексом процессов, которые начинаются с введением в рассмотрение пролиферации фибробластов (процесса, который отсутствует для случая рис. 6, а). Значение предельно допустимой концентрации и уровень пролиферации фибробластов обеспечивают быстрое повышение их концентрации, при этом снижая «затраты» стволовых клеток, концентрация которых также возрастает, что запускает ускоренную дифференциацию в другие клеточные элементы (хондроциты и остеобласты).
На рис. 7 показаны результаты численных экспериментов, характеризующие некоторые этапы переходного (в отношении результатов для момента времени t = 120 сут (см. рис. 6, б )) состояния «клеточного бассейна». Все результаты получены с использованием материальных констант, приведенных в таблице, но при D 1 = 0,1 мм2/день.
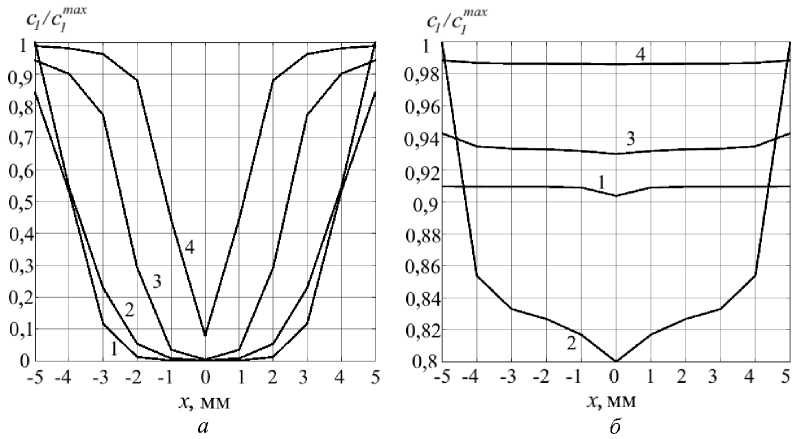
Рис. 7. Распределение относительной концентрации различных клеточных элементов вдоль продольной оси x зоны репарации при фиксированных ненулевых значениях параметров модели (таблица) и D 1 = 0,1 мм2/день ( 1 – фибробласты, 2 – стволовые клетки, 3 – хондроциты, 4 – остеобласты): а – через две недели (14 сут) после начала процесса; б – через семь недель (42 сут) после начала процесса
На рис. 7, а представлены расчетные распределения клеточных элементов для момента времени (14 сут), когда на краях наблюдаемой области уже образовалось некоторое заметное количество различных клеточных элементов. Однако в середине области наблюдается заметный дефицит стволовых клеток, который объясняется тем, что в процессе миграции от краев они были израсходованы в результате дифференциации (т.е. процессы пролиферации и диффузии к этому моменту времени еще не обеспечили значимой концентрации активных клеток в центральной части повреждения). На рис. 7, б показано изменение этой ситуации со временем: концентрация стволовых клеток в середине наблюдаемой области ощутимо ниже, чем у других клеточных элементов, что говорит о сравнительно высоком уровне дифференциации. В то же время за счет миграции и пролиферации стволовых клеток обеспечена достаточно высокая их концентрация даже в центральной части области репарации.
Обсуждение
Предложенная в настоящей работе математическая модель, дополненная эмпирическими коэффициентами, заимствованными из литературных источников, позволяет получать непротиворечивые в качественном отношении результаты, что в конечном счете позволяет рассматривать ее как достоверную основу для создания компьютерного метода расчета эволюции состояния клеточных элементов в зоне репаративного остеосинтеза.
В то же время достоверность результатов прогноза, очевидно, достижима только при включении в рассмотрение достаточно большого количества основных элементарных процессов, составляющих остеосинтез. Последнее говорит о том, что упрощение модельных представлений, очевидно, не является целесообразным. Вместе с тем разрабатываемая модель на данном этапе ее формирования имеет некоторые ограничения, связанные с отсутствием в ней ряда значимых для остеогенеза факторов, включение которых в рассмотрение составляет перспективу развития предложенной стратегии моделирования. В частности, известно, что наряду с механическим раздражением сращиваемого участка костной мозоли общеукрепляющей физико- и медикаментозной терапией признаются и другие факторы биологического, физического и химического воздействия – нуклеиновые кислоты, гормоны, электрическое и магнитное поле, ультразвук, баротерапия, кроме того оправдывает себя как стимулирующий фактор и костная пластика [3, 4, 11, 12]. Имеют существенное значение поражающий фактор, вызывающий разрушение всех основных структур кости с формированием гематомы между отломками, характер кровоснабжения пораженного участка, формирующий гематому, которая инициирует каскад биологических реакций, направленных на увеличение проницаемости сосудов и увеличение концентрации медиаторов воспаления и цинокинов [1, 5, 9, 11]. Указанные факторы не учитываются на данном этапе построения модели, поэтому вполне ожидаемо, что это лимитирует ее прогностические возможности. Вместе с тем во многих исследованиях [7, 20] отмечается, что формальное увеличение количества параметров уравнений (материальных констант процесса) может и отрицательно сказываться на прогностической эффективности модели.
Кроме того, разработанная модель является одномерной, однако известно, что физико-механические свойства костной ткани анизотропны и в значительной мере определяются её внутренней архитектурой [2, 8].
Заключение
В работе на основе математического аппарата теории цепей Маркова предложена ячеечная вероятностная модель, позволяющая прогнозировать пространственно-временные характеристики формирующихся распределений основных клеточных элементов при заживлении костного повреждения. Предложенная модель, дополненная известными материальными константами, позволила качественно непротиворечиво описать процессы миграции, дифференциации, гибели и пролиферации клеточных элементов в зоне регенеративного остеосинтеза. С учетом того, что набор материальных констант и данные эксперимента являются независимыми не только друг о друга, но и от разработанной модели, последнюю можно рассматривать как достоверную научную основу для компьютерного моделирования процессов регенеративного остеосинтеза.
Список литературы Вероятностная модель клеточных преобразований при регенерации костной ткани
- Кирпичев И.В., Коровин Д.И., Маслов Л.Б., Томин Н.Г. Математическая модель клеточных преобразований при регенерации костной ткани в условиях изменяющейся биохимической среды с возможной механорегуляцией // Российский журнал биомеханики. - 2016. - Т. 20, № 3. - С. 220-235.
- Киченко А.А., Тверье В.М., Няшин Ю.И., Осипенко М.А., Лохов В.А. Постановка начально-краевой задачи о перестройке трабекулярной костной ткани // Российский журнал биомеханики. - 2012. -Т. 16, № 4. - С. 36-52.
- Ключевский В.В., Самодай В.Г., Гильфанов С.И., Михайленко Б.С. Сравнительная характеристика результатов остеосинтеза медиальных переломов шейки бедренной кости в зависимости от возраста пациента, сроков с момента травмы до операции и вида фиксатора // Вестник экспериментальной и клинической хирургии. - 2010. - Т. 3, № 1. - С. 56-59.
- Корж Н.А., Дедух Н.В., Никольченко О.А. Репаративная регенерация кости: современный взгляд на проблему. Системные факторы, влияющие на заживление перелома // Ортопедия, травматология и протезирование. - 2006. - № 2. - Сообщ. 3. - С. 93-99.
- Маслов Л.Б. Математическая модель структурной перестройки костной ткани // Российский журнал биомеханики. - 2013. - Т. 17, № 2. - С. 39-63.
- Сибиряков Б.П., Прилоус Б.И. Статика, динамика и хаос между ними в структурированных средах // Физическая мезомеханика. - 2009. - Т. 12, № 1. - С. 101-106.
- Тверье В.М. Кинетические уравнения перестройки трабекулярной костной ткани в пространстве Ильюшина // Российский журнал биомеханики. - 2019. - Т. 23, № 2. - С. 293-301.
- Экспериментальные методы в биомеханике / под ред. Ю.И. Няшина, Р.М. Подгайца. - Пермь: Изд-во Перм. гос. техн. ун-та, 2008. - 400 с.
- Ababii I., Ciobanu P. Actualiatisi perspective in transplanta reacelulara // Curierul Medical. - 2005. -No. 3. - P. 42-47.
- Berthiaux H., Mizonov V., Zhukov V. Application of the theory of Markov chains to model different processes in particle technology // Powder Technology. - 2005. - Vol. 157. - P. 128-137.
- Geris L., Gerisch A., Sloten J.V., Weiner R.D., Oosterwyck H.V. Angiogenesis in bone fracture healing: a bioregulatory model // J. Theor. Biol. - 2008. - Vol. 251. - P. 137-158.
- Isaksson H., van Donkelaar C.C., Huiskes R., Ito K. A mechano-regulatory bone-healing model incorporating cell-phenotype specific activity // Journal of Theoretical Biology. - 2008. - Vol. 252. -P. 230-246.
- Kaplan R.N., Psaila, B., Lyden, D. Niche-to-niche migration of bone-marrow-derived cells // Trends Mol. Med. - 2007. - Vol. 13. - P. 72-81.
- Lu C., Miclau T., Hu D., Marcucio R.S. Ischemia leads to delayed union during fracture healing: a mouse model // Journal of Orthopaedic Research. - 2007. - Vol. 1. - P. 51-61.
- Maslov L.B. Mathematical model of bone regeneration in a porous implant // Mechanics of Composite Materials. - 2017. - Vol. 53, no. 3. - P. 399-414.
- Maslov L.B. Mathematical modeling of the callus mechanical properties restoration // J. Appl. Math. Mech. - 2015. - Vol. 79, no. 2. - P. 195-206.
- Maslov L.B. Dynamic model of a periodic medium with double porosity // Mechanics of Solids. - 2018. -Vol. 53, no. 2. - P. 184-194.
- Mitrofanov A., Mizonov V., Camelo A., Tannous K. Application of the theory of Markov chains to theoretical study of processes in a circulating fluidized bed // Particulate Science and Technology. - 2019. -Vol. 37, no. 8. - P. 1028-1033.
- Mitrofanov A., Mizonov V., Tannous K. Ovchinnikov L. A Markov chain model to describe fluidization of particles with time-varying properties // Particulate Science and Technology. - 2018. - Vol. 36, no. 2. -P. 244-253.
- Mitrofanov A., Mizonov V., Shuina E., Kasatkina N., Shpeynova N. Theoretical and experimental study of particulate solids drying in circulating fluidized bed // JP Journal of Heat and Mass Transfer. - 2019. -Vol. 18, no. 2. - P. 267-276.
- Mukheijee K., Gupta S. Mechanobiological simulations of peri-acetabular bone ingrowth: a comparative analysis of cell-phenotype specific and phenomenological algorithms // Med. Biol. Eng. Comput. - 2017. -Vol. 55, no. 3. - P.449-465.
- Stains J.P., Civitelli R. Cell-to-cell interactions in bone // Biochem. Biophys. Res. Commun. - 2005. -Vol. 328. - P. 721-727.
- Vermolen F.J., Andreykiv A., van Aken E.M., Linden J.C.., Javierre E., van Keulen A. A suite of mathematical models for bone ingrowth, bone fracture healing and intra-osseous wound healing // Advanced Computational Methods in Science and Engineering. Lecture Notes in Computational Science and Engineering. - 2009. - Vol 71. - P. 289-314.


