Вероятностная модель процесса смешивания ингредиентов комбикормов в смесителе-реакторе непрерывного действия

Математическая модель процесса смешивания полидисперсных сред должна отражать его стохастические особенности в виде неравномерности распределения элементов фаз по времени пребывания в аппарате, по размерам частиц, по неравномерности удерживающей способности аппарата, случайному характеру распределения материальных и тепловых потоков фаз по рабочему объёму, по неоднородности физико-химических свойств среды, осложнённых химической реакцией. При смешивании компонентов комбикормов имеет место экзотермическая реакция взаимодействия оксидов кальция и магния с водой, что приводит к разогреву многокомпонентной смеси, и прежде всего мелассы, и как следствие, к снижению её вязкости. С повышением температуры в мелассе происходит карамелизация сахаров и в дальнейшем превращение их в твёрдую кристаллическую массу [1, 2].

Поэтому для математического описания процесса смешивания ингредиентов комбикормов при наличии химической реакции целесообразно использовать систему дифференциальных уравнений академика В. В. Кафарова. Предложенная им гипотеза на основе теории марковских процессов «всякую многокомпонентную смесь можно рассматривать как результат итерационного процесса смешивания двух компонентов до достижения заданной однородности всех ингредиентов в смеси», что позволяет рассматривать процесс смешивания бинарной композиции в лопастном смесителе в виде дифференциальных уравнений изменения концентраций ингредиентов А и В во времени:

• ^{d (} c A m A ) = - k ⁽ c A - m A ) 2 + kD A ; (1) dt

d ⁽ cBdt mB ) = - k ( c B — m B ) 2 + kD B , (2) где k = //■( NA a + N b b ) /b'- коэффициент; с а , св – содержание ингредиентов А и В ; mА , mВ – математические ожидания содержания ингредиентов А и В , соответствующие значению в рецептуре многокомпонентной смеси; ц - эмпирический коэффициент; NA, NB – число частиц ингредиентов А и В в смеси; a ’ = a y AVA; b ' = b y BVB; a и b - число частиц, входящих в смесь ингредиентов А и В; VA и VB – объёмы частиц А и В; y A и у В - плотности частиц А и В; DA и DB – разброс случайной величины в области математического ожидания, характеризующий неоднородность смеси и необходимость дальнейшего смешивания частиц.

Уравнения (1) и (2) характеризуют изменение содержание ингредиентов А и В в рабочей камере смесителя. В производственных условиях оценка однородности смеси осуществляется по отбору определённого числа проб. Уравнение (1) при отборе n проб в произвольно выбранных точках рабочей камеры смесителя при l повторностях в каждой точке принимает вид:

^{d ( c}, ^—

m = — k ( c j

dt i = 1, 2

— m )2 + kDr cij

n ; j = 1, 2,…, l .

Для оценки качества смеси перейдём от содержания ингредиентов к выборочному разбросу случайной величины в области математического ожидания. Систему уравнений (3) просуммируем по n пробам и l повторностям и разделим на nl , тогда получим:

• -7 d 11 ( c j — m ) =— k :Ё ^L ( c , — m j ² + k^L^LO; (4) nl dt , = 1 j = 1 nl i = 1 j = 1 nl , = 1 j = 1 j

Величина в левой части уравнения (4) является осреднённой по n пробам и l повторностям содержания ингредиента А в смеси. Вследствие независимости наблюдаемых отклонений в n пробах и l повторностях двойные суммы парных произведений центрированных случайных величин являются корреляционными моментами и равны нулю. Отсюда:

nl

11 c , i = 1 j = 1

—

1 ² n l m ) = 11^{( c}-j

i = 1 j = 1

— m ) 2 = nl a 2 , ⁽⁵⁾

где ^ - выборочный разброс случайной величины в области математического ожидания ингредиента в многокомпонентной смеси.

Первое слагаемое в правой части уравнении (4) является осреднённым выборочным разбросом случайной величины в области математического ожидания ингредиента в многокомпонентной смеси, характеризующий неоднородность смеси и необходимость дальнейшего смешивания частиц, которая имеет смысл спонтанного перераспределения неоднородных частиц, обусловленного сегрегацией σс² . Тогда уравнение (4) может быть представлено следующим образом:

nld^ =— k(^2 — ^2 ) nldt                  c , где k – коэффициент, определяющий константу скорости смешивания.

Кривые кинетики процесса смешивания, характеризующие изменение выборочного разброса случайной величины в области математического ожидания представлены на рисунке 1.

И позволяют определить значение ор², при котором достигается динамическое равновесие между спонтанным перераспределением частиц при смешивании он² и сегрегацией ос² .

Уравнение (9) после интегрирования при-

нимает вид:

1 . 1+V л +1V о² ,------ln------         ----

V T + 1  1 - V T + 1 До

2 k nl

Л

+ ln C .(10)

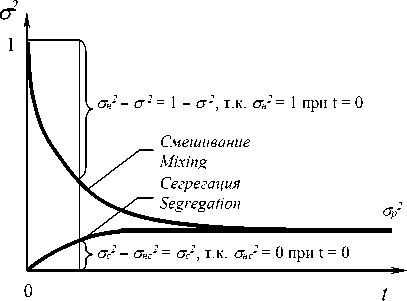
Рисунок 1. Кривые кинетики процессов смешивания и сегрегации

Постоянную интегрирования С найдём из начального условия t = 0, о² = 0:

ln C =

1 in 1+V Л +1 7 л +Г ^п 1 - 7 л +1

С учётом (11) уравнение (10) приводится

к виду:

1 , 1+V л +1V о² ,---------in --------- ,            ,------

7 л + !  1 - V T + i 4о

1   _ln1 + У л + 1

7 л +Г ⁿ 1 -V T + T

2 k nl _t

Л

или

Figure 1. Mixing and segregation kinetics curves

Пусть процессу смешивания многокомпонентных смесей соответствует график функ-ции f(о) (он' - о² ), а процессу сегрегации -график функции f(о) =(ос² - онс² ), а между ними установлена линейная связь:

о н ² - о ² = лД - о н ) ,         (6)

где он² - начальный выборочный разброс случайной величины в области математического ожидания ингредиента в многокомпонентной смеси содержания ингредиента при t = 0; X - коэффициент пропорциональности; О нс² - начальная дисперсия перераспределения частиц продукта в смеси (сегрегация), то из (6) при t = 0:

О с² = (1 - О с² )/ Х ,               (7)

а при t ^ да

X = (1 - О р² )/ О р² ,              (8)

Как правило [3, 4], при исследовании процессов смешивания используют разброс случайной величины, масштабированный через дисперсию о н2, который в случае двухкомпонентной смеси рассчитывается по соотношению

Он2 = с-(1 - с), где с – содержание ингредиента в смеси.

Тогда при t ^ 0 О н² = 1, О нс² = 0, а при t ^ да о ² = О с² = О р² .

После подстановки (5) в (6) получим:

1 d° = k [ 1 -^{( Л +} 0 °² 1 .

ПИ dl         Л

Л+Д

или

Методом разделения переменных имеем:

da ²         2 k4nl ,

,—г------------1 =------dl v2 [1 -(л+1). о2 ] Л

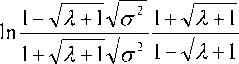
2 k nl

Л

t (12)

Подставив уравнение (7) в (12), получим:

ln

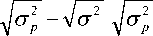
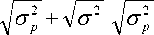
exp

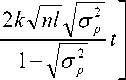
+ 1

- 1

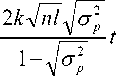
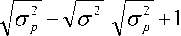
- 1

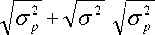
Таким образом, после преобразования уравнения (13) получаем математическую мо-

дель процесса смешивания в лопастном смеси теле в виде решения относительно о2:

г

г

• exp

—

^о = ^о р •

^{1 - о} р

• t

<

• exp

^{2 к}Д1 • рр 1            _________________________________________________________

—

1   /г2

^{1 - о} р

V

v

• t

v?

с начальными условиями t = 0; о² = 1; t = да ; о² = ор² .

Из полученного уравнения (14) следует, что процесс смешивания двухкомпонентной

смеси в лопастном смесителе определяется постоянной скорости смешивания k и предельной (равновесной) дисперсией содержания ингредиентов в смеси, то есть её однородностью.

Параметры k и О р² зависят от режима работы и конструктивных особенностей смесителя и определяются экспериментально.

Настройка параметров модели (14) осуществлялась по результатам экспериментальных исследований при смешивании измельчённого зерна пшеницы с металломагнитной примесью, которая являлась ключевым (индикаторным) компонентом.

По наилучшим оценкам константы постоянной скорости смешивания k и значениям равновесной дисперсии содержания ингредиентов σ р² проведена идентификация параметров математической модели (14).

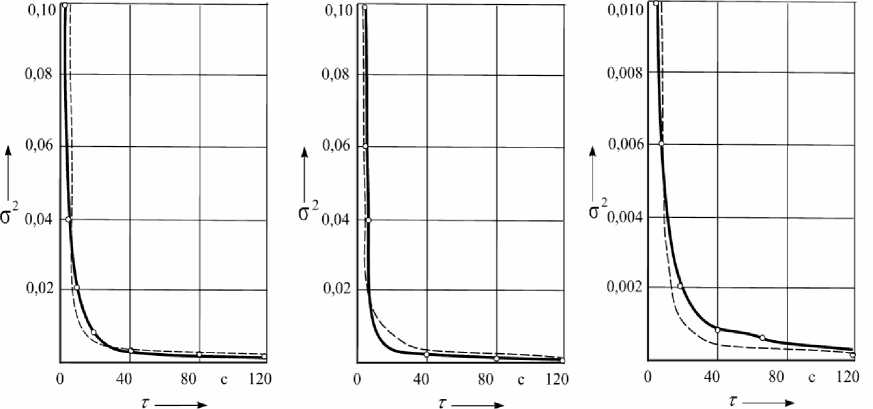
Результаты моделирования для рассматриваемых модельных смесей представлены на рисунке 2.

(a)                                       (b)                                          (с)

Рисунок 2. Кривые кинетики бинарных модельных смесей: (a) – измельчённое зерно пшеницы + металломагнитная примесь; (b) – измельчённое зерно пшеницы + соль поваренная; (c) – измельчённое зерно пшеницы + масло подсолнечное; экспериментальные ( ) и расчётные ( _ _ _ )

Figure 2. Model binary mixtures kinetics curves: (a) – milled grain of wheat + metallomagnetic mixture; (b) – shredded wheat grain + salt; (c) – shredded wheat + sunflower oil; Experimental ( ), Calculated (_ _ _)

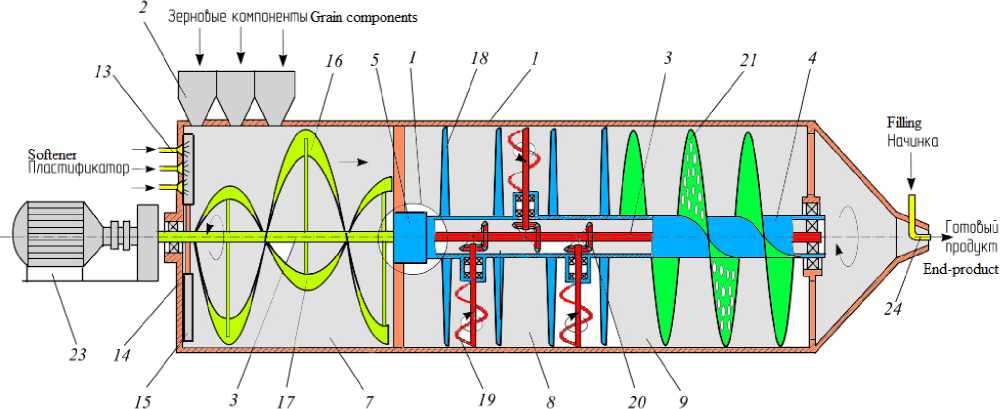
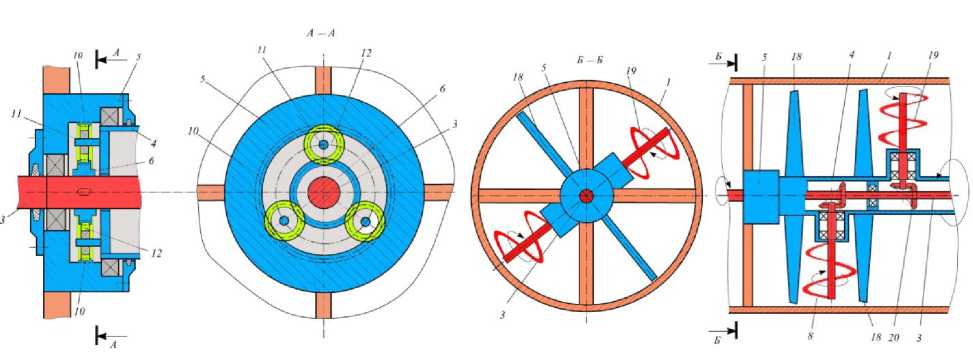
Полученные результаты использованы при разработке конструкция смесителя [5], особенность которого (рисунок 3) заключалась в том, что в первой камере на быстроходном валу после лопастей расположены две ленточные спирали разного диаметра с противоположной навивкой, обеспечивающие направление движения потоков смеси навстречу друг другу в виде перекрёстного противотока.

В предлагаемом смесителе за счёт конвективного, диффузионного смешивания, способствующих равномерному распределению частиц в смеси, и сегрегации, препятствующей этому процессу, можно регулировать интенсивность перемешивания многокомпонентной смеси посредством изменения угла поворота конусообразных лопастей и частоты вращения тихоходного и быстроходного валов.

(a)

(b)                                                                  (c)

Рисунок 3. Лопастной смеситель (a); продольные разрезы (b, c):1 – корпус; 2 – патрубки для загрузки ингредиентов; 3, 4 – быстроходный и тихоходный валы; 5 – опора; 6, 20 – зубчатые колёса; 7, 8, 9 – камеры; 10 – неподвижное колесо; 11 – водило; 12 – сателлит; 13 – форсунка; 14 – крышка; 15, 18 – лопасти; 16, 17, 19 – спирали; 21 – шнек; 22 – матрица; 23 – привод

Figure 3. A paddle mixer (a); longitudinal sections (b, c): 1 – body; 2 – pipes for ingredients loading; 3.4 – a high-speed and low-speed shafts; 5 – support; 6, 20 – gear; 7, 8, 9 – camera; 10 – stationary wheel; 11 – the carrier; 12 – satellite; 13 – nozzle; 14 – cover; 15, 18 – blades; 16, 17, 19 – helix; 21 – screw; 22 – matrix; 23 – drive

Конструкция предлагаемого смесителя позволит сократить продолжительность процесса смешивания, снизить удельные энергозатраты обеспечить высокую однородность многокомпонентной смеси; расширить область применения смесителя с учётом особенностей физико-механических характеристик смешиваемых ингредиентов.